Vierfeldertafel und Bayes - bonner

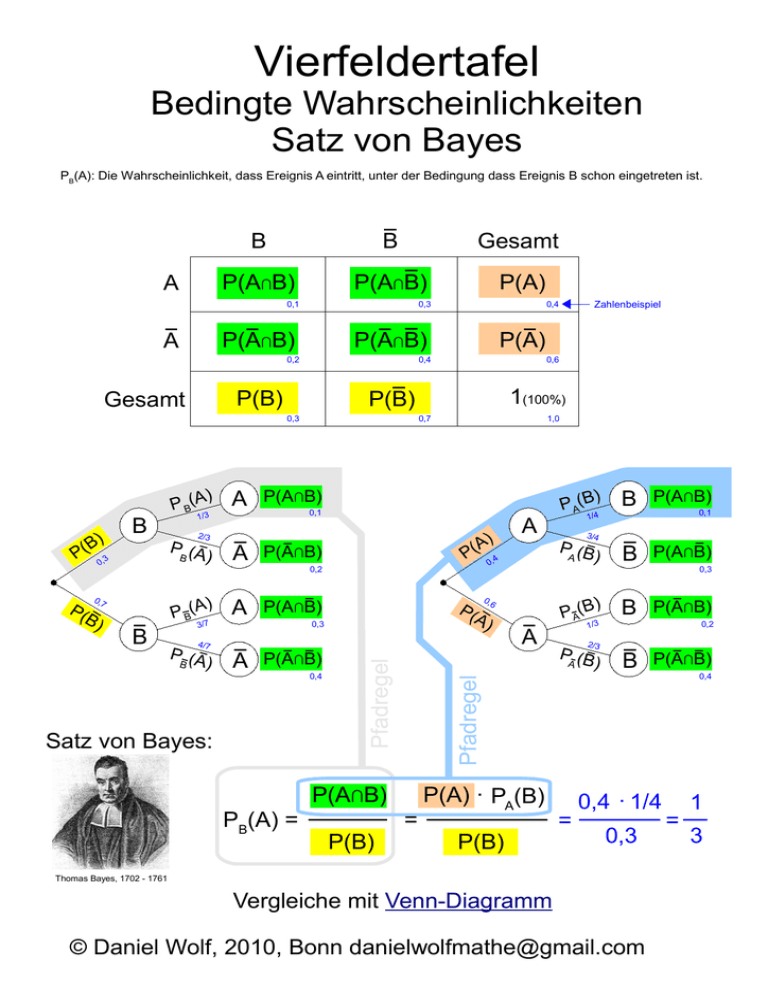
Vierfeldertafel
Bedingte Wahrscheinlichkeiten
Satz von Bayes
PB(A): Die Wahrscheinlichkeit, dass Ereignis A eintritt, unter der Bedingung dass Ereignis B schon eingetreten ist.
A
B
B
Gesamt
P(A∩B)
P(A∩B)
P(A)
0,1
0,3
P(A∩B)
A
P(A∩B)
0,2
0,7
B)
B
0,1
)
A
P(A∩B)
)
P B(A
A
P(A∩B)
0,2
3/7
4/7
P (A
B
)
A)
P( 0,4
P(
0,3
A
P(A∩B)
Satz von Bayes:
0,4
P(A∩B)
PB(A) =
P(B)
A
A
B
P(A∩B)
B
P(A∩B)
B
P(A∩B)
0,1
1/4
3/4
PA (B
)
)
PA(B
0,6
A)
)
PA(B
0,3
0,2
1/3
2/3
PA (B
)
B
P(A∩B)
0,4
Pfadregel
P(
2/3
1,0
P(A∩B)
1/3
PB (A
1(100%)
0,7
Pfadregel
B)
P( 0,3
B
A
0,6
P(B)
0,3
)
P B(A
P(A)
0,4
P(B)
Gesamt
Zahlenbeispiel
0,4
=
P(A) . PA(B)
P(B)
=
0,4 . 1/4
0,3
Thomas Bayes, 1702 - 1761
Vergleiche mit Venn-Diagramm
© Daniel Wolf, 2010, Bonn [email protected]
=
1
3