PowerPoint-Präsentation

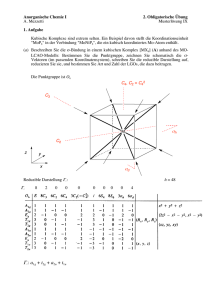
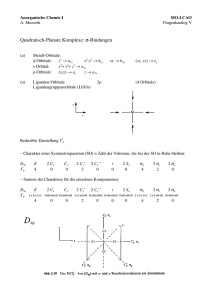
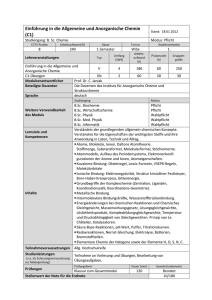
MO-Theorie von Komplexen
Ein Vortrag von Jasmin Fischer
1
Inhaltsübersicht
1. Elektronenzählregeln
2. Konstruktion eines MO-Schemas für
Komplexe
3. -Komplexe
4. -Komplexe
5. CO als Komplexligand
6. Zusammenfassung
7. Literatur
2
1. MOs in Komplexen
Metallorbitale
Molekülorbitale
Ligandenorbitale
N antibindende
9 Orbitale
9–N nichtbindende
N Orbitale
N bindende
„Anorganische Chemie“,Shriver, Atkins, Langford,VCH 1992, 1. Auflage S.227
3
1. MOs in Komplexen
Metallorbitale
Molekülorbitale
Ligandenorbitale
N antibindende
9 Orbitale
9–N nichtbindende
N Orbitale
N bindende
„Anorganische Chemie“,Shriver, Atkins, Langford,VCH 1992, 1. Auflage S.227
→ 18 – Valenzelektronen - Regel
4
18 – Valenzelektronen - Regel
Die intramolekulare Elektronenverteilung ist so vorzunehmen,
dass die Gesamtladung des
Komplexes erhalten bleibt:
2(C5H5-)
Fe2+
12 e6 e18 e-
2(C5H5•)
Fe0
Fe
10 e8 e18 e5
2. Konstruktion eines MO-Schemas
Allgemeine Vorgehensweise:
1. Bestimmung der Symmetrieklassen
der Metall-Orbitale
2. Ermittlung der entsprechenden
Ligandengruppenorbitale
3. Symmetrieadaptierte
Linearkombination der Orbitale
6
Charaktertafel Oh
Oh
E
8C3
6C2
6C4
3C2
i
6S4
8S6
3σh
6σd
A1g
1
1
1
1
1
1
1
1
1
1
A2g
1
1
-1
-1
1
1
-1
1
1
-1
Eg
2
-1
0
0
2
2
0
-1
2
0
T1g
3
0
-1
1
-1
3
1
0
-1
-1
T2g
3
0
1
-1
-1
3
-1
0
-1
1
A1u
1
1
1
1
1
-1
-1
-1
-1
-1
A2u
1
1
-1
-1
1
-1
1
-1
-1
1
Eu
2
-1
0
0
2
-2
0
1
-2
0
T1u
3
0
-1
1
-1
-3
-1
0
1
1
T2u
3
0
1
-1
-1
-3
1
0
1
-1
X2+y2+z2
(2z² - x² y², x²-y²)
(Rx, Ry, Rz)
(xz, yz, xy)
(x, y, z)
7
Charaktertafel Oh
korrelierende Metallorbitale
Oh
E
8C3
6C2
6C4
3C2
i
6S4
8S6
3σh
6σd
A1g
1
1
1
1
1
1
1
1
1
1
A2g
1
1
-1
-1
1
1
-1
1
1
-1
Eg
2
-1
0
0
2
2
0
-1
2
0
T1g
3
0
-1
1
-1
3
1
0
-1
-1
T2g
3
0
1
-1
-1
3
-1
0
-1
1
A1u
1
1
1
1
1
-1
-1
-1
-1
-1
A2u
1
1
-1
-1
1
-1
1
-1
-1
1
Eu
2
-1
0
0
2
-2
0
1
-2
0
T1u
3
0
-1
1
-1
-3
-1
0
1
1
T2u
3
0
1
-1
-1
-3
1
0
1
-1
X2+y2+z2
(2z² - x² y², x²-y²)
(Rx, Ry,Rz)
(xz, yz, xy)
(x, y, z)
8
2. Konstruktion eines MO-Schemas
Allgemeine Vorgehensweise:
1. Bestimmung der Symmetrieklassen
der Metall-Orbitale
2. Ermittlung der entsprechenden
Ligandengruppenorbitale
3. Symmetrieadaptierte
Linearkombination der Orbitale
9
Ligandengruppenorbitale
Ligandengruppenorbitale (LGO) müssen dieselbe
Symmetrie wie die Atomorbitale haben!
LGO (dz2) = N(+z+-z-+x--x-+y--y)
z
z
z
+
+
-+
-
-
 (xy)
-
y
+
x
+
z
++
 (xy)
y
y
y
+
++
x
x
x
pz
„Grundlagen der Komplexchemie“,Demuth, Kober,Otto Salle Verlag 1992, 2. Auflage S.110
pz
10
Symmetrienangepasste Orbitale Oh ()
z
A1g
y
s
x
Eg
y
z
x
y
dz²
x
T1u
z
d x² - y²
z
y
x
p
„Anorganische Chemie“,Shriver, Atkins, Langford,VCH 1992, 1. Auflage S.741
11
Symmetrienangepasste
Orbitale Oh ()
T1u
T2g
T1g
T2u
„Anorganische Chemie“,Shriver, Atkins, Langford,VCH 1992, 1. Auflage S.741
12
2. Konstruktion eines MO-Schemas
Allgemeine Vorgehensweise:
1. Bestimmung der Symmetrieklassen
der Metall-Orbitale
2. Ermittlung der entsprechenden
Ligandengruppenorbitale
3. Symmetrieadaptierte
Linearkombination der Orbitale
13
Bestimmung der Reihenfolge der
Energieniveaus in oktaedrischen
σ- Komplexen
1. s- und p-Orbitale überlappen stärker als d-Orbitale

die a1g und t1u sind die energieärmsten
MOs und die a1g* und t1u* die am höchsten
liegenden MOs
2. d -Orbitale überlappen nur schwach

die eg und eg*-Molekülorbitale werden
relativ zu ihrem Schwerpunkt wenig
verschoben
3. t2g-Orbitale sind nichtbindend und daher nicht
verschoben
14
Allgemeines
MO-Schema
für
σ-Komplexe
Komplexe, die diesem
Schema folgen sind
z.B.:
[Ti(H2O)6]3+,
[Co(NH3)6]3+
„Grundlagen der Komplexchemie“,Demuth, Kober,Otto Salle Verlag 1992, 2. Auflage S.110
15
Allgemeines Schema: MO-Diagramm für oktaedrische Komplexe
„Koordinationschemie“,Gade,WILEY-VCH 1998, 1. Auflage S.258
16
Der Einfluss der Liganden auf
die Ligandenfeldaufspaltung
-Akzeptor-Stärke nimmt zu
I- < Br- < S2- < SCN- < Cl- <NO3- < H2O < NH3 < en < CO
-Donor-Stärke nimmt zu
17
4. - Donor - Ligand
*
eg*
 Die voll besetzten 2pOrbitale der Liganden liegen
unter den 3d-Orbitalen des
Metall-Ions entsprechender
Symmetrie
e g*
10 Dq
10 Dq
*
t2g*
 Die Metall-Elektronen füllen
das t2g*-MO aus und erniedrigen
somit ΔO
t2g
T2g

besetzt
t2g
 - Komplex
 Die Elektronendichte hat sich
vom Liganden auf das
Zentralteilchen übertragen
 Orbitale der Liganden
„Anorganische Chemie“, Huheey,Walter de Gruyter 1988, 3. Auflage S.470
18
MO-Schema für
oktaedrische
Komplexe mit
-DonorLiganden
(I-, Cl-, F-, OH-)
„Grundlagen der Komplexchemie“,Demuth, Kober,Otto Salle Verlag 1992, 2. Auflage S.110
19
4. - Akzeptor-Liganden
*
t2g*
* e *
g
*
eg
leer
T2g
10 Dq
t2g
10 Dq

 -Komplex
t2g
 -Orbitale der
Liganden
 Die leeren 2p-Orbitale der
Liganden liegen über den 3dOrbitalen des Metall-Ions
entsprechender Symmetrie
 Die Metall-Elektronen füllen
das t2g-MO aus, welches aus
einem leeren -Orbital des
Liganden aufgebaut ist
 Die Elektronendichte hat sich
vom Zentralion auf den
Liganden übertragen
„Anorganische Chemie“, Huheey,Walter de Gruyter 1988, 3. Auflage S.471
20
- Hin- und - Rückbindung am
Beispiel von CO
-Hinbindung:
5 (CO) wirkt als e—
Donor mit einem
leeren Akzeptor-dOrbital.
- Rückbindung
Überlappung eines
besetzten d-Obitals
mit dem * des CO
„Koordinationschemie“,Gade,WILEY-VCH 1998, 1. Auflage S.104
21
Zusammenfassung
Bei der Konstruktion von MO-Schematas muss
beachtet werden:
• Die Symmetrie des Komplexes
• Die Symmetrie der Metallorbitale
• Die Symmetire der Ligandenorbitale
• Die Art der Liganden (π- und σ-Liganden)
Die Kombination der Orbitale erfolgt dann
nach dem selben Schema wie bei kleineren
Systemen.
22
Literatur
[1] „Organometallchemie“, Elschenbroich, Salzer,
B.G. Teubner, 1993, 3. Auflage
[2] „Anorganische Chemie“,Shriver, Atkins,
Langford,VCH 1992, 1. Auflage
[3] „Anorganische Chemie“, Huheey,Walter de
Gruyter 1988, 3. Auflage
[4] „Grundlagen der Komplexchemie“,Demuth,
Kober, Otto Salle Verlag 1992, 2. Auflage
[5] „Koordinationschemie“,Gade,WILEY-VCH 1998,
1. Auflage
[6] „Anorganische Chemie“, Riedel, de Gruyter 1999
23