Quadratisch-Planare Komplexe: σ

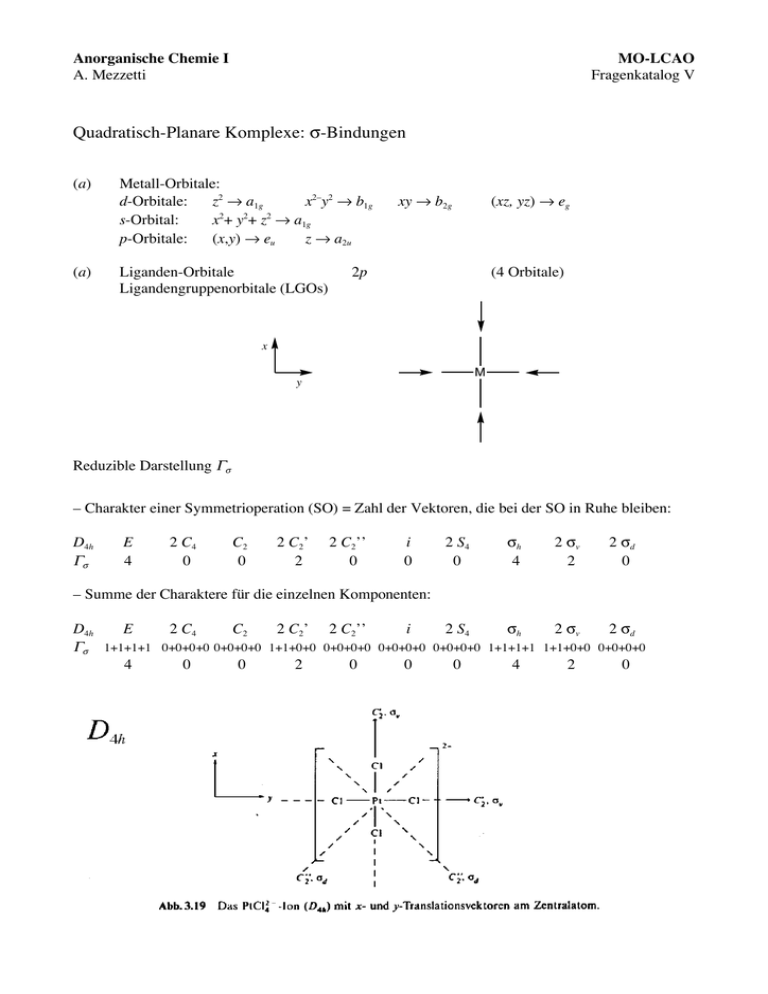
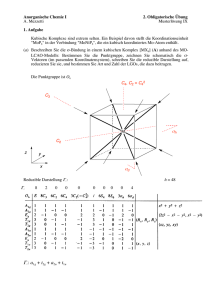
Anorganische Chemie I
A. Mezzetti
MO-LCAO
Fragenkatalog V
Quadratisch-Planare Komplexe: σ-Bindungen
(a)
Metall-Orbitale:
d-Orbitale:
z2 → a1g
x2–y2 → b1g
s-Orbital:
x2+ y2+ z2 → a1g
p-Orbitale:
(x,y) → eu
z → a2u
(a)
Liganden-Orbitale
Ligandengruppenorbitale (LGOs)
xy → b2g
(xz, yz) → eg
2p
(4 Orbitale)
x
M
y
Reduzible Darstellung Γσ
– Charakter einer Symmetrioperation (SO) = Zahl der Vektoren, die bei der SO in Ruhe bleiben:
D4h
Γσ
E
4
2 C4
0
C2
0
2 C2’
2
2 C2’’
0
i
0
2 S4
0
σh
4
2 σv
2
2 σd
0
– Summe der Charaktere für die einzelnen Komponenten:
D4h
E
2 C4
C2
2 C2’ 2 C2’’
i
2 S4
σh
2 σv
2 σd
Γσ 1+1+1+1 0+0+0+0 0+0+0+0 1+1+0+0 0+0+0+0 0+0+0+0 0+0+0+0 1+1+1+1 1+1+0+0 0+0+0+0
4
0
0
2
0
0
0
4
2
0
Reduktion
N = 1 # !rx "!ix "n x
h x
h = Gesamtzahl der Symmetrieoperationen in der PG = 16
n x = Anzahl von Operationen in der Klasse.
! rx = Charakter der Operation x in der reduziblen D.
! ix = Charakter der Operation x in der irreduziblen D.
Γσ
4
0
0
2
0
0
0
4
2
0
Γσ = a1g + b1g + eu
Die 4 LGOs bestehen aus
M
z
x
y
Metall-Orbitale: d(z2)
– 1 LGO mit a1g-Symmetrie
– 1 LGO mit b1g-Symmetrie
– 2 ent. LGOs mit eu-Symmetrie
M
M
M
M
x
a1g
b1g
s
d(x2–y2)
eu
y
(px , py)
Am Metall gibt es 2 Orbitale mit a1g-Symmetrie: s und d(z2). Beide Orbitale überlappen mit dem
a1g-LGO. Daraus entsthehen 3 Molekülorbitale. Zur Erinnerung: Die Bindung ist L→M-dativ.
Deshalb haben bindende Orbitale vorwiegend den Charakter der Ligandenorbitale und antibindende
Orbitale vorwiegend Metall-Charakter. Anders gesagt, durch die Bindung werden die Ligandenorbitale stabilisiert und die Metallorbitale destabilisiert. Somit:
– 1a1g ist stark bindend und vorwiegend auf den Liganden lokalisiert.
– 2a1g hat vorwiegend d(z2)-Charakter und ist schwach M–L-antibindend → seine Energie ist
höher als die von d(z2) im freien Metall.
– 3a1g hat vorwiegend s-Charakter und ist stark M–L-antibindend → seine Energie ist höher als die
von s im freien Metall.
Energieniveaudiagramm
Kommentare zum Energiediagramm:
Das einzige starl antibindende Orbital ist x2–y2 (wegen der vollständigen Überlappung mit dem
LGO mit b1g-Symmetrie).
d(z2) ist schwach antibindend, weil nur die Hälfte des Orbitals (die Komponente in der xy-Ebene)
mit den LGO's der Liganden überlappt. Die zweite z2-Hälfte liegt entlang der z-Achse und trägt
nicht zur Bindung bei.
Ein planar quadratischer d8-Komplex hat die Elektronenkonfiguration:
1b2g2 1eg4 2a1g2
Somit sind die energetisch hoch liegenden 2b1g -, 1a2u-, 3a1g- und 2eu-Orbitale vollständig unbesetzt!
(1a2u ist nicht bindend. alle andere sind antibindend). Deshalb bevorzugen low-spin d8-Komplexe
diese Geometrie. In einer oktaedrischen Geometrie hätte einen d8-Komplex die Elektronenkonfiguration t2g6 eg2 mit besetzten stark antibindenden eg-Orbitalen!
Die Reihenfolge der Energien der d-Orbitale ist nicht die gleiche wie in der KFT! Das HOMO ist
hier d(z2) und nicht d(xy). Dies hat damit zu tun, dass das Bild noch nicht vollständig ist. Es fehlen
die π-Bindungen (siehe Übung 7).