Document

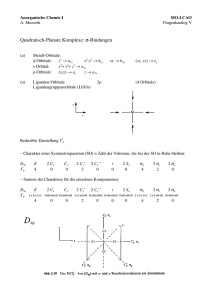
Anorganische Chemie I
A. Mezzetti
MO-LCAO
Fragenkatalog VIII
π-Bindungen in quadratisch-planaren Komplexen
–
–
Metall-Orbitale:
Liganden-Orbitale
???
2p
(? Orbitale)
(8 Orbitale)
Ligandengruppenorbitale (LGOs)
z
M
y
x
Wir haben vereinfacht angenommen, dass der Charakter einer Symmetrieoperation ist gleich der
Anzahl der Vektoren, die bei der SO in Ruhe gelassen werden. Diese Vereinfachung funktioniert
hier nicht: Wir müssen den Charakter für jeden Vektor ermitteln und alle Beiträge addieren, um den
Gesamtcharakter für eine Klasse von Symmetrieoperationen zu berechnen. Beispiel:
σh: (4 Vektoren in Ruhe → Beitrag ist +4) + (4 Vektoren um 180° rotiert→ Beitrag ist –4) = 0
Reduzible Darstellung Γπ
D4h
Γπ
E
8
2 C4
0
C2
0
2 C2’ 2 C2’’ i
–4
0
0
2 S4
0
σh
0
2 σv
0
Reduktion
N = 1 # !rx "!ix "n x
h x
ΓΠ
8
0
0
–4
0
0
0
0
h = Gesamtzahl der Symmetrieoperationen in der PG = 16
0
0
2 σd
0
Aus der Reduktion ergibt sich:
Γπ = a2g + b2g + eg + a2u + b2u + eu
Metall
k.O.
dxy
(dxz,dyz)
pz
k. O.
(px,py)
a2g und b2u sind strikt nichtbindend, weil das Metall keine Orbitale mit solcher Symmetrie besitzt.
Das Metall-a2u-Orbital (pz) überlappt sehr schwach mit dem LGO der gleichen Symmetrie und kann
als nicht bindend betrachtet werden. Dasselbe gilt für die eu-Orbitale. Somit sind nur die b2g- und egOrbitale relevant:
z
M
y
M
x
eg
dyz
M
dxz
b2g
a2u
M
*
dxy
pz
Die stärkste Wechselwirkung ergibt sich für die b2g-Orbitale, weil ein Metall-Orbital mit vier LGO's
überlappt (bei eg ein Metall-Orbital mit zwei LGO's). Demzufolge sind die Effekte auf die Energie
der b2g-Orbitale am grössten (siehe unten).
Wir müssen jetzt zwei Fälle unterscheiden:
1) Die 4 Liganden L besitzen energetisch tief liegende, besetzte π-Orbitale, sind also π-Donoren:
2b1g* "
"
1b2g* !
2a1g "
1eg* !
b2g
eg
b1g
eu
a1g
eg (!)
b2g (!)
1eg
1b2g
M
ML4
L4
Die π-Bindung ist dativ: Die Elektronen werden von den Liganden zum Metall transferiert. Deshalb
destabilisiert sie die Metallorbitale, vor allem das d(xy)-Orbital (b2g) (beste Überlappung, siehe
oben), welches π-antibindenden Charakter bekommt. Somit übersteigt seine Energie die vom
schwach σ-antibindenden d(z2)-Orbital (2a1g). Für die d8-Konfiguration heisst es, dass d(xy) das
HOMO des Komplexes ist.
N.B.: π-Donoren destabilisieren die d-Orbitale des Metalls mit π-Symmetrie (dπ). In der Regel
besitzen planar quadratische Komplexe die d8-Elektronenkonfiguration und die dπ-Orbitale des
Metalls sind vollständig besetzt. Deshalb ist zu erwarten, dass planar quadratische d8Komplexe mit
starken π-Donoren nicht besonders stabil sind!
2) 4 Liganden L mit energetisch hoch liegenden, unbesetzten π-Orbitalen (π-Akzeptoren):
1b2g*
1eg*
b2g (!)
eg (!)
2b1g* "
2a1g "
"
eg
b2g
1eg !
1b2g !
b1g
eu
a1g
M
ML4
L4
Die π-Bindung ist hier eine M→L-Rückbindung. Die Elektronen werden Metall zu unbesetzten
Ligandenorbitalen transferiert. Deshalb stabilisiert die π-Bindung die Metallorbitale, vor allem das
d(xy)-Orbital (b2g), welches π-bindenden Charakter hat. Somit ist seine Energie niedriger als die
vom schwach σ-antibindenden d(z2)-Orbital (2a1g). In der d8-Konfiguration ist nun das d(z2)-Orbital
das HOMO des Komplexes. Da es sterisch unbehindert ist (es liegt mehrheitlich ausserhalb der xyEbene), ist d(z2) für einen nukleophilen Angriff bestens geeignet (oxidative Addition, siehe Anorg.
Chem. 3)!
N.B.: π-Akzeptoren stabilisieren die vollständig besetzten d-Orbitale des Metalls mit π-Symmetrie
(dπ). Planar quadratische d8-Komplexe mit starken π-Akzeptoren sind besonders stabil und trotzdem
reaktiv als Nukleophile, weil die π-Rückbindung die Elektronendichte des HOMO nicht senkt
(siehe oben)!
(d) Vergleich der Resultate der MO-LCAO-Analyse für π-Donoren und π-Akzeptoren mit den
Voraussagen der Kristallfeld-Theorie für den gleichen Komplex:
Das KFT-Energieschema (siehe Skript) entspricht dem der π-Donoren, in dem die Energie des
d(z2)-Orbitals unterhalb der Energie des d(xy)-Orbitals liegt. Das MO-LCAO-Schema zeigt,
dasss dies nur für π-Donoren gilt. Hingegen stabilisieren π-Akzeptoren alle Orbitale mit πSymmetrie. Daher ist das d(z2)-Orbital das HOMO, mit den oben erwähnten Folgen.