1 Anorganische Chemie I Fragenkatalog V A. Mezzetti 1

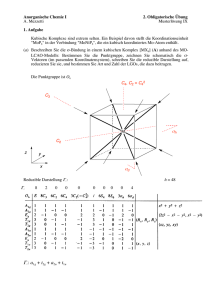
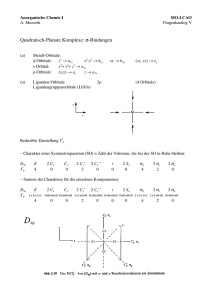
Anorganische Chemie I
A. Mezzetti
Fragenkatalog V
1. Obligatorische Übung
Aufgabe 1
Der farblose, diamagnetische Komplex trans-[Co(CO)3(PPh3)2]+ (A) ist trigonal bipyramidal.
(a) Bestimmen Sie Oxidationszahl, Elektronenkonfiguration, VE-Zahl und Punktgruppe von A!
(b) Entwickeln Sie ein KFT-Aufspaltungsmuster für A. Dabei sollen Sie zuerst anhand der
Symmetrie feststellen, in wie viele Sätze die d-Orbitale aufspalten, die Wechselwirkungen
zwischen den Liganden und dem Metall skizzieren, das Energieschema zeichnen, und die
Elektronen einfüllen. Hinweis: Verwenden Sie die oktaedrische Struktur (Oh-Punktgruppe) als
Ausgangspunkt und passen Sie sie an!
(a) [Co(CO)3(PPh3)2]+
d8
Co(I)
18 VE
D3h
(b) Die D3h-Charaktertafel zeigt, dass die d-Orbitale in drei Sätze aufspalten: a1', e' und e" (in der
D3h-Punkgruppe nimmt man die Richtung der C3-Achse als z-Achse):
Die M–L-Wechselwirkungen bestimmen die Reihenfolge der Energie der a1'-, e'- und e"-Sätze.
Mit einem oktaedrischen Komplex (Oh-Punktgruppe) als Ausgangspunkt erhält man:
Oh
z
L
x
M
L
–L
L
L
y
D3h
L
L
L
M
L
L
L
L
Die Entferung eines Liganden in der xy-Ebene entlastet das x2–y2-Orbital wesentlich. Der Effekt
wird durch die Drehung von zwei Liganden weg von der y-Achste verstärkt, wobei das xyOrbital destabilisiert wird:
xy
x
L
y
x2–y2
L
L
120 °
L
L
L
120 °
Aus der Skizze kann man schätzen, dass die Destabilisiert des xy-Orbitals durch Liganden
weniger als die Hälfte ist als die Destabilisierung im oktaedrischen Komplex. Erklärung: In A
werden nur zwei von vier Lappen des xy-Orbitals beansprucht (der dritte Ligand liegt auf einer
Knotenebene) und die entsprechenden Liganden befinden sich nicht auf der Achse des Orbitals,
wo die Elektronendichte am grössten ist. Im Gegensatz sind in einem oktaedrischen Komplex
vier Liganden direkt zum x2–y2-Orbital gerichtet.
1
Somit ist die Stabilisierung des x2–y2-Orbitals grösser als die Destabilisierung des xy-Orbitals.
Demzufolge liegt die Energie des entarteten e'-Satzes (xy und x2–y2) eher tief. Da die
Änderungen für z2- und (xz,yz) (e'') vergleichsmässig klein sind, kann man folgendes Energieschema entwerfen:
für d8:
D3h
Oh
a1'
a1'
e'
e'
e''
e''
(c) Die trigonale bipyramidale (TBP) Struktur eignet sich besonders gut für d8-Komplexe. Wieso?
D4h
D3h
Oh
x2–y2 (b1g)
a1'
eg
xy (b2g)
z2 (a1g)
e'
t2g
e''
(xz, yz) (eg)
Das erarbeitete Energieschema zeigt, dass in der trigonalen bipyramidalen Struktur 4 Orbitale
energetisch relativ tief liegen. Diese bieten Platz für die acht Elektronen der d8-Elektronen konfiguration ohne grossen Energieverlust. In der oktaedrischen Geometrie wären die eg-Orbitale
besetzt.
Die andere Struktur, die sich gut für d8-Komplexe eignet, ist die planar quadratische. Wie in der
Vorlesung diskutiert, hebt die Dissoziation der Liganden entlang der z-Achse die Entartung der
eg-Orbitale auf und senkt die Energie des z2-Orbitals. Der Gesamteffekt auf die Energie der
orbitale ist vergleichbar.
Aufgabe 2
Betrachten Sie den Komplex trans-[CrF2(en)2]+ (B).
(a) Bestimmen Sie Oxidationszahl, Elektronenkonfiguration, VE-Zahl und Punktgruppe von B.
trans-[CrF2(en)2]+
Cr(III)
d3
15 VE
D4h (ohne Chelatringe)
2
(b) In der Beschreibung der σ-Bindung in B (en = Ethylendiamin) anhand des MO-LCAO-Modells
werden die F- und N-Donoren getrennt behandelt, weil sie nicht äquivalent sind (es gibt keine
Symmetrieoperation, die die axialen und äquatorialen Donoren in einander überführt). Die
reduziblen Darstellungen für die N4- und F2-LGOs lauten:
N4
F2
z
M
y
M
x
Reduzible Darstellung Γ für die N4- und F2-Donoren:
σ
Γ (N4) 4
Γ (F2) 2
0
2
σ
σ
0
2
2
0
0
0
0
0
0
0
Γ (N)4: a1g + b1g + eu
4
0
2
2
0
2
Γ (F)2: a1g + a2u
σ
σ
Die LGOs sind (Die Position des Metalls ist mit "M" angedeutet):
N4
F2
M
M
M
M
M
M
a1g
a2u
z
x
eu
b1g
a1g
y
Die σ-antibindenden Orbitale (σ*) sind:
F2
M
N4
M
M
M
M
z
x
z
y
x
3a1g
x
y
2b1g
x
y
4a1g
y
M
2eu
a2u
3
(b) Stellen Sie das Energieniveauschema auf (mit Elektronen)!
(2 Punkte)
2eu
2a2u
4a1g
(s)
p
eu
a2u
s
a1g
d
b1g
a1g
b2g
eg
2b1g
3a1g
(z2)
b2g
eg
vollständig
besetzt
(12 e–)
b1g
eu
a1g
N4
a2u
a1g
F2
1b1g
1eu
1a2u
2a1g
1a1g
Qualitativ unterscheidet sich das Energieschema wenig von der Situation in der Oh-Symmetrie.
Die xy-, xz- und yz-Orbitale sind in beiden Fällen σ-nichtbindend. Die 3a1g- und 2b1g-Orbitale,
die hauptsächlich x2–y2- bzw. z2-Charakter besitzen, sind σ-antibindend (σ*). Vereinfachend
betrachten wir diese als Metallorbitale, obwohl sie eine (antibindende) Linearkombination
zwischen Metall- und Ligandenorbitalen sind.
Für die Bestimmung der relativen Energien der x2–y2- und z2-Orbitale ist die Betrachtung der
Feldstärke der Liganden hilfreich. Der Fluoroligand liegt tiefer in der spektroskopischen Reihe
als en. Somit ist die Ligandenfeldaufspaltung für F– kleiner ist als für en. Da die Ligandenfeldaufspaltung der Energiedifferenz zwischen t2g- und eg-Orbitalen (oder analogen) entspricht, darf
man davon ausgehen, dass das die Energie des 3a1g-Orbitals (hauptsächlich durch z2
beschrieben) in B niedriger ist, als die vom x2–y2-Orbital. Diese kleine Energiedifferenz spielt
aber keine Rolle, auch weil das Metallion nur drei Elektronen besitzt.
(c) Das magnetische Moment von B wird durch die Anzahl der ungepaarten Elektronen bestimmt.
Davon gibt es drei. Aus der Spin-only-Formel:
µ = 2 S(S +1) = n ( n + 2 ) = 3 (3+ 2 ) = 15 = 3.87 BM
4