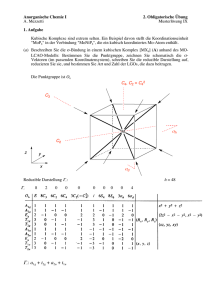
Spektren, Auswahlregeln und das Wigner-Eckart-Theorem

Universität Stuttgart
Institut für Theoretische und Angwandte Physik
Spektren, Auswahlregeln und
das Wigner-Eckart-Theorem
Hauptseminar: Gruppen in der Physik
Boris Lander
9. Januar 2008
Inhaltsverzeichnis
1 Einleitung
2
2 Grundlagen der Quantenmechanik
3
2.1 Was führte überhaupt zur Entwicklung der Quantenmechanik?
3
2.2 Quantenmechanische Postulate . . . . . . . . . . . . . . . . .
3
2.3 Schrödingergleichung . . . . . . . . . . . . . . . . . . . . . . .
5
2.4 Eigenwertspektrum & Quantenzahlen . . . . . . . . . . . . . .
6
2.5 Übergänge zwischen den Niveaus . . . . . . . . . . . . . . . .
7
2.5.1 Dipol-Übergänge . . . . . . . . . . . . . . . . . . . . .
8
2.5.2 Raman-Übergänge . . . . . . . . . . . . . . . . . . . .
9
2.6 Störungsrechnung . . . . . . . . . . . . . . . . . . . . . . . . . 11
2.6.1 Zeitunabhängige Störungsrechung . . . . . . . . . . . . 12
2.6.2 Zeitabhängige Störungsrechnung . . . . . . . . . . . . 14
3 Produkträume
17
4 Tensoroperatoren
20
4.1 Denition . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 20
4.2 Beispiel: Ortsoperator . . . . . . . . . . . . . . . . . . . . . . 21
5 Wigner-Eckart-Theorem
24
6 Physikalische Anwendungen des Wigner-Eckart-Theorems
27
6.1 Auswahlregeln . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6.1.1 Elektromagnetische Dipolübergänge . . . . . . . . . . 27
6.1.2 Ramanübergänge . . . . . . . . . . . . . . . . . . . . . 35
6.2 Eigenwertprobleme . . . . . . . . . . . . . . . . . . . . . . . . 37
7 Zusammenfassung
40
1
1
Einleitung
Eine, besonders in der Quantenphysik, sehr häug auftretende Problemstellung ist die Berechnung von sog. Matrixübergangselementen, deren Betragsquadrate im Wesentlichen die Wahrscheinlichkeit dafür beschreiben mit der
beispielsweise ein optischer Übergang eines Atoms stattndet. Ohne weitere Vereinfachung müssten hier sehr viele Matrixelemente berechnet werden.
Da diese Probleme jedoch sehr oft eine bestimmte Symmetrie aufweisen,
kann man unter deren Ausnutzung erhebliche Vereinfachungen erzielen. Und
genau hier setzt das Wigner-Eckart-Theorem an. Mit dessen Hilfe können
diese Symmetrien ausgenutzt werden um vorab schon Aussagen über das
Verschwinden, oder auch über die Verhältnisse der Intensitäten zwischen
verschiedenen Matrixübergangselementen zu machen. Aus dem Verschwinden solcher Matrixelemente können dann Auswahlregeln abgeleitet werden,
die besonders für die Spektroskopie von groÿer Bedeutung sind.
2
2
Grundlagen der Quantenmechanik
Um sich mit diesen Problemstellungen genauer auseinander setzen zu können
ist es zunächst nötig sich, zumindest in Grundzügen, mit den Ergebnissen
der Quantenmechanik vertraut zu machen.
2.1 Was führte überhaupt zur Entwicklung der Quantenmechanik?
Im Rahmen der klassischen Physik lassen sich einige Ergebnisse physikalischer Experimente nicht erklären. Beispiele hierfür sind:
• Die Diskretheit atomarer Spektrallinien
• Die Frequenzverteilung der Hohlraumstrahlung
• Die Wellennatur materieller Teilchen
All diese Probleme werden mit Hilfe der Quantenmechanik widerspruchsfrei
erklärbar.
Da die Ergebnisse der klassischen Mechanik in vielen Bereichen der Natur
jedoch durch Experimente sehr gut bestätigt wurden, müssen auch die Ergebnisse der Quantenphysik im klassischen Grenzfall ( im "Grenzfall groÿer
Quantenzahlen"bzw. ~ → 0), diese bereits verizierten Ergebnisse liefern.
Man bezeichnet dies als "Korrespondenzprinzip".
2.2 Quantenmechanische Postulate
Die grundlegenden Werkzeuge, die zum Verständnis der Quantenmechanik
nötig sind, sind die quantenmechanischen Postulate. Diese sollen Gegenstand
dieses Abschnitts sein.
Postulat 1 (Quantenmechanische Zustände) Der Quantenmechanische Zustand eines Teilchens wird durch eine komplexwertige Wellenfunktion
Ψ(r, t) beschrieben. Diese sind Elemente des Hilbertraums der quadratintegrablen Funktionen V über C, auf dem ein komplexes Skalarprodukt deniert
ist.
3
Postulat 2 (Superpositionsprinzip) Jede Linearkombination von quantenmechanischen Zuständen ist wieder ein möglicher quantenmechanischer
Zustand. Es gilt also das Superpositionsprinzip.
Postulat 3 (Kopenhagener Interpretation) Das Betragsquadrat einer
Wellenfunktion |Ψ(r, t)|2 ist als Wahrscheinlichkeitsdichte zu interpretieren.
D.h. |Ψ(r, t)|2 dV ist die Wahrscheinlichkeit dafür, das Teilchen zur Zeit t in
einem Volumenelement dV um r anzutreen.
Postulat 4 (Physikalische Observablen) Physikalische Observablen, also experimentell beobachtbare Gröÿen, werden in der Quantenmechanik durch
hermitesche Operatoren dargestellt. Die Messwerte sind die Eigenwerte des
zugehörigen Operators. (D.h. wenn sich ein quantenmechanisches System
nicht in einem Eigenzustand bendet, sondern in einer Linearkombination
aus solchen, so wird man es bei Messung einer Observablen immer in genau einem dieser Eigenzustände vornden. Man beeinusst also durch die
Messung das System, an dem man diese durchführt, selbst.)
Postulat 5 (Schrödingergleichung) Die zeitliche Entwicklung eines
quantenmechanischen Zustands wird durch die zeitabhängige Schrödingergleichung beschrieben.
ĤΨ(x, t) = i~
∂
Ψ(x, t)
∂t
Postulat 6 (Messwerte) Sei Ô ein hermitescher OperatorPmit den Eigenfunktionen ϕn (r) zu den Eigenwerten on . Und sei ϕ(r) = n cn ϕn (r) der
Zustand eines quantenmechanischen Systems. Dann ist |cn |2 die Wahrscheinlichkeit dafür, bei einer Messung der Observablen Ô an diesem System, den
Wert on zu messen. D.h. das System ist mit einer Wahrscheinlichkeit von
|cn |2 im Zustand ϕn (r) anzutreen.
4
2.3 Schrödingergleichung
Die zentrale Gleichung, mit der ein quantenmechanisches System beschrieben werden kann, ist die Schrödingergleichung. Diese lässt sich nicht streng
mathematisch herleiten und ist daher als Postulat zu verstehen (siehe oben).
Sie lautet:
ĤΨ(x, t) = i~
∂
Ψ(x, t)
∂t
(1)
In der Ortsdarstellung (x̂ = x, p̂ = −i~∇) hat der Hamiltonoperator die
Form:
Ĥ = −
~2
∆ + V (r, t)
2m
(2)
Damit lautet die Schrödingergleichung in der Ortsdarstellung:
−
~2
∂
∆ + V (r, t) Ψ(r, t) = i~ Ψ(r, t)
2m
∂t
(3)
h
Hier ist Ψ(x, t) die Wellenfunktion, Ĥ der Hamiltonoperator und ~ = 2π
mit dem Planckschen Wirkungsquantum h. Die Schrödingergleichung ist eine
lineare Dierentialgleichung (→ Superpositionsprinzip) zweiter Ordnung in
den Ortsvariablen und erster Ordnung in der Zeit.
Nimmt man nun an, dass der Hamiltonoperator zeitunabhängig ist, (wenn
also V (r, t) = V (r),) so ist für die Wellenfunktion ein Separationsansatz
folgender Form möglich:
Ψ(r, t) = ϕ(r)f (t)
(4)
Eingesetzt in die zeitabhängige Schrödingergleichung ergibt sich:
h
i
∂
Ĥϕ(r) f (t) = ϕ(r)i~ f (t)
∂t
(5)
Umgeformt erhält man:
i~ ∂ f (t)
Ĥϕ(r)
= ∂t
= Konstante = E
ϕ(r)
f (t)
5
(6)
Da die linke Seite der Gleichung nun nur noch vom Ort und die rechte nur
noch von der Zeit abhängt, die Gleichung aber für alle unabhängig voneinander gewählten r und t gelten muss, muss jede Seite der Gleichung für sich
konstant sein. Für die Zeitfunktion gilt dann:
i
f (t) = exp (− Et)
~
(7)
Der ortsabhängige Teil der Wellenfunktion muss dann die zeitunabhängige
Schrödingergleichung erfüllen:
Ĥϕ(r) = Eϕ(r)
(8)
Dies ist eine Eigenwertgleichung in der ϕ(r) die Eigenfunktionen und E die
Eigenwerte darstellen. E ist also der Eigenwert zum Hamiltonoperator. Dieser
beschreibt die Energie des quantenmechanischen Zustandes. Der Hamiltonoperator ist der, der Observable "Energie"zugeordnete, Operator.
Wie die Wellenfunktion physikalisch zu interpretieren ist, wurde bereits in
Postulat 3 beschrieben. Die Wellenfunktion ist im Allgemeinen eine komplexwertige Funktion. Da physikalisch messbare Gröÿen aber reell sein müssen,
hat die Wellenfunktion selbst also keine physikalische Bedeutung. Ihr Betragsquadrat jedoch sehrwohl. Dieses ist nach Postulat 3 physikalisch als
Aufenthaltswahrscheinlichkeitsdichte des beschriebenen Teilchens zu verstehen. Daraus folgt sofort die Normierungsbedingung:
Z
Ψ∗ ΨdV = 1
V
(9)
Denn die Wahrscheinlichkeit dafür, das Teilchen irgendwo im gesamten relevanten Volumen zu nden ist 1, da das Teilchen ja irgendwo sein muss.
Diese Normierungsbedingung muss als Randbedingung zusätzlich zur Schrödingergleichung erfüllt sein.
2.4 Eigenwertspektrum & Quantenzahlen
Die Schrödingergleichung ist für verschiedene einfache Potentiale exakt lösbar. Beispiele hierfür sind:
• Harmonisches Potential
• Kastenpotential
• Potentialbarriere
6
• Radialsymmetrisches Coulombpotential
Für gebundene/ungebundene Zustände ergibt sich in der Regel ein diskretes/kontinuierliches Eigenwertspektrum. D.h. im gebundenen Fall ist die Lösung der Schrödingergleichung nur für bestimmte, diskrete Energien möglich.
Jedem dieser Energiewerte kann man dann eine Zahl (→ Quantenzahl) zuordnen.
In der Quantenmechanik gilt folgender Satz:
Satz 1 (Kommutierende Operatoren) Zwei Observablen besitzen genau
dann einen vollständigen, gemeinsamen Satz orthonormaler Eigenfunktionen
(simultane Eigenfunktionen), wenn sie kommutieren.
Gibt es also Observablen, deren Operatoren miteinander kommutieren, so
kann man ein vollständiges, simultanes System von Eigenfunktionen wählen.
So gewählt sind diese Funktionen Eigenfunktion zu jeder dieser Observablen.
Wenn sich also ein System in einem solchen Eigenzustand bendet, kann man
all diese Observabeln messen, ohne das System zu beeinussen. Observablen
deren Operatoren vertauschen lassen sich also gleichzeitig beobachten.
Auÿerdem kann man dem System Quantenzahlen bezüglich jeder dieser Observablen zuordnen. Man nennt diese Quantenzahlen "gute Quantenzahlen".
Wird das System so gestört, dass die Operatoren nicht mehr vertauschen,
so gibt es keine simultanen Eigenfunktionen mehr und die Quantenzahlen
werden zu "schlechten Quantenzahlen".
Gibt man alle guten Quantenzahlen an, so ist die Wellenfunktion (bis auf
Phasenfaktoren) eindeutig bestimmt. Das heiÿt also, dass sich jeder quantenmechanische Zustand durch die Angabe aller guten Quantenzahlen charakterisieren lässt.
2.5 Übergänge zwischen den Niveaus
In einem quantenmechanischen System können nun Übergänge zwischen
den verschiedenen diskreten Energieniveaus stattnden. Dabei wird entweder Energie aufgenommen, dann geht das System in einen Zustand höherer
Energie über, oder es wird Energie abgegeben, dann geht das System in einen
Zustand niedrigerer Energie über. Im Folgenden sollen hier zwei spezielle Arten dieser Übergänge betrachtet werden.
7
2.5.1 Dipol-Übergänge
Bei Dipol-Übergängen handelt es sich um Übergänge, bei denen Photonen
absorbiert oder emittiert werden. Die Energie dieser Photonen (E = ~ω )
entspricht dabei genau der Energiedierenz der quantenmechanischen Zustände. Beobachtet man solche Übergänge bei Atomen, so liegen diese Energien gröÿenordnungsmäÿig häug im Bereich von wenigen eV, also im optisch
sichtbaren Bereich.
Man unterscheidet bei solchen Übergängen zwischen drei Fällen:
•
Absorption: Bei der Absorption trit ein Photon der Energie ~ω =
E2 − E1 auf das System, wird von diesem absorbiert und regt dabei
das System vom Zustand 1 mit der Energie E1 in den Zustand 2 mit
der Energie E2 an.
•
Induzierte Emission: Die induzierte Emission entspricht gerade dem
•
Spontane Emission: Die spontane Emission unterscheidet sich von
inversen Prozess der Absorption. Auch hier trit ein Photon der Energie ~ω = E2 − E1 auf das System, das sich jetzt aber in Zustand 2 bendet. Das Photon bewirkt nun den Übergang des Systems in Zustand
1 unter Emission eines Photons, das in Energie und Phase identisch zu
dem Photon ist, das den Übergang ausgelöst hat.
den beiden anderen Fällen. Nach einer gewissen mittleren Zeit geht ein
System, das sich in einem angeregten Zustand bendet, ohne äuÿeren
Einuss, in einen energetisch tiefer gelegenen Zustand über und sendet
dabei ein Photon der Energie ~ω = E2 − E1 aus, dessen Phase jedoch
zufällig ist.
8
Solche Übergänge sind nicht zwischen beliebigen Quantenzuständen möglich, sondern es gibt sogenannte Auswahlregeln, die verschiedene Übergänge
verbieten. Auÿerdem nden nicht alle Übergänge mit der gleichen Wahrscheinlichkeit statt. Wie man im Folgenden sehen wird, kann man mit Hilfe
des Wigner-Eckart-Theorems Aussagen über die Verhältnisse und das Verschwinden von Übergangswahrscheinlichkeiten treen.
2.5.2 Raman-Übergänge
Eine wichtige Methode zur Untersuchung von Molekülen ist die RamanSpektroskopie. Der Raman-Eekt beruht auf der inelastischen Streuung von
Licht an Molekülen. Inelastische Streuung bedeutet, dass bei der Streuung
Energie übertragen wird. Das also die Energie des gestreuten Photons verschieden von der Energie des einfallenden Photons ist. Dies macht sich in
der spektralen Verteilung des gestreuten Lichtes durch Linien bemerkbar,
deren Energie sich von der, der elastisch gestreuten Rayleigh-Linie unterscheidet. Diese Energieunterschiede hängen allein vom streuenden Molekül
und nicht von der Wellenlänge des einfallenden Lichts ab. Die Messung dieser
Energiedierenzen erlaubt es dann Rückschlüsse auf die Molekülstruktur zu
ziehen, denn diese Energiedierenzen entsprechen genau den Schwingungsund Rotationsenergien der streuenden Moleküle.
In der klassischen Optik erklärt man die elastische Streuung von Licht (Rayleigh-Streuung) dadurch, dass das elektrische Feld E des Lichtes an den
Hüllenelektronen des Moleküls angreift und dort ein Dipolmoment induziert
pind = αE. Dabei ist α die Polarisierbarkeit des Moleküls. Diese ist im
Allgemeinen anisotrop und kann muss daher durch einen Tensor zweiter Stufe
beschrieben werden. Dieses Dipolmoment schwingt dann mit der Frequenz
des Lichtes und emittiert deshalb selbst Dipolstrahlung mit der gleichen
Frequenz wie das anregende Licht.
Bei der Ramanstreuung unterscheidet man zwischen der Schwingungs- und
der Rotations-Raman-Streuung. Zuerst soll hier eine sehr anschauliche klassische Erklärung für den Raman-Eekt gegeben werden, die einige (aber
nicht alle) Beobachtungen gut erklärt. Danach soll die quantenmechanische
Erklärung noch angerissen werden.
Bei der Schwingungs-Raman-Streuung wird zunächst angenommen, dass
das Molekül nicht rotiert, sondern ausschlieÿlich schwingt. Bei der klassischen Erklärung geht man davon aus, dass das eingestrahlte Primärlicht der
Frequenz ωp im Molekül ein Dipolmoment pind = αE induziert. Da jedoch
die Polarisierbarkeit in der Regel von den Bindungslängen abhängt, wird
dieses durch eine Schwingung mit der Schwingungsfrequenz ωvib periodisch
verändert. Durch die zeitlich veränderliche Polarisierbarkeit wird nun das
Dipolmoment, welches mit der Frequenz des Primärlichtes schwingt, durch
9
die Schwingungsfrequenz des Moleküls moduliert. Für das Beispiel eines linearen zweiatomigen Moleküls mit Bindungslänge R gilt in erster Ordnung
für die Polarisierbarkeit längs der Schwingungsachse:
α(R) = α(R0 ) +
dα
(R − R0 ) + . . .
dR
(10)
Damit erhält man für das induzierte Dipolmoment:
pind (t) = α(t)E0 cos(ωp t) =
α(R0 ) +
dα
(R − R0 ) E0 cos(ωp t)
dR
(11)
Für die Molekülschwingung gilt:
R − R0 = a cos(ωvib t)
(12)
Eingesetzt und umgeformt erhält man:
p(t) = α(R0 )E0 cos(ωt) +
1 dα
E0 a (cos((ωp + ωvib )t) + cos((ωp − ωvib )t))
2 dR
(13)
Man erkennt also neben dem Term, der mit der Primärfrequenz schwingt,
zwei weitere Terme, die mit den um ωvib verschobenen Frequenzen ωp ± ωvib
schwingen. Dabei bezeichet man die zu niedrigeren Frequenzen vorschobene Linie als Stokes-Linie, die zu höheren Frequenzen verschobene als AntiStokes-Linie. Berücksichtigt man in der Reihenentwicklung noch weitere Terme, so ergeben sich noch weitere Schwingungen der Frequenz ωp ± 2ωvib ,
ωp ± 3ωvib , . . . Die Intensitäten nehmen jedoch mit zunehmender Ordnung
ab. Der Schwingungs-Raman-Eekt tritt nicht auf, wenn die Polarisierbarkeit nicht von den Bindungslängen abhängt. Für den Fall des zweiatomigen
dα
Moleküls bedeutet dies in erster Ordnung dR
= 0.
Zwar liefert die klassische Theorie eine sehr anschauliche Erklärung des Effekts, wenn man sich jedoch für die Intensitäten der verschiedenen Linien
interessiert, liefert die Theorie falsche Ergebnisse. Denn nach der klassischen
Theorie müssten die Stokes- und die Anti-Stokes-Linie die gleiche Intensität
haben. Dies ist jedoch, besonders für niedrige Temperaturen, nicht der Fall.
Die Anti-Stokes-Linie hat eine höhere Energie als die Unverschobene, daher
muss die Energie vom Moleküle abgegeben werden können. Dies ist nur der
Fall, wenn sich das Molekül bereits in einem angeregten Zustand bendet.
Da jedoch im thermischen Gleichgewicht die Wahrscheinlichkeit dafür, dass
sich das Molekül in einem angeregten Zustand bendet immer kleiner ist als
die, dass es sich im Grundzustand bendet, muss die Intensität der StokesLinie gröÿer sein als die der Anti-Stokes-Linie. Für groÿe Temperaturen wird
der Unterschied jedoch immer kleiner.
Bei der Rotations-Raman-Streuung beobachtet man zur Primärfrequenz
verschobene Linien, deren Energieunterschied zur Primärlinie hier jedoch
10
Rotationsquanten entsprechen. Auch hier liefert ein klassisches Modell eine
anschauliche Erklärung, mit der sich der Eekt zumindest in den Grundzügen
verstehen lässt. Da die Polarisierbarkeit eines nicht-rotationssymmetrischen
Moleküls anisotrop ist, muss man diese als Tensor zweiter Stufe behandeln.
Nun sollen die beiden Haupt-Polarisierbarkeiten mit α⊥ und αk bezeichnet
werden. Dabei stehen αk und α⊥ für die lange und die kurze Achse des symmetrischen Polarisierbarkeitstensors. Meistens weist dabei αk in Richtung
der Figurenachse des Moleküls und α⊥ in eine Richtung senkrecht dazu.
Wenn nun das Molekül rotiert, verändert sich also die Polarisierbarkeit mit
der doppelten Rotationsfrequenz des Moleküls. → Die doppelte Frequenz, da
die Polarisierbarkeit schon nach einer halben Umdrehung wieder die gleiche
Polarisierbarkeit vorliegt wie am Anfang. Auch hier wird durch die veränderliche Polarisierbarkeit das induzierte Dipolmoment noch zusätzlich moduliert. Analog zum Schwingungs-Raman-Eekt treten im Frequenzspektrum
zusätzlich zur unverschobenen Linie noch um die doppelte Rotationsfrequenz
zu höheren und zu tieferen Frequenzen verschobene Linien auf.
Der Rotations-Raman-Eekt tritt nur auf, wenn α⊥ 6= αk . Da die Rotationsenergien niedriger liegen als die Schwingungsenergien, sind die Verschiebungen kleiner als die beim Schwingungs-Raman-Eekt. Aus dem selben
Grund sind bei Normaltemperatur auch höhere Zustände angeregt, daher ist
der Intensitätsunterschied zwischen den Stokes- und den Anti-Stokes-Linien
wesentlich kleiner als beim Schwingungs-Raman-Eekt.
Ähnlich den Dipolübergängen sind auch bei den Ramanübergängen nicht alle
Übergänge erlaubt. Es gibt also auch hier Auswahlregeln, die sich im Fehlen
bestimmter Linien im Spektrum ausdrücken.
Die quantenmechanische Erklärung soll hier nur angerissen werden. Hier
stellt man sich den Vorgang folgendermaÿen vor (vgl. Abbildung 1): Ein
quantemechanisches System bendet sich im Zustand E 0 , durch Absorption eines Photons der Energie E wird es in ein sehr kurzlebiges, virtuelles
Energieniveau Evirtuell angehoben. (Für sehr kurze Zeit ist ein solches virtuelles Energieniveau gemäÿ der Energie-Zeit-Unschärferelation denkbar.) Von
dort geht das System unter Emission eines Photons in einen Zustand der
Energie E 00 über. Das ausgesandte Photon hat die Energie E − (E 00 − E 0 ).
Dieser Prozess wird Stokes-Prozess genannt. Den umgekehrten Prozess E 00 →
Evirtuell → E 0 nennt man Anti-Stokes-Prozess. Durch die von der Temperatur abhängigen Besetzungszahlen lassen sich nun auch die unterschiedlichen
Intensitäten von Stokes- und Anti-Stokes-Linien erklären.
2.6 Störungsrechnung
Da die Schrödingergleichung nur in wenigen einfachen Fällen exakt lösbar
ist, bedient man sich verschiedener Näherungsverfahren. Eines davon ist die
11
Abbildung 1: Ramaneekt
Störungsrechnung. Sie ist nur dann anwendbar, wenn man sich den Hamiltonoperator eines Systems als Summe eines Hamiltonoperators, für den die
Lösung der Schrödingergleichung bereits bekannt ist und einem Störoperator, dessen Auswirkungen im Vergleich zum anderen Summanden nur sehr
klein sind, denken kann. Wie das genau zu verstehen ist wird im Folgenden
geklärt. Man unterscheidet zwei wichtige Fälle: Die zeitunabhängige und die
zeitabhängige Störungsrechnung.
2.6.1 Zeitunabhängige Störungsrechung
1. Nicht-entarteter Ausgangszustand :
Wir wollen nun ein System mit dem Hamilton-Operator
(14)
H(λ) = H0 + Ṽ
betrachten. Dabei nehmen wir an, dass die Eigenfunktionen und Eigenwerte zum Operator H0 bekannt sind. Weiter nehmen wir an, dass
sich Ṽ durch λV ausdrücken lässt, wobei λ eine dimensionslose sehr
kleine reelle Zahl ist und die charakteristischen Energien von V und
H0 vergleichbar sind. Es soll also Folgendes gelten:
H = H0 + λV
mit
λ1
(15)
Weiterhin soll angenommen werden, dass das Eigenwertspektrum von
H0 diskret ist und die Eigenzustände einen vollständigen orthonormierten Satz von Eigenfunktionen bilden. Also:
sowie
H0 ϕip = Ep0 ϕip
(16)
X ϕip ϕip = id
(17)
p,i
und
i j
ϕp ϕq = δi,j δp,q
12
(18)
Dabei gibt p an, zu welchem Eigenwert ϕip gehört und i ist der Entartungsindex, mit i = 1, . . . , gp , wenn gp der Entartungsgrad des Energieniveaus p ist.
Es gilt also:
H(λ) |Ψ(λ)i = E(λ) |Ψ(λ)i
(19)
wobei |Ψ(λ)i der Eigenzustand und E(λ) der Energieeigenwert zum
gestörten Hamiltonoperator sind.
Weiterhin wird angenommen, dass sowohl die Energieeigenwerte, als
auch die Eigenfunktionen in Potenzen, von λ entwickelt werden können.
E(λ) =
X
(20)
λi i
i
und
|Ψ(λ)i =
X
(21)
λi |ii
i
Setzt man all dies in die Schrödingergleichung ein und vergleicht sukzessive Terme nullter, erster, zweiter, etc. Ordnung in λ, so ergibt sich
in a-ter Ordnung:
(H0 − 0 ) |ai + (V − 1 ) |a − 1i −
a
X
j |a − ji = 0
(22)
j=2
Fordert man zusätzlich, dass die Wellenfunktion gemäÿ
(23)
hΨ(λ) |Ψ(λ)i = 1
normiert ist, so kann man die Korrekturen in a-ter Ordnung berechnen.
Für die Energie-Korrekturen ergibt sich:
nullte Ordnung 0 = Ep0
erste Ordung
1
= h0| V |0i
zweite Ordung
2
=
2
|hϕip |V |ϕn i|
P
p6=n,i
0 −E 0
En
p
2. Entarteter Ausgangszustand :
Im entarteten Fall soll uns nun die Betrachtung der Energiekorrektur
in erster Ordnung genügen. Die Betrachtung erfolgt analog zum nichtentarteten Fall.
Der Grundzustand sei gegeben durch:
|0i =
gn
X
i=1
13
ci ϕin
(24)
wobei gn der Entartungsgrad ist.
Führen wir jetzt einen Operator P0 ein, der einen beliebigen Zustand
in den Entartungsraum zur Energie n projiziert:
P0 =
gn
X
i i ϕn ϕn (25)
i=1
Analog zum nicht-entarteten Fall erhält man in nullter und erster Ordnung in λ:
H0 |0i = En0 |0i
(26)
und
(H0 − En0 ) |1i + (V − 1 ) |0i = 0
(27)
Wendet man P0 auf Gleichung (27) an, so erhält man eine Eigenwertgleichung mit der sich die Energiekorrekturen bestimmen lassen. Formt
man diese Gleichung dann noch unter Verwendung von
P0 |0i = |0i
(28)
und Gleichung (18) um, so erhält man:
gn
X
ϕin V ϕjn cj = i ci
(29)
j=1
Dies ist eine Eigenwertgleichung. Besitzt diese nicht gn gleiche Eigenwerte, so ergeben sich unterschiedliche Energiekorrekturen. D.h. die
Zustände für die sich unterschiedliche Korrekturen ergeben sind nach
hinzufügen der Störung nicht mehr entartet, sie spalten also auf. Je
nach Symmetrie der Störung besteht auch die Möglichkeit, dass das
Energienieveau auch teilweise oder gar nicht aufspaltet. Mit Hilfe des
Wigner-Eckart-Theorems lässt sich dies (bis auf spezielle Ausnahmen)
vorhersagen, ohne zuvor das Eigenwertproblem explizit zu lösen.
2.6.2 Zeitabhängige Störungsrechnung
Da wir uns im Folgenden insbesondere für Übergangswahrscheinlichkeiten
zwischen diskreten Quantenzuständen interessieren, sollten wir uns zunächst
damit befassen, wie man diese berechnet. Dazu bedienen wir uns der zeitabhängigen Störungsrechung.
Wir betrachten ein nicht-entartetes, diskretes System von Quantenzuständen. Auch hier seien wieder die Eigenfunktionen und Eigenwerte des ungestörten Systems bekannt.
H0 |ϕn i = En |ϕn i
14
(30)
Analog zum vorherigen Abschnitt fügen wir dem Hamiltonoperator eine nun
zeitabhängige Störung Ṽ (t) = λV (t) hinzu. Es soll gelten:
H(t) = H0 + λV (t)
mit
λ1
(31)
Die zeitabhängige Störung soll zum Zeitpunkt t0 einsetzen. D.h. V (t < t0 ) =
0. Als Anfangsbedingung nimmt man an, dass sich das System zum Zeitpunkt
t0 im Eigenzustand |ϕi i des ungestörten Systems bendet.
(32)
|Ψ(t = t0 )i = |ϕi i
Gemäÿ Postulat 6 ist die Wahrscheinlichkeit dafür, das System zum Zeitpunkt t im Zustand |ϕf i zu nden, gegeben durch:
(33)
Pf i (t) = |hϕf |Ψ(t)i|2
Unter unserer Anfangsbedingung ist dies genau die Wahrscheinlichkeit dafür,
dass bis zum Zeitpunkt t der Übergang |ϕi i −→ |ϕf i stattgefunden hat.
Diese Wahrscheinlichkeit wollen wir jetzt berechnen.
Dazu entwickeln wir |Ψ(t)i nach dem zeitunabhängigen, vollständigen System von Eigenfunktionen des ungestörten Hamiltonoperators. Die Zeitabhängigkeit der Funktion ist daher nur in den Entwicklungskoezienten zu
nden.
X
|Ψ(t)i =
cn (t) |ϕn i
(34)
n
Des Weiteren wissen wir, dass die Zeitentwicklung der Eigenzustände eines
zeitunabhängigen Hamiltonoperators folgende Form hat:
|Φ(t)i = e−i
En
t
~
(35)
|ϕn i
Wenn wir also die Koezienten cn (t) durch cn (t) = e−i ~ t bn (t) ersetzen, so
können wir bei einer kleinen Störung annehmen, dass sich die bn (t), zumindest für kurze Zeiten, nur sehr wenig ändern.
En
Setzt man die Entwicklung von |Ψ(t)i mit den Koezienten bn (t) und dem
gestörten Hamiltonoperator in die zeitabhängige Schrödingergleichung ein
und wendet von links hϕn | darauf an, so erhält man:
i~
wobei ωmn =
X
d
bn (t) = λ
eiωmn hϕn | V (t) |ϕm i bm (t)
dt
m
Em −En
~
(36)
die Bohrfrequenz ist.
Bis hier wurde noch nicht davon Gebrauch gemacht, dass die Störung klein
ist. Diese Gleichung hier ist also noch äquivalent zur zeitabhängigen Schrödingergleichung. Nun wollen wir aber verwenden, dass sich die Koezienten
15
bn (t) nur langsam ändern. Ist dies der Fall, so lassen sich diese, für kurze
Zeiten, in eine Potenzreihe in λ entwickeln:
(1)
(2)
2
bn (t) = b(0)
(37)
n (t) + bn (t)λ + bn (t)λ + . . .
Setzt man diese Entwicklung ein, so erhält man in nullter Ordnung in λ:
i~
d (0)
b (t) = 0
dt n
(38)
Mit der Anfangsbedingung folgt daraus:
(39)
b(0)
n (t) = δni
In erster Ordnung ergibt sich dann:
i~
X
d (1)
bn (t) =
eiωnm t hϕn | V (t) |ϕm i b(0)
m (t)
dt
m
(40)
Verwendet man b(0)
m (t) = δmi und integriert die Gleichung von t0 , was o.B.d.A
gleich Null gesetzt werden kann, bis t, so ergibt sich:
b(1)
n (t)
1
=
i~
Z
t
(41)
eiωni t̃ hϕn | V (t̃) |ϕi idt̃
0
2
Für die Übergangswahrscheinlichkeit Pif (t) = |hϕf |Ψ(t)i|2 = λ2 b(1)
f (t)
ergibt sich damit:
2
Z
λ2 t iωf i t̃
hϕf | V (t̃) |ϕi idt̃
Pif (t) = 2 e
~
0
(42)
Im Falle einer sinusförmigen Störung, wie man sie bei der Absorption oder
der stimulierten Emission von Photonen annehmen kann, ergibt sich:
|hϕf | V |ϕi i|2
Pif (t) =
4~2
ei(ωf i +ω)t − 1 ei(ωf i −ω)t − 1 2
−
ωf i + ω
ωf i − ω (43)
Im Resonanzfall, also für ω → ±ωf i , kann man jeweils den einen Summanden zwischen den Betragsstrichen gegenüber dem Anderen vernachlässigen,
dessen Nenner gegen Null geht1 . Es ergibt sich dann:
|hϕf | V |ϕi i|2 2 sin(ωf i t/2) 2
Pif (t) =
t ~2
ωf i t/2 (44)
Wie man hier sehr gut erkennen kann, ist die Übergangswahrscheinlichkeit
zwischen zwei quantenmechanischen Zuständen proportional zum Betragsquadrat von hϕf | V |ϕi i. Dies bezeichnet man als Übergangsmatrixelement.
Insbesondere wird die Übergangswahrscheinlichkeit Null, wenn das Übergangsmatrixelement verschwindet.
1
Eine Begründung hierfür ist in Lehrbüchern der Quantenmechanik gegeben.
16
3
Produkträume
Besonders in der Quantenphysik hat man sehr häug mit Produkträumen
zu tun. Beispielsweise setzt sich die Gesamtwellenfunktions eines Teilchens
im Allgemeinen aus einer Funktion aus dem Ortsraum und einer Funktion
aus dem Spinraum zusammen. Das gesamte System lässt sich dann in dem,
durch das direkte Produkt von Orts- und Spinraum aufgespannten Raum,
beschreiben. Diesen Produktraum kann man bezüglich der Darstellung einer
Gruppe, über diesem Produktraum, in invariante Unterräume zerlegen. Wie
dies umgesetzt wird, soll in diesem Abschnitt behandelt werden.
Denition 1 (Direktes Produkt von Vektorräumen) Seien V und W
Vektorräume mit den Basen {v1 , . . . , vn } sowie {w1 , . . . , wm }, dann bezeichnet man den, von allen direkten Produkten der Basisvektoren von V mit den
Basisvektoren von W aufgespannten Vektorraum, als das direkte Produkt der
Vektorräume V und W.
V ⊗ W = hvi ⊗ wj |i = 1, . . . , n; j = 1, . . . , mi
Dies lässt sich ohne Weiteres auf das direkte Produkt von q Vektorräumen
miteinander verallgemeinern.
In der Darstellungstheorie lässt sich auÿerdem folgender Satz zeigen:
Satz 2 (Satz zur Produktdarstellung) Seien D(α) : G → GL(V ) bzw.
D(β) : G → GL(W ) unitäre, irreduzible Darstellungen der Gruppe G
(α)
über dem Vektorraum V bzw. W mit den Basen {v(α)
1 , . . . , vdα } bzw.
(β)
(β)
{u1 , . . . , udβ }, so ist die Produktdarstellung
Def.
D(α×β) = D(α) ⊗ D(β) : G → GL(V ⊗ W )
eine im Allgemeinen reduzible Darstellung über dem Produktraum von V und
W. Auch dieser Satz lässt sich auf das Produkt von q unitären, irreduziblen
Darstellungen verallgemeinern.
Doch wie ergeben sich nun die Matrixelemente der Produktdarstellung aus
denen der Darstellungen D(α) und D(β) ?
17
Dazu betrachten das Transformationsverhalten eines beliebigen Vektors x
aus V ⊗ W unter der Wirkung eines Gruppenelements g:
x̄ =
D(α) (g) ⊗ D(β) (g)
x=
X
D(α) (g) ⊗ D(β) (g) xij (vi ⊗ wj ) (45)
i,j
Die Darstellungen wirken jeweils nur auf den Teil des Basisvektors, der aus
dem zur jeweiligen Darstellung gehörenden Vektorraum stammt.
x̄ =
X
X
(α)
(β)
xij D(α) (g)vi ⊗ D(β) (g)wj =
xij Dki (g)vk ⊗ Dlj (g)wl
i,j
i,j,k,l
(46)
damit erhält man dann:
x̄ =
XX
k,l
(α)
(β)
Dki (g)Dlj (g) xij (vk ⊗ wl )
(47)
i,j
|
{z
}
x̄kl
Das heiÿt die Komponenten eines beliebigen Vektors aus dem Produktraum
transformieren sich wie folgt:
x̄kl =
X
X (α×β)
(α)
(β)
Dki (g)Dlj (g) xij =
Dkl,ij (g)xij
ij
(48)
ij
Man erhält also die Komponenten:
(α×β)
(α)
(49)
(β)
Dkl,ij (g) = Dki (g)Dlj (g)
Die Charaktere erhält man durch Spurbildung:
χ(α×β) (g) =
X
(α×β)
Dij,ij (g) =
i,j
X
(α)
(β)
Dii (g)Djj (g)
(50)
i,j
Die Summe lässt sich in zwei Faktoren zerlegen:
χ(α×β) (g) =
(
X
i
Es ergibt sich also:

) 
X

(α)
(β)
Dii (g) ·
Djj (g) = χ(α) (g)χ(β) (g)


(51)
j
χ(α×β) (g) = χ(α) (g)χ(β) (g)
(52)
Die Charaktere der Produktdarstellung ergeben sich also als Produkt der
Charaktere der einzelnen Darstellungen. Mit deren Hilfe lässt sich diese Produktdarstellung leicht in irreduzible Darstellungen zerlegen. Es gilt:
D(α) ⊗ D(β) =
M
γ
18
(αβ|γ)D(γ)
(53)
Dabei sind die Reduktionskoezienten
(αβ|γ) =
1 X (α)∗
χ
(g)χ(β)∗ (g)χ(γ) (g)
|G|
(54)
g∈G
die Multiplizitäten der irreduziblen Darstellungen in der Produktdarstellung.
Um jetzt die Basisvektoren einer ausreduzierten (orthonormalen) Basis durch
die Basisvektoren des Produktraumes auszudrücken, muss man einen Basiswechsel durchführen.
γ)
=
u(γ,s
k
X
(β)
v(α)
⊗ wj hαiβj |γsγ ki
i
(55)
|αii ⊗ |βji hαiβj |γsγ ki
(56)
γ)
u(γ,s
hγsγ k |αiβji
k
(57)
α,i,β,j
Oder in Bra-Ket-Notation:
|γsγ ki =
X
α,i,β,j
Für die Rücktransformation gilt:
(β)
v(α)
⊗ wj =
i
X
γ,sγ ,k
In Bra-Ket-Notation:
|α, ii ⊗ |β, ji =
X
|γ, sγ i hγsγ k |αiβji
(58)
γ,sγ ,k
Dabei sind hαiβj |γsγ ki die Clebsch-Gordan-Koezienten (oder auch Kopplungskoezienten).
Nebenbemerkung: Ermittlung der Clebsch-Gordan-Koezienten
Mit Hilfe von Projektionsoperatoren (siehe Vortrag über Molekülschwingungen) lassen
sich die invarianten Unterräume zu einer Darstellung nden. Wählt man in diesen invarianten Unterräumen, in standardisierter Art und Weise, (orthonormale) Basen, so sind
die Koezienten in der Linearkombination, mit der die neuen irreduziblen Basisvektoren
durch die Produktbasisvektoren ausgedrückt werden, die Clebsch-Gordan-Koezienten.
Für wichtige Fälle sind die Clebsch-Gordan-Koezienten tabelliert.
19
4
Tensoroperatoren
4.1 Denition
Viele physikalische Gröÿen sind unter der Wirkung einer Gruppe zwar nicht
invariant, haben aber ein deniertes Transformationsverhalten, wie beispielsweise die Komponenten eines Ortsvektors unter der Wirkung von SO(3). Um
später die Berechnung von Matrixelementen gruppentheoretisch vereinfachen
zu können, müssen wir zunächst eben dieses Verhalten näher untersuchen.
Denition 2 (Gruppenwirkung auf einen selbstadj. Operator) Sei
T ein selbstadjungierter Operator im Vektorraum V (mit einem inneren
Produkt h· |·i ). Sei auÿerdem G eine Gruppe mit längenerhaltender Wirkung
auf V:
G → GL(V )g 7→ D(g)
D(g)† = D(g)−1 = D(g −1 )
wobei
Dann ist der unter der Wirkung von G transformierte Operator T 0 , derjenige
für den
D(g)T = T 0 D(g)
T 0 = D(g)T D(g)−1
oder
erfüllt ist.
Damit ist eine Gruppenwirkung auf den Raum der selbstadjungierten Operatoren deniert. Man kann jetzt also die Methoden der Darstellungstheorie
anwenden.
Von groÿer Bedeutung für die Physik - besonders für die Quantenmechanik sind die Tensoroperatoren, da die den Observablen zugehörigen Operatoren
häug ein bestimmtes Transformationsverhalten besitzen.
Denition 3 (Satzo irreduzibler Tensoroperatoren) Die
n
(α)
Ti , i = 1, . . . , dα bildet genau dann einen Satz irreduzibler
Menge
Tensor(α)
operatoren (zur irreduziblen Darstellung D der Gruppe G), wenn sich
ihre Elemente unter der Wirkung von G auf folgende Art und Weise
transformieren:
(α)
D(g)Ti D(g)−1
=
dα
X
j=1
20
(α)
(α)
Dji (g)Tj
Die irreduziblen Tensoroperatoren zur Darstellung D(α) transformieren sich
also wie ein Satz von Basisfunktionen zu dieser Darstellung. Man kann also
auch sagen: Ein Satz irreduzibler Tensoroperatoren zur Darstellung D(α)
bildet eine Basis zur Darstellung D(α) .
4.2 Beispiel: Ortsoperator
Um mit dieser Denition vertraut zu werden wollen wir nun als Beispiel den
Ortsoperator behandeln.
Gesucht ist also das Transformationsverhalten des Ortsoperators unter der
Wirkung von O(3).
Dazu benötigen wir:
• Transformationsverhalten eines Vektors unter O(3):
[D(g)x]i
=
3
X
(v)
Dij (g)xj
(59)
j=1
(60)
bzw.
D(g −1 )x i
=
3
X
(v)
Dji (g)xj
(61)
j=1
• Wirkung von g ∈ G auf eine skalare Funktion:
(D(g)Ψ) (x1 , x2 , x3 ) = Ψ D(g)−1 x 1 , D(g)−1 x 2 , D(g)−1 x 3
(62)
D.h. die transformierte Funktion entspricht der unveränderten Funktion, ausgewertet am rücktransformierten Ort.
• Die Wirkung des Ortsoperators auf eine Wellenfunktion ist in der Orts-
darstellung wie folgt deniert:
x̂i Ψ(x) = xi Ψ(x)
(63)
Gemäÿ Denition 2 gilt für den mit g transformierten Orstoperator x̂0 :
D(g)x̂Ψ(x1 , x2 , x3 ) = x̂0 D(g)Ψ(x1 , x2 , x3 )
(64)
Wir berechnen jetzt die linke Seite von Gleichung (64): Mit der Wirkung des
Ortsoperators auf Wellenfunktionen ergibt sich:
Def.
x̂i Ψ(x1 , x2 , x3 ) = xi Ψ(x1 , x2 , x3 )
21
(65)
Abbildung 2: Wirkung von c6 auf die p-Wellenfunktionen der C-Atome eines
Benzolmoleküls
Setzt man weiter die Wirkung von g auf die skalare Funktion xi Ψ(x1 , x2 , x3 )
ein:
= D(g −1 )x i Ψ D(g)−1 x 1 , D(g)−1 x 2 , D(g)−1 x 3
(66)
Verwendet man das Transformationsverhalten von Ortsvektoren, so erhält
man:
=
3
X
(v)
Dji (g)xj (D(g)Ψ(x1 , x2 , x3 ))
(67)
j=1
Mit der Denition des Ortsoperators ergibt sich schlieÿlich das Resultat:
D(g)x̂i Ψ(x1 , x2 , x3 ) =
3
X
(v)
Dji (g)x̂j (D(g)Ψ(x1 , x2 , x3 ))
(68)
j=1
Für den mit g transformierten Ortsoperator gilt:
x̂0i = D(g)x̂i D(g)−1 =
3
X
(v)
Dji (g)x̂j
(69)
j=1
Die Komponenten des Ortsoperators transformieren sich also wie polare Basisvektoren zur Vektordarstellung. Sie bilden damit einen Satz irreduzibler
Tensoroperatoren bezüglich D(v) .
Weitere Beispiele für selbstadjungierte Operatoren sind:
22
∂
• Impulsoperator p̂i Ψ(x1 , x2 , x3 ) = −i~ ∂x
Ψ(x1 , x2 , x3 ):
i
p̂0 i = D(g)p̂i D(g)−1 =
3
X
(v)
Dji (g)p̂j
(70)
j=1
• Drehimpulsoperator L̂i Ψ(x1 , x2 , x3 ) = ijk x̂j p̂k Ψ(x1 , x2 , x3 ):
L̂0
i
−1
= D(g)L̂i D(g)
=
3
X
(v)
det D(v) (g) Dji (g)L̂j
(71)
j=1
Dabei transformiert sich die Komponenten des Impulsoperators unter O(3)
gleich wie die des Ortsoperators, während sich die Komponenten des Drehimpulsoperators wie axiale
Basisvektoren transformieren. D.h. gleich, bis auf
den Faktor det D(v) (g) . Unter O(3) kann dieser Faktor die Werte ±1 annehmen. Enthält die Transformation Spiegelungen, so ist er -1, sonst 1. Physikalisch kann man sich diesen Sachverhalt an einem einfachen Beispiel klarmachen.
Abbildung 3: Transformationsverhalten: axialer Vektor
In Abbildung 3 ist ein Massepunkt dargestellt, der sich auf einer Kreisbahn
bewegt. Der Drehimpulsvektor zeigt hier nach oben. Führt man eine Spiegelung an einer Ebene senkrecht zur Kreisbahn, durch den Kreismittelpunkt
aus, so bewegt sich der Massepunkt im gespiegelten Problem in entgegengesetzter Richtung. D.h. der Drehimpulsvektor zeigt jetzt nach unten. Ein
Ortsvektor wäre bei einer Spiegelung an einer Ebene, die ihn enthält, unverändert geblieben.
23
5
Wigner-Eckart-Theorem
Satz 3 (Wigner-Eckart-Theorem) Sei Ti(α) , i = 1, . . . , dα ein Satz
irreduzibler Tensoroperatoren zur irreduziblen Darstellung D(α) und
{|β, ji , j = 1, . . . dβ } bzw. {|γ, ki , k = 1, . . . dγ } ein Satz von Basisfunktionen zur irreduziblen Darstellung D(β) bzw. D(γ) . Dann gilt:
n
D
o
E
E (αβ|γ)
X D
(γ) (α) (β)
=
ϕ(γ) T (α) ϕ(β) hγsk|αi, βji
ϕk Ti ϕj
s
s=1
mit den komplex konjugierten Clebsch-Gordan-Koezienten
hγsk|αi, βji und
dem reduzierten Matrixelement ϕ(γ) T (α) ϕ(β) s , das unabhängig von den
Spaltenindizes ist.
Jetzt wollen wir das Wigner-Eckart-Theorem beweisen.
n
o
Sei also Ti(α) , i = 1, . . . , dα ein Satz irreduzibler Tensoroperatoren zur irn
E
o
reduziblen Darstellung D(α) und ϕ(β)
, j = 1, . . . dβ ein Satz von Baj
sisfunktionen zur irreduziblen Darstellung D(β) . Wir
wollen
uns zunächst
E
(α) (β)
das Transformationsverhalten der Funktionen Ti ϕj klarmachen. Dazu
lassen wir D(g) auf diese Funktionen wirken:
(α) (β)
ϕj
D(g)Ti
E
E
(β)
(α)
= D(g)Ti D(g)−1 D(g) ϕj
{z
} | {z E }
|
0(α)
(72)
0(β)
ϕj
Ti
Setzt man das bekannte Transformationsverhalten der Tensoroperatoren und
der Basisfunktionen ein, so erhält man:
E
(β)
D(g)T i(α) ϕj
=
dα
X

!  dβ
E
X
(β) 
(α)
(α) 
(β)
D (g)T
D (g) ϕ
ki
k
lj
k=1
l
(73)
l=1
Damit ergibt sich letztendlich:
(α) (β)
ϕj
D(g)Ti
E
=
X
k,l
(α)
(β)
(α) (β)
ϕl
Dki (g)Dlj (g) Tk
|
{z
}
E
(74)
(α×β)
Dkl,ij (g)
Die betrachteten Funktionen transformieren sich also nach der Produktdar
E
stellung D(α) ⊗D(β) = D(α×β) . Anders formuliert: Die Funktionen Ti(α) ϕ(β)
j
24
bilden einen Satz Basisfunktionen zur Produktdarstellung D(α×β) . Diese Produktdarstellung ist im Allgemeinen reduzibel. Wie oben beschrieben lässt
sich die
ausreduzieren, indem wir von der Produktbasis
Produktdarstellung
E
(α) (β)
in eine symmetrieangepasste Basis wechseln. Dies können wir mit
Ti ϕj
Hilfe der Clebsch-Gordan-Koezienten bewerkstelligen:
(α) (β)
Ti ϕj
E
X (γ,sγ ) E
hγsγ k |αiβji
=
Ψk
(75)
γ,sγ ,k
D
Auf diese Gleichung wollen wir nun von links ϕ(η)
m wirken lassen. Es ergibt
sich:
D
E
E
X D
(η) (α) (β)
(η) (γ,sγ )
ϕm Ti ϕj
=
ϕm Ψk
hγsγ k |αiβji
(76)
γ,sγ ,k
D
E
(γ,sγ )
Nun müssen wir noch das Skalarprodukt ϕ(η)
berechnen: Dies soll
m Ψk
hier nur für den Fall einer endlichen, diskreten Gruppe vorgerechnet werden.
Die Rechnung lässt sich jedoch auf kompakte Gruppen verallgemeinern.
Da D(g) eine unitäre Darstellung ist, gilt:
D
E D
E
(γ,sγ )
(γ,sγ )
(η) ϕ(η)
Ψ
=
D(g)ϕ
D(g)Ψ
m
m
k
k
∀g ∈ G
(77)
Da dies für alle g ∈ G gilt und G endlich und diskret ist, lässt sich das
Skalarprodukt wie folgt schreiben:
D
E
E
1 XD
(γ,sγ )
(γ,sγ )
(η) ϕ(η)
Ψ
=
D(g)Ψ
D(g)ϕ
m
m
k
k
|G|
(78)
g∈G
Setzt man das bekannte Transformationsverhalten der Basisfunktionen ein,
so ergibt sich:
=
dγ dη
E
1 X X X D (η)
(γ,s )
(η) (γ)
Djm (g)ϕj Dik (g)Ψi γ
|G|
(79)
g∈G i=1 j=1
Aus den Eigenschaften des Skalarproduktes folgt:
D
E
1 X X (η) ∗ (γ)
(η) (γ,sγ )
=
Djm (g) Dik (g) ϕj Ψi
|G|
(80)
g∈G i,j
Umordnen liefert:
=
XD
i,j
(η)
ϕj
E
(γ,sγ ) 1 X (η) ∗ (γ)
Djm (g) Dik (g)
Ψi
|G|
g∈G
|
{z
}
1
δ δ δ
dη ηγ ji mk
25
(81)
Mit der Orthogonalitätsrelation
folgt schlieÿlich:
D
(η)
∗ (γ)
g∈G Djm (g) Dik (g)
1
|G|
P
=
1
dη δηγ δji δmk
E
1 X D (η) (γ,sγ ) E
(γ,sγ )
ϕ(η)
= δηγ δmk
ϕj Ψj
m Ψk
dη
j
|
{z
}
(82)
Def.
= K (γ,sγ )
Setzt man dies in Gleichung (76) ein, so ergibt sich:
(αβ|η)
D
(η) (α) (β)
ϕk Ti ϕj
E
X
=
K (γ,sγ ) hηsk|αi, βji
(83)
s=1
Deniert man schlieÿlich K (γ,sγ ) = ϕ(η) T (α) ϕ(β) s als reduziertes Matrixelement, so erhält man das Wigner-Eckart-Theorem:
D
(η) (α) (β)
ϕk Ti ϕj
E
=
(αβ|η) D
X
E
ϕ(η) T (α) ϕ(β) hηsk|αi, βji
s
s=1
(84)
Durch das Wigner-Eckart-Theorem wird die Berechnung von Matrixelementen in zwei Teile separiert. Nämlich in die Berechnung des reduzierten Matrixelements, das nicht mehr von den Spaltenindizes abhängt, und in die
Ermittlung der Clebsch-Gordan-Koenienzen. Diese werden von der Symmetrie des Problems bestimmt. Zur Berechnung der reduzierten Matrixelemente muss man jedoch die genauen Wellenfunktionen kennen. D.h. man benötigt die vollständige physikalische Information. Mit Hilfe dieses Theorems
kann man also allein durch Betrachtung der Symmetrie Aussagen darüber
treen, ob die Matrixelemente verschwinden oder nicht (→ Auswahlregeln).
Des Weiteren erlaubt uns das Theorem, bei der Betrachtung von bestimmten Übergängen 2 , Aussagen über die Intensitätsverhältnisse zwischen diesen
Übergängen zu treen.
Insbesondere verschwinden die Clebsch-Gordan-Koezienten hηsk|αi, βji und
damit die Matrixelemente immer, wenn die irreduzible Darstellung D(η) nicht
in der Produktdarstellung D(α) ⊗ D(β) enthalten ist.
2
Solche deren Anfangszustände zu den gleichen irreduziblen Darstellungen gehören und
ebenso deren Endzustände. Dann ist das reduzierte Matrixelement für alle gleich.
26
6
Physikalische Anwendungen des Wigner-EckartTheorems
In diesem Abschnitt wollen wir uns nun um spezielle Anwendungen des
Wigner-Eckart-Theorems in der Physik kümmern.
6.1 Auswahlregeln
Eine besonders wichtige Anwendung des Wigner-Eckart-Theorems ist die Ermittlung von Auswahlregeln verschiedener Arten von Übergängen in quantenmechanischen Systemen.
6.1.1 Elektromagnetische Dipolübergänge
Wichtige Vertreter solcher Übergänge sind die elektrischen Dipolübergänge.
Wie wir in Abschnitt 2.6 gesehen haben, ist die Wahrscheinlichkeit (in erster
Ordnung), für Übergänge zwischen den Zuständen |ϕi i und |ϕf i, proportional zum Betragsquadrat des Matrixelements hϕf |V | ϕi i. Für einen elektrischen Dipolübergang wird die Störung durch eine elektromagnetische Welle
verursacht. Der zugehörige Störoperator kann auf folgende Art und Weise
dargestellt werden:
V =−
i
h
e
e
p · A = − p · A0 ei(k·x−ωt) + A∗0 e−i(k·x−ωt)
mc
mc
(85)
Dabei ist A das Vektorpotential des zeitabhängigen elektrischen Feldes, p
der Impuls-, x der Ortsoperator und k der Wellenvektor.
Es ist k · x 1, da sich h|x|i a0 in der Gröÿenordnung des Bohrschen Radius
a0 und λ = |2π
k| a0 für die betrachteten Wellenlängenbereiche (z.B. für den
optischen Bereich) wesentlich gröÿer als der Bohrsche Radius ist, lässt sich
der ortsabhängige Teil der Exponentialfunktion als konstant ansehen. Mit
A0 = − 2ωi E0 ergibt sich also näherungsweise für den Störoperator:
V =
e
p · E0 sin(ωt)
mωc
verwendet man zusätzlich, dass p =
Matrixelement:
hϕf |[x, H0 ]| ϕi i = −
m
i~
(86)
[x, H0 ] gilt, so ergibt sich für das
ie
E0 sin(ωt)(Ei − Ef ) hϕf |x| ϕi i ∝ e hϕf |x| ϕi i · E
~ωc
(87)
Zieht man die Konstante e in das Matrixelement hinein, so steht der Dipoloperator d = ex in der Mitte. ( → Dipolübergang)
27
hϕf |[x, H0 ]| ϕi i = hϕf |d| ϕi i · E
(88)
Um die Auswahlregeln unter einer bestimmten Symmetriegruppe zu bestimmen, benötigen wir jetzt nur noch das Transformationsverhalten des Ortsbzw. Dioploperators.
1. Symmetriegruppe O(3):
Wir wollen also herausnden, wann das Matrixelement hϕf |di | ϕi i, unter O(3) Symmetrie, verschwindet. Die irreduziblen Darstellungen der
Gruppe O(3) lassen sich durch die Drehimpulsquantenzahlen charakterisieren. Die Kugelächenfunktionen Yml bilden zu jedem l eine Basis
zum zugehörigen invarianten Unterraum der irreduziblen Darstellung.
Unter der Wirkung von O(3) transformiert sich der Ortsoperator und
damit auch der Dipoloperator nach den Spalten der irreduziblen Darstellung D(l=1) (g).
Die quantenmechanischen Zustände lassen sich ebenfalls nach den irreduziblen Darstellungen der Symmetriegruppe einteilen. Sie transformieren sich also auch nach den Drehimpulsdarstellungen D(l) (g). Für
die Produktdarstellung D(1) (g)⊗D(l) (g) ergibt sich folgende Zerlegung
in irreduzible Darstellungen:
D(1) (g) ⊗ D(l) (g) = D(l−1) (g) ⊕ D(l) (g) ⊕ D(l+1) (g)
(89)
Da nach dem Wigner-Eckart-Theorem nur solche Matrixelemente ungleich Null sein können, bei denen die, dem Endzustand zugehörige irreduzible Darstellung, in der Produktdarstellung von Anfangszustand
und Operator enthalten ist, können wir schon jetzt alle Übergänge ausschlieÿen, bei denen sich die Quantenzahl l um mehr als 1 ändert.
Weiterhin ist bekannt, dass der Ausgangszustand |ϕi i die Parität (−1)l
und der Ortsoperator die Parität -1 hat. Da sich xj |ϕi i nach der
Produktdarstellung transformiert, müssen die sich ergebenden, irreduziblen Darstellungen alle die Parität (−1)(l+1) haben. Der Endzustand
kann jedoch nicht gleichzeitig zur irreduziblen Darstellung D(l) (g) gehören und die Parität (−1)(l+1) haben. Der Übergang l → l ist also
nicht möglich. Deshalb reicht es im Folgenden aus, die irreduziblen
Darstellungen D(l−1) und D(l+1) zu betrachten.
Aus diesen beiden Betrachtungen erhalten wir daher die Auswahlregel
für die Quantenzahl l bei Dipolübergängen.
28
Satz 4 (Erste Auswahlregel für elektrische Dipolübergänge) Unter
O(3) Symmetrie sind elektrische Dipolübergänge nur dann möglich, wenn
sich die Drehimpulsquantenzahl l um plus oder minus 1 ändert. D.h. es sind
nur Übergänge der Form l −→ l ± 1 erlaubt.
Bisher haben wir nur untersucht, welche irreduziblen Darstellungen in
der Produktdarstellung von Ortsoperator und Anfangszustand enthalten sind und welche dieser Darstellungen mit der Parität der Endzustände verträglich sind. So kann man durch eine relativ einfache und
schnelle Betrachtung erste Schlüsse aus den Symmetrieeigenschaften
ziehen. Durch eine eingehendere Betrachtung können wir jedoch noch
mehr über die Matrixelemente erfahren. Dazu müssen wir uns die Eigenschaften der Kopplungskoezienten etwas näher anschauen.
Allgemein gilt für die Kopplungskoezienten hl3 , m3 |l2 , m2 ; l1 , m1 i unter O(3)-Symmetrie, dass sie nur von Null verschieden sind, wenn
|l2 − l1 | ≤ l3 ≤ l1 + l2 und zusätzlich m1 + m2 = m3 erfüllt ist. Da
ml ∈ {−l, −l + 1, . . . , l}, erhält man m3 ∈ {−(l1 + l2 ), . . . , l1 + l2 }.
Verwenden wir nun das Wigner-Eckart-Theorem, um die Matrixelemente zu berechnen. Für diesen Fall nimmt es folgende Form an:
D
i |lf ) D
E
E (1lX
(l=1) lf , mf dj
lf d(l=1) li hlf , mf |1j, li mi i (90)
li , mi =
s=1
s
Da die möglichen irreduziblen Darstellungen des Endzustandes höchstens einmal in der Produktdarstellung, aus der irreduziblen Darstellung zum Ortsoperator und der zum Anfangszustand, enthalten ist,
entfällt die Summe über die Multiplizitäten. Da die Clebsch-GordanKoezienten für ml=1 + mi 6= mf verschwinden und ml=1 nur die
Werte -1,0,1 annehmen kann, folgt eine zweite Auswahlregel:
Satz 5 (Zweite Auswahlregel für elektrische Dipolübergänge)
Unter O(3) Symmetrie sind elektrische Dipolübergänge nur dann möglich,
wenn sich die magnetische Quantenzahl ml um 0, plus oder minus 1 ändert.
D.h. es sind nur Übergänge der Form ml −→ ml , ml ± 1 erlaubt.
Es ergeben sich also für elektrische Dipolübergänge unter O(3)-Symmetrie
folgende, von Null verschiedene, Matrixelemente:
29
=
E
 D

 li − 1 d(l=1) li hli − 1, mi − 1 |1, −1; li , mi i
f alls
|mi − 1| ≤ li − 1


0
sonst
=
E
 D

 li − 1 d(l=1) li hli − 1, mi |1, 0; li , mi i
f alls
|mi | ≤ li − 1


0
sonst
D
E
(l=1) li − 1, mi + 1 d1
li , m i
=
E
 D

 li − 1 d(l=1) li hli − 1, mi + 1 |1, +1; li , mi i
f alls
|mi + 1| ≤ li − 1


0
sonst
D
E
(l=1) li + 1, mi − 1 d−1 li , mi
=
D
D
E
(l=1) li + 1, mi d0
li , m i
=
E
D
li + 1 d(l=1) li hli + 1, mi |1, 0; li , mi i
D
E
(l=1) li + 1, mi + 1 d1
li , m i
=
E
D
li + 1 d(l=1) li hli + 1, mi + 1 |1, +1; li , mi i
D
E
(l=1) li − 1, mi − 1 d−1 li , mi
D
E
(l=1) li − 1, mi d0
li , m i
E
li + 1 d(l=1) li hli + 1, mi − 1 |1, −1; li , mi i
Wir sehen hier, dass alle Matrixelemente und damit die Übergangswahrscheinlichkeiten immer verschwinden, wenn mindestens einer der
beiden Auswahlregeln nicht erfüllt ist. Auÿerdem sehen wir, dass Übergänge mit ∆ml = ±1 von den Komponenten d(l=1)
verursacht werden.
±1
Physikalisch entspricht dies einer Störung mit zirkular in der x-y-Ebene
polarisiertem Licht. Übergänge mit ∆m = 0 hingegen werden von der
Komponente d(l=1)
verursacht. Dies entspricht einer Störung mit line0
ar in z-Richtung polarisiertem Licht. Auch die Auswahlregel |∆l| = 1
kann physikalisch gedeutet werden. Sie spiegelt die Drehimpulserhaltung wider. Denn ein Photon besitzt den Drehimpuls ~ und wenn sich
die Drehimpulsquantenzahl um 1 ändert, ändert sich der Bahndrehimpuls damit auch um ~.
Für das konkrete Beispiel li = 1 und mi = 1, also für einen p-Zustand
mit Lz -Komponente ~mi = ~, ergeben sich also die Matrixelemente:
E
D
(l=1) 0, 0 d−1 1, 1
=
E
D 0 d(l=1) 1 h0, 0 |1, −1; 1, 1i
=
Eq
D 1
0 d(l=1) 1
3
E
D
(l=1) 2, 0 d−1 1, 1
=
E
D 2 d(l=1) 1 h2, 0 |1, −1; 1, 1i
=
Eq
D 1
2 d(l=1) 1
6
D
E
(l=1) 2, 1 d0
1, 1
=
E
D 2 d(l=1) 1 h2, 1 |1, 0; 1, 1i
=
Eq
D 1
2 d(l=1) 1
2
D
E
(l=1) 2, 2 d1
1, 1
=
E
D 2 d(l=1) 1 h2, 2 |1, +1; 1, 1i
=
E
D 2 d(l=1) 1 1
30
Vom p-Zustand mit m = 1 sind also nur Dipolübergänge in den sZustand und die d-Zustände mit m = 0, 1, 2 möglich. Man kann aus
diesem Ergebnis schlieÿlich noch die Verhältnisse der Übergangswahrscheinlichkeiten in die Zustände mit l=2 ablesen. Diese verhalten sich
so, wie die Quadrate der Kopplungskoezienten. Um die absoluten
Übergangswahrscheinlichkeiten zu erhalten, muss man schlieÿlich noch
die reduzierten Matrixelemente berechnen und dann das Ergebnis in
die oben angegebene Gleichung für die Übergangswahrscheinlichkeiten
einsetzen.
2. Symmetriegruppe D4h :
Jetzt wollen wir uns die Dipolmatrixelemente für eine niedrigere Symmetrie, nämlich D4h , anschauen. Dazu benötigen wir die Charaktertafel der Gruppe D4h und auÿerdem die Charaktere der nun reduziblen
Darstellung des Ortsoperators D(l=1) (g).
Zunächst betrachten wir die Charaktere der Darstellung D(l=1) (g).
Eine Drehung um einen Winkel ϕ, um die Achse parallel zu n, lässt sich
bei geeigneter Wahl der Basis (symmetrieangepasste Basis) in folgender
Form darstellen:

eiϕ
0
0
D(Rϕ,n ) =  0 e−iϕ 0 
0
0
1

(91)
Der Charakter, also die Spur dieser Darstellung, ist
χ(Rϕ,n ) = 1 + eiϕ + e−iϕ = 1 + 2cos(ϕ)
(92)
Da sich die Spur unter Konjugation mit anderen Gruppenelementen
nicht verändert, haben wir hier den Charakter für Drehungen um den
Winkel ϕ bestimmt. Enthält die Drehung noch zusätzlich eine Spiegelung an einer Ebene mit Normalenvektor n, so kann die Rotationsachse
orthogonal zur Spiegelebene gewählt werden und es ändert sich in der
ausreduzierten Darstellung nur der Teil entlang der Rotationsachse.
Die Darstellung hat dann die Form:

eiϕ
0
0
D(Sϕ,n ) =  0 e−iϕ 0 
0
0
−1

(93)
Für den Charakter ergibt sich also
χ(Sϕ,n ) = −1 + eiϕ + e−iϕ = −1 + 2cos(ϕ)
(94)
Zusätzlich benötigen wir noch die Charaktertafel von D4h . Diese kann
man der Literatur entnehmen:
31
D4h
A1g
A2g
A1u
A2u
B1g
B2g
B1u
B2u
Eg
Eu
E 2 C4 C2 2C20 2 C200
1
1
1
1
1
1
1
1
-1
-1
1
1
1
1
1
1
1
1
-1
-1
1
-1
1
1
-1
1
-1
1
-1
1
1
-1
1
1
-1
1
-1
1
-1
1
2
0
-2
0
0
2
0
-2
0
0
i 2 S4 σh 2 σv
1
1
1
1
1
1
1
-1
-1 -1 -1 -1
-1 -1 -1
1
1
-1
1
1
1
-1
1
-1
-1
1
-1 -1
-1
1
-1
1
2
0
-2
0
-2
0
2
0
2 σd
1
-1
-1
1
-1
1
1
-1
0
0
Jetzt müssen wir die Charaktere der nun reduziblen Darstellung D(l=1) (g)
bzgl. der Konjugationsklassen von D4h bestimmen.
D4h
(l=1)
D
|D4h
E 2 C4 C2 2C20 2 C200 i 2 S4 σh 2 σv
3
1
-1 -1
-1 -3 -1
1
1
2 σd
1
Damit zerfällt D(l=1) (g), unter D4h , in die irreduziblen Darstellungen
A2u und Eu .
D(l=1) |D4h = A2u ⊕ Eu
(95)
Da die irreduziblen Darstellungen, nach denen sich der Orts- bzw. Dipoloperator transformiert, ausschlieÿlich ungerade Parität haben, müssen auch hier alle Matrixelemente verschwinden, deren Anfangs- und
Endzustände gleiche Parität haben.
Die zu den irreduziblen Darstellungen gehörenden Basisfunktionen sind:
A2u :
Eu :
(A2u )
d(
z =d
(E )
dx u
(E )
dy u
u(A2u )
ux (Eu )
uy (Eu )
In diesem Beispiel wollen wir einen Anfangszustand betrachten, der
zur irreduziblen Darstellung Eu gehört:
|ϕi i = |ϕ(Eu , j)i
Welche Endzustände sind von diesem Zustand aus erreichbar?
Dazu ist es sinnvoll sich zunächst zu überlegen, nach welchen irreduziblen Darstellungen sich die möglichen Endzustände überhaupt transformieren können. Denn nach dem Wigner-Eckart-Theorem sind solche
Endzustände, die nicht in der Produktdarstellung aus der irreduziblen
32
Darstellung des Anfangszustandes und der des Dipoloperators auftauchen, verboten. Wir benötigen also die irreduziblen Darstellungen der
Produktdarstellung:
D(l=1) (g) ⊗ Eu = (A2u ⊕ Eu ) ⊗ Eu = (A2u ⊗ Eu ) ⊕ (Eu ⊗ Eu ) (96)
Die Ergebnisse dieser Produkte sind (z.B. in [1]) tabelliert. Es ergibt
sich:
D(l=1) (g) ⊗ Eu = Eg ⊕ A1g ⊕ A2g ⊕ B1g ⊕ B2g
(97)
|{z}
A2u ⊗Eu
|
{z
Eu ⊗Eu
}
Es sind also von Eu aus nur die Zustände A1g , A2g , B1g , B2g , Eg erreichbar. Diese sind, wie schon oben erwähnt, ausschlieÿlich Zustände
gerader Parität.
Jetzt sollen die Matrixelemente, bis auf die reduzierten Matrixelemente, berechnet werden. Da die Anteile A1g , A2g , B1g , B2g allein von
Eu ⊗ Eu erzeugt werden, benötigen wir zur Berechnung der zugehörigen Matrixelemente die Kopplungskoezienten für {ux (Eu ), uy (Eu )}⊗
{vx (Eu ), vy (Eu )} in D4h -Symmetrie. Wobei ux (Eu ) und uy (Eu ) die
Basisfunktionen sind, die mit den Komponenten des Orts- bzw. Dipoloperators zur irreduziblen Darstellung Eu indentiziert werden. vx (Eu )
und vy Eu sind die Basisfunktionen, die zum Anfangszustand zur irreduziblen Darstellung Eu gehören.
Die Kopplungskoezienten kann man folgender Tabelle entnehmen:
D4h
w(A1g )
w(A2g )
w(B1g )
w(B2g )
ux (Eu )vx (Eu )
√1
2
0
√1
2
0
ux (Eu )vy (Eu )
0
uy (Eu )vx (Eu )
0
√1
2
− √12
√1
2
√1
2
0
0
uy (Eu )vy (Eu )
√1
2
0
− √12
0
Nach dem Wigner-Eckart-Theorem ergeben sich also zum Anfangszustand Eu folgende Matrixelemente:
33
ϕ(A1g ) d(A2u ) ϕ(Eu , j)
=
D
E
(E ) ϕ(A1g ) dx u ϕ(Eu , j)
=
√1 δjx
2
A1g d(Eu ) A1g
D
E
(Eu ) ϕ(A1g ) dy ϕ(Eu , j)
=
√1 δjy
2
ϕ(A2g ) d(A2u ) ϕ(Eu , j)
=
D
E
(E ) ϕ(A2g ) dx u ϕ(Eu , j)
=
D
E
(E ) ϕ(A2g ) dy u ϕ(Eu , j)
= − √12 δjx A1g d(Eu ) A2g
0
A1g d(Eu ) A1g
0
√1 δjy
2
A1g d(Eu ) A2g
ϕ(B1g ) d(A2u ) ϕ(Eu , j)
=
0
D
E
(E ) ϕ(B1g ) dx u ϕ(Eu , j)
=
D
E
(E ) ϕ(B1g ) dy u ϕ(Eu , j)
= − √12 δjy B1g d(Eu ) B1g
ϕ(B2g ) d(A2u ) ϕ(Eu , j)
=
D
E
(E ) ϕ(B2g ) dx u ϕ(Eu , j)
=
√1 δjy
2
D
E
(E ) ϕ(B2g ) dy u ϕ(Eu , j)
=
√1 δjx
2
B2g d(Eu ) B2g
√1 δjx
2
B1g d(Eu ) B1g
0
B2g d(Eu ) B2g
Durch das Wigner-Eckart-Theorem wurde also die Berechnung von
insgesamt 24 Matrixelementen (48 wenn man die Matrixelemente mit
Endzuständen ungerader Parität auch mitzählt), auf die Berechnung
von 4 verschiedenen reduzierten Matrixelementen, vereinfacht.
Um nun schlieÿlich noch die Matrixelemente mit Endzuständen zu berechnen, die sich nach Eg transformieren, benötigen wir die Kopplungskoezienten für {u(A2u )}⊗{vx (Eu ), vy (Eu )} in D4h -Symmetrie. Denn
die irreduzible Darstellung Eg ergibt sich aus A2u ⊗ Eu .
Diese sind in folgender Tabelle dargestellt:
D4h
wx (Eg )
wy (Eg )
u(A2u )vx (Eu )
0
-1
u(A2u )vy (Eu )
Damit ergeben sich folgende Matrixelemente:
34
1
0
ϕ(Eg , x) d(A2u ) ϕ(Eu , x)
=
0
ϕ(Eg , y) d(A2u ) ϕ(Eu , x)
= −1 Eg d(A2u ) Eg
ϕ(Eg , x) d(A2u ) ϕ(Eu , y)
=
1 Eg d(A2u ) Eg
ϕ(Eg , y) d(A2u ) ϕ(Eu , y)
=
0
D
E
(E ) ϕ(Eg , i) dx u ϕ(Eu , j)
=
0
D
E
(E ) ϕ(Eg , i) dy u ϕ(Eu , j)
=
0
Hier muss man also statt 12 Matrixelementen nur ein reduziertes Matrixelement berechnen.
Physikalisch bedeuten die Ergebnisse, dass Zustände, die sich nach einer der Darstellungen A1g , A2g , B1g , B2g transformieren, nur dann erreicht werden können, wenn das anregende Lich in x,y-Richtung polarisiert ist. Zustände hingegen, die sich nach der irreduziblen Darstellung
Eg transformieren, können von Eu aus nur erreicht werden, wenn das
Anregungslicht in z-Richtung polarisiert ist.
6.1.2 Ramanübergänge
Nachdem wir einige Matrixelemente für Dipolübergänge berechnet haben,
wollen wir uns jetzt noch einer anderen Art von Übergängen zuwenden, den
Ramanübergängen. Wie bereits in den quantenmechanischen Grundlagen erläutert, basiert dieser Eekt auf der Polarisierbarkeit des betrachteten Moleküls. Daher muss hier, für die Berechnung der Matrixelemente, der Polarisierbarkeitstensoroperator α verwendet werden. Dies ist ein symmetrischer
Tensor 2. Stufe und transformiert
sich daher unter
O(3) nach der symme (l=1)
(l=1)
trisierten Produktdarstellung D
⊗D
(g). Die Charaktere dieser
+
Produktdarstellung können über folgende Formel berechnet werden:
χ[l⊗l]+ (g) =
i
1 h (l)
(χ (g))2 + χ(l) (g 2 )
2
(98)
Nun sollen Ramanübergänge in D4h -Symmetrie, von einem Anfangszustand
|ϕi i = |ϕ(Eg , j)i aus, untersucht werden.
Symmetriegruppe
D4h : Die Charaktertafel von D4h haben wir bereits
oben gesehen. Jetzt müssen wir noch die Charaktere der symmetrisierten
35
Produktdarstellung bezüglich D4h bestimmen. Die Charaktere der Darstellung D(l=1) (g) wurden ebenfalls bereits oben besprochen. Daraus lassen sich
dann nach Gleichung (98) die Charaktere der symmetrisierten Produktdarstellung bestimmen. Man erhält:
E 2 C4 C2 2C20 2 C200 i 2 S4 σh 2 σv
6
0
2
2
2
6
0
2
2
D4h
(l=1)
D
|D4h
2 σd
2
Damit lässt sich die Zerlegung in irreduzible Darstellungen berechnen. Es
ergibt sich:
h
D(l=1) ⊗ D(l=1)
i
+
(99)
(g) = 2A1g ⊕ B1g ⊕ B2g ⊕ Eg
Die zugehörigen Basisfunktionen haben folgende Gestalt:
A1g :
(1)
√1 αzz
3
u(1) (A1g )
u(2) (A1g )
(αxx − αyy )
u(B1g )
αxy = αyx
u(B2g )
ux (Eg )
uy (Eg )
A1g :
(2)
1
√
2 2
B1g :
1
2
B2g :
Eg :
(αxx + αyy )
αxz = αzx
αyz = αzy
Dabei transformieren sich die Komponenten des Polarisierbarkeitstensors αij
wie die kartesischen Produktfunktionen xi xj .
Von einem Anfangszustand aus, der sich nach der Darstellung Eg transformiert, sind also Endzustände erreichbar, die sich nach einer der irreduziblen
Darstellungen der Produktdarstellung transformieren.
(2A1g ⊕ B1g ⊕ B2g ⊕ Eg ) ⊗ Eg =
2Eg ⊕ Eg ⊕ Eg ⊕
|{z}
|{z}
|{z}
2A1g ⊗Eg
B1g ⊗Eg
B2u ⊗Eg
A1g ⊕ A2g ⊕ B1g ⊕ B2g
{z
}
|
Eg ⊗Eg
= 4Eg ⊕ A1g ⊕ A2g ⊕ B1g ⊕ B2g
(100)
36
Die Endzustände können sich also nur nach folgenden irreduziblen Darstellungen transformieren (nach allen mit gerader Parität):
Eg ,
A1g ,
A2g ,
B1g ,
B2g
Alle Matrixelemente mit anderen Endzuständen verschwinden.
Beispielhaft sollen jetzt die Matrixelemente für einen Endzustand berechnet
werden, der sich nach A1g transformiert. Ein solcher Zustand kann in diesem
Fall nur vom Produkt der Basisfunktionen zu Eg mit anderen Basisfunktionen zu Eg aufgebaut werden. Wir benötigen also wieder die Kopplungskoefzienten für {ux (Eg ), uy (Eg )} ⊗ {vx (Eg ), vy (Eg )} in D4h -Symmetrie. Diese
sind im obigen Beispiel bereits angegeben. Sie seien an dieser Stelle nur für
die hier interessante irreduzible Basisfunktion w(A1 ) wiederholt.
D4h
w(A1g )
ux (Eu )vx (Eu )
ux (Eu )vy (Eu )
√1
2
0
uy (Eu )vx (Eu )
0
uy (Eu )vy (Eu )
√1
2
Für den Übergang Eg ↔ A1g sind also von den zwölf möglichen Matrixelementen nur zwei verschieden von Null:
D
E
(E ) ϕ(A1g ) αx g ϕ(Eg , j)
=
√1 δjx
2
D
E
(E ) ϕ(A1g ) αy g ϕ(Eg , j)
=
√1 δjy
2
A1g α(Eg ) A1g
A1g α(Eg ) A1g
Da das reduzierte Matrixelement in beiden Fällen das gleiche ist, muss man
also insgesamt für diesen Übergang anstatt zwölf nur ein reduziertes Matrixelement berechnen.
6.2 Eigenwertprobleme
Ein in vielen Bereichen der Physik sehr häug auftretendes Problem besteht
im Lösen von Eigenwertproblemen. Wie wir gleich sehen werden, folgt bei
Eigenwertproblemen die Blockdiagonalform einer Matrix in einer symmetrieangepassten Basis, als einfacher Spezialfall, direkt aus dem Wigner-EckartTheorem. Zwar kann mit Hilfe des Wigner-Eckart-Theorems im Allgemeinen
keine vollständige Diagonalisierung erreicht werden, wohl aber Blockdiagonalform. Somit wird das groÿe Eigenwertproblem in einige kleine Eigenwertprobleme zerlegt. Dies ist in den meisten Fällen, vom Rechenaufwand her,
eine beträchtliche Vereinfachung.
Beispielsweise bei der Lösung der Schrödingergleichung liegt ein solches Problem vor:
H |Ψi = E |Ψi
(101)
37
Dabei ist H der Hamiltonoperator des Systems, E der zugehörige Energieeigenwert und |Ψi eine Eigenfunktion zu E. Der Hamiltonoperator sei nun
invariant unter der Gruppe G, die auf den Hilbertraum V der quadratintegrablen Funktionen wirkt. Also ist:
(102)
D(g)HD(g)−1 = H
Damit ist H ein irreduzibler Tensoroperator 0. Ordnung und transformiert
sich nach der trivialen Darstellung. Transformiert man das Eigenwertproblem
in eine, der Symmetrie angepassten, Basis {|αsα ii} und wendet von links
hβsβ j| auf die Gleichung an, so erhält man:
X
(103)
hβsβ j| H |αsα ii hαsα i |Ψi = E hβsβ j| Ψi
α,sα ,i
Das Wigner-Eckart-Theorem lautet für diesen Fall:
(1α|β)=δαβ
hβsβ j| H |αsα ii =
X
s=1
(104)
hβsβ kHk αsα is hβ, j|11, αii
|
{z
}
=δαβ δij
Vereinfacht ergibt sich:
(105)
hβsβ j| H |αsα ii = s0α kHk sα δαβ δij
D.h. die zu diagonalisierende Matrix zerfällt in Blöcke, von denen einige
sogar noch gleich sind! Man erhält also das vereinfachte Problem:
(106)
X
s0α kHk sα hαsα i |Ψi = E hβsβ j| Ψi
sα
Zur Veranschaulichung wollen wir uns nun die Matrix (hs0α kHk sα i) nochmal
in ihrer Blockdiagonalform anschauen.

hs01 kHk s1 i













0
..
.
0
...
···
hs0i kHk si i
..
.
..
.
···
···
···
...
···
0
38

0













..
.
...
0
0
..
.
..
.
...
0
0
···
0
hs0r
0
kHk sr i
(107)
Die Matrix besteht jetzt aus d1 identischen Blöcken, die zur irreduziblen
Darstellung D(1) gehören, sie haben daher die Dimension m1 . Wobei m1
die Anzahl der invarianten Unterräume des Hilbertraumes ist, die sich nach
der irreduziblen Darstellung "1"transformieren. Dann aus d2 identischen
Blöcken zur irreduziblen Darstellung D(2) , usw. Man erhält also r verschiedene Blöcke, wenn r die Anzahl der verschiedenen irreduziblen
DarstelPr
d
lungen
von
G
ist.
D.h.
man
muss
jetzt
nicht
mehr
eine
(
α=1 α mα ) ×
Pr
( α=1 dα mα )-Matrix diagonalisieren, sondern nur noch r (mα ×mα )-Matrizen
(wobei α = 1, . . . , r). Dies bewirkt in der Praxis eine enorme Ersparnis an
Rechenaufwand und macht die Lösung mancher Probleme, bei denen Matrizen sehr hoher Dimension auftreten, überhaupt erst möglich.
Nebenbemerkung: Symmetriebedingte Entartung In jedem dieser Blökke erhält man im Allgemeinen mα verschiedene Eigenwerte. Da jedoch dα identische Blöcke
auftreten, sind diese Eigenwerte jeweils dα -fach entartet. Hier spricht man von symmetriebedingter Entartung, da sie alleine durch die Symmetrie des Problems gegeben ist3 . Es
kann jedoch nicht prinzipiell ausgeschlossen werden, dass beispielsweise Eigenwerte, die
zu unterschiedlichen irreduziblen Darstellungen gehören, zufällig zusammenfallen. Hier
spricht man von zufälliger Entartung. Eine solche tritt z.B. auf, wenn man die Beträge
der Eigenwerte durch einen von Aussen vorgegebenen Parameter steuern kann, wie z.B.
durch ein angelegtes Magnetfeld. Bei geeigneter Magnetfeldstärke kann es so zur Überschneidung von Eigenwerten kommen. Eine andere Möglichkeit, wie es zu einer weiteren
Entartung kommen kann, ist die, dass die betrachtete Symmetriegruppe nicht die vollständige Symmetriegruppe des Systems ist.
3
Wir haben keine physikalischen Kenntnisse des Systems in die Betrachtung einieÿen
lassen.
39
7
Zusammenfassung
Im Rahmen dieser Ausarbeitung haben wir gesehen, wie man die Berechnung
von Matrixübergangselementen durch Symmetriebetrachtungen vereinfachen
kann. Ein sehr mächtiges Werkzeug hierfür ist das Wigner-Eckart-Theorem,
mit dessen Hilfe man die Berechnung von Matrixelementen in einen Teil
zerlegen kann, der nur noch von der Symmetrie des Problems abhängt und
in einen Teil in dem die physikalische Information enthalten ist. Man kann so
allein durch Betrachtung der Symmetrie schon voraussagen, dass bestimmte
Matrixelemente verschwinden. Daraus lassen sich dann Auswahlregeln für
bestimmte Übergänge ableiten.
40
Literatur
[1] M. Wagner, Gruppentheoretische Methoden in der Physik
Ÿ9
[2] W. Ludwig und C. Falter, Symmetries in Physics Ÿ5 - Ÿ8
[3] H.-R. Trebin, Vorlesungsaufschrieb "Gruppentheoretische
Methoden in der Physik"
[4] C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantenmechanik 1 & 2
[5] M. Hamermesh, Group Theory an its Application to Physical Problems
41