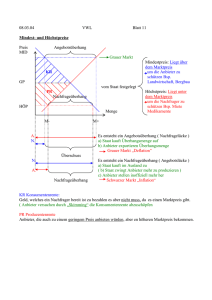
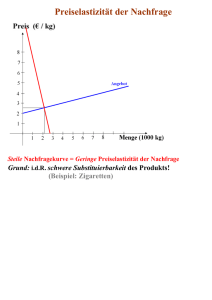
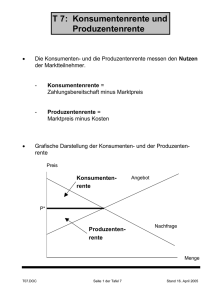
Kein Folientitel

Wirtschaft und Integralrechnung
Nachfragefunktion: N(p)
pu : Mindestens Preis
p0 : Höchstpreis
N(p) monoton fallend in [pu ; p0]
Ein Monopolist will seinen Umsatz maximieren. Dies
geschieht mittels folgender Preisfestsetzungsstrategie:
DISKRETE Preissenkung
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
1
Wirtschaft und Integralrechnung
Monopolist für maximalen Umsatz:
Anfangspreis p0 Umsatz = N(p0)*p0
1. Preissenkung: p0  p0 - p
Bei diesem Preis ist die Nachfrage N(p0-p)
Also extra Nachfrage N(p0-p) – N(p0) und
extra Umsatz = (N(p0-p) – N(p0))*(p0-p)
2. Preissenkung: p0 - p  p0 – 2*p
Bei diesen Preis Nachfrage N(p0-2p)
Also extra Nachfrage N(p0-2p) – N(p0-p) und
extra Umsatz = (p0-2p) * (N(p0-2p) – N(p0-p))
Und so senkt der Monopolist den Preis weiter bis pu
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
2
Wirtschaft und Integralrechnung
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
3
Wirtschaft und Integralrechnung
Beispiel:
Nachfrage N(P) = 2000 – 10p p  [80 ; 100]
p = 1€
N(p – 1) – N(p) = N(99) – N(100) = 1010 - 1000 = 10 ME
Umsatz = p0*N(p0)* + p0 - p *(N(p0-p) – N(p0)) +
(p0-2p)*(N(p0-2p) – N(p0-p)) +…
U=
100*N(100) + (100 – 1)* (N(99) - N(100)) +
(100 – 2)*(N(98) - N(99)) + …….. +
+ (100-20)*(N(80) - N(81)) =
U = 100*1000 + 99*10 + 98*10 + … + 80*10
U = 117900 €
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
4
Wirtschaft und Integralrechnung
Bei stetiger Preissenkung, wird der Gesamtumsatz:
p0
U  pu  N(p )   N(p )dp
pu
 80  1200  2000p  5p

2 100
80
 118000
Bei stetiger Preissenkung ist der Umsatz maximal,
je größer die Schritte bei die Preissenkung,
je kleiner der Umsatz.
Stetige Preissenkungen in der Realität nicht möglich !!!
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
5
Konsumentenrente
Normalerweise entsteht durch das Wechselspiel
zwischen Nachfragefunktion und Angebotsfunktion
ein Gleichgewichtspreis:
der Marktpreis pM
Dann gilt: A(pM) = N(pM)
Der Umsatz ist dann: U = pM*N(pM)
Manche Konsumenten wären allerdings auch bereit
einen höheren Preis als den Marktpreis pM zu zahlen.
Bei einer stetigen Preisreduzierung vom Höchstpreis p0
bis zum Marktpreis pM wäre ein zusätzlicher Umsatz
p0
erreichbar
K   N(p )dp
pM
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
6
Konsumentenrente
Falls die gesamte Ware zum Marktpreis pM angeboten
wird, sparen die Abnehmer den Betrag K,
daher heißt K die Konsumentenrente.
Konsumentenrente
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
7
Produzentenrente
Manche Produzenten wären allerdings auch bereit
unter dem Marktpreis pM zu verkaufen. Dadurch, dass
sie den Marktpreis pM erhalten, erzielen sie
Mehreinnahmen. Bei einer stetigen Preiserhöhung
vom Minimumpreis pu bis zum Marktpreis pM wäre der
pM
Gesamtumsatz
P
 A(p)dp
pu
kleiner als der Umsatz, der erzielt wurde, wenn
anstelle der stetigen Preiserhöhung sofort der
Marktpreis festgesetzt wird. Diese von allen
Anbietern durch den Verkauf beim Marktpreis erzielte
Mehreinnahme P heißt die Produzentenrente
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
8
Produzentenrente
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
9
C26
1 2 1
9
A(p)  p  p 
4
2
4
p  1;
N(p) = 8 – 0,08p2
Marktpreis: A(p) = N(p) 
1 2 1
9
p  p   8  0,08p 2  0,33p 2  0,5p  5,75  0
4
2
4
 33p2 – 50p – 575 = 0  p = 5  p = 
115
D
33
Also Marktpreis pM=5;
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
10
C26
Konsumentenrente gefragt für p  p0 =10
K
p0

pM
N(p )dp 
10

5


10
0,08 3 

8  0,08p dp   8p 
p  
3

5
2
80  
0,08 125 

 80     40 

3 
3


160
10 50

 40 

 16,67
3
3
3
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
11
C26
Produzentenrente gefragt für p  pu = 1
pM
5
5
9
1 2 1
 1 3 1 2 9 
P  A(p)dp   p  p  dp   p  p  p 
4
2
4
4
4 1
 12
pu
1


 125 25 45   1 1 9  125  75  135 1  3  27

      

4   12 4 4 
12
12
 12 4
185 25 160 40

 

 13,33
12 12 12
3
Dennis Wörmann - MR_1D03BD - Quartester 3 - Differenzieren
12