01 - Aufbau(1)_neu

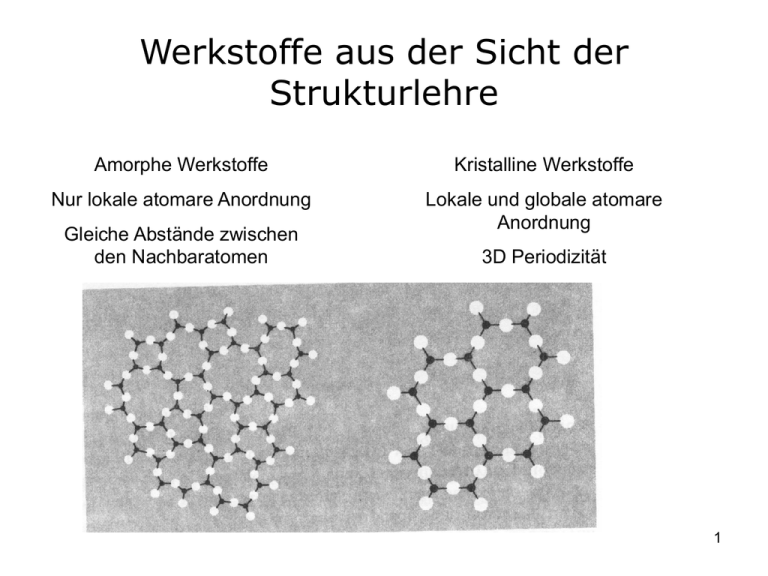
Werkstoffe aus der Sicht der
Strukturlehre
Amorphe Werkstoffe
Kristalline Werkstoffe
Nur lokale atomare Anordnung
Lokale und globale atomare
Anordnung
Gleiche Abstände zwischen
den Nachbaratomen
3D Periodizität
1
Periodizität in kristallinen Werkstoffen
Eindimensional
Dreidimensional
t3
t1
x  x0  nt1
t2
Zweidimensional
t1
x  x0  n1t1 



  
y  y0  n2t2  P  P0  n1t1  n2t2  n3t3
z  z0  n3t3 

t2
t1
x  x0  n1t1
y  y0  n2t2
2
Kristallchemische Bindungskräfte
 Van der Waals: He, Ne, Ar, Kr, Xe, Rn
 Coulombische Kraft: Ionenkristalle – NaCl, LiF, NaI,
CsCl
 Metallische Bindung – positiv geladene „Atome“, die in
ein Elektronengas eingebettet sind; schwache Bindung.
 Kovalenzbindung: starke Bindung zwischen Elektronen
– Diamant, Si, Ge
Bestimmen die mechanischen, optischen, thermischen
und magnetischen Eigenschaften der Werkstoffe
Festkörperphysik und Festkörperchemie
3
Van der Waals Bindung
Lennard-Jones Potential
  12   6 
U R   4      
 R  
 R 
Repulsive
(abstoßende)
Kraft
Anziehungskraft
4
Ionenkristalle
Wechselwirkung zwischen positiv und negativ geladenen Ionen
12
q2
 
U R   4   
R
R
Repulsive
(abstoßende)
Kraft
Anziehungskraft
(Coulomb Potential)
Starke Bindung  Ionenkristalle sind hart und haben einen hohen
Schmelzpunkt
5
Metalle
 Elektronen werden unter Atomen geteilt – gute
elektrische Leitfähigkeit und Temperaturleitfähigkeit,
Undurchsichtigkeit, hohe optische Reflektivität (Glanz)
 Die Energie im kondensierten Zustand ist kleiner als die
Summe der Energien einzelner Atome
6
Kovalente Kristalle
 Die Atome in der Kovalenzbindung tragen jeweils mit
einem Elektron zu der Bindung bei
 Als Folge der Kovalenzbindung beobachtet man
tetraedrische Anordnung der Atome – jedes Atom ist in
der Regel an 4 andere Atome gebunden
7
Wie kann man die Kristallstruktur
vorhersagen?
 Aus der Affinität oder Elektronenkonfiguration der
beteiligten Atome (Quantenmechanik)
 Aus der Anzahl an Valenzelektronen
 Aus der Größe der Atome (aus den Atomradien)
8
2r
2r
2 r.√2
2 r.√2
Maximale Größe des inneren Atoms


R  2r 3  2r  2r 3  1  0,73  r
2 r.√3
2r
9
Oktaedrische Atomlage
2r
2 r.√2
2r
Maximale Größe des inneren Atoms
R  2r 2  2r  2r


2  1  0,414  r
10
Tetraedrische Atomlage
d 2  (OB  d ) 2  (OA) 2
(OB ) 2  (OA) 2
d
2(OB )
OA 
d
8
3
2 3
2
R ; OB  2 R
3
3
R 2  43 R 2
4R
Maximale Größe des
inneren Atoms
r d R
2
3

3
2

3R
2

 1 R  0,22  R
11
Atomzahl
12