Einführung in die Differenzialrechnung
Werbung

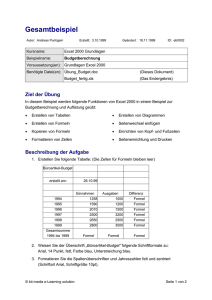
mit dem „Freien Fall“ und der Geschwindigkeit Denken wir an Geschwindigkeit, so fällt uns sofort Kilometer pro Stunde ein. Das ist auch gleich die Formel der Geschwindigkeit: 𝐺𝑒𝑠𝑐ℎ𝑤𝑖𝑛𝑑𝑖𝑔𝑘𝑒𝑖𝑡 = 𝑊𝑒𝑔𝑠𝑡𝑟𝑒𝑐𝑘𝑒 𝑍𝑒𝑖𝑡 𝑣= 𝑠 𝑡 Na, ganz einfach – man schaut hinaus und sieht die Kilometersteine, die die Entfernung (von z.B. Wien) anzeigen. Dann muss man nur mehr die Zeit zwischen dem Vorbeifahren an zwei Kilometersteinen messen Das ergibt zum Beispiel: Kilometerstein 103 wird um 17:35 gesehen Kilometerstein 104 wird um 17:36 gesehen Die Geschwindigkeit ergibt sich daraus als Bruch: 𝐺𝑒𝑠𝑐ℎ𝑤𝑖𝑛𝑑𝑖𝑔𝑘𝑒𝑖𝑡 = 104−103 17:36−17:35 Wie viel ist das in km/h ? > = 1 1 𝑘𝑚/𝑚𝑖𝑛 Das ergibt zum Beispiel: Kilometerstein 103 wird um 17:35 gesehen Kilometerstein 104 wird um 17:36 gesehen Die Geschwindigkeit ergibt sich daraus als Bruch: 𝐺𝑒𝑠𝑐ℎ𝑤𝑖𝑛𝑑𝑖𝑔𝑘𝑒𝑖𝑡 = 104−103 17:36−17:35 = 1 1 𝑘𝑚/𝑚𝑖𝑛 Wie viel ist das in km/h ? 60 km/h zu langsam für die Autobahn! Daraus folgt die Definition der mittleren Geschwindigkeit – im Zeitintervall [ta; te] für die Wegabschnitte s(ta) und s(te) v [ta; te] = 𝑊𝑒𝑔𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑧 𝑍𝑒𝑖𝑡𝑑𝑖𝑓𝑓𝑒𝑟𝑒𝑛𝑧 = 𝑠 𝑡𝑒 −𝑠(𝑡𝑎 ) 𝑡𝑒 −𝑡𝑎 eines Steins wird mit folgender Tabelle gegeben: Zeit Wegstrecke 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m eines Steins wird mit folgender Tabelle gegeben: Zeit Wegstrecke 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m Wie kann man eine Formel für die Wegstrecke aufstellen? eines Steins wird mit folgender Tabelle gegeben: Zeit Wegstrecke 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m Wie kann man eine Formel für die Wegstrecke aufstellen? Dazu dividieren wir die Zahlen der Wegstrecke durch 5 eines Steins wird mit folgender Tabelle gegeben: Zeit Wegstrecke durch 5 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m 1 4 9 16 25 Wie kann man eine Formel für die Wegstrecke aufstellen? Dazu dividieren wir die Zahlen der Wegstrecke durch 5 eines Steins wird mit folgender Tabelle gegeben: Zeit Wegstrecke durch 5 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m 1 4 9 16 25 Nun sieht man, dass die neuen Zahlen die Quadrate der Zeiten (also t²) sind, daher ergibt sich die Formel für die Wegstrecke: eines Steins wird mit folgender Tabelle gegeben: Zeit Wegstrecke durch 5 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m 1 4 9 16 25 Die Formel für die Wegstrecke ist: s(t) = 5*t² Zeit Wegstrecke 1s 2s 3s 4s 5s 5m 20 m 45 m 80 m 125 m Wir wollen die mittlere Geschwindigkeit im Zeitintervall [2;4] bestimmen. Dazu müssen wir die Wegdifferenz durch die Zeitdifferenz dividieren: Zeit 1s 2s 3s 4s 5s Wegstrecke durch 5 5m 20 m 45 m 80 m 125 m 1 4 9 16 25 Wir wollen die mittlere Geschwindigkeit im Zeitintervall [2;4] bestimmen. Dazu müssen wir die Wegdifferenz durch die Zeitdifferenz dividieren: 𝑠 4 − 𝑠(2) 80 − 20 60 𝑣 2; 4 = = = = 30 𝑚/𝑠 4−2 4−2 2 𝑣 2; 4 = 𝑠 4 −𝑠(2) 4−2 = 80−20 4−2 = 60 2 = 30 𝑚/𝑠 Dazu ersetzen wir nur die konkreten Zahlen für die Zeit (2 und 4) durch die Buchstaben a und e (für Anfangszeit und Endzeit) 𝑣 2; 4 = 𝑠 4 −𝑠(2) 4−2 = 80−20 4−2 = 60 2 = 30 𝑚/𝑠 Dazu ersetzen wir nur die konkreten Zahlen für die Zeit (2 und 4) durch die Buchstaben a und e (für Anfangszeit und Endzeit) Und außerdem die Strecken durch die Formel s(t) = 5*t² 𝑣 2; 4 = 𝑠 4 −𝑠(2) 4−2 = 80−20 4−2 = 60 2 = 30 𝑚/𝑠 Dazu ersetzen wir nur die konkreten Zahlen für die Zeit (2 und 4) durch die Buchstaben a und e (für Anfangszeit und Endzeit) Und außerdem die Strecken durch die Formel s(t) = 5*t² 𝑣 𝑎; 𝑒 = 𝑠 𝑒 −𝑠(𝑎) 𝑒−𝑎 = 5∗𝑒 2 −5∗𝑎² 𝑒−𝑎 𝑣 2; 4 = 𝑠 4 −𝑠(2) 4−2 = 80−20 4−2 = 60 2 = 30 𝑚/𝑠 Dazu ersetzen wir nur die konkreten Zahlen für die Zeit (2 und 4) durch die Buchstaben a und e (für Anfangszeit und Endzeit) Und außerdem die Strecken durch die Formel s(t) = 5*t² 𝑣 𝑎; 𝑒 = 𝑠 𝑒 −𝑠(𝑎) 𝑒−𝑎 = 5∗𝑒 2 −5∗𝑎² 𝑒−𝑎 Wie können wir das noch vereinfachen? 𝑣 𝑎; 𝑒 = 𝑠 𝑒 −𝑠(𝑎) 𝑒−𝑎 = 5∗𝑒 2 −5∗𝑎² 𝑒−𝑎 𝑣 𝑎; 𝑒 = 𝑠 𝑒 −𝑠(𝑎) 𝑒−𝑎 = 5∗𝑒 2 −5∗𝑎² 𝑒−𝑎 Dazu werden wir 5 herausheben 5 ∗ (𝑒 2 − 𝑎2 ) 𝑣 𝑎; 𝑒 = 𝑒−𝑎 𝑣 𝑎; 𝑒 = 𝑠 𝑒 −𝑠(𝑎) 𝑒−𝑎 = 5∗𝑒 2 −5∗𝑎² 𝑒−𝑎 Dazu werden wir 5 herausheben 5 ∗ (𝑒 2 − 𝑎2 ) 5 ∗ 𝑒 − 𝑎 ∗ (𝑒 + 𝑎) 𝑣 𝑎; 𝑒 = = 𝑒−𝑎 (𝑒 − 𝑎) und die Binomische Formel benutzen. 𝑣 𝑎; 𝑒 = 𝑠 𝑒 −𝑠(𝑎) 𝑒−𝑎 = 5∗𝑒 2 −5∗𝑎² 𝑒−𝑎 Dazu werden wir 5 herausheben 5 ∗ (𝑒 2 − 𝑎2 ) 5 ∗ 𝑒 − 𝑎 ∗ (𝑒 + 𝑎) 𝑣 𝑎; 𝑒 = = 𝑒−𝑎 (𝑒 − 𝑎) und die Binomische Formel benutzen. Und dann kürzen: 𝑣 𝑎; 𝑒 = 5*(e+a) Mit der Formel der mittleren Geschwindigkeit 𝑣 𝑎; 𝑒 = 5*(e+a) können wir nun auch die momentane Geschwindigkeit berechnen. Mit der Formel der mittleren Geschwindigkeit 𝑣 𝑎; 𝑒 = 5*(e+a) können wir nun auch die momentane Geschwindigkeit berechnen. Dazu brauchen wir nur mehr den Wert des Endzeitpunktes e immer näher an den Anfangszeitpunkt a annähern (in der Mathematik ist das der LIMES=Grenzwert) Mit der Formel der mittleren Geschwindigkeit 𝑣 𝑎; 𝑒 = 5*(e+a) können wir nun auch die momentane Geschwindigkeit berechnen. Dazu brauchen wir nur mehr den Wert des Endzeitpunktes e immer näher an den Anfangszeitpunkt a annähern (in der Mathematik ist das der LIMES=Grenzwert) 𝑣 𝑎 = lim 5 ∗ 𝑒 + 𝑎 = 5 ∗ 𝑎 + 𝑎 = 10 𝑎 𝑒→𝑎 𝑣 𝑎 =10 a ist die Formel für die momentane Fallgeschwindigkeit zum Zeitpunkt a 𝑣 𝑎 =10 a ist die Formel für die momentane Fallgeschwindigkeit zum Zeitpunkt a Berechnet man damit die Geschwindigkeit des fallenden Steins nach 2 Sekunden, so ergibt sich v(2) = 10∙2 = 20 m/s Mit 3,6 multipliziert ergibt das v(2) = 72 km/h 𝑣 𝑎 =10 a ist die Formel für die momentane Fallgeschwindigkeit zum Zeitpunkt a Berechnet man damit die Geschwindigkeit des fallenden Steins nach 2 Sekunden, so ergibt sich v(2) = 10∙2 = 20 m/s Mit 3,6 multipliziert ergibt das v(2) = 72 km/h Dasselbe für die Zeit t=4 ergibt v(4) = 10∙4 = 40 m/s = 1440 km/h Wir haben aus der Formel der Fallbewegung s(t) = 5*t² die Geschwindigkeit v(t) = 10*t hergeleitet. Können wir das jetzt auch für andere Formeln machen? Wir haben aus der Formel der Fallbewegung s(t) = 5*t² die Geschwindigkeit v(t) = 10*t hergeleitet. Können wir das jetzt auch für andere Formeln machen? Ja – dazu machen wir eine Tabelle: Typ Wegfunktion Geschwindigkeit Stehen in 3m Entfernung s(t) = 3 v(t) = 0 Gehen mit 2 m/s s(t) = 2t v(t) = 2 Fallen s(t) = 5t² v(t) = 10t Beschleunigen s(t) = t³ v(t) = 3t² Allgemein s(t) = a*tn v(t) = a*n*tn−1 Jetzt können wir das Thema Geschwindigkeit auf allgemeine Funktionen erweitern: Dann sind die Funktionen f(x) = x² Jetzt können wir das Thema Geschwindigkeit auf allgemeine Funktionen erweitern: Dann sind die Funktionen f(x) = x² und die „Geschwindigkeiten“ f‘(x) = 2x Jetzt können wir das Thema Geschwindigkeit auf allgemeine Funktionen erweitern: Dann sind die Funktionen f(x) = x² und die „Geschwindigkeiten“ f‘(x) = 2x Und heißen: momentane Änderungsrate Jetzt können wir das Thema Geschwindigkeit auf allgemeine Funktionen erweitern: Dann sind die Funktionen f(x) = x² und die „Geschwindigkeiten“ f‘(x) = 2x Und heißen: momentane Änderungsrate oder: 1.Ableitung Jetzt können wir das Thema Geschwindigkeit auf allgemeine Funktionen erweitern: Dann sind die Funktionen f(x) = x² und die „Geschwindigkeiten“ f‘(x) = 2x Und heißen: momentane Änderungsrate oder: 1.Ableitung oder: Differenzialquotient 𝑓 𝑒 −𝑓(𝑎) lim 𝑒−𝑎 𝑒→𝑎 Dann kommen die Ableitungsregeln Dann kommen die Ableitungsregeln Und die grafische Betrachtung (Steigung) Dann kommen die Ableitungsregeln Und die grafische Betrachtung (Steigung) Und viele viele Beispiele und Anwendungen (Kurvendiskussion, Extremwertaufgaben, Wirtschaftsfunktionen, physikalische…) Dann kommen die Ableitungsregeln Und die grafische Betrachtung (Steigung) Und viele viele Beispiele und Anwendungen (Kurvendiskussion, Extremwertaufgaben, Wirtschaftsfunktionen, physikalische…) UND DAS WAR ES! (Liebe Grüße von Manfred)