Vergleich R2-R3 - Antonkriegergasse
Werbung
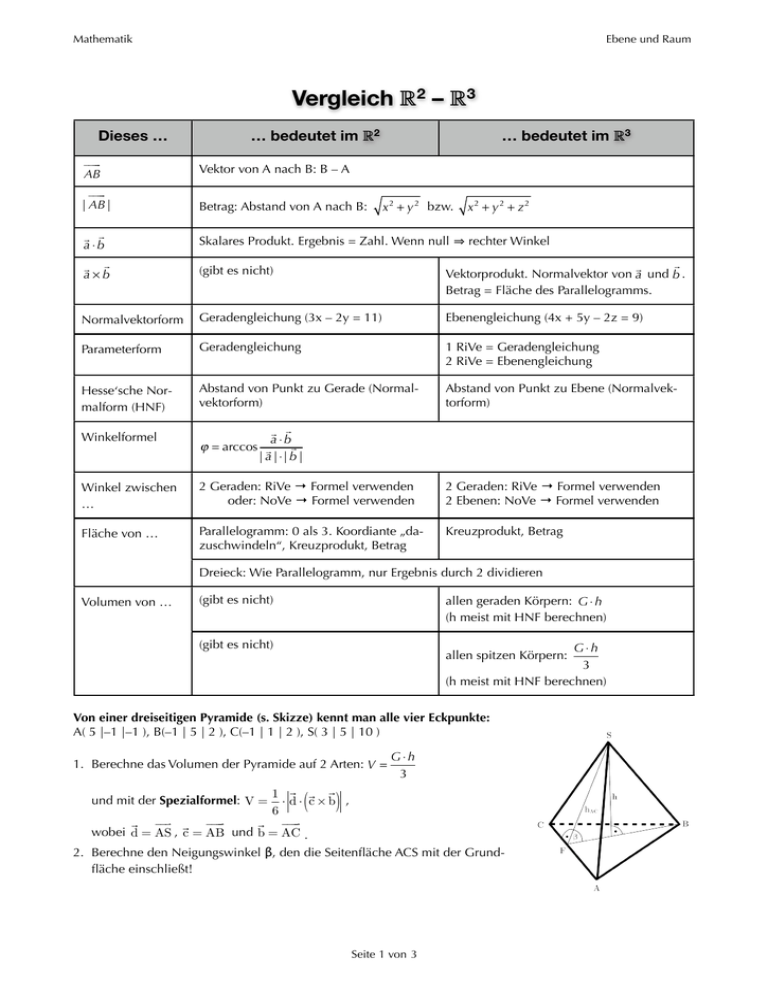
Mathematik Ebene und Raum Vergleich R2 – R3 Dieses … … bedeutet im R2 … bedeutet im R3 AB Vektor von A nach B: B – A | AB | Betrag: Abstand von A nach B: a ⋅b Skalares Produkt. Ergebnis = Zahl. Wenn null a×b (gibt es nicht) Normalvektorform Geradengleichung (3x – 2y = 11) Ebenengleichung (4x + 5y – 2z = 9) Parameterform Geradengleichung 1 RiVe = Geradengleichung 2 RiVe = Ebenengleichung Hesse‘sche Normalform (HNF) Abstand von Punkt zu Gerade (Normalvektorform) Abstand von Punkt zu Ebene (Normalvektorform) Winkelformel x 2 + y 2 bzw. x 2 + y 2 + z2 rechter Winkel Vektorprodukt. Normalvektor von a und b . Betrag = Fläche des Parallelogramms. a ⋅b ϕ = arccos | a | ⋅| b | Winkel zwischen … 2 Geraden: RiVe → Formel verwenden oder: NoVe → Formel verwenden 2 Geraden: RiVe → Formel verwenden 2 Ebenen: NoVe → Formel verwenden Fläche von … Parallelogramm: 0 als 3. Koordiante „dazuschwindeln“, Kreuzprodukt, Betrag Kreuzprodukt, Betrag Dreieck: Wie Parallelogramm, nur Ergebnis durch 2 dividieren Volumen von … (gibt es nicht) allen geraden Körpern: G ⋅ h (h meist mit HNF berechnen) (gibt es nicht) G⋅h 3 (h meist mit HNF berechnen) allen spitzen Körpern: Von einer dreiseitigen Pyramide (s. Skizze) kennt man alle vier Eckpunkte: A( 5 |–1 |–1 ), B(–1 | 5 | 2 ), C(–1 | 1 | 2 ), S( 3 | 5 | 10 ) 1. Berechne das Volumen der Pyramide auf 2 Arten: V = G⋅h 3 1 ⋅ d ⋅ c×b , 6 wobei d = AS , c = AB und b = AC . und mit der Spezialformel: V = ( ) 2. Berechne den Neigungswinkel β, den die Seitenfläche ACS mit der Grundfläche einschließt! Seite 1 von 3 Mathematik Ebene und Raum Zuerst Grundfläche G berechnen: <- im TR speichern! Die Höhe ist der Abstand von der Grundfläche (=Ebene) zum Punkt S: <- im TR speichern! Seite 2 von 3 Mathematik Ebene und Raum Da jetzt G und h berechnet sind, braucht man nur mehr in die Formel G⋅h einsetzen: 3 Jetzt dasselbe mit der Spezialformel: Nun kommt die Berechnung des Winkels dran. Es sind 2 Ebenen, zwischen denen der Winkel gesucht ist: Seite 3 von 3