Zusammenfassung - Antonkriegergasse

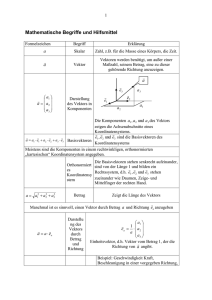
Vektorgeometrie
Koordinaten eines Punktes
Anfangspunkt + Pfeil dorthin
Pfeil von A nch B
B–A
Mittelpunkt der Streche AB
A+B
2
Schwerpunkt eines Dreiecks
A+B+C
3
!
Betrag (= Länge) eines Vektors a
x 2 + y 2 + z2
!"
!
Einheitsvektor a0
!
a
"! (Vektor durch eigene Länge)
a
!"
!
k ! a0
Vektor mit vorgegebener Länge k
! x$
! 2 : Drehung eines Vektors # & um 90°
" y%
nach links bzw. rechts
!
!
! 3 : Normalvektor zu a und b
! !
a!b
! !
a"b
! = arccos ! !
a"b
Winkel zwischen 2 Vektoren
A = a ! b ! sin " (" zwischen a und b eingeschlossen!)
Fläche Parallelogramm
Fläche Dreieck
A=
Normalabstand Punkt – Gerade ( ! 2 )
3
Normalabstand Punkt – Ebene ( ! )
Punkt = (x|y) bzw. (x|y|z)
Andere Form der HNF
!
!
Länge der Normalprojektion a auf b
Gerade
Ebene
Kreis/Kugel
" !y %
" y%
$ x ' (links) $ !x ' (rechts)
# &
# &
a ! b ! sin "
(" zwischen a und b eingeschlossen!)
2
HNF:
xn ! x + y n ! y + zn ! z " d
!
| n|
(oben steht die auf eine Seite gebrachte Geraden- bzw.
Ebenengleichung!)
!!!!!!!"
AP ! n 0
A … irgend ein Punkt auf der Geraden (bzw. Ebene)
P … Punkt, von dem man den Abstand will
n0 … Normalvektor der Geraden (bzw. Ebene)
! "!
"
a ! b0
!
X = P + s!a
!
!
X = P + s !a + t !b
!!!" 2
MX = r 2
Ellipse/Hyperbel
x2 y 2
±
=1
a2 b 2
Parabel
y 2 = 2px (rechts offen)
x 2 = 2py (oben offen)