Einführung in die Astronomie und Astrophysik I, WS 2009/10 Lösung
Werbung

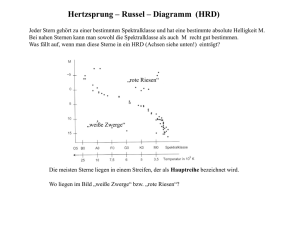
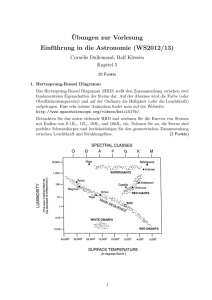
Einführung in die Astronomie und Astrophysik I, WS 2009/10 Dozenten: H. Beuther & Ch. Fendt, Tutoren: L. Burtscher & O. Porth Lösung zur 5. Übung Besprechung am 2. Dezember 2009 1 Spektrallinien a) Stärke der Spektrallinien entlang der spektralen Klassifikation Die Spektralklassen entsprechen bestimmten Oberflächentemperaturen der Sterne. Bei steigender Temperatur nimmt nicht nur die Besetzung der angeregten Zustände eines Atoms zu, sondern die Atome werden auch zunehmend ionisiert und zeigen daher nicht mehr die Spektrallinien der neutralen Atome. Das Zusammenspiel aus atomarer Anregung (Boltzmann-Faktor) und Ionisierung (Saha-Gleichung) führt zu der Beobachtung der zunächst stärker, dann schwächer werdenden Spektrallinien wenn man von einer Spektralklassen ausgehend zu “früheren” Sternen (höherer Temperatur) geht. b) Druckverbreiterung in der Sonne ∆λ ≈ Druckverbreiterung in der Hα-Linie (λ = 656.28 nm): p λ2 n · σ 2kB T /m ≈ 2.36 · 10−5 nm πc In der Sonne: Teilchenzahldichte n = 1.5 · 1023 m−3 , Streuquerschnitt σ ≈ 10−21 m2 , Temperatur T = 5777 K, Masse eines Wasserstoffatoms m = 1.7 · 10−27 kg. Die Druckverbreiterung spielt in der Sonne keine große Rolle. c) Relative Linienstärke der Calcium-II-Linie zu den Balmer-Linien in der Sonne Vergleiche die Anzahl der neutralen Wasserstoffatome im ersten angeregten Zustand (Balmer-Linien sind Übergänge auf n = 2) zur Anzahl der einfach ionisierten Calcium-Atome im Grundzustand (Calcium H- und K-Linien sind Übergänge auf n = 1). Die detaillierte Rechnung bitten wir in Carroll & Ostlie, Example 8.1.5 (Second Edition) nachzuschlagen; hier wollen wir den Lösungsweg skizzieren. Die meisten Wasserstoff-Atome in der Sonne sind nicht ionisiert, aber nur etwa 5 · 10−9 dieser Atome sind im ersten angeregten Zustand. Bei Calcium ist es umgekehrt: Es gibt viel mehr ionisierte als neutrale Calcium-Atome, aber von den ionisierten Atomen sind fast alle im Grundzustand. 1 Damit wird klar, warum die Ca-II-Linien so viel stärker sind als die Balmer-Linien: Es gibt zwar etwa 500 000 mal mehr Wasserstoff-Atome als Calcium-Atome, aber nur die wenigsten dieser WasserstoffAtome sind neutral und im Grundzustand. Wenn man alle Faktoren zusammen multipliziert erhält man den Faktor 1/395 für die Stärke der Calcium- geteilt durch die Stärke der Balmer-Linien. 2 Sternradien a) Sternradien und Leuchtkraft r R= L 1 4πσB T 2 Bei gleicher Spektralklasse (gleicher Temperatur) skaliert R ∝ also 100 Mal größer. √ L; der 10 000 mal hellere Stern ist b) Temperatur in der Sternatmosphäre Aus dem Hertzsprung-Russell-Diagramm (HRD) liest man ab, dass Spektralklasse M = ˆ T = 2000 ... 3500 K; M5 ist etwa in der Mitte dieses Bereichs bei ≈ 2700K. c) Leuchtkraftklassen Ein Helligkeitsunterschied von 10 000 entspricht einer Magnitudendifferenz von 2.5 lg 104 = 10. Blickt man auf ein Hertzsprung-Russell-Diagramm sieht man, dass, wenn der eine Stern ein Hauptreihenstern (Leuchtkraftklasse V) ist, der andere ein heller Riese (Leuchtkraftklasse II) ist. d) Temperaturen Aus dem HRD: Sterne der Spektralklasse G5 haben typischerweise eine Temperatur von 5400 K, A5 haben 8100 K. 3 Sternmassen a) Inklination Das Verhältnis der Massen im Doppelsternsystem hängt nicht von der Inklination ab, die Gesamtmasse ist ∝ 1/ cos3 i. b) Massenbestimmung mA + mB = 4π 2 · G · P2 1/p cos i 3 mB /mA = · α̃3 = 6.2 · 1030 kg ≈ 3Msun αA = 0.466 αB Die Masse von Sirius A entspricht also etwa 2 Sonnenmassen, die von Sirius B etwa einer Sonnenmasse. 2 c) Größe und Leuchtkraftklassen Mit der bekannten Entfernung und der scheinbaren Leuchtkraft kann man über den Entfernungsmodul die absolute Leuchtkraft von Sirius ausrechnen: d = 1.454.84 M = m − 5 lg 10pc FSirius /FSonne = 100(4.84−1.45)/5 = 22.7 FSiriusA /FSiriusB = 22.7/2.6% ≈ 870 Mit der Spektralklasse von Sirius (A1) kann man im HRD nachschauen und sieht dass Sirius auf der Hauptreihe liegt, sein Begleiter dagegen ein weißer Zwerg ist. 4 Rotation der Sterne a) break-up velocity Mit v 2 /R = GM/R2 folgt die aus der Vorlesung bekannte Beziehung vbreak−up ∝ p M/R. In der letzten Übung haben wir den Gesamtbahndrehimpuls aller Sonnensystemkörper zum 88 fachen des Drehimpulses der Sonne berechnet. Die Sonne dreht sich am Äquator in etwa 25 Tagen einmal um die eigene Achse und hat einen Durchmesser von 1.39 · 109 m, mithin eine Rotationsgeschwindigkeit von 2 km/s. Wäre der gesamte Bahndrehimpuls in der Sonne vereint, hätte sie eine Rotationsgeschwindigkeit von etwa 180 km/s oder ≈ 0.4 · vbreak−up . Rotationsperiode wenn der gesamte Drehimpuls des Sonnensystems in der Sonne wäre: ω = v/r = 180km/s/rSonne = 2.6 · 10−4 s−1 P = 2π ≈ 6.7h ω b) Minimale Rotationsperiode Einsetzen in obige Relation gibt für einen Stern mit 2 Sonnenmassen und 100 Sonnenradien: vbreak−up ≈ 62 km/s. c) Minimale Rotationsperiode von Sirius B Wir blicken wieder ins HRD: Die Leuchtkraft war gegeben als 2.6 % der Sonnenleuchtkraft. Mit der Spektralklasse von Sirius B (A2) können wir die Effektivtemperatur zu etwa 8000 K abschätzen (wahr: ca. 25 000 K!) und damit über Tef f = L σB 4πR2 1/4 den Radius zu etwa R ≈ 6 · 107 m ≈ 0.02 · RSonne . Der wahre Radius ist etwa 0.008 · RSonne . Der Fehler dürfte hauptsächlich aus der sehr ungenauen Temperaturbestimmung herrühren. Damit ist die maximale Rotationsgeschwindigkeit ca. 40 km/s, die minimale Rotationsperiode 880 s. 3