LU_13_loesungen

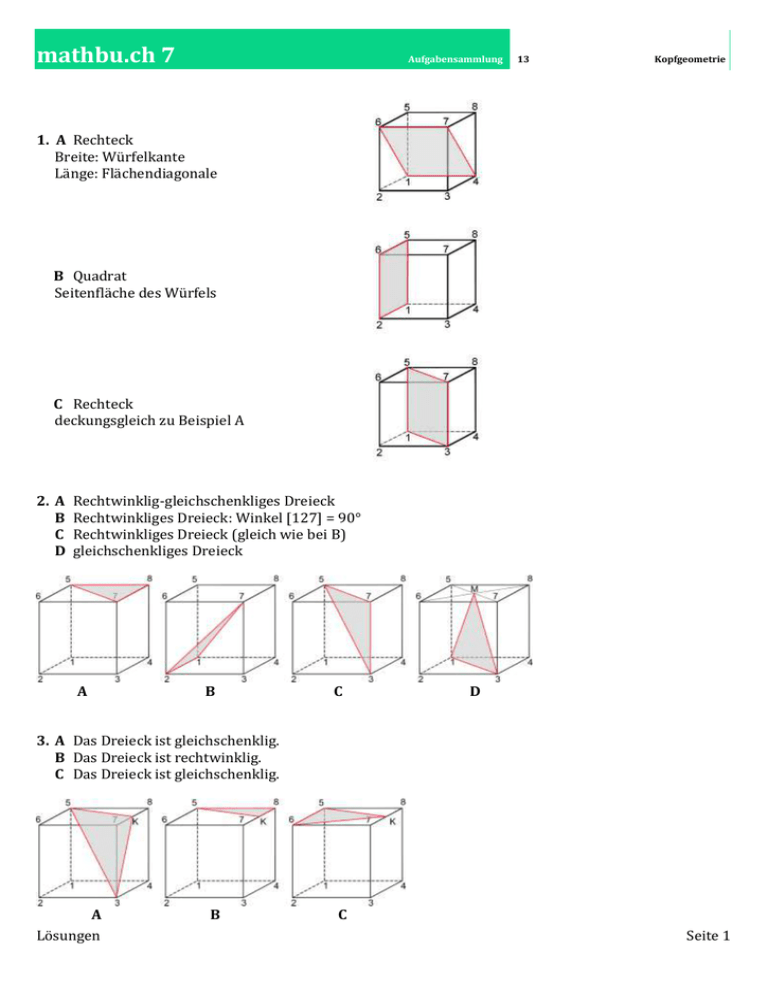
mathbu.ch 7
Aufgabensammlung
13
Kopfgeometrie
1. A Rechteck
Breite: Würfelkante
Länge: Flächendiagonale
B Quadrat
Seitenfläche des Würfels
C Rechteck
deckungsgleich zu Beispiel A
2. A
B
C
D
Rechtwinklig-gleichschenkliges Dreieck
Rechtwinkliges Dreieck: Winkel [127] = 90°
Rechtwinkliges Dreieck (gleich wie bei B)
gleichschenkliges Dreieck
A
B
C
D
3. A Das Dreieck ist gleichschenklig.
B Das Dreieck ist rechtwinklig.
C Das Dreieck ist gleichschenklig.
A
Lösungen
B
C
Seite 1
mathbu.ch 7
Aufgabensammlung
13
Kopfgeometrie
4. A Die Diagonalen stehen rechtwinklig. Es sind Quadrat-Diagonalen.
B Ja. Es sind die Diagonalen des Rechtecks [5137]
C In einem Rechteck stehen die Diagonalen nicht senkrecht aufeinander.
A
B
5. A Die Schnittfläche ist ein gleichseitiges Dreieck.
Alle Seiten sind Flächendiagonalen des Würfels.
B Die Schnittfläche ist ein Rechteck.
C Ja. Der Schnitt muss parallel zu einer Seitenfläche geführt werden.
A
B
6.
A Das Sechseck mit Diagonalen kann das Schattenbild
eines Würfels sein.
Die Raumdiagonale des Würfels steht genau senkrecht
zur Projektionsebene und das Licht fällt genau in dieser
Richtung ein.
Das Sechseck kann aber auch das Schattenbild einer
Pyramide sein.
B Das Quadrat mit Diagonalen kann das Schattenbild
einer quadratischen Pyramide sein. Beleuchtung von
oben, senkrecht zur Blattebene.
Das Schattenbild kann auch von einem regelmässigen
Oktaeder (Doppelpyramide) stammen.
Lösungen
Seite 2
mathbu.ch 7
Aufgabensammlung
13
Kopfgeometrie
7. Ja. Ein Beispiel:
Wenn man den Schnitt durch 5 und 7parallel zur Kante [26] führt, so ist die Schnittfläche ein Rechteck,
dessen kürzere Seite gleich lang wie die Würfelkante und dessen längere Seite so lang wie eine
Flächendiagonale ist.
Schneidet man immer näher bei der Kante [26], beispielsweise parallel zum Schnitt [1375], so entsteht
eine Situation, in der alle vier Rechteckseiten gleich lang werden. Die Schnittfläche ist dann ein Quadrat.
8. Das Dreieck [73D] ist rechtwinklig, und die Hypotenuse ist sicher nicht doppelt so lang wie die Kathete
[7D].
9. Das Viereck ist ein Rechteck.
Im Dreieck PQS ist die Verbindung halb so lang wie QS und parallel dazu. Das gleiche gilt auch für die
Mittenverbindung im Dreieck QRS. Zwei gegenüberliegende Seiten sind parallel und gleich lang, also liegt
sicher ein Parallelogramm vor. Weil aber auch noch die beiden Diagonalen gleich lang sind, handelt es
sich um ein Rechteck.
Lösungen
Seite 3