OPERATORENLISTE Mathematik - Christian von Mannlich

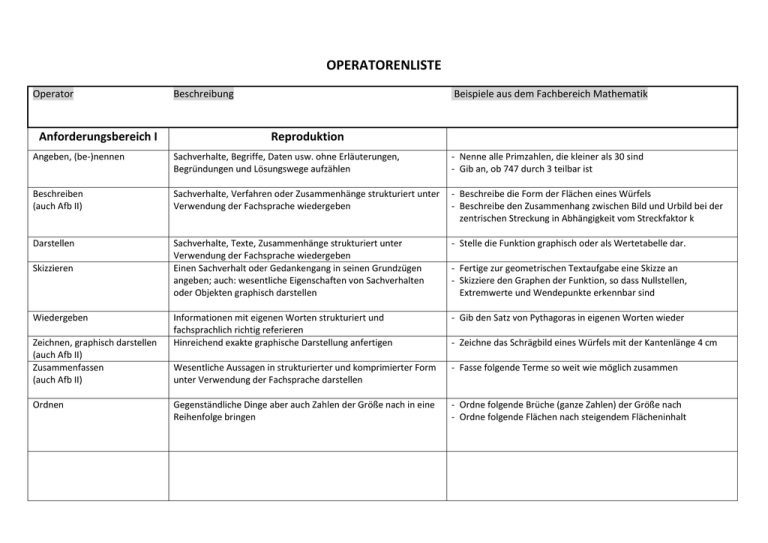
OPERATORENLISTE
Operator
Anforderungsbereich I
Beschreibung
Beispiele aus dem Fachbereich Mathematik
Reproduktion
Angeben, (be-)nennen
Sachverhalte, Begriffe, Daten usw. ohne Erläuterungen,
Begründungen und Lösungswege aufzählen
- Nenne alle Primzahlen, die kleiner als 30 sind
- Gib an, ob 747 durch 3 teilbar ist
Beschreiben
(auch Afb II)
Sachverhalte, Verfahren oder Zusammenhänge strukturiert unter
Verwendung der Fachsprache wiedergeben
- Beschreibe die Form der Flächen eines Würfels
- Beschreibe den Zusammenhang zwischen Bild und Urbild bei der
zentrischen Streckung in Abhängigkeit vom Streckfaktor k
Darstellen
Sachverhalte, Texte, Zusammenhänge strukturiert unter
Verwendung der Fachsprache wiedergeben
Einen Sachverhalt oder Gedankengang in seinen Grundzügen
angeben; auch: wesentliche Eigenschaften von Sachverhalten
oder Objekten graphisch darstellen
- Stelle die Funktion graphisch oder als Wertetabelle dar.
Informationen mit eigenen Worten strukturiert und
fachsprachlich richtig referieren
Hinreichend exakte graphische Darstellung anfertigen
- Gib den Satz von Pythagoras in eigenen Worten wieder
Wesentliche Aussagen in strukturierter und komprimierter Form
unter Verwendung der Fachsprache darstellen
- Fasse folgende Terme so weit wie möglich zusammen
Gegenständliche Dinge aber auch Zahlen der Größe nach in eine
Reihenfolge bringen
- Ordne folgende Brüche (ganze Zahlen) der Größe nach
- Ordne folgende Flächen nach steigendem Flächeninhalt
Skizzieren
Wiedergeben
Zeichnen, graphisch darstellen
(auch Afb II)
Zusammenfassen
(auch Afb II)
Ordnen
- Fertige zur geometrischen Textaufgabe eine Skizze an
- Skizziere den Graphen der Funktion, so dass Nullstellen,
Extremwerte und Wendepunkte erkennbar sind
- Zeichne das Schrägbild eines Würfels mit der Kantenlänge 4 cm
Anforderungsbereich II
Reorganisation und Transfer
Abschätzen
Durch begründete Überlegungen Größenordnungen angeben
Analysieren, untersuchen
Wichtige Bestandteile oder Eigenschaften auf eine bestimmte
Fragestellung hin herausarbeiten
Einen bekannten Zusammenhang oder eine bekannte Methode
auf einen anderen Sachverhalt beziehen
Anwenden
Begründen
Sachverhalte auf Regeln, Gesetzmäßigkeiten oder kausale
Zusammenhänge zurückführen
Beschreiben
(auch Afb I)
Bestimmen, ermitteln,
berechnen
(auch Afb III)
Sachverhalte, Verfahren oder Zusammenhänge strukturiert unter
Verwendung der Fachsprache wiedergeben
Zusammenhänge oder Ergebnisse ausgehend von einem Ansatz
oder aus einem Diagramm, Text o.a. gewinnen, den Lösungsweg
unter Angabe von Zwischenschritten darstellen und das Ergebnis
formulieren
Zu einem Sachverhalt eine selbständige und in der Sache
objektive und begründete Einschätzung nach
fachwissenschaftlichen und fachmethodischen Kriterien
formulieren
Kausale oder fachspezifische Zusammenhänge im Hinblick auf
eine gegebene Fragestellung oder Erklärungsmöglichkeit
untersuchen, abwägen und begründet darstellen.
Einen Sachverhalt auf der Grundlage differenzierter Kenntnisse
und Einsichten sprachlich angemessen (Fachsprache) und
nachvollziehbar in einen Begründungszusammenhang stellen.
Verwendung fachlicher Grundprinzipien, Modelle und
Zusammenhänge
Erklären und mit zusätzlichen Informationen und Beispielen
verdeutlichen
Sachverhalte, Probleme oder Fragestellungen nach fachlich
üblichen und sinnvollen Kriterien bearbeiten und eventuelle
Widersprüche aufdecken
Gemeinsamkeiten, Ähnlichkeiten und Unterschiede ermitteln
und sprachlich und formal angemessen darstellen, ggf.
argumentierend gewichten
Beurteilen
(auch Afb III)
Deuten, interpretieren
(auch AfB III)
Erklären
Erläutern
Untersuchen, prüfen
(auch Afb III)
Vergleichen, gegenüberstellen
Schätze, wie hoch ein Stapel 10€ Geldscheine ist, der 1 Mio Euro
wert ist.
Untersuche die Lagebeziehung der beiden Geraden zueinander.
Wende den Satz des Pythagoras zur Lösung der geometrischen
Aufgabenstellung an.
Wende das Assoziativgesetz zur Vereinfachung des Terms an.
Begründe, dass die Funktion mindestens einen Wendepunkt besitzt.
Ordne folgende Brüche der Größe nach. Begründe deine
Entscheidung.
Beschreibe die einzelnen Schritte deines Lösungswegs.
Bestimme die Anzahl der Nullstellen von f in Abhängigkeit vom
Parameter k.
Berechne den Flächeninhalt eines gleichseitigen Dreiecks mit der
Seitenlänge a.
Beurteile den vorgestellten Lösungsweg
Bestimme das Integral und interpretiere den Zahlenwert
geometrisch
Erkläre, warum die Konstruktion eines Dreiecks aus zwei Seiten und
einem (nicht eingeschlossenen) Winkel nicht eindeutig ist.
Erläutere die Aussage des Satzes anhand eines Beispiels.
Untersuche folgende Terme auf Äquivalenz.
Vergleiche die beiden Lösungswege hinsichtlich ihrer Komplexität
miteinander.
Zeichnen, graphisch darstellen
(auch Afb I)
Zeigen, nachweisen (oder
widerlegen)
(auch AfbIII)
Anforderungsbereich III
Bestimmen, ermitteln,
berechnen
(auch Afb II)
Beurteilen
(auch Afb II)
Beweisen, zeigen, nachweisen
Interpretieren
Zeigen, nachweisen (oder
widerlegen)
(auch AfbII)
Hinreichend exakte graphische Darstellung anfertigen
Aussagen oder Sachverhalte unter Nutzung geltender
Gesetzmäßigkeiten, Herleitungen und logischen Begründungen
bestätigen oder ablehnen.
Zeichne den Funktionsgraphen der Funktion f mit der
Funktionsgleichung f(x)=…
Zeige, dass bei einer durch 3 teilbaren Summe nicht zwangsläufig
jeder einzelne Summand durch 3 teilbar sein muss.
Reflexion und Problemlösung
Zusammenhänge oder Ergebnisse ausgehend von einem Ansatz
oder aus einem Diagramm, Text o.a. gewinnen, den Lösungsweg
unter Angabe von Zwischenschritten darstellen und das Ergebnis
formulieren
Zu einem Sachverhalt oder einer Aussage unter Verwendung von
Fachwissen und Fachmethoden eine begründete Einschätzung
geben
Umfangreichere Aussagen oder komplexe Sachverhalte unter
Verwendung von bekannten Sätzen und logischen
Schlussfolgerungen bestätigen
Komplexe Zusammenhänge oder Ergebnisse begründet auf eine
gegebene Fragestellung beziehen
Aussagen oder Sachverhalte unter Nutzung geltender
Gesetzmäßigkeiten, Herleitungen und logischen Begründungen
bestätigen oder ablehnen.
Bestimme in offenen Aufgabenstellungen die Lösungen.
Beurteile das beschriebene Verfahren zur näherungsweisen
Bestimmung einer Extremstelle.
Beweise den Höhensatz unter Verwendung des Satzes von
Pythagoras.
Interpretiere den Verlauf der gegebenen Füllkurve
siehe Beweisen!