E2 Klausur 2011 + Lösung
Werbung
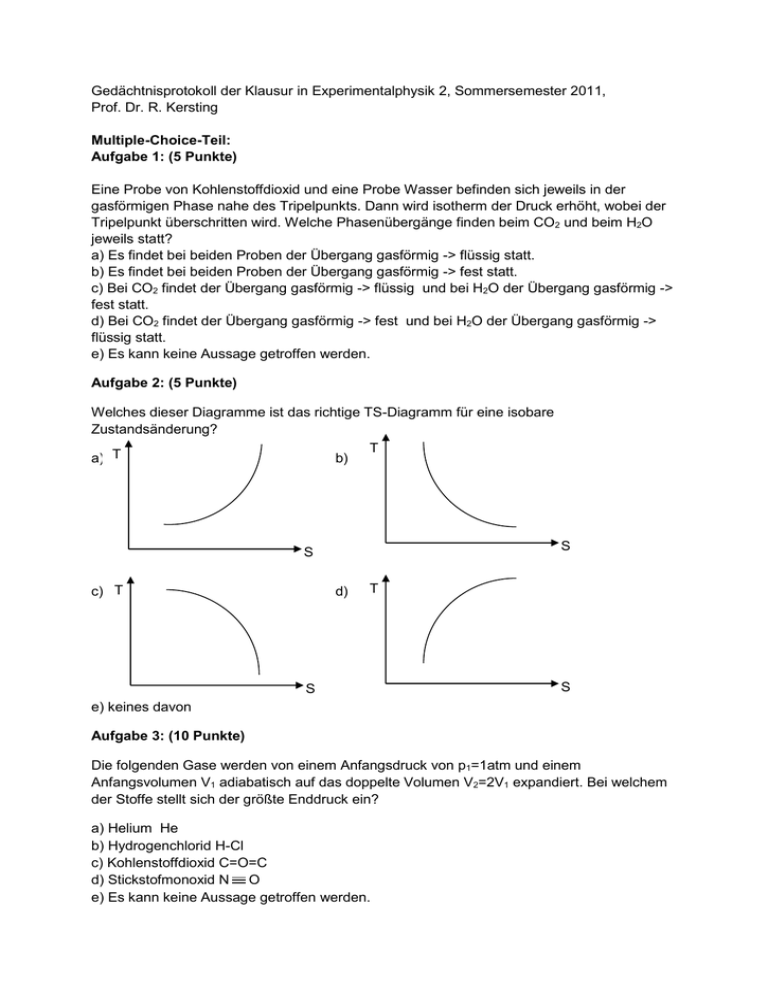
Gedächtnisprotokoll der Klausur in Experimentalphysik 2, Sommersemester 2011, Prof. Dr. R. Kersting Multiple-Choice-Teil: Aufgabe 1: (5 Punkte) Eine Probe von Kohlenstoffdioxid und eine Probe Wasser befinden sich jeweils in der gasförmigen Phase nahe des Tripelpunkts. Dann wird isotherm der Druck erhöht, wobei der Tripelpunkt überschritten wird. Welche Phasenübergänge finden beim CO2 und beim H2O jeweils statt? a) Es findet bei beiden Proben der Übergang gasförmig -> flüssig statt. b) Es findet bei beiden Proben der Übergang gasförmig -> fest statt. c) Bei CO2 findet der Übergang gasförmig -> flüssig und bei H2O der Übergang gasförmig -> fest statt. d) Bei CO2 findet der Übergang gasförmig -> fest und bei H2O der Übergang gasförmig -> flüssig statt. e) Es kann keine Aussage getroffen werden. Aufgabe 2: (5 Punkte) Welches dieser Diagramme ist das richtige TS-Diagramm für eine isobare Zustandsänderung? T a) T b) S S c) T d) T S S e) keines davon Aufgabe 3: (10 Punkte) Die folgenden Gase werden von einem Anfangsdruck von p1=1atm und einem Anfangsvolumen V1 adiabatisch auf das doppelte Volumen V2=2V1 expandiert. Bei welchem der Stoffe stellt sich der größte Enddruck ein? a) Helium He b) Hydrogenchlorid H-Cl c) Kohlenstoffdioxid C=O=C d) Stickstofmonoxid N O e) Es kann keine Aussage getroffen werden. Aufgabe 4: (10 Punkte) Zwei Kondensatoren haben die gleiche Plattenfläche und den gleichen Plattenabstand. Kondensator 1 ist mit Luft (ε=1) und Kondensator 2 ist mit einem Dielektrikum mit ε>1 gefüllt. Beide Kondensatoren werden nun mit der gleichen Spannung aufgeladen. Was gilt für die elektrischen Feldstärken E1 und E2 in den beiden Kondensatoren? a) E1 > E2 b) E1 < E2 c) E1 = E2 d) Es sind weitere Informationen nötig, um eine Aussage zu treffen. e) Alle obigen Antworten sind falsch (Anmerkung: LOL!) Aufgabe 5: (5 Punkte) Ein geladenes Teilchen befindet sich anfangs in Ruhe. Dann werden ein homogenes elektrisches und ein magnetisches Feld eingeschaltet. Die Feldlinien des E-Feldes und des B-Feldes verlaufen parallel. Auf welcher Bahn bewegt sich das Teilchen? a) Auf einer Parabel b) Auf einer Gerade c) Auf einer Kreisbahn d) Auf einer Spirale e) nichts von dem, oder was anderes, oder uns fiel nichts mehr ein aber wir haben uns eingebildet es müsste 5 Antwortmöglichkeiten geben. Aufgabe 6: (5 Punkte) Die Abbildung zeigt eine Spule mit der Induktivität L, der Pfeil deutet die Richtung der Induktionsspannung Uind. an. Was folgt daraus für den Stromfluss durch die Spule? a) Der Stromfluss ist abnehmend und nach rechts. b) Der Stromfluss ist konstant und nach links. c) Der Stromfluss ist abnehmend und nach links. d) Der Stromfluss ist zunehmend und nach rechts. e) Es kann keine Aussage getroffen werden. Aufgabe 7: (10 Punkte) Ein Eisblock von 900g befindet sich auf einer Temperatur von -10°C. Es wird nun eine Wärmemenge von 140kJ zugeführt. Wie viel Gramm des Eisblocks verbleiben im festen Zustand? Wärmekapazität von Eis: 2,33 kJ/kgK Spezifische Schmelzwärme von Wasser: 333kJ/kg Aufgabe 8: (10 Punkte) Ein Mol eines idealen Gases befindet sich in der linken Hälfte eines Behälters und kann wegen einer Trennwand nicht in die rechte Hälfte gelangen. Dann wird die Trennwand herausgezogen, danach befinden sich die Teilchen im gesamten Behälter. Der Behälter ist thermisch isoliert. Berechnen Sie die Entropieänderung bei diesem Vorgang! Aufgabe 9: (10 Punkte) Ein Stab, dessen linke Hälfte aus Kupfer und dessen rechte Hälfte aus Aluminium besteht, wird mit Hilfe zweier Wärmereservoire auf konstanter Temperatur gehalten: Links auf T 1 = 100°C und rechts auf T2 = 0°C. Berechnen Sie die Temperatur TG an der Grenzfläche der beiden Metalle. Wärmeleitfähigkeiten: Aluminium: 236W/m*K Kupfer: 420 W/m*K Aufgabe 10: (10 Punkte) Ein Kondensator der Kapazität C ist anfangs mit der Ladung Q0 geladen, zum Zeitpunkt t=0 wird ein Schalter geöffnet so dass der Kondensator über den Widerstand R entladen wird. Leiten Sie die Differentialgleichung für diesen Vorgang her und die Lösung Q(t) = Q0 e-t/RC Aufgabe 11: (10 Punkte) Berechnen Sie die Impedanz, also den Betrag des komplexen Widerstandes des nebenstehenden RCL-Kreises, wenn er bei einer Frequenz f=1000Hz betrieben wird. R Anmerkung: Es waren noch irgendwelche Werte für R, C, L gegeben, aber egal. Aufgabe 12: (10 Punkte) Ein unendlich langer, dünner gerader Leiter wird von einem Strom I durchflossen, wobei dI/dt = 1 A/s ist. Im Abstand b=1cm befindet sich eine quadratische Leiterschleife mit der Seitenlänge b. Berechnen Sie die induzierte Spannung in der Leiterschleife. Lösungen: Aufgabe 1: d) (s. Phasendiagramme) Aufgabe 2: a) S(T) = c1ln(T) + c2 also ist die Umkehrung T(S) eine e-Funktion. Aufgabe 3: c) Das Molekül CO2 hat 3 Freiheitsgrade der Translation und 2 der Rotation (Linear!), also bleiben 9-5=4 Schwingungsgrade die doppelt zählen, also insgesamt 13. Damit ist der Adiabatenexponent mit 15/13 am kleinsten und der Enddruck nach p*Vk=const. am größten. Aufgabe 4: c) Aufgabe 5: b) Magnetisches Feld hat keine Auswirkung da v parallel zu B ist. Aufgabe 6: a) Uind ist proportional zur negativen Änderung von I Aufgabe 7: Zunächst muss man den Eisblock auf 0°C erwärmen, wozu eine Wärmemenge von Q = 0,9kg * ceis * 10K nötig ist. Es verbleiben Q' = 119 kJ zum Schmelzen und damit können 357 Gramm geschmolzen werden, womit 543 Gramm übrig bleiben. Aufgabe 8: Wir könnten entweder über die Formel dS=dQ/T einen reversiblen (isothermen) Ersatzprozess betrachten und integrieren, oder noch einfacher: Anfangs kann jedes Molekül sich nur in der linken Hälfte befinden, danach im doppelten Volumen. Wir haben die Formel S=kB * ln(W) wo hier W proportional zum möglichen Volumen ist. Und wir haben NA Moleküle also deltaS = NA * kB * ln(2V/V) = R * ln2 = 5,76 J/K Aufgabe 9: Der Wärmestrom ist konstant und stetig durch die beiden Metalle also λCu * (T1 – TG) * A/L = λAl * (TG – T2) * A/L => TG = (λCuT1 + λAlT2)/(λAl +λCu) = 64°C Aufgabe 10: Nach Kirchhoff' scher Maschenregel gilt UC - UR = 0 also Q(t)/C – R*I(t) = 0. Da I die zeitliche Ableitung von Q ist haben wir eine einfache Differentialgleichung deren Lösung intelligenterweise schon gegeben ist, also einfach einsetzen und sehen: Aha, es löst die Gleichung. Aufgabe 11: ω = 2πf Zges. = R + (1/iωL + iωC)-1 Re(Z) = R ; Im(Z) = -(ωC – ωL)-1 (weil 1/i = -i) => Impedanz |Z| = (Re(Z)2 + (Im(Z)²)-0,5 = (R² + (ωC-ωL)-2)0,5 Aufgabe 12: Magnetfeld: ∫ B ds = µ0 * I , integriere kreisförmig um den Leiter im Abstand r => B(r)= µ0 I / 2πr magnetischer Fluss: Φm = ∫ B dA = b * ∫ B(r) dr = b * µ0 I /2π ∫1/r dr = bµ0I / 2π * ln(2b/b) Es ändert sich nur I, also setzen wir ins Induktionsgesetz ein und erhalten: |Uind |= dΦm/dt = bµ0 * ln2 /2π * dI/dt Einsetzen und ausrechnen: U = 1,4 * 10-8V