Lindner

274
18.2 Erster Hauptsatz der Wärmelehre
Al man erkannt hatte, daß die Wärme eine Energieform darstellt, konnte man einen allgemeinen Energieerhaltungssatz aufsteHen. Der 1. Hauptsatz der Wärmelehre beinhaltet das
Prinzip von der Erhaltung der Energie unter Einbeziehung der Wärme, und so lautet eme
er te Formulierung:
1. Hauptsatz:
In einem abgeschlossenen System bleibt die Summe aller Energien konstant.
Dabei werden alle Energieformen wie mechani che Energie Wärme, Elektroenergie usw.
einbezogen.
Eine zweite Formulierung lautet:
1. Hauptsatz:
E gibt kein Perpetunm mobile 1. Art.
Da. heißt, e gibt keine Maschine, die Arbeit verrichtet ohne daß ein ent prechender Betrag
an Energie zugeführt wird.
Für eine dritte Formulierung, die sich mathemati ch fa en läßt, muß eine neue Größe, die
innere Energie V eine System, eingeführt werden:
Die innere Energie i t der ge amte Energieinhalt eines System, z. B.einer be timmten
Menge Ga . Sie i t eine Zustand größe und wird für eine gegebene Menge Ga durch die
Zu tand größen Temperatur, Druck und Volumen bestimmt.
Die innere Energie eine Systems kann ich entsprechend dem Satz von der Erhaltung der
Gesamtenergie nur durch Energieaustausch mit der Umgebung in Fonn von Wärme oder
durch die Verrichtung von Arbeit ändern.
Im Bereich der Wärmelehre geht e um die Zufuhr oder Ableitung von Wärme und die
vom Sy tern oder am Sy tem verrichtete Arbeit. Der 1. Hauptsatz kann nun als Bilanz
die er Größen dargestellt werden.
Die dritte Formulierung des 1. Haupt atze lautet daher:
I ßU = Q+ W I
1. Haupt atz
(18.6)
Die Änderung der inneren Energie i t gleich der Summe von zu- oder abgeführter Wärme
und verrichteter Arbeit.
Für die Bilanz von Energie und Arbeit gilt folgende Vereinbarung:
Jede dem y tem zugeführte Energie oder Arbeit wird positiv, und jede abgegebene Energie oder Arbeit wird negativ gezählt.
In differentiel1er Form gilt für die Änderung der inneren Energie U:
IdU = dQ +dW I
1. Hauptsatz
(18.7)
18.2
Er ter Hauptsatz der Wärmelehre
275
Q be chreibt den Wämleau tau ch mit der Umgebung und W die am Sy tern oder vom
Sy tern errichtete Arbeit. E ind Prozeßgrößen ie werden vom konkreten Prozeßverlauf
be timmt. Dagegen i t U eine Zustand größe., die den jeweiligen Zustand des Sy tems
beschreibt, unabhängig vom Weg zu diesem Zustand.
Die vom Ga abgegebene Arbeit kann z. B. darin be tehen, daß es ich bei konstant bleibendem Druck p au dehnt a1 0 ein Volumen V um l:!:.. V vergrößert Man denke dabei
an irgendeine Wärmekraftmaschine bei der auf die eWei e ein Kolben hin- und herbewegt wird. Die Arb it W wird dann durch das Produkt aus der vom Ga auf den Kolben
wirkenden Kraft F und dem om Kolben zurückgelegten Weg s gegeben. Hat der Kolben
den Querschnitt A und da im Zylinder einge ehIo ene Gas den Druck p, 0 ist die Kraft
gl,eich dem Produkt pA und die Arbeit W = pAs. Nun i t As da während der Bewegung
vom Kolben verdrängte Volumen D.. V, 0 daß gilt W = Pß. V. Es ist jedoch zu bedenken,
daß die auf den Kolben wirkende Kraft F und damit auch der Druek p beim Zurücklegen
des Wege s nicht konstant bleibt.
dW
i
p.
dV
p(V)
w
Bild 18.4: Volumenarbeit
Bild 18.3: Arbeit bei kleiner Volumenänderung
Es ist daher zunäch t von einer äußerst kleinen Volumenänderung d V au zugehen. Dann
ist die nach außen abgegebene Volurnen- oder Ausdehnung arbeit (Bild 18.3):
V2
!dW=-PdV!
bzw.
W= - !PdV
Volumenarbeit
(18.8)
VI
Trägt man den Verlauf de Druckes über dem Volumen auf (p V -Diagramm), 0 ent pricht
die Fläche unter der Kurve dem Betrag der Arbeit! Im Bild 18.4 i teine Kompre Ion
dargestellt. Dem Sy tern wird Arbeit zugeführt ie i t po itiv.
Mit 18.7 erhält man den 1. Haupt atz für Ga e:
!
dU = dQ - pdV
I
(18.9)
Die Änderung der inneren Energie eine Ga e ergibt ich omit au der zu- bzw. abgeführten Wärmemenge und der am Ga oder vom Ga verrichteten Volumenarbeit.
276
19 Zustandsänderungen idealer Gase
19 Zustandsänderungen idealer Gase
E wurde bereits in Abschnitt 17.4 dargestellt, daß der Zustand einer bestimmten Menge Ga durch die drei Zustandsgrößen Druck, Volumen und Temperatur beschrieben wird.
Die Zu tand gleichung (17.22) gibt den Zusammenhang zwischen diesen Größen an. Ein
gegebener Zu tand läßt ich auf verschiedene Weise ändern. So kann z. B. das Gas zuammengepreßt werden, wodurch sein Volumen kleiner wird und die Temperatur ansteigt.
Eben 0 verschieben sich die Werte p, V und T, wenn das Gas erwärmt wird. In welcher
Weise hierbei in be ondere Druck und Volumen zusammenhängen, läßt sich mittels eines
Diagramms veran chaulichen, de sen Ab zisse das Volumen V und dessen Ordinate den
Druck p einer be timmten Ga menge darstellt (p, V -Diagramm, z. B. Bild 19.1).
t
Isobare
Bild 19.1: Die vier Zustandsänderungen
Neben den speziellen Zustand änderungen, bei denen eine der drei Zustandsgrößen konstant bleibt, i ochor bei kon tantem Volumen, isobar bei konstantem Druck und isotherm
bei kon tanter Temperatur, ist noch die Zustandsänderung wichtig, bei der kein Wärmeau tau ch mit der Umgebung stattfindet. Bei ~Q = 0 spricht man von adiabatischer Zutand änderung, dabei ändern ich alle drei Zustand größen p, V und T. Im Bild 19.1 sind
die vier genannten Zustand änderungen im p, V -Diagramm dargestellt.
19.1
I ochore Zustandsänderung
Wir betrachten zuer t den Vorgang mit kon tantem Volumen:
Dem in einem fe ten Behälter eingeschlo enen Gas werde die Wärmemenge d Q zugeführt. Dann kann da Ga keine Arbeit verrichten, da die Volumenänderung d V = 0 ist und
demzufolge auch das Glied p dV ver chwindet.
Somit verbleibt au dem 1. Haupt atz (18.9)
dQ =dU
Die zugeführte Wärmemenge dQ kann hier a1 0 allein dazu führen, die Temperatur des
Ga e zu erhöhen. Die geht nach der Gleichung (18.1) vor sich, so daß
I dU = mevdT
bzw.
~U =
mev ~T
Änderung der
inneren Energie
(19.1)
19.2
Isobare Zustandsänderung
277
wird. Hierin kommt zum Ausdruck, daß die innere Energie nur von der Temperatur abhängt, da mund Cv konstante Größen sind. Außerdem läßt es sich experimentell beweisen,
daß die innere Energie U vom Volumen unabhängig ist.
.- ...... ----
.....
_
.....
----_ ......
-
Bild 19.2: Versuch von GAY-LUSSAC
Um dies zu bestätigen, hat GAy-LuSSAC folgenden berühmt gewordenen Versuch gemacht:
Ein luftgefülltes und ein luftleeres Gefäß stehen nebeneinander in einem Kalorimeter (Bild
19.2). Wird der beide Gefäße verbindende Hahn geöffnet, so strömt die Luft in das Vakuum
über. Hierbei wird ganz offenkundig keine Arbeit nach außen abgegeben. Vor allem zeigt
sich, daß im Kalorimeter keine Temperaturänderung eintritt und das Gas auch keine Wärme
aufnimmt oder abgibt. In Gleichung (18.7) nehmen also die GrößendQ und dW den Wert 0
an. Daher muß auch die Änderung der inneren Energie dU gleich null sein, wa wiederum
besagt, daß die innere Energie U konstant geblieben ist.
Die innere Energie des idealen Gases ist vom Volumen unabhängig und wird
allein von der Temperatur bestimmt.
Zur praktischen Durchführung des Versuches dienen zweckmäßigerwei e je eine gut
wärmeisolierte gefüllte und eine leere Druckgasflasche. Werden nach dem Überströmen
die Temperaturen gemessen, so ist die der anfangs vollen Flasche um einige Grade gesunken und die der anfangs leeren Flasche um den gleichen Betrag gestiegen. Der gesamte
Wärmeinhalt und damit U bleibt also konstant.
Nachzutragen bleibt, daß sich bei Erwärmung bei konstantem Volumen ent prechend Gleichung (17.15) der Druck erhöht:
P2
= PI'
T2
Tl
19.2 Isobare Zustandsänderung
Auch bei einer isobaren Zustandsänderung wird einem Gas Wärme zugeführt, wobei sich
seine Temperatur erhöht. Jedoch muß im Gegensatz zur isochoren Änderung dafür gesorgt werden, daß sein Druck dabei konstant bleibt. Das ist wenigsten theoreti ch möglich, wenn es in einen Zylinder eingeschlossen wird, in dem sich ein Kolben reibungslo
19 Zustandsänderungen idealer Gase
278
auf und ab bewegen kann. Denkt man sich dabei den Kolben noch massel os, so wird er
auch der geringsten Druckänderung nachgeben, damit der Druck im Innern des Zylinders
unverändert gleich dem Außendruck (äußerer Druck, Luftdruck) bleibt.
Für diesen Fall läßt sich aber die zugeführte Wärme sofort angeben. Mit der spezifischen
Wärmekapazität c p bei konstantem Druck wird in der zuletzt dargestellten Form (18.9) des
1. Hauptsatzes der Term dQ = mCpdT, und es folgt mit (19.1)
mCpdT
= mcvdT + p dV
oder auch
m(c p - cv) dT = pdV
Da alle neben den Differentialen dT und d V stehenden Faktoren konstante Größen sind,
ergibt ich nach beiderseitiger Integration
m(c p
cv)T =
-
pV
Ein Vergleich mit der Zustandsgleichung (17.23) eines idealen Gases läßt die wichtige
Beziehung erkennen:
I cp -
Cv
=
(19.2)
Rs
Sie besagt:
Die Differenz der spezifischen Wärmekapazitäten eines idealen Gases ist gleich
der speziellen Gaskonstanten.
Umgerechnet auf die molaren Wärmekapazitäten idealer Gase ergibt sich aus (19.2):
I Cm,p -
Cm, V
=
R
I
(19.3)
Da bedeutet, daß die Differenz der molaren Wärmekapazitäten idealer Gase gleich der
allgemei nen Ga konstanten ist.
a)
"
U
...............
Bild 19.3: Spezifische Wärmekapazität eines Gases bei
a) konstantem Volumen,
b) konstantem Druck
279
Cp muß de wegen größer sein al Cl'. weil da bei konstantem Druck erwärmte Gas eine
Arbeit hervorbringt (Bild 19.3). Die Differenz c p - Cv stellt damit eine Arbeit je Masse
und Temperaturänderung eines idealen Gases bei konstantem Druck dar. Daher hat auch
die Ga konstante Rs die Einheit einer Arbeit je Kilogramm und Kelvin. Werden für ein
bestimmtes Gas die Werte der spezifi ehen Wännekapazitäten in (19.2) einge etzt, so ergibt
sich beispielswei e für Wasser toff Rs = (14 235 - 10 111) J/ (kg K) = 4 124 J / (kgK) in
Überein timmung mit der Zahlentafel für Gase in 17.4.2.
Bei einer Volumenänderung von VI auf V2 ist die vom Gas bzw. am Ga i obar verrichtete
Arbeit
f
V"I
W
=-
pdV
= P(VI
- V2)
= mRs{TI
- T2) = nR<T! - Tl)
(19.4)
VI
Bei isobaren Vorgängen wird gern eine weitere Zustandsgröße die Enthalpie H. verwendet:
H
=
U+pV
Enthalpie
(19.5)
Die Enthalpie i teine Energiegröße die außer der inneren Energie die Verdrängung arbeit
p V bei konstantem Druck enthält man pricht auch om Wärmeinhalt. Au dem 1. Hauptatz für kontanten Druck folgt:
dQ = dU
+ pdV = d(U + pV) = dH
d. h., bei konstantem Dnlck ist die zugeführte Wärmemenge gleich der Zunahme der Enthalpie. Bei Pha enumwandlungen, die mei tens isobar erfolgen, wird daher häufig nicht
die Umwandlung energie, ondern die Umwandlungsenthalpie angegeben. So i t in der
Verdampfung enthalpie nicht nur die Energie zum Aufspalten der M lekül indungen, ondem auch die gelei tete Au dehnung arbeit enthalten (s. auch Kapitel 23 zu Änderungen
des Aggregatzu tande ).
19.3
Isotherme Zustandsänderung
Wir denken un jetzt da Ga in einem Zylinder einge chJo en, des en Vt lumen ich mit
Hilfe eines dicht chließenden, reibungslos bewegJjchen Kolben nach Belieben vergrößern
oder verkleinern läßt. Damit wird ich der Druck im Zylinder gegenläufig ändern. E ei
aber verlangt daß der Vorgang isotherm verlaufen, d. h. ,daß ich das Ga dabei weder erwärmen noch abkühlen oll. Da läßt ich zwar prakti eh nie ganz verhindern. doch können
wir uns vorsteHen, daß der umhüllende Zylinder 0 gut wärmeleitend i t, daß·die gebildete
Wärme ofort abfließt. Auch das den Zylinder umgebende Wärmere ervoir darf eine Temperatur dabei nicht ändern e muß a1 0 unendlich groß gedacht werden. Schließlich darf
der Vorgang nur ehr lang am erlaufen, damit genügend Zeit fur den Wärmeau tau ch
zur Verfügung teht. Kurzum: Während eine treng i otherm verlaufenden ProZC. e. muß
19
280
Zustandsänderungen idealer Gase
in jedem Augenblick ein Gleichgewichtszustand zwischen dem Gas und einer Umgebung
bestehen. Derartige Zustandsänderungen bezeichnet man daher als quasistatisch.
Da nun die Temperaturänderung dT gleich null sein soll, entfällt jetzt das in der Gleichung
(18.9) des 1. Hauptsatzes stehende Glied dU = mcvdT. Die innere Energie U muß also
während des Vorganges konstant bleiben:
Die innere Energie eines Gases ändert sich bei isothermer Volumenänderung
nicht.
Es verbleibt allein die Gleichung
dQ = pdV
Sie besagt, daß die beim Zusammendrücken des Gases aufgewandte Arbeit pd V in Form
von Wärme nach außen hin abgegeben werden muß bzw. die zur Ausdehnung erforderliche
Arbeit in Form von Wärme von außen her zuzuführen ist. Das Gas selbst darf jedenfalls
eine Temperatur nicht ändern.
Bei kon tanter Temperatur gilt jedoch das Gesetz von BOYLE-MARIOTTE (9.7), demzufolge das Produkt au Druck und Volumen eines ein ge chlossenen Gases bei konstanter
Temperatur stets den gleichen Wert haben muß.
V---I~-
Bild 19.4: Isothermen des idealen Ga es mit
Tl < T2 < T3'"
Werden die jeweil zusammengehörenden Werte von Druck und Volumen in dem p, VDiagramm eingetragen, so liegen sie alle auf einer Kurve (Bild 19.4). Sie stellt geometrisch
eine Hyperbel dar.
Diese eine Hyperbel entspricht einer bestimmten, festliegenden Temperatur TI. Sie heißt
kurz eine Isotherme. Die ganze Fläche des Diagramms kann man mit einer Schar von
Isothermen überdecken, die nach rechts oben immer höheren Temperaturen entsprechen.
I p V = const. I
Gleichung der Isotherme
eines idealen Gases
(19.6)
19.3
281
Nun oll die Volumenarbeit (18. ) bei einer i othermen Zu tand änderung berechnet werden. Da p von V abhängt. muß p durch V au gedrückt werden. Die er Zu ammenhang i t
nach der Zu tand gleichung (17.23) gegeben. Ihr zufolge ist
mRsT
p=
V
Bezeichnet VI da Anfang - und V2 das Endvolumen, so ist die gesamte aufzuwendende
Arbeit gleich
f
v.,
w=-
mRsT
dV
V
VI
Dies gibt integriert
VI
W=mRsTlnV2
Isotherme Volumenarbeit
(19.7)
Ist das Anfang volumen Vl größer als da Endvolumen V2, so wird W positiv und teUt die
bei der Kompression aufzuwendende Arbeit dar. Für den Fall dagegen, daß V2 > VI ist
handelt es ich um die Entspannung eine komprimierten Ga e . W wird dann negativ und
gibt die vom Gas gelieferte Arbeit an.
v--
Bild 19.5: I otherme Volumenarbeit
Im Diagramm (Bild 19.5) teIlt pd V ein chmale Rechteck von der Breite d V und der
Höhe p dar. Die ge amte Arbeit i t dann gekennzeichnet durch den Flächeninhalt unter der
Iotherme zwi chen den Werten VI und V2. Sie kann al 0 auch mit Millimeterpapier oder
Planimeter gemessen werden (bei Berück ichtigung der Maß tab faktoren).
Die i otherme Volumenarbeit läßt sich auch bei bekanntem Anfang druck P I und Enddruck
P2 berechnen: Nach dem Gesetz von BOYLE-MARIOTTE (9.7) ind bei kon tanter Temperatur der Druck p und das Volumen V einander umgekehrt proportional, und au (19.7)
wird
P2
W=mRsTlnPI
Isotherme Volumenarbeit
09.8)
282
Schließlich i t für den hier betrachteten Fall eine isothermen Vorgange das Produkt m Rs T
konstant und gleich p V , wobei für die es Produkt entweder der Anfang zustand p I V I oder
auch der Endzustand P2 V2 eingesetzt werden darf, so daß gegebenenfall (19.7) und (19.8)
je zwei weitere Gleichungen folgen.
In der technischen Praxis spielen sich isotherme Vorgänge näherungswei e in allen Luftkompres oren und Gasverdichtern ab. Die nach den Gleichungen (19.7) und (19.8) hierbei entstehende Wärme wird durch intensive Luft- oder Wasserkühlung abgeführt, wodurch erreicht wird, daß die Arbeitstemperatur einer solchen Ma chine im zeitlichen Mi ttel
konstant bleibt. Somit stellt ein komprimiertes Ga selbst keinen Energie peicher dar. Die
beim Komprimieren aufgewandte Arbeit wird in Form von Wärme nach außen abgegeben,
und die bei der i othermen Entspannung (z. B. von Druckluftwerkzeugen) gelieferte Arbeit
stammt dabei nur insofern aus dem Gas, als es sich dabei selb t und seine Umgebung stark
abkühlt.
Beispiel:
Welche Arbeit i t aufzuwenden, um einen Luftreifen von 5 I Fa sung vermögen bei Normalluftdruck
auf 0,3 MPa Überdruck i otherm aufzupumpen, und welche Wärmemenge gibt die komprimierte Luft
dabei nach außen ab?
E ist der Anfangsdruck PI = 101,3 kPa, der Enddruck P2
nicht gegeben. Aus (19.8) folgt mit mRS T = P2 V2
t l 1 P2
W = P2 Y2 n -
PI
= 4,013 . 10
5
= 401, 3 kPa,
N .5.10- 3 m 3 I 401 , 3
n
m2
101 , 3
V2
= 0,005 m 3 . VI
ist
= 2 760 Nm = 2. 8 k1
Das positive Vorzeichen gibt an daß Arbeit vom Betrag 2,8 kJ aufzuwenden ist; diese 2,8 kJ gibt die
Luft al Wärme an die Umgebung ab.
19.4 Adiabatische Zustandsänderung
Wird dafür ge orgt, daß während der Volumenänderung des Gases kein Wärmeaustausch
mit der Umgebung tattfinden kann, so nennt man dies einen adiabatischen Vorgang. Wir
können uns den Zylinder mit einer vollkommen wärmedichten Umhüllung versehen vorteHen (Bild 19.6). Doch die beste Dämmscmcht wird stets ein wenig Wärme durchlassen.
Wenn die Verdichtung sehr rasch verläuft, verbleibt keine Zeit zum Wärmeaustau ch, und
die gesamte bei der Verdichtung entstehende Wärme bleibt im Gas enthalten.
E können sich sehr hohe Temperaturen entwickeln, die zur Entzündung brennbarer Stoffe
führen (Dieselmotor). Auch bei den sehr ra chen Druckschwankungen in den Schallwellen
handelt e sich um rein adiabatische Vorgänge.
Um die hierfür gültigen Ge etzmäßigkeiten zu finden, gehen wir wieder vom 1. Hauptsatz
dQ = mcvdT + p dV aus und beachten, daß bei einem adiabatischen Vorgang Wärme
weder zu- noch abgeführt wird. Infolgedessen ist dQ = 0, und der 1. Hauptsatz geht in die
Gleichung über:
dU
= -pdV = dW
mit
dU
= mcvdT
Bei adiabatischer Zustandsänderung eines idealen Gases wird die Volumenarbeit auf Kosten der inneren Energie verrichtet.
19.4
Adiabati che Zustandsänderung
283
Bild 19.6: Bei adiabatischer Verdichtung steigen Druck und Temperatur
:::: : :L:~~: : :
..........................
.............
......
.....
......
, .... .
•
••••
Führen wir noch den Druck p =
0
••
,
'"
••••
m~sT
aus der Zustandsgleichung (17.23) ein, so folgt
dV
-mcvdT = mRsTV
Diese Gleichung kann beiderseits integriert werden, wobei nach (19.2) Rs
gesetzt wird:
Cp -
Cv
Das ergibt dann
Cv
in -Tl = (c p
T2
-
cv) In -V2
VI
oder
(TT21 ) CV
__
P
(V2])C-CV
V
Es ist ferner allgemein üblich, das Verhältnis der beiden spezifischen Wärmekapazitäten
ais Adiabatenexponenten K (sprich: kappa) abzukürzen:
~
~
Adiabatenexponent
(19.9)
Mit diesem Adiabatenexponenten folgt
Temperatur-Volumen-Beziehung
bei adiabatischer Zustandsänderung
Nun ist nach der Zustandsgleichung (17.16)
oder
(19.10)
284
19 Zustandsänderungen idealer Gase
Dies, in (19.10) eingesetzt, ergibt
Tl
T2
)K-l
(T2)K-l
P2
Tl
= (PI
oder
Temperatur-Druck-Beziehung bei
adiabatischer Zustandsänderung
(19.11)
Durch Gleichsetzen der rechten Seiten von (19.10) und (19.11) folgt
Druck-Volumen-Beziehung bei
adiabatischer Zustandsänderung
(19.12)
bzw . das Poissonsche Gesetz:
I.
PVK
= const.
Gleichung der Adiabaten
eines idealen Gases
(19.13)
f
P2/
J
---i---~~---.
V
Bild ] 9.7: P, V-Diagramm für adiabatische
und isotherme Kompression: P2i < P2a
---I~~
Die Gleichungen (19, lO) bis (19.13) werden die Poissonschen Gleichungen genannt. Wird
eine o1che Adiabate in das p,V -Diagramm eingezeichnet, so ist zu sehen, daß sie steiler
al eine Isotherme verläuft (Bild 19.7). Dies ist deshalb leicht einzusehen, weil z. B. bei
Kompre ion die gebildete Wärme im Gas enthalten bleibt und damit der Druck schneller
an teigen muß als bei i othenner Verdichtung.
Beispiele:
I. Da in früheren Zeiten benutzte pneumatische Feuerzeug bestand aus einem MetaHzylinder, in
den ein dicht chließender Kolben rasch hineingestoßen wurde. Dadurch kam ein Stückchen Feuerchwamm zum Glimmen. Die Anfangstemperatur sei 20 oe, das Volumen werde auf 1120 verringert.
Welche Temperatur ent teht?
Nach ( 19.10) i t
)K-J bzw.
v~
V
T2 = Tl (
T2
= 293 K (
1 ) t ,4-1
1/20
= 293 K . 20°,4 =
971 K;
f}2
= 698 oe
19.5
Polytrope Zustandsänderung
285
2. Im Dieselmotor wird die hohe Zündtemperatur im Zylinder durch adiabatische Kompression der
angesaugten Luft erreicht. Welche Temperatur entsteht bei einer Anfangstemperatur von 25 oe und
einem Anfangsdruck von 1 bar, wenn ein Enddruck von 38 bar erreicht wird?
Nach (19.11) ist
T2
=
K-l
(~~)
Tl
ß2 = 570,4
-K-
= 298 K . 38°,286 =
843,3 K;
oe
Die Volumenarbeit bei der adiabatischen Zustandsänderung kann bei Kenntnis der Anfangs- und Endtemperatur leicht angegeben werden: Die bereits angegebene, aus dem ersten Hauptsatz folgende Gleichung
= mev dT
dW
liefert, zwischen den Grenzen Tl und T2 integriert,
IW =
mev (T2 - TJ)
I
Volumenarbeit bei
adiabatischer Zustandsänderung
(19.14)
Da beispielsweise bei der Kompression T2 > Tl gilt, ergibt sich für die Arbeit Wein positiver Wert, wie es auch der in Abschnitt 18.2 getroffenen Vorzeichenvereinbarung ent pricht.
Unter Verwendung der Beziehung dW = - pd V und der POISSONschen Gleichung (19.12)
ergibt sich für die Volumen arbeit bei adiabatischer Zustandsänderung der folgende Au druck:
W
=
PI v1
K
-1
[(V)K-t -1 ]
_1
V2
(19.15)
19.5 Polytrope Zustandsänderung
Isotherme und adiabatische Zustandsänderung sind ideale Grenzfälle, die ich in reiner
Form technisch nicht verwirklichen lassen. Weder ist es möglich, die Arbeitstemperatur
eines Gases genau konstant zu halten, noch kann man den Zu- oder Abfluß von Wärme
vollständig verhindern. Der Realfall ist zwischen diesen beiden idealen Grenzfällen zu vermuten. Wird allgemein K durch den Polytropenexponenten n er etzt und dafür ein Wert
angenommen, der (für Luft) zwischen 1 und 1,4 liegt - etwa 1,2 oder 1,3 -, so geben die
Gleichungen (19.10) bis (19.13) die wirklichen Verhältnisse einigermaßen richtig wieder.
Eine Zustandsänderung, die weder isotherm noch adiabatisch verläuft, heißt polytrop. Die
entsprechend geänderte Gleichung (J 9.13) lautet dann
I pV
Cl
n
=
const.
< n < K)
!
Gleichung der Polytrope
eines idealen Gases
(19.16)
21
302
Kreisprozesse und zweiter Haupt atz der Wärmelehre
Im Zeitraum dt legt das Molekül eine Strecke v dt zurück. Dann i t die Strecke zwi chen
vdt
v
= - .. Diese Strecke I heißt
dN
N
zwei Zu ammenstößen im Durchschnitt gleich 1
1=
(20.29)
Mittlere freie Weglänge
N
rc.J2d 2 -
V
[I]
=m
(Meter)
Die mittlere freie Weglänge wird für die Berechnung von Transporterscheinungen in Gasen benötigt, insbesondere für die Diffusion, die innere Reibung und die Wärmeleitung
in Ga en. Bei Kenntnis des Wirkungsradius d läßt sich die mittlere freie Weglänge leicht
berechnen. Als Bei piele führen wir folgende Werte an:
Stoff
Wirkung radius in 10-
10
m
2,98
3,18
2,47
Bei Normbedingungen wird die Teilchendichte N / V durch die LOSCHMIDT-Kon tante
gegeben. Um nun unter anderen, davon abweichenden Bedingungen N / V nicht gesondert
berechnen zu müs en, kann Gleichung (20.19) herangezogen werden, wobei sich dann
l
kT
= --=-2
(20.30)
Mittlere freie Weglänge
n.J2d p
ergibt.
Beispiele:
1. Für Wa ser toff ist nach (20.29) die mittlere freie Weglänge bei 0
1
,=-~-n.../2d 2 NL
oe und
1020 m 3
- - = - - - - - - - - - = ],38 . 10-7
n.J2 . 2, 472 m2 . 2,69 . 1025
l 013,25 hPa
m
Demnach erleidet ein Wa serstoffmolekül auf einer Strecke von 1 cm fast 100000 Zusammen töße,
womit die Bahn zu einer vöHig unregelmäßigen Zickzacklinie wird.
2. Berechne die mittlere freie Weglänge in Wasserstoff bei 20
(= 10- 9 Pn mÜ Nonndruck Pn; sogenanntes Hochvakuum).
oe und einem Druck von
101,3 jLPa
Nach (20.30) i t
1=
kT
n·JicJ2p
1,38.10- 23 Nm · 293, 2 Km 2
---=------------K · n.J2 .2,472 . 10- 20 m2 . 101,3 . 10- 6 N
=
]47 m
21 Kreisprozesse und zweiter Hauptsatz der Wärmelehre
Die bisher be prochenen Zu tandsänderungen der Gase sind von grundlegender Bedeutung
für die Wirkungsweise aller Wärmekraftma chinen. In einem sich periodi ch wiederholenden Arbeit zyklu wird dabei der Ma chi ne Wärme (z. B. unter Verwendung von Dampf,
21.1
Wirkung wei e einer Wärmekraftma chine
303
gasförmigen oder ftü igen Brennstoffen) zugeführt und in mechanische Arbeit umgewandelt. Der Druck p, da Volumen V und die Temperatur T müssen also nach jedem Arbeitszyklu wieder ihre ur prüngLichen Werte annehmen . Wenn das nicht der Fall wäre,
würde mindesten eine dieser Zu tandsgrößen im Laufe der Zeit immer im gleichen Sinne
anwachsen oder abnehmen, was aber einen technisch durchführbaren Dauerbetrieb unmöglich machen würde. Daher heißt der sich dabei vollziehende Vorgang Kreisprozeß.
Würde z. B. bei einem Viertakt-Benzinmotor von n = 3000 l/min die Temperatur am
Ende eines Zyklu nur um 1 K höher gegenüber vorher sein, so wäre sie bereits nach 1 min
um 1 500 K ge tiegen.
Demnach arbeiten alle Wärmekraftmaschinen, gleichgültig, ob es sich um eine Kolbendampfmaschine, eine Dampfturbine, einen Benzin-, Gas- oder Dieselmotor handelt, nach
gemeinsamen physikalischen PIinzipien. Um vorer t das Wesen der sich dabei abspielenden Krei prozes e deutlicher zu machen, ei die an Hand des bekannten, in vielen Kraftfahrzeugen eingebauten Viertakt-OTTO-Motors näher betrachtet.
Im Abschnitt 18.2 war die Vereinbarung genannt,jede dem System zugeführte Energie oder
Arbeit positiv und jede vom System abgegebene Energie oder Arbeit negativ zu zählen.
Diese Vereinbarung wird beibehalten, auch wenn es nicht sehr sinnvoll erscheint, die Arbeit
einer Wärmekraftmaschine negativ zu rechnen .
Arbeitsberechnung bei Kreisprozessen
21.1
(21.1)
Wirkungsweise einer Wärmekraftmaschine
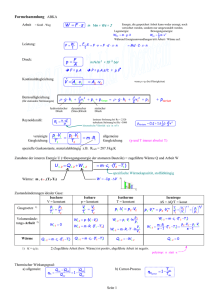
Die einzelnen Arbeitstakte des Viertakt-OTTO-Motors werden zweckmäßig in einem p, VDiagramm dargestellt. Das ent tehende Arbeitsdiagramm ist in der folgenden Darstellung
jedoch chematisch vereinfacht. In Wirklichkeit gehen die einzelnen Linien stetig ineinander über.
1. Takt: Ansaugen. Bei offenem Einlaßventil saugt der nach unten gehende Kolben ein
Benzin-Luft-Gemisch an (Bild 21.1). Dieses wird im Vergaser herge teIlt, wo der an einer
Düse vorbei streichende Luftstrom da Benzin zerstäubt. Im Arbeitsdiagramm entsteht die
parallel zur V -Achse verlaufende Linie 1 (Bild 21.2). Es ist dies eine Isobare.
2. Takt: Verdichten. Bei geschlossenen Ventilen bewegt sich der Kolben nach oben und
drückt den Zylinderinhalt im Verhältnis von etwa 8 : 1 zu ammen. Wegen der Schnelligkeit
dieses Vorganges ist die im Diagramm er ichtliche Arbeitslinie 2 eine Adiabate.
3. Takt: Explosion und Entspannung. Kurz vor der höchsten Kolben teIlung wird da
Brenn toffgemi ch durch einen an der Zündkerze über pringenden elektri chen Funken gezündet. Es verpufft ehr schnell, so daß Druck und Temperatur augenblicklich ansteigen.
Es entsteht die Arbeitslinie 3a (eine Isochore). Anschließend chiebt der Druck den Kolben
vorwärts, wodurch sich die Adiabate 3b ergibt.
4. Takt: Auspuff. Da Au laßventil öffnet ich, der Druck fällt sofort ab und ergibt die
Isochore 4a. Der wieder zurückgehende Kolben schiebt die Verbrennungsga e hinau (Linie 4b).
21
304
Krei proze e und zweiter Haupt atz der Wärme1ehre
~
~z'"
A
E
E
...
'
;:. :.
.
A
E
~.",
~".
o
o
o
a)
b)
c)
d)
Bild 21.1: Arbeit wei e des Viertakt-OTTo-Motor : a) An augen, b) Verdichten, c) Explo ion und
Entspannung (Arbeit takt), d) Au puff
v----
Bild 21.2: Arbeit diagramm de
Viertakt-OTTo-Motor (idealisiert)
Beim näch ten Arbeit zyklu liegen wieder genau die gleichen Verhältni e vor. Da Arbeitsdiagramm wird in immer gleicher Wei e durchlaufen der Kurvenzug gibt mithin einen
Krei 'prozeß wieder.
Er kann nun gedanklich in zwei Teile zerlegt werden, wie die auf Bild 21.3 gezeigt i t. Der
er te Teil a) teIlt denjenigen Teil de Krei proze es dar, im Verlaufe de en das Volumen
V zunimmt. Die unter die er Kurve liegende Fläche kennzeichnet dann die Arbeit WI, die
da Ga abgibt wenn e ich au dehnt. Sie kann al Integral (21.1)
au gedrückt werden, und die e nimmt einen negativen Wert an. Wie zu ehen ist chließt
der zweite Teil b) de Kurvenzuge mit der Ab zi e einen viel kleineren Aächenbetrag
21.1
Wirkung wei e einer Wärmekraftma chine
v,
dV
v---:"~
305
Vz
V---i"~
a)
b)
Bild 21.3: Die im Arbei diagramm (Bild 21.2) enthaltenen Arbeit beiträge: a) abgegebene Arbeit,
b aufzuwendende Arbeit; punktiert: gewonnene Arbeit
ein. Die zugehörige Arbeit W2 kann ebenfali a1 Integral
aufgefaßt werden. Die es hat einen po itiven Wert und reprä entiert die zur Verdichtung
aufzuwendende Arbeit. Die von der Ma chine gelieferte Arbeit i t omit im ganzen
Ihr ent pricht im p V -Diagramm die Differenz der beiden ent prechenden Flächenbeträge
und mithin die vom ge amten Kurvenzug um chlo ene Fläche:
Der von der rbeitskurve eines Kreisprozesses umschlossene Flächeninhalt
stellt die während eines rbeitszykJus gewonnene Arbeit dar.
Auch die bei den anderen Wärmekraftma chinen ablaufenden Krei proze e la . en ich
durch ent prechende Arbeit diagramme veran chaulichen. Je nach ihrer Arbeit wei e haben die von den einzelnen Kurven um chlo enen Flächen unter chiedliche Form. Man
kann ie jedoch tet in der be chriebenen Wei e al Differenz zweier Einzelftächenbeträge
betrachten.
Das Ergebni i t aber in jedem Fall, daß die letzten Endes gewonnene Arbeit W aL Differenz zweier Wärmemengenbeträge er cheint:
1Q 11 -
1Q21
= Q1
+ Q2 =
- W > 0
Die Wärmemenge QI i t d r Ma chine zuzuführen, während die Wärmemenge Q2 von
der Ma chine wieder abgegeben wird. Für die Beträge gilt 1 Q 11 > 1Q2 1. Dabei i tauch
21
306
Kreisprozesse und zweiter Haupt atz der Wärmelehre
17
Wiirmebehiilfer
hoher Temp.
\ 'W<O
-r~~---'7-----~I~Nu-t~M-r~be~i~tl
Wä rmebehölter
niederer Temp
Tl
Bild 21.4: Energieflußdiagramm
einer Wärmekraftmaschine
immer die Temperatur Tl, bei der sich die Wärme Q 1 in Arbeit verwandelt, höher als die
Temperatur T2, mit der das entsprechende Arbeitsmedium (Verbrennungsgase, Abdampf)
die Ma chine wieder verläßt (Bild 21.4).
Al Wirkungsgrad '1 einer Wärmekraftmaschine wird daher das Verhältnis der in Arbeit
W umgewandelten Wärmemenge Q 1 + Q2 zur gesamten zugeführten Wärmemenge Q I
definiert. E ist also
Thermischer Wirkungsgrad
(21.2)
Wegen Q2 < 0 und Q 1 > 0 ist natürlich '1 < 1.
Die Aufgabe der Technik besteht darin, diesen Wirkungsgrad möglichst günstig zu gestalten, also die Wärmeverluste I Q21 weitgehend zu vermindern.
Im Ab chnitt 21.4 wird gezeigt, daß es hier prinzipielle Grenzen gibt und es praktisch nicht
möglich ist, eine bestimmte Wärmemenge Q 1 vollständig in mechanische Arbeit umzuwandeln.
21.2 Kältemaschine und Wärmepumpe
Durchläuft man jedoch das Arbeitsdiagramm im entgegengesetzten Sinn, so müssen sich
alle Proze se umkehren. Dies wird technisch in der Kältemaschine und bei der Wärmepumpe verwirklicht. In diesen Anlagen laufen Kreisprozesse ab, die sich nach dem Schema
von Bild 21.5 vollziehen. Beim oberen Kurvenverlauf in a) wird ein zweckmäßig gewählter
Arbeits toff, z. B. Ammoniakgas, unter Aufwand von mechanischer Arbeit zusammengepreßt, wobei das unter die em Kurventeilliegende Flächenstück und damit die Arbeit Wl
bzw. da Integral
21.2
Kältema chine und Wärmepumpe
307
pOSitIve Vorzeichen erhält. Beim unteren Kurvendurchlauf b) entspannt sich der Arbeitstoff wieder, womit die nunmehr betragsmäßig kleinere Fläche einer Arbeit W2 mit negativem Vorzeichen entspricht. Die Differenzfläche ist damit gleich der insge amt aufzuwendenden Arbeit
v--.~
o}
b)
V---l·~
Bild 2l.5: Umgekehrt ablaufender Kreisprozeß: a) aufgewandte Arbeit, b) abgegebene Arbeit;
punktiert: in Wärme umgewandelte Arbeit
Ihr entspricht eine bestimmte Wärmemenge
die als Gegenwert diese Arbeitsaufwandes von der Maschine geliefert wird. Dabei wird
die Wärmemenge Q 1 bei der höheren Temperatur Tl nach außen hin abgegeben und die
Wärmemenge Q2 bei der niederen Temperatur T2 von außen her aufgenommen, wobei für
die Beträge IQ 11 > IQ21 gilt.
T7
Umgebung
I
I
I
\
'-w-.--
'.....
W>O
INutzenergie I
Kühlraum
12
Bild 21.6: Energieflußdiagramm einer Kältemaschine
Es wird praktisch kältere Wärme Q2 der Temperatur T2 durch Arbeitsaufwand W von außen auf höhere Temperatur gebracht (gepumpt) und dann a1 höherwertige Wärme Q1 an
21
308
Kreisprozesse und zweiter Haupt atz der Wärmelehre
das Wärmereservoir der Temperatur Tl abgegeben. Das gescrueht dadurch, daß die Wärmemenge Q2 einem entsprechenden Arbeitsmedium entzogen wird, welche sich dabei
abkühlt. Wenn die Anlage so eingerichtet ist, daß die hierbei entstehende Abkühlung genutzt wird, so erhält man eine Kältemaserune (Bild 21.6).
Eine Kompressionskältemaschine arbeitet folgendermaßen (Bild 21 .7): Mittels einer Pumpe wird Ammoniakdampf im Kompressor an gesaugt und verdichtet. Die Kompressionsund die Kondensationswärme Q I wird im Kondensator abgegeben. Das teilweise verflüssigte Ammoniak wird danach entspannt und nimmt im Verdampfer die Wärme Q2 aus dem
Kühlraum auf.
Kompressor
-20·C
Verdampfer
Q, ~
Abgabe der
Kondensationswärme
Kühlraum
+20·C
Drosselventil
Bild 21.7: Schema der
Ammoniak- Kältemaschine
Derselbe Grundvorgang ist aber noch in anderer technischer Form verwirklicht, und zwar
so, daß e auf die Verwertung der bei der höheren Temperatur TI entstehenden Wärmemenge Q 1 ankommt. Dies geschieht in der Wärmepumpe. Die Verdampfung und Entspannung geht an einem Ort vor sich, wo die entstehende Kälte nicht weiter stört, z. B .
in einem nahe gelegenen Fluß oder See, auch in der Außenluft, im Erdreich oder Grundwa sero Eine Pumpe komprimiert das Gas in einem Wärmespeicher, wo es seine Wärme
Q J an Was er abgibt, das, in Heizkörpern zirkulierend, zur Heizung von Räumlichkeiten
dient. Die den Heizkörpern entströmende Wärme ist also zweierlei Ursprungs: einerseits
Kondensationswärme des Ammoniaks, die als Verdampfungswärme Q2 dem Verdampfer
entnommen wird, andererseits die von der Pumpe durch den Aufwand mechanischer Arbeit
Werzeugte Verdichtungswärme (Bild 21.8).
Wärmepumpen arbeiten bei gegebenen Voraussetzungen außerordentlich wirtschaftlich.
Sie liefern an nutzbarer Wärme das Zwei- bis Vierfache des zum Betrieb der Pumpe erforderlichen elektri chen Energieaufwandes.
21.3
Reversible und irreversible Vorgänge
Das Streben nach einem möglichst großen Wirkungsgrad." hängt nun aufs engste mit der
Frage zusammen, inwieweit sich Vorgänge der Energieumwandlung, in besondere die der
gegenseitigen Umwandlung von mechanischer Arbeit und Wärme, umkehren lassen oder
nicht. E geht darum, ob z. B. durch Wärmeabgabe an die Umgebung oder durch ungenutzten Temperaturau gleich oder nichtnutzbare Strömungen im Arbeitsga oder anderweitig
Verlu te ent tehen, die eine prinzipielle Umkehrung der Energieumwandlung unmöglich
machen oder einen zusätzlichen Arbeit aufwand von außen erfordern würden.
21.3
Reversible und irrever ible Vorgänge
309
T1
Heizkörper
INu tzenergie I
II
\ '-..............-_ __
W>O
Umgebung
Tz
Bild 21.8: Energieflußdiagramm einer Wärmepumpe
Denken wir an einen völlig wärmedicht umhüllten Zylinder, in dem sich ein Kolben ohne jede Reibung auf und ab bewegen kann, so wird der Gasinhalt beim Hineingehen des
Kolbens adiabatisch verdichtet. Die gesamte aufgewandte mechanische Arbeit erscheint
in Form von Wärme und bleibt als zusätzliche innere Energie im Gas gespeichert. Beim
Loslassen des Kolbens wird dieser wieder nach außen getrieben. Die zuvor gebildete Wärme verwandelt sich restlos wieder in mechanische Arbeit zurück. Man nennt dies einen
vollständig umkehrbaren oder reversiblen Vorgang (B ild 21.9):
entstandene
Wärme
~
verbrauchte
Wärme
N
Bild 21.9: a) Rever ibler Vorgang: adiabatische Verdichtung und Entspannung,
b) lrreversibler Vorgang: Reibung zweier Holzklötze
Ein Vorgang ist reversibel, wenn nach seinem Ablauf der Anfangszustand vollständig wiederherstellbar ist, ohne daß Veränderungen zurückbleiben.
Ein reversibler Vorgang ist ein solcher, der ebensogut auch in umgekehrter Richtung durchgeführt werden oder ablaufen kann. Es gibt auch keine Veränderungen der Umgebung.
Da bei einem reversiblen Vorgang keinerlei Wärmeverluste auftreten, wird bei einem reversibel gefÜhrten Kreisprozeß einer Wärmekraftmaschine die maximal mögliche Arbeit
abgegeben.
310
21
Kreisprozesse und zweiter Haupt atz der Wärmelehre
Reibt man dagegen zwei Holzstücke gegeneinander, so wandelt sich ebenfalls mechanische
Arbeit in Wärmeenergie um (Bild 21.9b). Diese Wärme wird sich aber beim Aufbören
des Reibungsvorganges auf keinen Fall wieder in mechanische Arbeit zurückverwandeln.
Infolge von Wärmeleitung wird sie sich sofort zwischen den bei den Körpern verteilen, und
es ist keine Vorrichtung denkbar, die eine vollständige Rückverwandlung in mechani che
Arbeit ermöglichen könnte. Solche Vorgänge heißen nicht umkehrbar oder irreversibel.
Ein Vorgang ist irreversibel, wenn er nur durch Veränderung der Umgebung,
z. B. durch Arbeit von außen, rückgängig gemacht werden kann.
IlTever ible Vorgänge verlaufen von selbst nur in einer Richtung, und es wird dabei Arbeit
vergeudet, wie die Reibungsverluste bei obigen Beispielen. Ein weiterer typischer irreversibler Vorgang ist die adiabati che Ausdehnung eines Gases, wenn die Trennwand zwischen
gefülltem und leerem Behälter entfernt wird. Auch die Durchmischung zweier Gase nach
Entfernen einer Trennwand ist irreversibeL
Ein prinzipiell wichtiger irreversibler Vorgang ist die Wärmeleitung. Temperaturunterschiede zwi chen heißen und kalten Körpern gleichen sich von selbst aus. Eine Umkehrung ist
zwar mit einer Kältemaschine prinzipiell möglich, erfordert aber Arbeit aus der Umgebung.
Schwieriger ist es, wirklich reversible Vorgänge zu finden. Wird von Reibung abgesehen
o können wir viele Vorgänge in der Mechanik, z. B. das Schwingen eines Pendels oder die
Reflexion einer Stahlkugel auf einer Spiegelglasplatte, als reversibel betrachten. Genaugenommen aber gibt es streng reversible Vorgänge in der Natur überhaupt nicht. Sie stellen
nur ideale Grenzfälle dar.
So ist auch die i otherme Verdichtung eines Gases grundsätzlich irreversibel, weil die nach
außen abfließende Wärme niemals von selbst wieder in den Zylinder zurückfließen wird.
Wird angenommen, der Zylinder steht mit einem unendlich großen Wärmebehälter in Verbindung, dessen Temperatur sich von der des Zylinders nur um einen unendlich kleinen
Betrag unter cheidet, so stünde einer Rückkehr der Wärme und ihrer Rückverwandlung
in Arbeit nichts im Wege (s. quasistatischer Prozeß in 19.3). Unter dieser allerdings sehr
gekünstelten und techni ch niemals realisierbaren Voraussetzung könnten auch isotherme
Proze e reversibel ablaufen.
Halten wir also fest, daß adiabatische und i otherme Prozesse im idealen Fall reversibel gefülut werden können. Eine Wärmekraftmaschine, die mit solchen Prozessen arbeitet, wird
unter gegebenen Bedingungen den höchsten Wirkungsgrad erreichen. Da gilt insbesondere für die CARNOT-Maschine.
21.4
Carnotscher Kreisprozeß
Wie wjr oeben ge ehen haben, können einsinnig verlaufende adiabatische oder isotherme
Prozes e in gewissen Grenzfallen rever ibel, d. h. mit maximalem Wirkungsgrad vor sich
gehen. Dann muß ein Krei prozeß, der sich au einzelnen reversibel ablaufenden Teilproze en zu ammen etzt, ebenfall den denkbar günstigsten Wirkungsgrad aufweisen. Einen
olchen Krei prozeß erdachte der Franzose SADI CARNOT (1796-1832). Bemerkenswert
i t dabei , daß CARNOT eine Theorie bereits zu einer Zeit darstellte, als die Entwicklung
der Dampfma chine noch in den ersten Anfängen stand.
21.4
CARNOTscher Kreisprozeß
311
Den CARNOT chen Krei prozeß können wir uns ähnlich einem ohne alle mechanische
Energieverluste arbeitenden Heißluftmotor vorstellen, dem die Gesetze des idealen Gases zugrunde liegen (Bild 21.10). Ein Arbeitszyklus verläuft in 4 Takten, die wir im p, VDiagramm verfolgen wollen (Bild 21.11):
t
t
...
... T
Q2
...
...............
... ........... ...
::::::::::::::::::::::::::::
:::~~
::::::::::: :::::::::::::
a)
b)
c)
d)
Bild 21.10: Verlauf
des CARNoTsehen
Kreisprozesses:
a) 1. Takt, b) 2. Takt,
e) 3. Takt, d) 4. Takt
1. Takt: Bei der tiefsten Kolbenstellung wird der eingeschlos enen Luft eine bestimmte
Wärmemenge Ql bei gleichbleibender Temperatur Tl reversibel, d. h. unter Vermittlung
eines unendlich großen Wärmebehälters von der Temperatur Tl zugeführt. Die Luft dehnt
sich aus und verrichtet Arbeit. Die verbrauchte Wärme ist nach (19.7)
V2
Q1 = m R sTl In -
VI
> 0
Dies gibt die Isotherme 1.
2. Takt: Der Zylinder wird wärmedicht umhüllt. Das Gas dehnt ich weiter aus und kühlt
sich auf T2 ab. Es entsteht die Adiabate 2.
t
p
Bild 21.11: p. V -Diagramm de
CARNOTsehen Kreisproze 'se
3. Takt: Die im Schwungrad gespeicherte Energie treibt den Kolben zurück. Die Umhüllung de Zylinders lassen wir dabei fallen, 0 daß die freiwerdende Verdichtung wärme
21
312
Kreisprozesse und zweiter Haupt atz der Wärmelehre
in einen ebenfalls unendlich großen Wärmebehälter von der Temperatur T2 bei konstanter
Temperatur T2 abfließen kann. Isotherme 3. Die abfließende Wärme ist
V4
V3
= -mRsT2ln - < 0
V3
V4
Q2 = mR sT2 ln -
4. Takt: Schließlich wird nach abermaliger Umhüllung des Zylinders der Gasinhalt auf das
Anfangsvolumen VI verdichtet, wobei die Temperatur wieder auf den anfänglichen Wert
Tl ansteigt: Adiabate 4.
Nach Beendigung dieses Zyklus ist der Ausgangszustand wiederhergestellt.. Das Ergebnis
ist folgendes. Takt 2 liefert genausoviel Arbeit, wie Takt 4 verzehrt~ denn diese hängt bei
adiabatischen Vorgängen nach (19.14) lediglich von den Temperaturen Tl und T2 ab, die
hier übereinstimmen. Ferner gilt für diese beiden Takte nach (19.10):
T
T2
_1
= (V)K-I
-.2
= (Y.
~
V2
VI
)K-I ,
woraus sich ergibt:
Dividiert man den Ausdruck für Q2 durch den für Ql, so ergibt sich wegen der eben festgestellten Gleichheit der Volumenverhältnisse die Beziehung
Q2
T2
Ql
Tl
----
(21.3)
Damit wird auf Grund von (21.2)
1~=TI;T2=1-tl
Thermischer Wirkungsgrad
des Carnot-Prozesses
(21.4)
Dieser ist demnach nur von den bei den Temperaturen abhängig, bei denen der Wärmeau tausch stattfindet. Von allen denkbaren Kreisprozessen, die zwischen den Temperaturen
TI und T2 arbeiten, hat der CARNOT-Prozeß den günstigsten Wirkungsgrad. Das geht bereits daraus hervor, daß er in allen seinen Teilen reversibel verläuft. Folglich ist auch der
CARNOT-Prozeß im ganzen umkehrbar.
Der Carnot-Prozeß ist vollständig umkehrbar (reversibel).
Läßt man ihn in entgegengesetzter Richtung ablaufen, so wird er als ideale Kältemaschine
funktionieren. Nach je einem Vorwärts- und einem Rückwärtsgang ist auch in der Umgebung der Au gang zustand vollständig wiederhergestellt.
Damit hat auch der in Gleichung (21.4) stehende Bruch (Tl - T2) / Tl den größtmöglichen
Wert. Bei allen technischen Motoren vollzieht ich die Umwandlung der Wärme QI in mechani che Energie unterhalb der höchsten Arbeitstemperatur Tl. Ebenso setzt die Ableitung
der Wärmemenge Q2 bereits vor dem Erreichen der tiefsten Temperatur T2 ein, so daß der
Quotient Q2/ Q L stets dem Betrage nach einen größeren Wert hat, als ihn Gleichung (21.3)
angibt. Damit i t auch der nach Gleichung (21.2) definierte Wirkungsgrad in jedem Fall
kleiner al der des CARNOT-Prozesses. Aus (21.4) ist ferner zu ersehen: Ein Wirkungsgrad
von 1, d. h. 100 %, kann selb t bei diesem idealen Fall niemals erreicht werden, da der
Zähler de Bruches tets kleiner als der Nenner ist.
21
314
Krei proze e und zweiter Hauptsatz der Wärmelehre
Der Wirkung grad ist im Idealfall nach (21.2) 17 = QI
+ Q2
QI
und anderer eit nach (21.4)
17 = Tl - T2. Nach Gleich etzen folgt für die bereitzustellende Wärmeenergie
Tl
Ql
= (Ql + Q2)TI = W
+ Q2
Tl - T2
Tl
Tl - T2
= - W den Energieaufwand (Elektroenergie) W = 100 kJ dar teilt. Damit wird
-100 kJ . 323 K
Q1 =
50 K
= -646 kJ
die bei der höheren Temperatur 1Jl = 50 oe zur Verfügung teben. Da Verhältnis von Nutzenergie
(Bild 21.8) zu Aufwandsenergie ergibt sich hier zu QI/ W = 6,46 (Leistung zahl). In der Praxi
werden Leistungszahlen von etwa 3 bis 4 erreicht.
wobei QI
21.5
21.5.1
Zweiter Hauptsatz der Wärmelehre
Entropie beim Carnotschen Kreisprozeß
Ob nun ein Vorgang rever ibel oder irreversibel verläuft, läßt sich mit Hilfe des 1. Hauptatzes, der nur eine spezielle Fassung des Ge etzes von der Erhaltung der Energie ist, nicht
ent cheiden. Bei beiden Arten von Vorgängen bleibt die Gesamtsumme der Energie konstant. Es fragt sich also, ob es eine physikalische Größe gibt, die al Gradme ser für die
Irreversibilität irgendweIcher Naturvorgänge verwendet werden kann. Man findet sie an
Hand de CARNOT-Proze ses der von vornherein so angelegt ist, daß er reversibel verläuft.
Hierbei stoßen wir auf die Beziehung (21.3) Q 1
Q2
= _ Tl .
T2
Durch Umformung ergibt sich hieraus Q I - _ Q2 oder
Tl
T2
(21.5)
Q 1 und Q2 bedeuten die beiden auf reversiblem Weg bei den Temperaturen Tl und T2 ausgetau chten Wärmemengen, was durch die Schreibweise Qrev I und Qrev 2 noch besonders
betont werden oll.
Dieser beim CARNOT -Prozeß (und anderen reversibel gedachten Vorgängen) auftretende
Quotient Qrev/T wurde von CLAUSIUS (1854) als Entropieänderung I1S bezeichnet.
Er führte den Beweis, daß die Entropie S ähnlich der Energie eine charakteristische Zutandsgröße ist von der man jeweils agen kann, ob sie während eines Vorganges zu- oder
abnimmt oder auch unverändert bleibt.
reversibel ausgetauschte Wärmemenge
Entropieänderung = - - - - - - = - - - - - - - - - Austauschtemperatur
I ßS
Q;ev I
Entropieänderung
[I1S] = J /K (Joule je Kelvin)
(21.6)