Inhalt - Institut für Elektrische Energiewandlung
Werbung

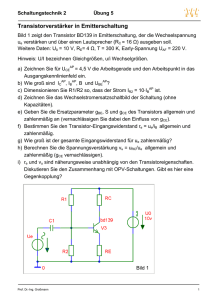
Universität Stuttgart Institut für Leistungselektronik und Elektrische Antriebe Abt. Elektrische Energiewandlung Prof. Dr.-Ing. N. Parspour Inhalt 4 Halbleiterelektronik – Bipolartransistor ...................................................................... 4-18 4.3 Der Bipolartransistor ............................................................................................ 4-18 4.3.1 Aufbau und Funktionsweise von Bipolartransistoren ...................................... 4-18 4.3.2 Das Kennlinienfeld .......................................................................................... 4-20 4.3.3 Transistorersatzschaltbilder ............................................................................. 4-25 4.3.4 Grundschaltungen des Bipolartransistors ........................................................ 4-29 4.3.5 Die Emitterschaltung ....................................................................................... 4-30 4.4 Wechselstrom-Transistorverstärker ..................................................................... 4-32 4.4.1 Funktionsprinzip der Emitterschaltung als Verstärker .................................... 4-32 4.4.2 Wechselstromverstärker in Emitterschaltung .................................................. 4-35 4.4.3 Arbeitsgerade und Aussteuerbarkeit von Verstärkern ..................................... 4-43 4.4.4 Ersatzschaltbild des Wechselstromverstärkers ................................................ 4-44 4-18 4 Halbleiterelektronik – Bipolartransistor 4.3 Der Bipolartransistor Der Transistor wurde 1947 vom Forscherteam Shockley, Bardeen und Brattain erfunden (zunächst als Spitzentransistor, ein Jahr später dann als Flächentransistor). Er war das erste verstärkende Bauelement auf Halbleiterbasis und verdrängte innerhalb von 20 Jahren die Elektronenröhre weitgehend aus der Signalelektronik. Der erste Transistor war ein sogenannter Bipolartransistor, d.h. im Bauelement findet sowohl Elektronen- als auch Löcherleitung statt. Später wurden auch Unipolar-Transistoren realisiert (z. B. Feldeffekttransistoren). 4.3.1 Aufbau und Funktionsweise von Bipolartransistoren Der Bipolartransistor ist eine Weiterentwicklung der Halbleiterdiode. Er ist aus drei unterschiedlich dotierten Halbleiterschichten aufgebaut. Man unterscheidet NPN- und PNPTransistoren. Bild 4.17 Aufbau (Halbleiterschichten) des Bipolartransistors Die Elektroden werden Emitter (E), Basis (B) und Kollektor (C) genannt. Man kann sich einen Transistor als Reihenschaltung zweier Dioden vorstellen, von denen die Basis-EmitterDiode in Durchlassrichtung und die Basis-Kollektor-Diode in Sperrrichtung betrieben wird, d. h. beim NPN-Transistor gilt UBE > 0 und UCE > 0 bzw. beim PNP-Transistor UBE < 0 und UCE < 0 (siehe Bild 4.18). Wenn im Basis-Emitterkreis eines NPN-Bipolartransistors ein in technischer Richtung positiver Strom IB fließt, fließen auch Elektronen vom Emitter in die Basis. Diese rekombinieren mit den Löchern in der Basis. Da dieser Vorgang eine gewisse Zeit benötigt, Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-19 fließen einige Ladungsträger sehr weit in die Basis hinein. Bei einer geringen Dicke der Basis werden sie vom äußeren Feld durch UCE am Kollektor „angezogen“ und können bis zum Kollektor gelangen. Hier werden diese Ladungsträger abgesaugt und gelangen nicht mehr zur Basis-Elektrode. Dieser Vorgang führt zu einem Strom in den Kollektor. Bild 4.18 Funktionsweise eines NPN-Transistors Bei einer systematischen Untersuchung kann man feststellen, dass der Kollektorstrom IC mit steigendem Basisstrom IB ebenfalls ansteigt. der Kollektorstrom i. A. größer ist als der Basisstrom. Dieser Effekt wird Stromverstärkung genannt und ist der wesentliche Grund für den verbreiteten Einsatz von Transistoren. Aufgrund der hohen Bedeutung in der Elektronik hat der Transistor ein eigenes Schaltsymbol (Bild 4.19) bekommen. Die beiden Transistortypen werden durch die Richtung des (Dioden-) Pfeils an der Emitter-Elektrode unterschieden. Die Spannungspolaritäten sind beim PNPTypen umgekehrt wie beim NPN-Typen. Bild 4.19 Schaltsymbole von Bipolartransistoren Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-20 4.3.2 Das Kennlinienfeld Die Stromverstärkung ist ebenso wie die Strom-Spannungs-Kennlinie der Basis-EmitterDiode nichtlinear. Daher werden Transistoren meist durch Kennlinienfelder beschrieben. Die Kennlinienfelder werden mit Hilfe zweier variabler realer Spannungsquellen mit einstellbarer Spannung gemessen. Die häufigste Schaltung verwendet den Emitter als gemeinsames Bezugspotential für die beiden Quellen (sog. Emitterschaltung, Bild 4.20). Bild 4.20 Messschaltung zur Ermittlung des Kennlinienfeldes (Transistor in Emitterschaltung) In der gezeigten Emitterschaltung sind vier Größen am Transistor messbar: UCE, UBE, IC und IB. In einer vollständigen Darstellung der Kennlinien werden die vier Größen an den vier Achsen eines orthogonalen Koordinatensystems aufgetragen. Im folgenden Bild 4.21 ist das Kennlinienfeld eines Silizium-NPN-Transistors gezeigt. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-21 Bild 4.21 Kennlinienfeld des NPN-Transistors vom Typ BC 108 Im ersten Quadranten wird die Ausgangskennlinie IC = f(UCE) bei verschiedenen Werten für IB aufgetragen. Die Kollektor-Emitterspannung UCE hat oberhalb eines Schwellwerts UCE > 0,4 .. 0,5 V nur einen geringen Einfluss auf den Kollektorstrom IC. In Verstärkerschaltungen können der Knick in der Kennlinie und die Steigung meist vernachlässigt werden: IC ≠ f(UCE). Das Produkt UCE . IC bestimmt den größten Teil der Verluste und damit die abzuführende Wärme im Transistor. Daher ist der im Ausgangskennlinienfeld gewählte Arbeitspunkt (hier beispielhaft eingezeichnet: Kollektor-Emitter-Spannung im Arbeitspunkt UCEA = 5 V, Kollektor-Emitter-Strom im Arbeitspunkt ICA = 42 mA) vor allem für die Verlustberechnung von Bedeutung. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-22 Im zweiten Quadranten wird die Stromverstärkungskennlinie IC = f(IB) aufgezeichnet. Diese ist nahezu unabhängig von der Spannung UCE. Der Strom IC ist viel größer als IB, es gilt: IC = B . IB (4.11) Die Größe B wird als Gleichstromverstärkung bezeichnet und ist in der Größenordnung von: B ≈ 5-5001. Aus dem Diagramm ist zu erkennen, dass sich bei hohen Strömen die Gleichstromverstärkung verringert. Leistungstransistoren, die hohe Ströme leiten müssen, haben kleine Verstärkungsfaktoren. Kleinsignaltransistoren, die für kleine Ströme aber hohe Frequenzen, ausgelegt sind, haben relativ hohe Stromverstärkungen. Für kleine Abweichungen vom Arbeitspunkt kann die Kurve IC = f(IB) durch eine Gerade angenähert werden. Dieser Vorgang entspricht der Linearisierung der Ausgangskennlinie in einem kleinen Bereich um einen Arbeitspunkt (Bild 4.22). Dazu wird die Wechselstromverstärkung β wie folgt definiert: β = ∆ΙC/∆ΙB (4.12) Die Wechselstromverstärkung liegt üblicherweise im Bereich von β ≈ 5 .. 500. Für den gewählten Arbeitspunkt im Diagramm 4.22 mit IBA= 0,15 mA kann berechnet werden: B = ICA/IBA = 42 mA/0,15 mA = 280 β = ∆ΙC/∆ΙB = (55 - 28) mA / (0,22 - 0,1) mA = 225 1 In der Literatur wird B auch als hFe oder h21 bezeichnet. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-23 Bei einer geringen Variation des Basisstrom von ± ∆I B um einen Arbeitspunkt IBA wird 2 zur vollständigen Beschreibung zusätzlich die Wechselstromverstärkung β benötigt: ICA ± ∆IC ∆I = B ⋅ I BA ± β ⋅ B 2 2 (4.13) Bild 4.22 Kennlinienfeld des NPN-Transistors vom Typ BC 108 mit dem beispielhaft eingezeichneten Arbeitspunkt UCE = 5 V und IC = 42 mA Eine solche geringe Variation kommt beispielsweise bei Wechselstrom-Verstärkern vor. Bei diesen Verstärkern wird nachdem ein Arbeitspunkt mit Gleichstromwerten UCEA, ICA, IBA, UBEA eingestellt ist, ein Wechselspannungssignal den Gleichstromwerten des Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-24 Arbeitspunkts überlagert. Zum Beispiel im Falle bei Überlagerung eines sinusförmigen Signals ergeben sich die Folgenden Zusammenhänge: i B = I BA + i B ⋅ sin(ω⋅ t + ϕiB ) mit ^ i B << I BA (4.14) daraus folgt: i C = ICA + β ⋅ i B ⋅ sin(ω⋅ t + ϕiB ) mit i C = I + β ⋅ i B CA (4.15) In den vorausgehenden Gleichungen sind iB und iC Mischgrößen, bestehend aus Gleichund Wechselanteil. Im dritten Quadranten wird die Eingangskennlinie aufgetragen. Sie entspricht von der Form her einer Diodenkennlinie in Durchlassrichtung und kann wie diese durch eine reale Spannungsquelle mit der Leerlaufspannung UBE0 und einem Widerstand RBE linearisiert werden (siehe bitte Kapitel 4.2.4.2): R BE = ∆U BE ∆I B (4.16) UBE0 repräsentiert die Diffusionsspannung des Emitter-Basis-Übergangs. In der Praxis beträgt der Wert von UBE0 ≈ 0,5 .. 0,6 V (etwas geringer als bei einer reinen Diode). Der Widerstand RBE beschreibt den Bahnwiderstand der Strecke Basis-Emitter und ist in der Größenordnung von einigen 10 Ω bis einigen 100 Ω. Für den im Diagramm 4.22 gewählten Arbeitspunkt im Eingangskennlinienfeld mit UBEA = 0,59 V gilt: R BE = ∆U BE ∆I B = (0,62 - 0,6) V / (0,22 - 0,1) mA = 167 Ω Der vierte Quadrant zeigt die Rückwirkungskennlinie, die den Einfluss der KollektorEmitterspannung UCE auf die Basis-Emitterspannung UBE wiedergibt. Da die Kennlinie parallel zur UCE-Achse verläuft, gilt praktisch UBE ≠ f(UCE). Die Rückwirkung kann daher in einer ersten Näherung vernachlässigt werden. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-25 4.3.3 Transistorersatzschaltbilder Aufgrund der Möglichkeit der Steuerung des relativ großen Kollektorstroms über die Veränderung des relativ kleinen Basisstroms bzw. der Basis-Emitter-Spannung liegt das Haupteinsatzgebiet des Bipolartransistors in Signalverstärkerschaltungen. Ein weiterer Anwendungsbereich des Bipolartransistors ergibt sich aus der Möglichkeit des Durchlassens des Kollektorstroms durch die Basis-Emitter-Spannung. Diese Charakteristik wird in elektronischen Schaltern benutzt. Abhängig von dem Einsatzgebiet des Transistors als Verstärker bzw. als Schalter ergeben sich die zugehörigen Ersatzschaltbilder: 4.3.3.1 Transistor-Ersatzschaltbild für Verstärkerschaltungen Bei den Verstärkern wird ein Wechselstromsignal mittels einer Transistorschaltung verstärkt. Dabei gelten die Zusammenhänge aus den Gleichungen (4.13) bis (4.16). Das Eingangssignal ist demnach ein Mischsignal, das aus einem Gleichstrom- und einem Wechselstromanteil besteht. Da das Verhalten des Bipolartransistors im Falle der Gleichstromgrößen von dem der Wechselstromgrößen unterscheidet, existiert für den jeweiligen Fall das entsprechende Ersatzschaltbild. Linearisiertes Gleichstromersatzschaltbild des Bipolartransistors Für einfache Berechnungen von Verstärkerschaltungen dürfen die Steigungen der Ausgangsund Rückwirkungskennlinien vernachlässigt werden. Die Ausgangskennlinien des Transistors im Arbeitsbereich der Verstärkerschaltungen verlaufen dann parallel zu der UCE-Achse. Das Verhalten kann dann mit einem einfachen Ersatzschaltbild beschrieben werden: Bild 4.23 Linearisiertes Gleichstrom-Ersatzschaltbild des Bipolartransistors Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-26 Der Eingangskreis wird durch den Basis-Emitterwiderstand RBE und die Konstantspannungsquelle UBE0 beschrieben. RBE und UBE0 werden nach der Linearisierung der Eingangskennlinie um einen Arbeitspunkt ermittelt. Der gestrichelt eingezeichnete Widerstand RCE beschreibt den Kollektor-Emitterwiderstand. Der Wert von diesem Widerstand ist im Arbeitsbereich des Transistors als Verstärker sehr groß und kann in den meisten Fällen vernachlässigt werden. Aus der Maschengleichung der linken Masche des Ersatzschaltbilds kann ermittelt werden: IB = U BE − U BE0 R BE (4.17) Ist die Basis-Emitter-Spannung UBE für einen Arbeitspunkt bekannt, so kann der Basisstrom IB für diesen Punkt mit Hilfe der obigen Gleichung und ohne Kenntnis der Eingangskennlinie berechnet werden. Dieses Ersatzschaltbild enthält ein neues Element: eine gesteuerte Stromquelle, dargestellt durch eine Raute. Bei einer gesteuerten Stromquelle ist der Quellstrom von einer weiteren Variablen (hier IB) abhängig: IC0 = B ⋅ I B (4.18) Diese Stromquelle im Ersatzschaltbild beschreibt den für den Transistor typischen Effekt der Stromverstärkung. Da der Kollektor-Emitterwiderstand einen sehr hohen Wert aufweist, ist in der Praxis IC0 ≈ IC, sodass die Gleichung (4.11) statt der Gleichung (4.18) verwendet werden kann. In einem beliebigen Arbeitspunkt gilt dann ICA0 = B ⋅ I BA , bzw. unter Vernachlässigung von RCE: I CA = B ⋅ I BA (4.19) Anmerkung 3: Die aufgetragenen Werte für UCE und UBE in den Achsen des Kennlinienfelds entsprechen den Werten der Spannungen, die an den (äußeren) Klemmen des Transistors gemessen werden können. Während UBE0 eine interne Spannung ist, die der Diffusions- Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-27 spannung des Emitter-Basis-Übergangs entspricht. UBE0 ist in einem kleinen Bereich um den Arbeitspunkt konstant. UBE (die Klemmenspannung) kann sich aber in diesem Bereich ändern. Anmerkung 4: Durch die Spannungsquelle UBE0 fließt ein Strom, der der Quellspannung gleichgerichtet ist. Daher wird in dieser Spannungsquelle Leistung verbraucht bzw. in Wärme umgesetzt. Linearisiertes Wechselstromersatzschaltbild des Bipolartransistors Bei der Entwicklung des Wechselstromersatzschaltbildes wird berücksichtigt, dass ein Wechselstromsignal den Gleichstromwerten des Arbeitspunktes linear überlagert ist. Unter der Annahme, dass die Amplituden des Wechselsignals viel kleiner sind als die Werte des Arbeitspunkts (Gleichung 4.14) können der Überlagerungssatz und das linearisierte Ersatzschaltbild (Bild 4.23) als Entwicklungsgrundlage für ein neues Ersatzschaltbilds für Wechselstromsignale benutz werden. Dazu wird im linearisierten Bild 4.23 die Gleichspannungsquelle UBE0 kurzgeschlossen. Zusätzlich werden die Sperrschichtkapazitäten zwischen dem Basis-Emitter-Übergang CBE und dem Basis-Kollektor-Übergang CBC berücksichtigt. Diese Kapazitäten sind im Ersatzschaltbild 4.24 gestrichelt gezeichnet. Die Basis-Emitter-Kapazität wird erst bei sehr hohen Frequenzen wirksam und kann gegenüber der Basis-Kollektor-Kapazität eher vernachlässigt werden. Die Kapazität CBC ist maßgebend für die obere Grenzfrequenz einer Verstärkerschaltung und kann im mittleren Arbeitsfrequenzbereichen vernachlässigt werden. Bild 4.24 Linearisiertes Wechselstrom-Ersatzschaltbild des Bipolartransistors Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-28 4.3.3.2 Transistor-Ersatzschaltbild für Schalteranwendungen Ein weiteres Anwendungsgebiet von Transistoren ist der Einsatz als elektronischer Schalter. Wird der Basisstrom bzw. die Basis-Emitter-Spannung sehr niedrig, verringert sich der Kollektorstrom auf einen Wert nahe Null. Die Kollektor-Emitter Strecke wird sehr hochohmig und der Schalter ist im „OFF“-Zustand. Umgekehrt, wenn die Basis-Emitter-Spannung ihren maximalen Wert hat, fließt ein hoher Kollektorstrom bei einer niedrigen KollektorEmitter-Spannung. Der Schalter ist dann im „ON“-Zustand. Bild 4.25 Arbeitspunkte des Transistors als elektronischer Schalter Der Transistor arbeitet im eingeschalteten Zustand im ersten Teil der Ausgangskennlinie im Bereich der niedrigeren Kollektor-Emitter-Spannungen. Die Kennlinie kann hier als eine Gerade mit einer steilen Steigung betrachtet werden. Bild 4.26 Linearisierung der Ausgangskennlinie des Bipolartransistors für Schalteranwendungen Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-29 Das elektrische Ersatzschaltbild passend zu diesem Teil der Kennlinie ist ein Ohmscher Widerstand mit RCEon (Widerstand im eingeschalteten „ON“-Zustand). Dieser Widerstand weist für sehr hohe Basisstromwerte einen niedrigen Wert auf und wirkt wie ein Schalter, der den Strom IC leitet. R CEon = ∆U CE / ∆IC (4.20) U CE ≈ R CEon ⋅ I C (4.21) 4.3.4 Grundschaltungen des Bipolartransistors Je nach Beschaltung der Elektroden werden drei Grundschaltungen des Bipolartransistors unterschieden. Sie werden nach der von Ein- und Ausgangsseite gemeinsam benutzten Elektrode benannt. Die Schaltungen weisen unterschiedliche Spannungs- (vU) und Stromverstärkungen (vI) auf. Allen gemeinsam ist eine Leistungsverstärkung v P = v U ⋅ v I , die bei sinnvoller Dimensionierung größer als eins ist. Bild 4.27 Transistor Grundschaltungen Die Emitterschaltung wird am häufigsten verwendet. Sie weist bei entsprechender Dimensionierung der Schaltung sowohl eine Strom- als auch eine Spannungsverstärkung größer eins auf. Die Phasenlage der Spannung wird um 180° gedreht. Die Basisschaltung hat eine Spannungsverstärkung, die viel größer als eins ist, und eine Stromverstärkung kleiner als eins. Sie hat vor allem in der Hochfrequenztechnik eine Be- Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-30 deutung, da sie die geringste parasitäre Gesamtkapazität für das Eingangssignal aufweist (CBC kann keinen Ausgangsstrom auf den Eingang zurückführen). Die Kollektorschaltung hat eine Spannungsverstärkung kleiner als eins und eine Stromverstärkung, die viel größer als eins ist. Sie wird vor allem zur Anpassung von hochohmigen Quellen an niederohmige Verbraucher eingesetzt (sog. Impedanzwandler). 4.3.5 Die Emitterschaltung Emitterschaltung ist die am meisten verbreitete Transistorschaltung. Zur Erklärung des Funktionsprinzips ist in Bild 4.28 die Grundschaltung dazu gezeichnet. Bild 4.28 Emitterschaltung mit einem NPN-Transistor Die hier dargestellte Emitterschaltung besteht aus einem Bipolartransistor, zwei Gleichspannungsquellen UBat1 und UBat2 und einem Widerstand RC. Die beiden Gleichspannungsquellen sind zusammen mit RC für die Einstellung des Arbeitspunkts zuständig. Dazu wird zuerst die Gleichung der so genannten Arbeitsgeraden ermittelt. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-31 In der rechten Masche der Schaltung in Bild 4.28 gilt: U Bat 2 = IC ⋅ R C + U CE (4.22) IC = (U Bat 2 − U CE ) / R C (4.23) Für die linke Masche kann geschrieben werden: U BE = U Bat1 (4.24) Gleichung 4.23 beschreibt die sog. Arbeitsgerade. Diese wird im Ausgangskennlinienfeld eingezeichnet. Die Schnittpunkte dieser Gerade mit den Kennlinien sind die möglichen Arbeitspunkte der Emitterschaltung. Die Gleichung 4.24 bestimmt die gültige Kennlinie aus dem Ausgangskennlinienfeld und legt somit den zu wählenden Schnittpunkt fest. Der Eingang der Emitterschaltung ist die Spannung, die zwischen den Anschlüssen BasisEmitter angelegt wird. Der Ausgang der Emitterschaltung ist die Spannung, die zwischen den Anschlüssen Kollektor und Emitter gemessen wird. Wird die Emitterschaltung als Verstärker benutzt, muss das Wechselstromsignal dem Eingangsgleichstromsignal überlagert werden. Dieser Zusammenhang ist im Bild 4.29 dargestellt. Die Wechselspannungsquelle ue(t) repräsentiert das Wechselstromsignal. Diese Schaltung ist die Grundschaltung eines Wechselstromverstärkers. Zur Ermittlung des Arbeitspunkts dieser Schaltung wird die Wechselspannungsquelle am Eingang kurzgeschlossen. Da die Schaltung linear ist, ist dies nach dem Überlagerungssatz zulässig. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-32 Bild 4.29 Emitterschaltung als Wechselstromverstärker – Anschauungsbild 4.4 Wechselstrom-Transistorverstärker In vielen Bereichen der Technik müssen Signale verstärkt werden. Einige Beispiele sind: Messtechnik: Verstärkung von Sensorsignalen (0 Hz bis einige MHz) Elektroakustik: Verstärkung von Tonfrequenzsignalen (20 Hz bis 20 kHz) Hochfrequenztechnik: Verstärkung von Antennensignalen (150 kHz bis einige GHz) Hierbei werden Transistorschaltungen eingesetzt und die Eigenschaft des Transistors als stromverstärkendes Bauelement genutzt. 4.4.1 Funktionsprinzip der Emitterschaltung als Verstärker Zur Veranschaulichung des Funktionsprinzips des Transistors als Signalverstärker wird die Emitterschaltung in Bild 4.30 mit einer veränderbaren Spannungsquelle UBat1 am Eingang und der konstanten Spannungsquelle UBat2 am Ausgang betrachtet. Bei der Quelle UBat1 wird zuerst eine Spannung in der Größenordnung der Diffusionsspannung des Basis-EmitterÜberganges (ca. 0.6 V) eingestellt. Dadurch wird zusammen mit der konstanten Spannungsquelle UBat2 und dem Widerstand RC ein Arbeitspunkt für den Transistor eingestellt. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-33 Bild 4.30 Emitterschaltung zur Veranschaulichung des Funktionsprinzips des Transistors als Signalverstärker Ausgehend von diesem Arbeitspunkt wird die Basis-Emitter-Spannung durch die Veränderung von UBat1 um einen kleinen ∆UBE erhöht. Dies führt zu einer Erhöhung des Basisstroms um den Betrag ∆I B und demzufolge auch zu einer Erhöhung des Kollektorstrom um den Betrag ∆Ic . Zur Ermittlung der Veränderung der Ausgangsspannung ∆UCE wird zunächst der Transistor im Bild 4.30 durch sein Gleichstrom-Ersatzschaltbild ersetzt (Bild 4.31). Bild 4.31 Emitterschaltung aus Bild 4.30 mit dem Transistor-Gleichstrom-Ersatzschaltbild Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-34 Im Schaltbild entsprechend Bild 4.31 werden für die Maschen I und II und den Knoten 1 die zugehörigen Kirchhoffschen Gleichungen aufgestellt: Masche I: UBE = R BE ⋅ IB + UBE0 (4.25) Masche II: R C ⋅ I C + U CE = U Bat 2 (4.26) Knoten 1: IC = IC0 + U CE R CE (4.27) Die Veränderung der Kollektor-Emitterspannung ∆UCE um den Arbeitspunkt wird durch die Variation der Parameter der Gleichungen 4.25 bis 4.27 bestimmt: ∆ U BE = R BE ⋅ ∆I B + ∆ U BE 0 aus 4.25 folgt: mit ∆U BE 0 = 0 : ∆U BE = R BE ⋅ ∆I B aus 4.26 folgt: R C ⋅ ∆IC + ∆U CE = ∆U Bat 2 mit ∆U Bat 2 = 0 : ∆U CE = − R C ⋅ ∆IC aus 4.27 folgt: ∆IC = ∆IC0 + mit ∆IC0 =β ∆I B Es ist somit: ∆IC = β⋅ ∆IB + (4.28) (4.29) ∆U CE R CE ∆UCE R CE (4.30) Gleichung (4.30) wird in Gleichung (4.29) eingesetzt: ⎛ R ∆U CE ⋅ ⎜1 + C ⎝ R CE ⎞ ⎟ = − R C ⋅β ⋅ ∆I B ⎠ (4.31) Nach einer Umformung ergibt sich für ∆UCE: ∆U CE = −β ⋅ 1 1 1 + R C R CE ⋅ ∆I B (4.32) Nun wird ∆I B in Gleichung (4.32) durch die Geichung (4.28) ersetzt, es ergibt sich für ∆UCE: ∆U CE = −β ⋅ 1 1 1 + R C R CE ⋅ ∆U BE R BE Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-35 Mit ∆UCE = ∆Ua und ∆UBE = ∆Ue folgt: ∆U a = −β ⋅ ∆U e 1 ⎛ 1 1 ⎞ R BE ⋅ ⎜ + ⎟ ⎝ R C R CE ⎠ (4.33) Mit der Vereinfachung R CE ≈ ∞ ergibt sich: ∆U a R ≈ −β⋅ C ∆U e R BE (4.34) Es ist zu erkennen, dass der Betrag von ∆UCE um den Faktor β ⋅ RC größer ist als ∆UBE. R BE Allerdings bewirkt, durch das negative Vorzeichen bedingt, eine positive Abweichung ∆UBE eine negative Abweichung um ∆UCE vom Arbeitspunkt. 4.4.2 Wechselstromverstärker in Emitterschaltung Im Folgenden wird ein einstufiger Wechselspannungs-Verstärker mit einem Bipolartransistor untersucht. Dabei werden die prinzipiellen Merkmale von Verstärkerschaltungen hergeleitet, die auch für andere Arten von elektronischen Verstärkern von Bedeutung sind. Als Beispiel sei die einfache Verstärkerstufe in Emitterschaltung vorgegeben (Bild 4.32). Bei der im Bild 4.32 dargestellten Wechselstromverstärkerschaltung erfolgt die Einstellung des Transistor-Arbeitspunkts über die Spannungsquelle UBat2 und den Widerstand R1. Außerdem wird das Wechselstromsignal über die Eingangskapazität Ce in die Schaltung „eingekoppelt“ und über die Ausgangskapazität Ca wieder „ausgekoppelt“. Dadurch wird gewährleistet, dass der Schaltung reine Wechselstromsignale zugeführt bzw. von der Schaltung abgeführt werden. Ferner wird die Wechselspannungsquelle (Signalquelle) vor der Gleichspannungsquelle geschützt (getrennt). Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-36 Bild 4.32 Einstufiger Wechselstromverstärker in Emitterschaltung Zur Analyse der Schaltung werden folgende Vereinfachungen angenommen: 1. Der Kollektor-Emitter-Widerstand RCE ist unendlich groß. 2. Die Sperrschichtkapazitäten CBC und CBE sind sehr klein, sodass ihre Wirkung für den mittleren Frequenzbereich vernachlässigt werden kann. 3. Die Kapazitäten Ce und Ca sind sehr groß und leiten auch bei sehr kleinen Frequenzen den Wechselstrom durch. Die Annahmen 1 und 2 führen zu den vereinfachten Transistorersatzschaltbildern Bild 4.33 und Bild 4.34. Die Annahme 3 bezieht sich auf die gesamte Schaltung, in der die Kapazitäten Ce und Ca für die Wechselstrombetrachtung als kurzgeschlossen betrachtet werden können. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-37 Bild 4.33 Vereinfachtes Transisitor-Gleichstrom-Ersatzschaltbild Bild 4.34 Vereinfachtes Transisitor-Wechselstrom-Ersatzschaltbild Zur Ermittlung einer Beziehung zwischen der Eingangs- und Ausgangsspannung des Wechselstromverstärkers wird die Schaltung aus Bild 4.32 genauer betrachtet: In dem vorgestellten Wechselstromverstärker sind zwei Spannungsquellen vorhanden: die Wechselspannungsquelle ue(t) und die Gleichspannungsquelle UBat2. Die verschiedenen Transistorersatzschaltbilder zeigen, dass das Verhalten des Transistors bezüglich des Wechselstroms und des Gleichstroms verschieden ist. Da es sich bei den ermittelten Transistorersatzschaltbildern um lineare Schaltungen handelt (durch Linearisierung gewonnen), bietet sich die Anwendung des Überlagerungsprinzips als die geeignete Methode zur Analyse der Wechselstromverstärker-Schaltung an. Die Berechnung des Wechselstromverstärkers erfolgt deshalb in zwei Schritten. Im ersten Schritt wird die Wechselspannungsquelle kurzgeschlossen, die Gleichstromparameter werden berechnet und der Arbeitspunkt wird eingestellt. Im zweiten Schritt wird die Gleichspannungsquelle kurzgeschlossen und die Wechselstromparameter werden berechnet. Die Überlagerung beider Ergebnisse liefert die Werte der Mischsignale in der realen Schaltung. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-38 Schritt 1: Gleichstrombetrachtung – Einstellung des Arbeitspunkts Die Wechselspannungsquelle, die die Eingangsspannung (Signalspannung) der Schaltung ist, wird kurzgeschlossen, d. h. es wird zunächst ue(t) = 0 gemacht. Es treten jetzt nur noch Gleichgrößen in der Schaltung auf. Der Transistor wird nun durch das Ersatzschaltbild entsprechend Bild 4.33 dargestellt, welches nur die für Gleichstrom relevanten Größen enthält. Die gesamte Schaltung wird aus der Gleichspannungsquelle UBat versorgt. Durch entsprechende Wahl der Widerstände R1 und RC wird erreicht, dass sich die gewünschten Parameter des Arbeitspunkts einstellen und die Verlustleistung des Transistors PV ≈ UCE IC im zulässigen Bereich liegt. Dieses Verfahren (Schritt 1) wird als Einstellung des Arbeitspunkts bezeichnet. Durch den Kurzschluss der Wechselspannungsquelle ue(t) und unter Einsatz des TransistorGleichstromersatzschaltbildes wird das Gleichstromersatzschaltbild der Verstärkerschaltung (Bild 4.35) ermittelt. Bild 4.35 Gleichstrombetrachtung des Wechselstromverstärkers – Berechnung des Arbeitspunkts mit dem Gleichstromersatzschaltbild Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-39 Die Schaltung kann nun mit Hilfe der Kirchhoffschen Gesetze und der Stromverstärkungsgleichung berechnet werden: Zweige: z = 3, Knoten: k = 2 => unabhängige Knotengleichungen: n = k – 1 = 1 Knoten 1: I Bat = I B + I C (4.35) unabhängige Maschengleichungen: m = z – (k – 1) = 2 Masche I: U BE0 + I B ⋅ R1 + I B ⋅ R BE − U Bat = 0 (4.36) Masche II: U CE + IC ⋅ R C − U Bat = 0 (4.37) Stromverstärkung: IC = B ⋅ I B (4.38) Die Dimensionierung der Widerstände für einen Arbeitspunkt mit UCE = UBat/2 (der gewählte Wert für UCE wird später begründet) und einen Strom IC ergibt: RC = U Bat 2 ⋅ IC R1 = B ⋅ (4.39) U Bat − U BE0 − R BE IC (4.40) Schritt 2: Wechselstrombetrachtung – Berechnung des Verstärkungsfaktors Nun wird am Eingang der Schaltung eine Wechselspannung ue(t) = ûe.sin(ωt) angelegt. Wie bereits erläutert, da der Transistor um den Arbeitspunkt als lineares Bauelement modelliert wird, darf der Überlagerungssatz angewendet werden. D.h. das Wechselstromverhalten kann dann unabhängig vom bereits ermittelten Gleichstromverhalten berechnet werden. Dazu wird die Gleichspannungsquelle kurzgeschlossen, d.h. es gilt UBat = 0 und der Transistor wird durch sein Wechselstrom-Ersatzschaltbild (Bild 4.34) ersetzt. Es ergibt sich die Schaltung entsprechend Bild 4.36. Die Wechselstromanalyse dient zur Berechnung der Verstärkung der Schaltung. Zur Berechnung der Spannungsverstärkung vu wird die Beziehung zwischen ue(t) und ua(t) ermittelt. Dabei wird derjenige Wert für ua(t) angenommen, der sich einstellt, wenn kein Ausgangsstrom fließt (die so genannte Leerlaufspannung). Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-40 Zur Berechnung der Stromverstärkung vi wird die Beziehung zwischen ie(t) und ia(t) ermittelt. Dabei wird der jenige Wert für ia(t) eingesetzt, bei dem der (Wechselstrom-) Ausgang kurzgeschlossen ist. Da in der Schaltung entsprechend Bild 4.36 aufgrund der möglichen Vereinfachungen keine Kapazitäten vorhanden sind, kann die Analyse der Schaltung mit zeitabhängigen Größen erfolgen. Anderenfalls bietet sich die Berechnung der Schaltung mit komplexen Größen als weniger aufwändig an. Bild 4.36 Wechselstrombetrachtung des Wechselstromverstärkers – Berechnung der Verstärkungsfaktoren mit dem Wechselstromersatzschaltbild Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-41 Für den Eingangskreis gilt: u BE ( t ) = u e ( t ) = i B ( t ) ⋅ R BE (4.41) Für den Ausgangskreis gilt: u CE ( t ) = u a ( t ) = − R c ⋅ i RC ( t ) (4.42) da ia ( t ) = 0 vorausgesetzt wird, gilt: i RC ( t ) = i C ( t ) = β ⋅ i B ( t ) (4.43) Die Gleichungen 4.42 und 4.43 ergeben: u a ( t ) = − R C ⋅ i c ( t ) = − R C ⋅β ⋅ i B ( t ) (4.44) Die Gleichungen 4.44 und 4.41 ergeben: ua ( t ) = − RC ⋅β⋅ u e ( t ) R BE (4.45) ua ( t ) = vU ⋅ u e ( t ) v u = −β ⋅ (4.46) RC R BE (4.47) Die Spannungsverstärkung vu beschreibt die Beziehung zwischen der Eingangswechselspannung ue(t) und der Ausgangswechselspannung ua(t) (im Leerlauf). Das negative Vorzeichen in Gleichung 4.47 bedeutet, dass die Phasenlage der Ausgangsspannung gegenüber der Eingangsspannung um 180° verschoben ist. Zur Berechnung der Stromverstärkung vi wird im Wechselstromersatzschaltbild des Verstärkers der Ausgangsstrom bei kurzgeschlossenen Ausgangsklemmen berechnet: ia ( t ) = iC ( t ) = β ⋅ i B ( t ) (4.48) Aus dem Eingangskreis unter Verwendung der Stromteilerregel wird ermittelt: i B ( t ) = ie ( t ) ⋅ R1 R1 + R BE Einführung in die Elektrotechnik Teil II (4.49) Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-42 Gleichung 4.48 wird in Gleichung 4.47 eingesetzt: i C ( t ) = i e ( t ) ⋅β ⋅ R1 R1 + R BE (4.50) i a ( t ) = vi ⋅ i e ( t ) (4.51) Der Stromverstärkungsfaktor vi beträgt somit: vi = β ⋅ R1 R1 + R BE (4.52) Vereinfachend gilt: vi = β (4.53) Die Näherung ist meist zulässig, da RBE i.A. um 3 Größenordnungen kleiner ist als R1. Die Leistungsverstärkung vP ergibt sich als Betrag des Produkts aus Strom- und Spannungsverstärkung: v p = v u ⋅ vi Anmerkung 5: (4.54) Komplexe Verstärkungsfaktoren Es ist anzumerken, dass im Allgemeinen die Verstärkungsfaktoren komplexe Größen sind und Terme beinhalten, die den Einfluss der Kapazitäten, die hier vernachlässigt wurden, beschreiben. Zum Beispiel kann die Gleichung 4.47 auch wie folgt in komplexer Form geschrieben werden: vu = Ua Ue Vu = β ⋅ (4.55) R c ± j⋅π ⋅e R BE Anmerkung 6: (4.56) Verhalten eines Verstärkers bei mittlerer Frequenz Würde die Wechselstromverstärkerschaltung vollständig und unter Berücksichtigung der Kapazitäten berechnet werden, ergäben sich zwei Grenzfrequenzen für den Betrieb des Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-43 Wechselstromverstärkers: Die obere Grenzfrequenz fo bzw. die obere Grenzkreisfrequenz ω0 und die untere Grenzfrequenz fu. bzw. die untere Grenzkreisfrequenz ωu. Die obere Grenzfrequenz wird durch den Kollektorwiderstand RC und und die BasisKollektorkapazität CBC (transistorspezifisch) bestimmt: ωO = 1 R C ⋅ C BC (4.57) 1 R e ⋅ Ce (4.58) R1 ⋅ R BE R1 + R BE (4.59) und ωu = mit Re = In der Praxis werden diese Frequenzen für einen gegebenen Transistor und seine Schaltung mit den obigen Formeln berechnet. Befindet sich die gewählte Arbeitsfrequenz innerhalb dieser Grenzen, so kann der Einfluss der Kapazitäten vernachlässigt werden und die Verstärkungen nach den Gleichungen 4.47 und 4.53 ermittelt werden. 4.4.3 Arbeitsgerade und Aussteuerbarkeit von Verstärkern Wechselspannungs-Verstärker sollen die verfügbare Speisespannung gut ausnutzen. Die gesamte Ausgangsspannung ua = UCEA + ûa . sin(ωt) darf die Versorgungs-Gleichspannung UBat weder über- noch unterschreiten. Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-44 Bild 4.37 Einfluss der Arbeitspunkteinstellung auf die Ausgangskurvenform bei hoher Aussteuerung Um eine maximale Aussteuerbarkeit zu gewährleisten, ist es sinnvoll, den Arbeitspunkt bei etwa UCE = UBat/2 zu wählen. Die zulässige maximale Amplitude der Ausgangsspannung beträgt dann ûa = UBat/2. 4.4.4 Ersatzschaltbild des Wechselstromverstärkers Das Gesamtverhalten eines Wechselstrom-Verstärkers innerhalb des mittleren Frequenzbereichs kann vereinfacht durch das Ersatzschaltbild im Bild 4.38 charakterisiert werden. Bild 4.38 Ersatzschaltbild eines Wechselstromverstärkers Einführung in die Elektrotechnik Teil II Kapitel 4: Halbleiterelektronik – Bipolartransistor 4-45 Werden in den Ersatzschaltbildern Kapazitäten berücksichtigt, so treten Ausgangs- und Eingangsimpedanzen auf. Da im Bild 4.38 die Kapazitäten nicht berücksichtigt wurden, treten hier rein reelle Ein- und Ausgangsimpedanzen (ohmsche Widerstände) auf. Der Eingangswiderstand des im Bild 4.32 vorgestellten Verstärkers wird anhand des Wechselstromersatzschaltbildes (Bild 4.36) wie folgt berechnet: Re = U e R1 ⋅ R B = Ie R1 + R B (4.60) Der Ausgangswiderstand ist der Innenwiderstand der Ausgangsspannungsquelle. Für die Schaltung entsprechend Bild 4.32 ist er gegeben durch: Ra = Ua 0 vu ⋅ Ue = = Rc Iak Ic Einführung in die Elektrotechnik Teil II (4.61) Kapitel 4: Halbleiterelektronik – Bipolartransistor