1. Kennlinien 2. Stabilisierung der Emitterschaltung

Schaltungstechnik 2
Übung 4
1. Kennlinien
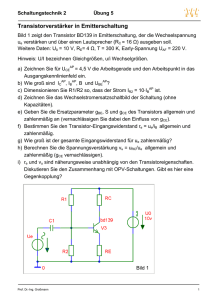
Der Transistor BC550C soll auf den Arbeitspunkt UCE = 4 V und IC = 15 mA
eingestellt werden.
a) Bestimmen Sie aus den Kennlinien (S. 2) die Werte für IB, B, UBE.
b) Woher kommt die Neigung der Ausgangskennlinien?
c) Bestimmen Sie die Early-Spannung UAF.
d) Was passiert bei kleinem UCE (starker Anstieg)?
2. Stabilisierung der Emitterschaltung
Die Transistorschaltung in Bild 1 (Emitterschaltung) soll auf den Arbeitspunkt
UCE = 5 V eingestellt werden. Der Kollektorwiderstand (Last) ist RC = 250 Ω.
a) Dimensionieren Sie den Basis-Spannungsteiler entsprechend. Bestimmen Sie
dazu zuerst IC, IB und UBE.
b) Wie muss R2 geändert werden, damit IC um 20% sinkt? Welche Folgerung
ergibt sich für die Stabilität des Arbeitspunktes?
Nun untersuchen Sie die Schaltung in Bild 2, wobei RC = 200 Ω und RE = 50 Ω. Es
soll wieder der Arbeitspunkt UCE = 5 V eingestellt werden.
Bild 1
Bild 2
c) Dimensionieren Sie wieder den Basis-Spannungsteiler.
d) Wie muss nun R2 geändert werden, damit IC um 20% sinkt? Was ergibt sich für
die Stabilität des Arbeitspunktes im Vergleich zu b)?
Prof. Dr.-Ing. Großmann
1
Schaltungstechnik 2
Übung 4
BC550C: Kennlinien
1.0mA
100uA
10uA
1.0uA
100nA
10nA
500mV
Ib(V1)
550mV
600mV
650mV
700mV
750mV
800mV
Eingangskennlinie
V_Ube
45mA
IB = 80 µA
40mA
35mA
30mA
IB = 50 µA
25mA
20mA
15mA
IB = 20 µA
10mA
IB = 10 µA
5mA
0A
0V
1V
2V
3V
4V
5V
6V
7V
8V
9V
10V
Ic(V1)
V_Uce
Prof. Dr.-Ing. Großmann
Ausgangskennlinienfeld
2
Schaltungstechnik 2
Übung 4
1.a) 1. Arbeitspunkt einzeichnen auf Ausgangskennlinie: ICAP = 15 mA, UCEAP = 4 V
2. dazugehörige Kennlinie hat den Parameter IB = 30 µA
3. in Eingangskennlinie: aus IB = 30 µA
UBE ≈ 733 mV
folgt
4. B = IC/IB = 15 mA / 30 µA = 500
297uA
Ausgangskennlinienfeld
40mA
Eingangskennlinie
100uA
IB=30 µA
20mA
IB=30 µA
10uA
UBE=733 mV
2.4uA
0A
0V
2V
4V
6V
8V
Ic(V2)
10V
680mV
Ib(V1)
700mV
720mV
740mV
760mV
780mV
V_Ube
V_U2
b) Basisweitenmodulation: Der Diffusionsstrom hängt ab von der Weite dB der (neutralen) Basis. Wenn
sich mit der Spannung UCE die Weite der beiden Raumladungszonen (RLZ) ändert, ändert sich auch die
Weite dB. Der größte Teil von UCE liegt dabei als Sperrspannung UCB an der Kollektor-Basis-Strecke,
während an der Basis-Emitter-Strecke die Spannung in Flussrichtung meist nur zwischen 0,7 bis 0,8 V
schwankt (für Silizium; bei Germanium um 0,3 V). Mit steigendem UCE wird die Sperrspannung UBC
größer, damit auch die Weite dieser RLZ, also sinkt die Basisweite. Der Diffusionsstrom steigt an, weil
die Änderung der Minoritäts-Ladungsträgerdichte in der Basis steiler wird.
In der Ausgangskennlinie IC(UCE) kann man diesen Effekt durch den Faktor 1 berücksichtigen,
wobei mit UAF die (positive) Early-Spannung bezeichnet ist, die für jeden Transistor ein typischer
Parameter und häufig im Datenblatt zu finden ist.
c) UAF kann aus der Neigung jeder beliebigen Ausgangskennlinie bestimmt werden. Aus der Geometrie
(s. Bild) folgt die Beziehung
∆IC
IC
∆UCE
-UAF
UCE
Δ Δ
Z.B. für die Kennlinie zu IB = 80 µA lesen wir zwei Punkte
ab: { 2 V; 32 mA } und { 9 V; 41 mA }. Also ist
778 Ω # 32 &' ( 2 ) 22,9 ).
d) Annahme: UCE ≈ 0. Wenn IB > 0, dann muss UBE ≈ 0,7 V sein. Dann ist UCB = UCE-UBE ≈ -0,7 V. Damit
ist die Basis-Kollektor-Strecke in Flussrichtung gepolt (Sättigungsbetrieb), entgegen den sonstigen
Betrachtungen. In diesem Fall werden die Elektronen nicht oder nur schwach zum Kollektor gesaugt und
der Diffusionsstrom IC ändert sich stark mit UCB, also auch mit UCE. Erst wenn UCB > 0 gilt, funktioniert
das Absaugen und der Diffusionsstrom ändert sich mit UCE nur noch wenig.
Prof. Dr.-Ing. Großmann
3
795mV
Schaltungstechnik 2
Übung 4
2. a) Strom und Spannung im Arbeitspunkt (2 Variablen) lassen sich aus 2 Gleichungen bestimmen.
Grafisch kann man jede Gleichung als Kurve im Spannungs-Strom-Diagramm darstellen. Der
Schnittpunkt ist die Lösung des Gleichungssystems.
Die erste Gleichung ist die nichtlineare Ausgangskennlinie IC(UCE) des Transistors. Die zweite Gleichung
ist die Ausgangs-Maschengleichung: , # - . . Diese Gleichung wird so
umgeformt, dass man sie direkt in das Kennlinien-Diagramm einzeichnen kann: / ,
.
Das ist die Gleichung der Arbeitsgeraden. Sie enthält unter anderem 3 Punkte: {IC=0; UCE=U0} ,
{IC=U0/RC; UCE=0} und den Arbeitspunkt {ICAP; UCEAP} . Zur Lösung der gestellten Aufgabe gehen wir
folgendermaßen vor:
40mA
40 µA
a),c)
20mA
30 µA
b),d)
1. Aus unseren Angaben hier können wir die
Arbeitsgerade durch die beiden ersten
Punkte eindeutig zeichnen (U0/RC = 40 mA).
Mit der zusätzlichen Angabe UCEAP = 5 V
ergibt sich der Strom ICAP = 20 mA.
2. Für die zugehörige Transistor-Kennlinie
ist IBAP = 40 µA.
3. Aus der Eingangskennlinie ergibt sich
UBE(IB=40 µA) = 0,74 V. Diese Spannung
V_U2
soll mit dem Basis-Spannungsteiler R1/R2
eingestellt werden; dazu gibt es beliebig viele Lösungen. Achtung: Der Spannungsteiler ist belastet, es
wird der Strom IB abgezogen!
0A
0V
2V
4V
6V
8V
10V
Ic(V2)
4. Ohne weitere Angaben gehen wir von der Daumenregel IR2 ≈ 10#IB aus. Damit ist der Effekt des
Basisstroms auf den Spannungsteiler klein, andererseits sind die Widerstände R1, R2 noch so groß, dass
sie eine angeschlossene Signalquelle nicht zu stark belasten.
Wir kennen nun die Spannung an R2 (UBE = 0,74 V) und den Strom durch R2 (IR2 = 10#40µA), also ist
.,0 - .. 1 1850 Ω.
5. Für die Eingangsmasche gilt: , , .
, . ( , 10 ) ( 0,74 ) 9,26 ).
,6 Der Strom durch R1 besteht aus IR2 + IB = 440 µA. Damit ist - . 1 21045 Ω.
b) Hier geht es um die Stabilität des Arbeitspunktes: Welchen Einfluss hat eine Änderung des BasisSpannungsteilers z.B. durch Bauteiltoleranzen oder Temperaturänderung? Um dies abzuschätzen,
rechnen wir rückwärts, welche Änderung z.B. von R2 eine Änderung von IC um -20 % bewirkt.
Die Vorgehensweise ist ähnlich wie in a):
1.: Wir gehen von der gleichen Arbeitsgeraden aus, da weder U0 noch RC sich ändern. Aber wir geben
nun vor ICAP = 0,8#20 mA = 16 mA. Daraus folgt UCEAP = 6 V.
2., 3.: IBAP = 30 µA und damit UBEAP = 0,733 V
4.: Die Forderung IR2 = 10#IB können wir nicht mehr aufrecht erhalten, weil R1 gleich bleibt. Den Strom
durch R2 müssen wir „hinnehmen, wie er kommt“. Die Spannung an R2 ist UBE = 0,733 V, für UR1 bleiben
noch 10 V – 0,733 V = 9,27 V. Da R1 = 21045 Ω gleich bleibt, ist IR1 = 9,26 V / 21045 Ω = 440 µA.
Prof. Dr.-Ing. Großmann
4
Schaltungstechnik 2
Übung 4
5.: Von IR1 wird IB = 30 µA abgezogen, der Rest ist IR2 = 440 µA – 30 µA = 410 µA der Strom durch R2.
Der neue Wert ist also - 7
89:
.,0 . 1
1788 Ω. Das entspricht einer relativen Änderung von -3,4 %.
Andersherum betrachtet führt also eine Änderung von 3,4 % am Eingang zu einer Änderung von 20 %
am Ausgang. Der so eingestellte Arbeitspunkt ist nicht besonders stabil.
Das soll sich nun mit einem Emitterwiderstand RE verbessern. Die Ausgangsmasche, die die
Arbeitsgerade definiert, ist nun , , # ;- - < . .
Da RC+RE = 250 Ω weiterhin gilt, ändert sich unsere Arbeitsgerade hier nicht. Es ergeben sich die
gleichen Arbeitspunkte wie in a) bzw. b) (Schritte 1-3).
c) Schritt 4: wir dürfen wieder fordern IR2 = 10#IB = 400 µA.
Es gilt nun UR2 = UBE + IC#RE = 0,74 V + 20 mA # 50Ω = 1,74 V und damit R2 = 1,74 V/400 mA = 4350 Ω.
Schritt 5: UR1 = 10 V – 1,74 V = 8,26 V und IR1 = 440 µA, damit R1 = 18773 Ω.
d) Schritt 4: IR2 ergibt sich wieder aus anderen Bedingungen (R1 = 18773 Ω). Es ist
UR2 = UBE + IC#RE = 0,733 V + 16 mA # 50Ω = 1,533 V → UR1 = 10 V – 1,533 V = 8,467 V →
IR1 = 451 µA
Schritt 5: IR2 = 451 µA – 30 µA = 421 µA, R2 = 1,533 V / 421 µA = 3641 Ω. Das entspricht einer relativen
Änderung um -16,3 %.
Mit Emitterwiderstand führt also erst eine Änderung am Eingang um 16,3% zu einem Ausgangsfehler
von 20 %; das liegt in der gleichen Größenordnung. Der Arbeitspunkt ist deutlich stabiler als ohne
Emitterwiderstand.
Prof. Dr.-Ing. Großmann
5