Transistorverstärker in Emitterschaltung

Schaltungstechnik 2
Übung 5
Transistorverstärker in Emitterschaltung
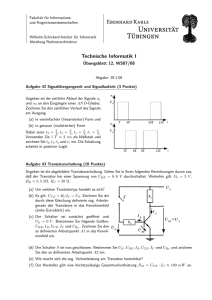
Bild 1 zeigt den Transistor BD139 in Emitterschaltung, der die Wechselspannung
ue verstärken und über einen Lautsprecher (RC = 16 Ω) ausgeben soll.
Weitere Daten: U0 = 10 V, RE= 4 Ω, T = 300 K, Early-Spannung UAF = 220 V.
Hinweis: U/I bezeichnen Gleichgrößen, u/i Wechselgrößen.
a) Zeichnen Sie für UCEAP = 4,5 V die Arbeitsgerade und den Arbeitspunkt in das
Ausgangskennlinienfeld ein.
b) Wie groß sind ICAP, IBAP, B und UBEAP?
c) Dimensionieren Sie R1/R2 so, dass der Strom IR2 = 10⋅IBAP ist.
d) Zeichnen Sie das Wechselstromersatzschaltbild der Schaltung (ohne
Kapazitäten).
e) Geben Sie die Ersatzparameter gBE, S und gCE des Transistors allgemein und
zahlenmäßig an (vernachlässigen Sie dabei den Einfluss von gCE).
f) Bestimmen Sie den Transistor-Eingangswiderstand re = ue/iB allgemein und
zahlenmäßig.
g) Wie groß ist der gesamte Eingangswiderstand für ue zahlenmäßig?
h) Berechnen Sie die Spannungsverstärkung vu = uRC/ue allgemein und
zahlenmäßig (gCE vernachlässigen).
i) re und vu sind näherungsweise unabhängig von den Transistoreigenschaften.
Diskutieren Sie den Zusammenhang mit OPV-Schaltungen. Gibt es hier eine
Gegenkopplung?
Bild 1
Prof. Dr.-Ing. Großmann
1
Schaltungstechnik 2
Übung 5
j) Der Lautsprecher gibt nur Frequenzen über fmin = 500 Hz unverzerrt wieder.
Berechnen Sie C1 so dass die untere Grenzfrequenz des Verstärkers fmin wird.
Nun wird ein Kondensator CE = 1000 µF parallel zu RE geschaltet.
k) Bestimmen Sie den neuen Transistor-Eingangswiderstand re´ sowie die neue
Spannungsverstärkung vu´. Welche Vorteile/Nachteile hat CE?
l) Zeichnen Sie die Wechselstrom-Arbeitsgerade ins Kennlinienfeld ein.
CE wird nun wieder entfernt.
m) Berechnen Sie die Gleich- und die Wechselleistung des Transistors für eine
Eingangsamplitude von ûe = 1 V.
n) Auf welcher Temperatur befindet sich die Sperrschicht ohne Kühlkörper bzw.
mit Kühlkörper? Rth,JAmb = 110 K/W, Rth,JCase = 10 K/W, Rth,Kühlk = 15 K/W.
Prof. Dr.-Ing. Großmann
2
Schaltungstechnik 2
Übung 5
BD139: Kennlinien
12mA
10mA
8mA
6mA
4mA
IB = 2,5 mA
2mA
0A
600mV
Ib(V3)
650mV
700mV
750mV
800mV
850mV
900mV
950mV
Eingangskennlinie
V(V3:b)
IB = 10 mA
800mA
700mA
600mA
IB = 5 mA
WS-Arbeitsgerade
500mA
400mA
IB = 3 mA
300mA
IB ≈ 2,5 mA
ICAP
200mA
IB = 1 mA
100mA
IB = 0 mA
0A
0V
1V
Ic(V3)
2V
3V
4V
UCE
AP 5V
V_Uce
Prof. Dr.-Ing. Großmann
6V
7V
8V
9V
10V
Ausgangskennlinienfeld
3
Schaltungstechnik 2
Übung 5
a) Die Ausgangsmasche definiert wieder die Arbeitsgerade:
⋅ . Zwei Punkte können wir angeben:
{IC=0; UCE=U0=10 V} und {IC=U0/(RC+RE)=500 mA; UCE=0}. Der Arbeitspunkt
ergibt sich aus UCEAP = 4,5 V.
b) abgelesen: 270 ; 2,5 ;
,
108; 0,8 c) R2 = UR2/IR2 mit IR2 = 25 mA (Forderung aus Angabe)
⋅ 0,8 0,27 ⋅ 4Ω 1,88 → R2 = 75,2 Ω
R1 = UR1/IR1 mit IR1 = IR2+IB = 27,5 mA und UR1 = U0-UR2=8,12 V →
R1 = 295 Ω
d) für Wechselströme stellt eine ideale Gleichspannungsquelle (z.B. U0) einen
Kurzschluss dar (Gleichstromquellen sind dann Unterbrechungen).
Wechselstrommäßig hängen R1 und RC damit direkt an Masse:
gCE
B
uE
iB
~
E
C
iT
rBE
" # $ ⋅ % ⋅ "
uRC
R1
RE
R2
RC
e) aus den idealen Transistorgleichungen:
)*
'(
& & $
+,
, -
. -/
'1)*
)* 3+
+12
)4
'1)*
+,
⋅
)*
'(
+,
0 0,1 $
-
5, /
(entspricht 10 Ω)
1,2 $
(entspricht 830 Ω)
⋅ & 0 10 $
Anmerkung: Aus der Eingangskennlinie kann man ein gBE ≈ 0,04 S ablesen. Die
Abweichung zur Theorie lässt sich durch technologische Besonderheiten des
Leistungstransistors erklären. Für andere Transistortypen passt die Theorie
besser, deshalb üben wir mit gBE = 0,1 S weiter.
Vernachlässigung von gCE: Da 1/ gCE ≫ RE, RC, 1/ gBE gilt, kann es für die weiteren
Teilaufgaben vernachlässigt werden.
Prof. Dr.-Ing. Großmann
4
Schaltungstechnik 2
Übung 5
f) Achtung: Der Transistor-Eingangswiderstand 78 %8 /" enthält nicht die
Spannungsteiler-Widerstände R1 und R2. Diese werden in g) berücksichtigt.
%8 % % 0
" ⋅ <
=
78 =
;(2
?
:(
;(2
" " # ⋅ 1 ⋅ >
;(2
1 ⋅ 10 Ω 436 Ω
0 ⋅ 446 Ω
Die letzte Näherung gilt, weil B ≫ 1 und ⋅ ≫
=
;(2
.
g) Die Quelle wird belastet durch die Parallelschaltung von
Rges = = B
B78 0 53 Ω.
h) % " ⋅ 0 " # ⋅ ⋅ " ⋅ ?
CF1
CD
⋅
1
ED
3,9
mit der Näherung 78 0 ⋅ wird
CF1
CD
CD
ED
0
⋅ ⋅ ⋅1
⋅2
1
2
4
i) Gegenkopplung macht eine Schaltung unabhängig von den
Verstärkereigenschaften. Ein OPV hat eine sehr große Spannungsverstärkung,
der Transistor immerhin eine große Stromverstärkung. Gegenkopplung stabilisiert
(siehe Übung 4), aber sie verringert die Verstärkung.
Hier liegt eine sogenannte Stromgegenkopplung durch RE vor:
Wenn IT ≈ IRC steigt, wird auch URE größer. Da durch den Basis-Spannungsteiler
die Spannung UR2 ≈ const, wird UBE = UR2 – URE kleiner. Damit sinkt IB und in folge
auch IC. Der Arbeitspunkt wird stabilisiert.
j) Grenzkreisfrequenz HI =
JDK ⋅L
2M ⋅ 500 NO → P= =
QR ⋅JDK
6 μT
k) Durch CE wird RE für Wechselströme kurzgeschlossen (der Arbeitspunkt bleibt
erhalten). In den Formeln für re und vU setzen wir RE = 0 und erhalten
78 ´ =
;(2
Vorteil:
10 Ω
und
V+ ´ ⋅ ⋅ & 170
Verstärkung wird größer
Nachteil: Eingangswiderstand sinkt, Quelle wird stärker belastet
Prof. Dr.-Ing. Großmann
5
Schaltungstechnik 2
Übung 5
l) Die Wechselstrom-Arbeitsgerade läuft auch durch den Arbeitspunkt, ihre
Steigung beträgt aber -1/RC, sie ist deshalb steiler als die GleichstromArbeitsgerade mit Steigung -1/(RC+RE).
Der Schnittpunkt mit IC = 0 liegt bei UCE = 8,92 V. Die restlichen 1,08 V bis zur
Betriebsspannung U0 liegen als Arbeitspunkt-Gleichspannung an RE an, sie
stehen nicht für Wechselspannungen zur Verfügung.
m) Da die Spannung UCE > 0 ist und der Strom IC > 0 und beide die gleiche
Orientierung haben, stellt der Transistor gleichstrommäßig einen Verbraucher dar.
Die Gleichleistung im Arbeitspunkt beträgt
WX ⋅ 4,5 ⋅ 0,27 1,2 Y
Wechselspannungsmäßig stellt der Transistor eine Stromquelle dar, die i.a.
Leistung abgibt. Die Wechselspannungs-Amplitude ûCE ist
%Z [%Z %Z [\̂ # ⋅ mit
\̂ # ⋅ \̂ ⋅
^D
C
ED
108 ⋅
=/
55. Ω
0,242 und die Wechselleistung ist
=
=
W~ ⋅ %Z ⋅ \̂ # [ ⋅ \̂# ⋅ [
,5` ⋅
Y [0,58 Y
n) Die Gesamtleistung ist W;8a WX W~ 1,2 Y [ 0,58 Y 0,62 Y. Das ist die
Leistung, die vom Transistor in Wärme umgesetzt wird.
ohne Kühlkörper ist Δc W;8a ⋅ de,f-g 68 h → ϑJ 95 °C
mit Kühlkörper ist Δc W;8a ⋅ m
de,fna8 de,oüeqr s 15,5 h → ϑJ 42,5 °C
Prof. Dr.-Ing. Großmann
6