Lösungsvorschlag

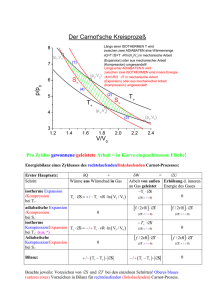
Karlsruher Institut für Technologie
Institut für Theorie
der Kondensierten Materie
Übungen zur Theoretischen Physik F
SS 2016
Blatt 2
Lösungsvorschlag
Prof. Dr. A. Shnirman
Dr. B. Narozhny, Dipl.-Phys. P. Schad
1. Ideales Boltzmann-Gas:
(8+10+2+5=25 Punkte, schriftlich)
Die innere Energie eines idealen einatomigen Boltzmann-Gases beträgt U = 3N kB T /2,
wobei die Zustandsgleichung pV = N kB T lautet. Hierbei bezeichnet N die Zahl der
Atome, T die Temperatur, p den Druck und V das Volumen des Systems.
(a) Berechnen Sie die Entropie des Systems S(T, V ) als Funktion der Temperatur und
des Volumens indem Sie von der inneren Energie ausgehen. Bestimmen Sie die freie
Energie F (T, V ).
Wir berechnen zunächst die Entropie. Bei konstanter Teilchenzahl N ist das totale
Differential der Entropie S(T, V )
∂S ∂S dT
+
(1)
dS =
dV
∂T V
∂V T
Aus dem ersten Hauptsatz ergibt sich zusammen mit der thermodynamischen Definition dS = δQ/T der Entropie bei konstanter Teichenzahl N die Relation
dU = T dS − pdV.
(2)
Für das ideale Gas können wir auf der linken Seite dU = 23 N kB dT einsetzen.
Auflösen von Gl. (2) nach dS und Vergleich mit Gl. (1) ergibt dann
3N kB
∂S (3)
=
∂T V
2T
p(V, T )
N kB
∂S =
(4)
=
∂V T
T
V
Wir integrieren Gl. (3) und erhalten
3
T
S(T, V ) = N kB ln
+ α(V )
2
T0
(5)
mit einer unbekannten Funktion α(V ) und einem beliebigen Referenztemperatur
T0 . Die Funktion α(V ) bestimmen wir mit Gl.(4) und finden das Ergebnis
T
V
3
S(T, V ) = N kB ln
+ N kB ln
= N kB ln V T 3/2 + C0
2
T0
V0
(6)
Die Beitrge der Referenzgrößen wurden zu einem konstanten Beitrag C0 zusammengefasst. Im Allgemeinen, d.h. bei variabler Teilchenzahl N , ist die unbekannte
Konstante C0 eine Funktion von N . Bei konstanter Teilchenzahl ist diese Konstante
für die Thermodynamik irrelevant.
Die freie Energie folgt direkt aus F (T, V ) = U (T, V ) − T S(T, V ). Für das ideale
Gas erhalten wir mit Gl. (6)
3
F (T, V ) = N kB T − N kB T ln V T 3/2 − T C0
2
(7)
Alternativ kann man die freie Energie durch Integration aus dem totalen Differential
dF = −SdT − pdV
(8)
bestimmen oder die Ergebnisse damit überprüfen.
(b) Analysieren Sie den Carnot-Prozess für ein ideales Boltzmann-Gas. Der CarnotProzess setzt sich zusammen aus einer isothermen Expansion von einem Volumen
V1 zu einem Volumen V2 bei der Temperatur T1 , einer adiabatischen Expansion zu
einer Temperatur T2 < T1 , einer isothermen Kompression bei der Temperatur T2
und einer adiabatischen Kompression zum Ausgangspunkt (T1 ,V1 ). Berechnen Sie
die Arbeit, die vom System in jedem Schritt geleistet wird und die Wärme, die vom
Gas wärend der isothermen Expansion (Kompression) aufgenommen (abgegeben)
wird. Berechnen Sie den Wirkungsgrad (vom System geleistete Arbeit/zugeführte
Wärme) der Carnot-Maschine als Funktion von T1 und T2 .
Wir bezeichnen den Anfangszustand als Zustand 1 (Temperatur T1 , Volumen V1 ).
Nach der isothermen Expansion sei das System in Zustand 2 (Temperatur T1 , Volumen V2 ). Den Zustand nach der adiabatischen Expansion nennen wir Zustand 3
(Temperatur T2 < T1 , Volumen V20 > V2 ), den Zustand nach der isothermen Kompression Zustand 4 (Temperatur T2 , Volumen V10 > V1 ). Wir betrachten jetzt die
einzelnen Prozesse separat:
• 1 → 2: isotherme Expansion
Bei der isothermen Expansion nimmt das Gas die Wärme Q12 auf und verrichtet
die Arbeit W12 (W12 = −∆W , ∆W = geleistete äußere Arbeit)
Z
V2
W12 =
Z
V2
p(V, T1 )dV = N kB T1
V1
V1
V2
dV
= N kB T1 ln ,
V
V1
(9)
wobei wir für den Druck p die Zustandsgleichung des idealen Gases verwendet
haben. Die innere Energie hängt für festes N nicht vom Volumen ab und bleibt
daher konstant. Mit dem ersten Hauptsatz erhalten wir
Q12 = W12 = N kB T1 ln
V2
V1
(10)
• 2 → 3: adiabatische Expansion
Für adiabatische Prozesse gilt per Definition Q23 = 0. Die vom System verrichtete Arbeit entspricht dann dem Betrag der Änderung der inneren Energie:
3
W23 = N kB (T1 − T2 ).
2
(11)
Im weiteren Verlauf der Analyse brauchen wir außerdem das Volumen V20 des
Systems im Zustand 3. Die Entropie bleibt bei adiabatischen Prozessen konstant, mit Gl. (6) gilt deshalb
V T 3/2 = konst
und damit
V20
= V2
T1
T2
(12)
3/2
.
(13)
• 3 → 4: isotherme Kompression
Analog zum Prozess 1 → 2 finden wir
Q34 = W34 = N kB T2 ln
V10
V1
= N kB T2 ln
< 0.
0
V2
V2
Hier haben wir Gl. (13) und die analoge Relation V10 = V1
3/2
T1
T2
(14)
benutzt.
• 4 → 1: adiabatische Kompression
Wie im Prozess 2 → 3 ist Q41 = 0 und W41 = 3N kB (T2 − T1 )/2.
Für den Wirkungsgrad des Carnot-Prozesses erhalten wir
η=
W12 + W23 + W34 + W41
Q12 + Q34
T1 − T2
=
=
.
Q12
Q12
T1
(15)
(c) Berechnen Sie das Integral
I
δQ
,
T
über den Carnot-Prozess für das ideale Boltzmann-Gas. Dabei bezeichnet δQ die
infinitesimale Menge an Wärme die vom System aufgenommen wird und das Integral
läuft über den kompletten Carnot-Prozess. Interpretieren Sie das Ergebnis.
∆S =
Mit den Zwischenergebnisse (10) und (14) finden wir, dass das Integral verschwindet:
I
Q12 Q34
δQ
=
+
= 0.
(16)
∆S =
T
T1
T2
Das Integral muss verschwinden, weil die Entropie eine Zustandgröße ist. Ein von
Null verschiedener Wert dieses Integrals würde bedeuten, dass die Entropie keine
Zustandsgröße sein kann.
(d) Untersuchen Sie den selben Carnot-Prozess in der umgekehrten Richtung (die isotherme Kompression des Gases findet bei der höheren Temperatur T1 statt). Was
ist der Zweck dieses Prozesses? Berechnen Sie die Wärme, die im Prozess aus dem
kalten Wärmebad entnommen wird und vergleichen Sie sie mit der Arbeit, die von
einer externen Maschine geleistet wird um den Prozess zu durchlaufen.
Der inverse Carnot-Prozess kann als Kältemaschine verwendet werden. Der erste
Prozess ist dann die adiabatische Expansion 1 → 4. Im zweiten Prozess 4 → 3,
isotherme Expansion bei Temperatur T2 von V10 nach V20 , nimmt das System Wärme
auf, die dem zu kühlenden Reservoir entzogen wird. Die Wärmemenge kann aus Gl.
(14) abgelesen werden, wir müssen nur die Volumen V1 und V2 vertauschen und
erhalten
V2
Q43 = N kB T2 ln .
(17)
V1
Aus der Betrachtung der inversen Prozesse 1 → 4, 4 → 3, 3 → 2 und 2 → 1 ergibt
sich die Summe der vom System verrichteten Arbeit zu
W = W14 + W43 + W32 + W21 = N kB (T2 − T1 ) log
V2
< 0.
V1
(18)
Die Arbeit muss von einer externen Maschine aufgewendet werden. Für den Wirkungsgrad der Kältemaschine finden wir
η0 =
T2
Q43
=
.
|W |
T1 − T2
2. Ultrarelativistisches Bosegas:
(19)
(10+13+2=25 Punkte, schriftlich)
Die innere Energie U eines ultrarelativistischen Gases von Bosonen, wie zum Beispiel
Photonen, erfüllt U = σV T 4 , wobei σ die Stefan-Boltzmann Konstante und T die Temperatur bezeichnet. Der Druck eines solchen Systems erfüllt p = U/3V wobei V das
Volumen des Systems bezeichnet. Das chemische Potential des ultrarelativistischen Bosegases verschwindet µ = 0. Diese Relationen folgen experimentellen Beobachtungen,
später werden wir sie auch durch eine mikroskopische Theorie fundieren.
(a) Bestimmen Sie die Entropie des Systems S(T, V ) als Funktion von Temperatur und
Volumen indem Sie von der inneren Energie U ausgehen. Berechnen Sie die freie
Energie F (T, V ). Geben Sie die Abhängigkeit des Drucks vom Volumen in einem
adiabatischen Prozess an.
Der Lösungsweg ist ähnlich wie in Aufgabe 1 (a). Für das ultrarelativistische Gas
ist das totale Differential der inneren Energie als Funktion von T und V
dU = σT 4 dV + 4σT 3 dT.
(20)
Wir formen Gl. (2) zu dS = dU/T + pdV /T um und setzen Gl. (20) und p = σT 4 /3
ein. Vergleich mit Gl. (1) liefert
∂S = 4V σT 2 ,
∂T V
∂S 4 3
σT .
=
∂V T
3
(21)
(22)
Die Integration ergibt
4
S = V σT 3 ,
3
(23)
und für die freie Energie
σV T 4
F =−
.
3
(24)
In adiabatischen Prozessen ist S = const. Daraus folgt
V T 3 = const,
V p3/4 = const.
(25)
(26)
In der zweiten Gleichung haben wir wieder p = σT 4 /3 verwendet.
(b) Analysieren Sie einen geschlossenen Carnotzyklus für das ultrarelativistische Bosegas. Berechnen Sie Arbeit, die vom System in jedem Schritt geleistet wird und die
Wärme, die vom System wärend der isothermen Expansion (Kompression) aufgenommen (abgegeben) wird. Bestimmen Sie den Wirkungsgrad (vom System geleistete
Arbeit/zugeführte Wärme) der Carnot-Maschine als Funktion von T1 und T2 .
Wir verwenden die gleiche Notation wie in Aufgabe 1 (b):
• 1 → 2: isotherme Expansion
Mit der Zustandsgleichung p = σT 4 /3 bekommen wir die verrichtete Arbeit
Z
V2
W12 =
p(V, T1 )dV =
V1
σ 4
T (V2 − V1 ).
3 1
(27)
Aus U = σV T 4 erhalten wir direkt die Änderung der inneren Energie. Die
Wärme, die das System aufnimmt, ist dann
4
Q12 = ∆U12 + W12 = σT14 (V2 − V1 ).
3
• 2 → 3: adiabatische Expansion
Adiabatischer Prozess: Q23 = 0. Nach der Expansion ist das Volumen
3
T1
0
.
V2 = V2
T2
(28)
(29)
Mit dem ersten Hauptsatz finden wir die vom System verrichtete Arbeit
W23 = U23 = σ(V2 T14 − V20 T24 ) = σV2 T13 (T1 − T2 )
(30)
• 3 → 4: isotherme Kompression
In Analogie mit Prozess 1 → 2 und mit den Volumenrelationen Gl. (29) und
3
V10 = V1 TT21 folgt
σ 4 0
σ
T2 (V1 − V20 ) = T2 T13 (V1 − V2 ) < 0
3
3
4
3
= σT2 T1 (V1 − V2 ).
3
W34 =
(31)
Q34
(32)
• 4 → 1: adiabatische Kompression
Genauso wie in Prozess 2 → 3 ist Q41 = 0 und W41 = σV1 T13 (T2 − T1 ).
Wir addieren die obigen Zwischenergebnisse und finden für das ultrarelativistische
Gas den Wirkungsgrad
η=
W12 + W23 + W34 + W41
Q12 + Q34
T1 − T2
=
=
.
Q12
Q12
T1
(33)
Das Ergebnis ist identisch zum Wirkungsgrad für den Carnot-Prozess des idealen
Gases, Gl. (15). Der Wirkungsgrad ist universell, er hängt nicht von den Eigenschaften des Gases ab. Man kann das Ergebnis nur aus Entropieüberlegungen mit
dem ersten und zweiten Hauptsatz bekommen (siehe Wikipedia).
(c) Berechnen Sie das Integral
I
δQ
,
T
über den Carnot-Prozess für das ultrarelativistische Bose-Gas. Dabei bezeichnet δQ
die infinitesimale Menge an Wärme die vom System aufgenommen wird und das
Integral läuft über den kompletten Carnot-Prozess. Interpretieren Sie das Ergebnis.
∆S =
Mit den Zwischenergebnissen (28) und (32) erhalten wir
I
Q12 Q34
δQ
=
+
= 0.
∆S =
T
T1
T2
(34)
Auch dieses Ergebnis ist konsistent mit der Tatsache dass die Entropie eine Zustandsgröße ist.
3. Thermodynamische Antwortfunktionen:
(13+12=25 Punkte, mündlich)
Ein magnetisches System sei durch die Zustandsgrößen S, T , Magnetisierung M und
das Magnetfeld H bestimmt. Betrachten Sie die Freie Energie
dF̃ = −SdT − M dH.
Von experimentellem Interesse sind die Antwortfunktionen
∂S ∂S ∂M ∂M cM = T
, cH = T
, χS =
, χT =
.
∂T M
∂T H
∂H S
∂H T
(a) Zeigen Sie:
cH
χT
=
.
cM
χS
Die totalen Differentiale von M (T, H) und S(T, H) sind
∂M dM =
dT + χT dH,
∂T H
cH
∂S dS =
dT +
dH,
T
∂H T
(35)
(36)
Wir lösen Gl. (35) nach dH auf und setzen in Gl. (36) ein und erhalten das totale
Differential von dS aufgefasst als Funktion von T und M :
cH
1 ∂S ∂M 1 ∂S dS =
−
dT +
(37)
dM.
T
χT ∂H T ∂T H
χT ∂H T
∂S Der Vorfaktor von dT auf der rechten Seite ist gerade ∂T = cM /T , wir erhalten
M
also die Relation
T ∂S ∂M cM = cH −
(38)
χT ∂H T ∂T H
Indem wir umgekehrt Gl. (36) nach dT auflösen und in (35) einsetzen erhalten wir
die Beziehung
T ∂S ∂M χS = χT −
(39)
.
cH ∂H T ∂T H
In den Gl. (38) und (39) sind die Ableitungen auf der rechten Seite identisch, wir
können die Kombination von Ableitungen eliminieren. Daraus bekommen wir dann
die gesuchte Beziehung
cM
χS
=
.
cH
χT
(b) Betrachten Sie jetzt das homogene magnetische Material mit
M = χ(T )H.
(40)
Berechnen Sie die Antwortfunktionen cM , cH , χT , und χS und zeigen Sie ausdrücklich dass die obengenannte Relation gilt.
Zunchst berechnen wir cH und cM . Wir verwenden M = χ(T )H in
dF̃ = −SdT − M dH
und integrieren über H:
1
F̃ (T, H) = F̃0 (T ) − χ(T )H 2 .
2
(41)
Damit erhalten wir für die Entropie
S(T, H) = −
∂ F̃
∂T
!
H
1
= S0 (T ) + χ0 (T )H 2 ,
2
(42)
wobei χ0 die Ableitung nach der Temperatur bezeichnet. Aus Gl. (42) können wir
cH berechnen:
∂S
1
cH = T
= c0 (T ) + T H 2 χ00 (T ).
(43)
∂T H
2
Für cM , bei M = konst., schreiben wir die Entropie (42) mit Gl. (40) als Funktion
von M
1
χ0 (T )
S(T, M ) = S0 (T ) + M 2 2
,
2
χ (T )
cM = T
∂S
∂T
M
0
0
χ (T )
1
2
= c0 + T M
2
χ2 (T )
00
1
χ (T )
[χ0 (T )]2
2 2
= c0 + T H χ (T )
−2 3
2
χ2 (T )
χ (T )
0
2
[χ (T )]
.
= cH − T H 2
χ(T )
Die anderen beiden Antwortfunktionen sind
∂M
χT =
= χ(T ),
∂H T
und
χS =
∂M
∂H
(45)
0
(44)
= χ(T ) + Hχ (T )
S
∂T
∂H
.
S
Betrachte nun dS:
dS =
∂S0
1
cH
dT + H 2 χ00 (T )dT + χ0 (T )HdH =
dT + χ0 (T )HdH.
∂T
2
T
Für dS = 0 (S = const)
cH
dT + χ0 (T )HdH = 0
T
Daher
χS = χ(T ) − [χ0 (T )]2
⇒
∂T
∂H
= −χ0 (T )
S
HT
.
cH
H 2T
H 2T
= χT − [χ0 (T )]2
.
cH
cH
(46)
Aus (43), (44), (45), und (46) folgt
cM
[χ0 (T )]2
χS
= 1 − T H2
=
cH
cH χ T
χT
4. Physikalische Bedeutung der Freien Energie:
(25 Punkte, mündlich)
Ein System Σ werde mit einem Wärmereservior R mit Temperatur TR in Kontakt gebracht. Teilchenaustausch sei nicht möglich. Die Volumina beider Systeme seien konstant. Die Änderung der inneren Energie von R kann nur durch Wärmeaustausch erfolgen, dUR = δQR = TR dSR . Das Reservoir R sei so groß, dass TR sich beim Wärmeaustausch praktisch nicht ändert, und somit Zustandsänderungen von R reversibel sind.
Das aus Σ und R bestehende Gesamtsystem sei abgeschlossen. Was bedeutet das für eine infinitesimale Energieänderung der Teilsysteme? Drücken Sie die einzelnen Beiträge
allein durch Änderung der extensiven Variablen UΣ und SΣ aus, und leiten Sie
dUΣ ≤ TR dSΣ
(47)
her. Leiten Sie daraus ein Extremalprinzip für die Helmholtzsche Freie Energie ab.
Das Gesamtsystem ist abgeschlossen, daher ist sicherlich dUtot = 0 und damit, weil sich
Utot aus den Teilsystemen zusammensetzt,
dUR = −dUΣ
(48)
Für den Wärmeaustausch gilt außerdem δQΣ = −δQR .
Wegen dUR = δQR (gegeben) und Gl. (48) können wir δQR durch dUΣ ausdrücken,
δQR = −dUΣ . Mit der Definition dSR = δQR /TR ist die Änderung der Entropie des
Reservoirs
1
dSR = − dUΣ .
(49)
TR
Auch die Entropie setzt sich aus den Teilentropien SR und SΣ zusammen. Wir können
deshalb den zweiten Hauptsatz umformen, um die gesuchte Ungleichung zu erhalten:
0 ≤ dStot = dSΣ + dSR
⇒
dUΣ ≤ TR dSΣ = d(TR SΣ )
Wir betrachten nun zwei Gleichgewichtszustände des Teilsystems Σ, zwischen denen
sich das Teilsystem auf möglicherweise irreversible Weise ändert (z.B. durch Fluktuationen oder durch plötzliche zeitabhängige Prozesse mit einer anschließenden Relaxation ins neue Gleichgewicht). Am Anfang und am Ende eines solchen Prozesses ist das
Teilsystem Σ in einem Zustand mit wohldefinierter Temperatur TΣ = TR . [Bem.: im
Nichtgleichgewicht braucht die Temperatur in Σ nicht wohldefiniert zu sein, obwohl
die Temperatur in R immer wohldefiniert und gleich TR ist.] Es gilt dann für kleine
Änderungen dUΣ von einem Gleichgewicht in ein anderes,
da TΣ = TR
⇒
dUΣ ≤ TΣ dSΣ = d(TΣ SΣ )
Dies ist eine Ungleichung, da der Wärmeaustausch zwischen den beiden Gleichgewichtszuständen irreversibel sein kann. D.h. d(UΣ − TΣ SΣ ) ≤ 0 gilt immer, solange ein System
an ein Wärmebad gekoppelt bleibt.
Das bedeutet aber, dF = dFΣ ≤ 0 (weil dFR = 0). Irreversible Prozesse können also
die freie Energie reduzieren. Das Gleichgewicht ist aber ein Zustand, in dem die thermodynamischen Größen konstant bleiben. Damit diese Bedingung auch für beliebige
irreversible Prozesse erfüllt ist, muss die Helmholtzsche Freie Energie im Gleichgewicht
minimal sein.