1.) Aussagenlogische Ausdrücke und ihre Verknüpfungen

Organisatorische Hinweise:
1.) Teil deiner Aufgabe ist auch, den Inhalt des Worksheets zu verstehen.
2.) Nutze die Hilfe der Betreuer*innen sinnvoll! Insbesondere dann, wenn ein Konzept noch nicht in
einer der Vorlesungen behandelt wurde oder du in Zeitverzug mit der Nachbereitung gerätst.
Viel Spaß!
1.) Aussagenlogische Ausdrücke und ihre Verknüpfungen
Aufbauend auf: Schulwissen
Aufgaben: 8
> restart;
Beispiele von Aussagen und ihren Wahrheitswerten
MATH/MAPLE: Ausgangspunkt der klassischen (zweiwertigen) Aussagenlogik sind Aussagen
mit eindeutig bestimmtem Wahrheitswert "wahr" oder "falsch", d.h., sie sind entweder wahr
oder falsch. In Maple schreiben wir dafür true oder false.
Für uns hat die Aussagenlogik sowohl eine innermathematische Bedeutung bei
1) Formulierungen von mathematischen Sätzen,
2) Beweisen,
3) Beschreibungen von Mengen
als auch eine programmiertechnische Bedeutung bei
1) Abfragen im interaktiven Modus,
2) Abfragen zur Programmsteuerung.
> p:=evalf(Pi,20);
> evalf(42*100/1337)<p;
(1.1.1)
In der letzten Zeile steht eine Aussage. MAPLE kann in diesem Fall entscheiden, ob diese
Aussage wahr (true) oder falsch (false) ist. Dazu verwendet MAPLE das Kommando
evalb ("evaluate boolean", oder auf deutsch "Wahrheitswert auswerten"):
> evalb(%);
true
(1.1.2)
Hierbei bezieht sich % auf das zuletzt berechnete Ergebnis.
Die Aussage "42 ist ein Element der Menge
" oder in Symbolen "
" können wir auch von MAPLE auf den Wahrheitswert auswerten lassen:
> 42 in {23,42,73};
evalb(%);
true
(1.1.3)
Hier sehen wir das Ganze für die Aussage "42 ist eine ganze Zahl" oder "42 ist ein Objekt vom
Typ integer":
> 42::integer;
evalb(%);
true
(1.1.4)
Die Aussage "42 ist eine Primzahl" oder "42 ist vom Typ prime" :
> 42::prime;
evalb(%);
false
(1.1.5)
Einschränkung in der Auswertung von Aussagen in Maple (freiwillig)
Maple kann nur strikte, mathematische Aussagen auswerten. Gewisse Fragen zum Leben, dem
Universum und dem ganzen Rest kann MAPLE nicht sinnvoll auswerten:
> coulditbe(42 = Number_Of_Roads_A_Man_Must_Walk_Down);
true
(1.2.1)
> testeq(x-LambertW(x)=0);
FAIL
(1.2.2)
Wir werden uns in diesem Worksheet auf einfache Aussagen beschränken, welche sowohl wir als
auch MAPLE mathematisch sinnvoll beantworten können.
Zusammensetzung neuer Aussagen durch Verknüpfung
MATH: Unser Augenmerk soll jetzt der Konstruktion neuer Aussagen aus vorgegeben Aussagen
gelten:
- Aussagen können negiert werden durch nicht (Negation), d.h., ist A eine Aussage, so ist auch
"nicht A
A", (ausführlicher: "A gilt nicht") eine Aussage.
- Aussagen können miteinander verknüpft werden. Mathematisch besonders wichtig sind
Verknüpfungen durch und (Konjunktion, ), oder (Disjunktion, ), impliziert (Implikation,
) und äquivalent (Äquivalenz,
).
Sind also A und B Aussagen, so sind auch
"A und B" ("A
B"),
"A oder B" ("A
B"),
"Entweder A oder B",
"A impliziert B" ("A
B", ausführlicher: Wenn A gilt, dann gilt auch B) und
"A ist äquivalent zu B" ("A
B", ausführlicher: A gilt genau dann, wenn B gilt)
Aussagen. Man beachte, dass hier mit oder das nicht ausschließende oder gemeint ist, im
Gegensatz zu entweder oder.
MATH: Aus technischen Gründen nimmt man zu den bisherigen Aussagen noch zwei künstliche
Aussagen hinzu. In der mathematischen Logik bezeichnet man diese beiden Aussagen mit
VERUM (eine immer wahre Aussage) und FALSUM (eine immer falsche Aussage). In Maple
benutzt man dafür ebenfalls true und false. Die Übereinstimmung mit den entsprechenden
Wahrheitswerten ist unproblematisch. Man mache sich nur klar, dass diese Größen hier in einer
Doppelbedeutung (einmal als Aussage und einmal als Wahrheitswert einer Aussage) auftreten.
Wichtigster Punkt: Der Wahrheitswert einer zusammengesetzten Aussage hängt nur von den
Wahrheitswerten der Teilaussagen ab (gemäß der nachfolgenden Tabelle):
A
| Nicht A
-------------------wahr
| falsch
falsch | wahr
A
B
|A und B |A oder B |Entw. A oder B |A impliziert B
---------------------------------------------------------------wahr
wahr
| wahr
| wahr
|
falsch
|
wahr
wahr
falsch | falsch | wahr
|
wahr
|
falsch
falsch wahr
| falsch | wahr
|
wahr
|
wahr
falsch falsch | falsch | falsch |
falsch
|
wahr
Diese Tabellen sind so zu lesen: Ist z.B. die Aussage A wahr und die Aussage B falsch, so ist die
Aussage "A impliziert B" auch falsch.
Anstelle von nicht, und, oder, entweder oder und impliziert schreiben wir in Maple not, and,
or, xor und implies. Man bezeichnet diese Symbole auch als Boolesche Operatoren.
Wir drucken nochmals die Wahrheitstafeln - durch Maple erzeugt - aus und kommentieren dann
die einzelnen Operatoren:
> printf("
a
b |
not a | a and b | a or b | a xor
b |a implies b \n");
printf(" -------------------------------------------------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%7s%7s | %7s | %7s | %7s | %7s | %11s \n",a,b,
not a,a and b,a or b,a xor b,a implies b);
end do
end do;
a
b |
not a | a and b | a or b | a xor b |a implies b
-------------------------------------------------------------------true
true |
false |
true |
true |
false |
true
true false |
false |
false |
true |
true |
false
false
true |
true |
false |
true |
true |
true
false false |
true |
false |
false |
false |
true
MATH: Die Verneinung einer Aussage verändert die Wahrheitswerte, insbesondere hängen die
Wahrheitswerte der verneinten Aussage nur von den Wahrheitswerten der ursprünglichen
Aussage ab und nicht von der Aussage selbst (das bedeutet: es kommt nicht darauf an, welche
Aussage durch a beschrieben wird, es kommt nur auf den Wahrheitswert von a an):
> printf("
a
|
not a \n");
printf("
--------------------\n");
for a in [true,false] do
>
printf(" %8s
end do;
| %8s
\n",a,not a);
a
|
not a
-------------------true |
false
false |
true
DENKANSTOSS
ist anders als in vielen gesprochenen Sprachen, wo eine doppelte Verneinung eine verstärkte
Verneinung ist.)
MATH: Gewisse Aussagen sind immer wahr, zum Beispiel die Aussage "a oder nicht a":
> printf("
a
|
a or not a \n");
printf("
--------------------\n");
for a in [true,false] do
printf(" %8s | %8s \n",a,a or not a);
end do;
a
|
a or not a
-------------------true |
true
false |
true
Man nennt solche Aussagen Tautologien.
Diese Aussage "a oder nicht a" zeigt, dass Maple das sogenannte Law Of Excluded Middle
annimmt. Dieses logische Grundprinzip besagt, dass für eine beliebige Aussage a mindestens die
Aussage a selbst oder ihre Negation not a gelten muss.
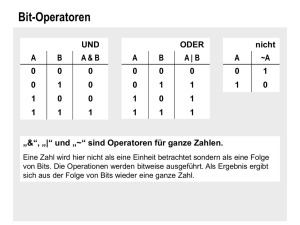
MATH: Die Wahrheitswerte für die und-Vernüpfung liefert folgende Wahrheitstafel, die man
verbal so zusammenfassen kann: "a und b" ist genau dann wahr, wenn sowohl a als auch b wahr
sind. Man beachte, dass unsere Wahrheitstafel jetzt
Zeilen hat, weil alle Kombinationen
der Belegung für a und b berücksichtigt werden müssen.
> printf("
a
b |
a and b \n");
printf(" ----------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %8s \n", a, b, a and b);
end do;
end do;
a
b |
a and b
---------------------------true
true |
true
true
false |
false
false
true |
false
false
false |
false
Wir betrachen ein Beispiel mit einer und-Vernüpfung.
> evalb(1234=7! and 3^3=81);
false
Das Ergebnis lässt uns also schließen (DENKANSTOSS: Warum?), dass eine von drei
Möglichkeiten vorliegt:
1)
und
,
(1.3.1)
2)
und
,
3)
und
.
In der Tat liegt die dritte vor, denn:
> evalb(1234=7!),evalb(3^3=81);
(1.3.2)
MATH: Die beiden Aussagen "a und b" und "b und a" nehmen in der folgenden Wahrheitstafel
immer die selben Werte an. Man spricht von äquivalenten Aussagen.
> printf("
a
b | a and b | b and a\n");
printf(" ---------------------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %8s | %8s \n", a, b, a and b, b and a)
;
end do;
end do;
a
b | a and b | b and a
--------------------------------------true
true |
true |
true
true
false |
false |
false
false
true |
false |
false
false
false |
false |
false
MATH: Man sagt auch, dass die und-Operation kommutativ ist.
MATH: Die Frage, ob zwei (endliche) Aussagen äquivalent sind, ist ein endliches Problem. Das
bedeutet, dass man durch Einsetzen von endlich vielen Kombinationen von Wahrheitswerten die
Äquivalenz von zwei Aussagen entscheiden kann.
Insbesondere kann man mit Hilfe einer Wahrheitstafel beweisen, ob zwei Aussagen äquivalent
sind.
MATH: Die Wahrheitswerte für die oder-Vernüpfung liefern folgende Wahrheitstafel, die man
verbal so zusammenfassen kann: "a oder b" ("a
b") ist genau dann wahr, wenn mindestens
eine der Aussagen a, b wahr ist.
> printf("
a
b |
a or b \n");
printf(" ---------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %8s \n",a,b,a or b);
end do;
end do;
a
b |
a or b
--------------------------true
true |
true
true
false |
true
false
true |
true
false
false |
false
ÜBUNG [01]:
Zeige mit einer Wahrheitstafel in Maple, dass "a oder b" und "b oder a" die selben
Wahrheitswerte liefern.
Hinweis: Die korrekte Benutzung des printf-Befehls sowie das Aussehen der Tabellen sind
hier nebensächlich; es ist also egal, wenn deine Tabellen "schief" sein sollten. Wichtig ist nur
die Korrektheit des Inhalts der Tabelle.
Wir betrachten die folgende Aussage.
> evalb(1234=7! or 3^3=81);
false
Dies lässt nur den Schluss zu, dass sowohl
(1.3.3)
als auch
gilt.
Beispiel:
Wir können jetzt schon die besprochenen Booleschen Operatoren kombinieren und stellen fest,
dass
"nicht(a und nicht b)" sowie
" (nicht a) oder b"
a
b
a b"
dieselben Wahrheitstafeln liefern. Sie sind also äquivalente Aussagen.
> printf("
a
b | not(a and not b) | (not a) or
b\n");
printf(" --------------------------------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %10s
|
%10s
\n",a,b,not(a
and not b),not a or b);
end do;
end do;
a
b | not(a and not b) | (not a) or b
--------------------------------------------------true
true |
true
|
true
true
false |
false
|
false
false
true |
true
|
true
false
false |
true
|
true
MAPLE: Zur Erklärung der Klammerung: not bindet stärker als alle anderen Booleschen
Operatoren, deshalb konnten die Klammern in der letzten Spalte der Tabelle bei der Eingabe
weggelassen werden. and bindet stärker als or. Die genaue Reihenfolge der Ausführung der
logischen Operatoren ist in Maple: not, and, or, xor, implies. Eine Übersicht über die
Bindungsstärke findet man in der HILFE:
?operators,precedence
ÜBUNG [02]:
1.) Zeige mit Maple, dass "not(a or b
a b)" ) und "(not a) and (not b
a
b") äquivalente Aussagen sind.
2.) Zeige mit Maple, dass "not(a and b)" (kurz a b)") und "(not a) or (not b)" (kurz a
b") äquivalente Aussagen sind.
3.) Zeige mit Maple, dass "(not a) implies b" (kurz a
b") und "a or b" (kurz "a b")
äquivalente Aussagen sind.
4.) (freiwillig) Erkläre den Witz im Comic:
MATH: Die ersten beiden Aussagen der letzten Übung haben wichtige Verallgemeinerungen in
der sog. Prädikatenlogik: Die Verneinung der Aussage
"Für alle x: a(x) gilt" (kurz " x: a(x)")
ist
"Es gibt ein x: a(x) gilt nicht" (oder gebräuchlicher in der Umgangssprache "es gibt ein x, so dass
a(x) nicht gilt") (kurz "
wobei a(x) eine von x abhängige Aussage ist.
Falls x nur eine zweielementige Menge durchläuft, wird die erste Aussage zu einer gewöhnlichen
und-Verbindung, während die zweite in diesem Fall zu einer oder-Verbindung der Verneinungen
wird.
Entsprechend ist die Verneinung der Aussage
"Es gibt ein x: a(x) gilt" (kurz " x: a(x)")
die Aussage
"Für alle x: a(x) gilt nicht" (kurz "
.
DENKANSTOSS: Wenn x eine dreielementige Menge, etwa
bedeutet
für alle x: a(x) gilt
dasselbe wie
a(1) und a(2) und a(3).
Was ist bei n-elementigen Mengen? Wie formuliert sich
es existiert ein x: a(x) gilt
in der alten Sprache mit "oder"?
, durchläuft, dann
ÜBUNG [03]:
(Ohne Maple, dafür aber mit Papier und Schreibgerät):
1.) Verneine die Aussage: "Es existiert ein x, so dass für jedes y die Aussage a(x,y) gilt" (kurz "
x: c y: a(x,y)").
2.) Verneine die Aussage: "Für jedes x gibt es ein y, so dass a(x,y) gilt" (kurz " x: y: a(x,y)
").
Schreibe die Verneinung jeweils umgangssprachlich und in Symbolen hin.
Hinweis: Klammern setzen und die Regel aus dem letzten MATH-Abschnitt zweimal
verwenden.
MATH: Die Wahrheitswerte für den Implikations-Operator liefern folgende Wahrheitstafel, die
man verbal so zusammenfassen kann: "a impliziert b" ist genau dann falsch, wenn a wahr und b
falsch ist.
> printf("
a
b | a implies b \n");
printf(" ------------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %11s \n",a,b,a implies b);
end do;
end do;
a
b | a implies b
-----------------------------true
true |
true
true
false |
false
false
true |
true
false
false |
true
Die letzten beiden Zeilen dieser Tabelle geben immer wieder Anlass zu Diskussionen. Aber
irgendwie ist schon klar, dass eine falsche Voraussetzung jeden Schluss richtig macht, nur die
Wahrheit der gefolgerten Aussage kann man nicht erschließen. Für mathematische Beweise sind
die letzten beiden Zeilen dieser Wahrheitstafel oft nicht relevant, denn man schließt in der Regel
so:
Die Aussage a ist wahr, die Implikation "a impliziert b" ist wahr, also ist b wahr.
MATH: Bei einem gewissen Typ von sogenannten Beweis durch Kontraposition zeigt man
"nicht b impliziert nicht a". Letzteres ist äquivalent ist zu "a impliziert b":
> printf("
a
b | a implies b |(not b) implies (not
a)\n");
printf(" -------------------------------------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %11s |
implies b, not b implies not a);
end do;
end do;
%11s \n",a,b,a
a
b | a implies b |(not b) implies (not a)
-------------------------------------------------------true
true |
true |
true
true
false |
false |
false
false
true |
true |
true
false
false |
true |
true
ÜBUNG [04]:
1) Erkläre (kurz!) das Prinzip von Beweis durch Kontraposition.
2) Was hat dieses Beweisprinzip mit der letzten Wahrheitstafel zu tun?
Äquivalenz von Aussagen
MATH: Wir schreiben für die Äquivalenz ein kleines Programm:
> # Dieses Programm erfuellt alle fuer dieses Worksheet
benötigten Zwecke.
# Es is nicht nötig, es neu zu schreiben oder umzuschreiben.
unprotect(equiv);
equiv:=proc(a::boolean,b::boolean)
return (a implies b) and (b implies a)
end proc:
protect(equiv);
Wir überprüfen unser Programm.
> printf("
a
b | a äquivalent b \n");
printf(" ----------------------------------\n");
for a in [true,false] do
for b in [true,false] do
printf("%8s%8s | %14s \n",a,b,equiv(a,b))
end do;
end do;
a
b | a äquivalent b
---------------------------------true
true |
true
true
false |
false
false
true |
false
false
false |
true
equiv(a,b) ist also genau dann wahr, wenn a und b den selben Wahrheitswert haben.
In den folgenden Aufgaben verzichten wir nun auf die Beschreibung der Aussagen in Worten,
sondern beschreiben sie stattdessen ausschließlich in den Symbolen die oben eingeführt wurden.
MATH: Will man die Äquivalenz zweier aussagenlogischer Ausdrücke überprüfen, die von
Aussagen abhängen, so muss man Wertebelegungen testen.
In den obigen Fällen war nur 1 oder 2. Hier ist ein Beipiel mit
:
ÜBUNG [05]:
Zeige die Äquivalenz der beiden Aussagen
"a
(b c)" und "(a
b) (a
c)"
mit Hilfe von Wahrheitstafeln auf zwei Arten: ohne und mit Benutzung der Funktion equiv.
Hinweis: Im ersten Fall (ohne equiv) entsteht eine Tabelle mit 5 Spalten, im zweiten Fall (mit
equiv) eine Tabelle mit 4 Spalten. Denke darüber nach, was der Vorteil der zweiten Tabelle
ist.
ÜBUNG [06]:
1) Führe den folgenden Befehl aus.
> a:='a'; b:='b'; c:='c';
(1.4.1)
2) Überprüfe unter Benutzung der Funktion equiv die Äquivalenz der unten stehenden
Aussagen a)-f). Erzeuge diesmal keine Tabelle, sondern gib nur noch true oder false aus.
(Beachte: mindestens eine der Aussagen ist falsch.)
Hinweis: Denke darüber nach, welche Informationen aus Aufgabe 5 relevant für die Lösung
waren und welche nicht.
3) Mache dir jedesmal die Bedeutung der Ausgabe klar.
a) (Assoziativität von "und") "a (b c)" und "(a b) c"
b) (Assoziativität von "oder") "a (b c)" und "(a b) c";
c) (Distributivität zwischen "und" und "oder") "a (b c)" und "(a b) (a
d) (Distributivität zwischen "oder" und "und") "a (b c)" und "(a b) (a
e) (Charakterisierung der Äquivalenz) "a
b" und "(a b)
a o ¬b)".
f) (Charakterisierung der Äquivalenz) "a
b" und "(a
a) (b
b)".
Hinweis: equiv vergleicht keine allgemeinen Aussagen.
c)"
c)"
3) (freiwillig) Verbessere deine Methode, so dass nicht mehr Aussagen ausgewertet müssen als
notwendig.
Hinweis: Warum wäre es im folgenden Comic denkbar, dass der erste Logiker direkt "No!"
sagt.
Auswertung aussagenlogischer Ausdrücke
MAPLE: Aussagen und deren Verknüpfungen durch Boolesche Operatoren bezeichnen wir hier
allgemein auch als aussagenlogische Ausdrücke. Sind speziell Boolesche Operatoren enthalten,
nennen wir sie auch Boolesche Ausdrücke.
Boolesche Ausdrücke werden von Maple immer sofort ausgewertet, d.h. es werden die
zugehörigen Wahrheitswerte berechnet. Andere aussagenlogische Ausdrücke werden erst durch
das Kommando evalb ausgewertet, soweit Maple dazu in der Lage ist.
HILFE: ?evalb
Ist 1249 eine Primzahl?
> 1249::prime;
evalb(1249::prime);
(1.5.1)
true
(1.5.1)
Der hier notierte Boolesche Ausdruck wird, wie angekündigt, auch ohne evalb sofort
ausgewertet (p wurde oben definiert):
> p<22/7 and x>3;
(1.5.2)
Die Auswertung der speziellen Aussage VERUM bzw. FALSUM (in Maple durch true bzw.
false dargestellt) liefert dabei natürlich true bzw. false.
> evalb(true);
true
(1.5.3)
MAPLE: Es gibt Aussagen, die von Maple (aus welchen Gründen auch immer) nicht
ausgewertet werden können. Daher ist es notwendig, dass in Maple neben true und false
noch eine weitere Ausgabemöglichkeit zur Verfügung steht, nämlich FAIL (weiß ich nicht, auch
maybe genannt). Demzufolge liegt in Maple streng genommen eine dreiwertige Logik zugrunde.
Siehe dazu die Tabellen auf der Hilfeseite von boolean.
HILFE: ?boolean
Weitere Beispiele
> true and false;
false
(1.6.1)
true
(1.6.2)
false
(1.6.3)
false
(1.6.4)
> false implies false;
> not true;
> x:=2:
> x>1 and x<4 and false;
Hier findet keine automatische Auswertung statt:
> x=3;
evalb(x=3);
false
(1.6.5)
ÜBUNG [07]:
Kann aus etwas Falschem etwas Richtiges folgen? Gib ein Beispiel oder einen Gegenbeweis!
ÜBUNG [08]:
Fasse (kurz!) zusammen, warum man mit Hilfe des Computers Beweise von Äquivalenzen von
(endlichen) aussagenlogischen Ausdrücken führen kann.
Hinweis: Gehe insbesondere auf die Endlichkeit der Menge der Wahrheitswerte ein.
DENKANSTOSS: Überprüfe, ob du die Aussagenlogik hinreichend gut verstanden hast, indem
du folgende Aufgabe löst:
Für welche natürlichen Zahlen
gilt die Aussage
?
Hinweis: Teste mit Maple zuerst den Wahrheitsgehalt von
für endlich viele natürliche
Zahlentripel.
2.) Anwendungen: Sätze, Beweise, Algorithmen und
Programme
Aufbauend auf: "Aussagenlogische Ausdrücke und ihre Verknüpfungen"
Aufgaben: 2
> restart;
Sätze und Beweise
MATH: Meistens sind mathematische Sätze Implikationen: Sie haben eine Voraussetzung und
eine Behauptung. Die Anwendung des Satzes sieht meistens so aus:
1) Man verifiziert oder überprüft die Voraussetzung und schließt, dass die Behauptung gilt.
oder (vergl. Diskussion der Implikation)
2) Man falsifiziert die Behauptung und schließt, dass die Voraussetzung auch falsch ist.
Der Beweis eines solchen Satzes geschieht meistens durch eine Kette von (richtigen)
Implikationen ausgehend von der Voraussetzung, bzw. ausgehend davon, dass die
Voraussetzung wahr ist. (Eine andere Möglichkeit des Beweisens wurde schon bei der
Diskussion der Implikation angedeutet: der Beweis durch Kontraposition.)
Relativ wenige Sätze haben keine Voraussetzungen. Z.B. der Satz, den man schon bei Euklid
findet:
MATH: Es gibt unendlich viele Primzahlen. (Eine Primzahl ist eine natürliche Zahl
genau zwei verschiedene Teiler hat: 1 und .)
, die
Einen solchen Satz kann man z.B. durch eine andere Form des Beweises nämlich durch
Kontraposition beweisen: Die Verneinung des Satzes impliziert FALSUM.
Das sieht im vorliegenden Fall wie folgt aus: Angenommen, es gibt nur endlich viele
Primzahlen, sagen wir
. Dann kann man das Produkt dieser Primzahlen bilden:
. Der kleinste Teiler
von
ist auch eine Primzahl, also einer von
. Aber keines dieser teilt
: Alle lassen den Rest 1. Das ist ein Widerspruch.
DENKANSTOSS: Der Beweis kann so umformuliert werden, dass er die schärfere, aber
weniger spektakuläre Aussage beweist:
Ist
die Folge aller Primzahlen, so gilt
.
MAPLE gibt uns ein Gefühl dafür, wie bescheiden diese Aussage ist, wenn wächst:
> Pr:=map(ithprime,[$1..20]);
(2.1.1)
> Pro:=map(k->product(Pr[i], i=1..k)+1,[$1..20]);
(2.1.2)
Trotzdem ist Maple nicht in der Lage, die Aussage allgemein zu beweisen, sondern kann sie
lediglich für einige überprüfen. Übrigens sind die Zahlen aus Pro oftmals keine Primzahlen.
Wir testen das sofort:
> map(isprime, Pro);
(2.1.3)
Algorithmen und Programme
MATH: Ein Algorithmus ist ein Rechenverfahren, welches in endlich vielen Schritten für jeden
Datensatz bestimmter Spezifikation ein wohldefiniertes Resultat liefert. Die Anzahl der
Schritte kann sehr wohl von den Ausgangsdaten abhängen. Ein Programm ist die Umsetzung
eines Algorithmus im Computer, mit deren Hilfe bei Eingabe von Daten das Ergebnis berechnet
wird.
Hier ein Beispiel: Wir wollen
ausrechnen.
Algorithmus:
Ausgangsdaten: eine nichtnegative ganze Zahl
Ergebnisdaten:
Rechenschritte:
Wenn
gilt, dann gib aus.
Ansonsten gib
aus.
Programm = Implementation des Algorithmus:
> FAK:=proc(n::nonnegint)
if n=0 then
return 1;
end if;
return n*FAK(n-1);
end proc:
> FAK(3);
6
(2.2.1)
> seq(FAK(k),k=0..20);
(2.2.2)
Man beachte: Die Anzahl der Schritte ist immer endlich, aber von abhängig.
Ganz wichtig ist die sogenannte Typüberprüfung in der ersten Zeile: Es wird überprüft, ob der
Input/die Eingabe zulässig - also hier eine nichtnegative ganze Zahl - ist. Ohne diese
Typüberprüfung kann man den Computer lahmlegen:
würde nie zu einem Ende
kommen.
> FAK(3/2);
Error, invalid input: FAK expects its 1st argument, n, to be
of type nonnegint, but received 3/2
MAPLE: In dem Programm sehen wir auch eine wichtige Anwendung der Wahrheitswerte auf
die Programmierung: Der Befehl if wertet die dahinter stehende Aussage aus.
DENKANSTOSS: Verstehe das Programm FAK. Lass dir (falls es noch nicht bekannt ist) das
Prinzip der Rekursion erklären. Wer das Prinzip der Rekursion nicht kennt und versteht, wird an
den folgenden Aufgaben sowie am Testat für dieses Worksheet scheitern.
MATH: Wir stellen Folgendes fest: Algorithmen sind vergleichbar mit Sätzen, die konstruktiv,
insbesondere ohne Widerspruchsbeweise, bewiesen sind. Zum Vergleich dient die folgende
Tabelle.
Satz/Beweis
| Algorithmus
|Implementation/Programm
--------------+------------------------+----------------------Voraussetzung | Spezif. d. Eingabedaten|Überprüfung d. Spezif.
Behauptung
| Spezif. d. Ausgabedaten|Ausgabe
Beweisschritte| Rechenschritte
|Programmschritte
Anwendung
|
|Programmlauf
Wir wollen den Zusammenhang von konstruktiv bewiesenem Satz und Algorithmus an dem
Beispiel des ersten Abschnittes einüben:
ÜBUNG [01]:
Verwandle den folgenden Satz in einen Algorithmus:
Voraussetzung: Seien A und B zwei aussagenlogische Formeln in a, b und c.
Behauptung: Wir können in endlich vielen Schritten überprüfen, ob A und B äquivalent sind.
Beweisschritte: Man kann für a, b und c jeweils nur endlich viele (insgesamt acht) Werte
einsetzen. Die beiden Aussagen A und B sind äquivalent genau dann, wenn jede dieser endlich
vielen Einsetzungen für A und B jeweils das selbe Paar an Wahrheitswerten liefert.
Hinweis: Hier ist ausdrücklich keine Implementierung gefordert, sondern ein Text. (Freiwilliger
Zusatz: Gib auch die Implementierung an.)
MAPLE: Entsprechend sollte ein Programm immer kommentiert sein: Ein unkommentiertes
Programm ist wie ein Beweis, zu dem der Satz nicht formuliert ist. In diesem Praktikum haben
wir nur selten Kommentare in den Programmtext geschrieben. Wo immer möglich, ist es deine
Aufgabe, das nachzuholen. Weiter sollte ein Programm immer die Eingabe überprüfen. Das
kann umständlich sein, ist aber wichtig. Neben der Typendeklaration bei der Eingabe kann man
noch if-Abfragen am Anfang des Programmes einbauen. Der Programmablauf endet an den
Stellen, wo return steht. Steht an einer Stelle error, so wird das Programm (und das
Programm, das es aufgerufen hat) abgebrochen und es wird sofort eine Fehlermeldung
ausgegeben.
Das folgende Programm bestimmt die Quersumme einer nicht negativen ganzen Zahl:
> Quer:=proc(n::nonnegint)
if n<10 then
return n;
end if;
return (n mod 10) + Quer(floor(n/10));
end proc:
> 73^42;
irem(73^42,9);
181785870860651639206375228449007889734261427971594700334826599541450986\
3302929
1
(2.2.3)
> Quer(73^42);
irem(%,9);
370
1
(2.2.4)
> Quer(Quer(73^42));
irem(%,9);
10
1
(2.2.5)
> Quer(Quer(Quer(73^42)));
irem(%,9);
1
1
(2.2.6)
ÜBUNG [02]:
1) Verstehe das obige Programm Quer und versieh es mit Kommentaren. (Hinweis: Mache
dich mit dem Programmierprinzip der Rekursion vertraut und analysiere, wie es in Quer
angewendet wird. Das Wort "Ziffer" kann hilfreich sein.)
2) Vergleiche die Reste, die eine nichtnegative ganze Zahl und Quer
bei Division durch 9
lassen.
3) Beweise deine Vermutung aus (2).
4) Erweitere das Programm auf alle ganzen Zahlen (Typ: integer), sodass für
gilt: Quer
Quer .
5) Modifiziere das Programm zu einem neuen Programm AQuer, um die alternierende
Quersumme zu bilden. (AQuer
, d.h. man fängt hinten an).
6) Vergleiche die Reste, die und AQuer
bei Division durch 11 lassen.