Skript Woche 07

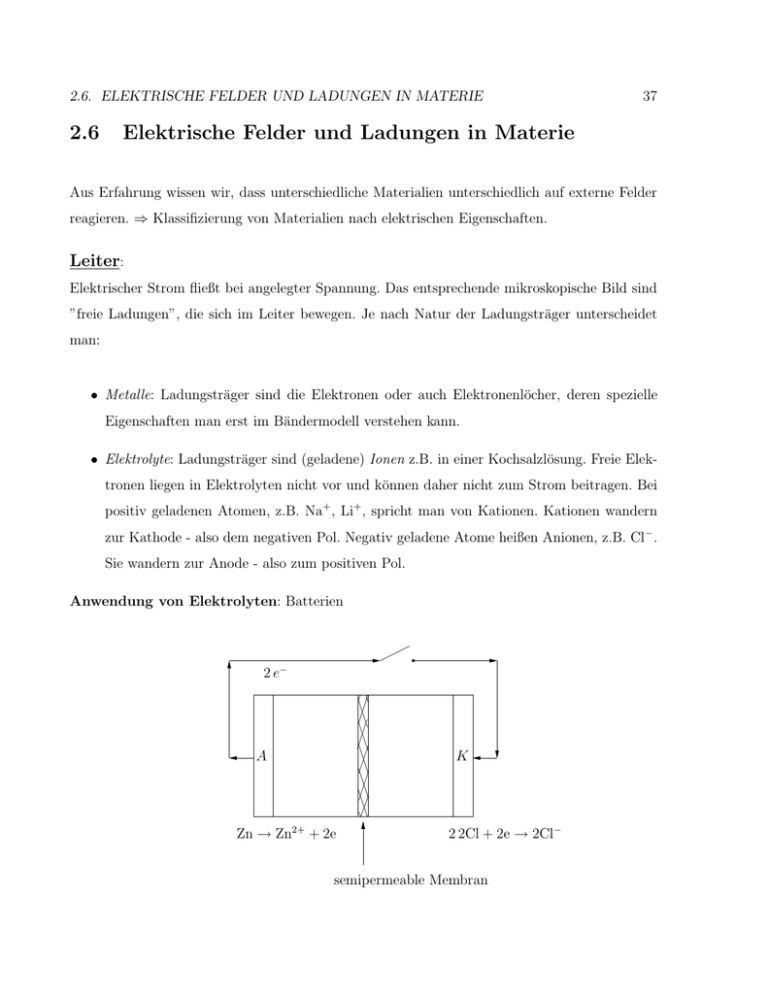
2.6. ELEKTRISCHE FELDER UND LADUNGEN IN MATERIE
2.6
37
Elektrische Felder und Ladungen in Materie
Aus Erfahrung wissen wir, dass unterschiedliche Materialien unterschiedlich auf externe Felder
reagieren. ⇒ Klassifizierung von Materialien nach elektrischen Eigenschaften.
Leiter:
Elektrischer Strom fließt bei angelegter Spannung. Das entsprechende mikroskopische Bild sind
”freie Ladungen”, die sich im Leiter bewegen. Je nach Natur der Ladungsträger unterscheidet
man:
• Metalle: Ladungsträger sind die Elektronen oder auch Elektronenlöcher, deren spezielle
Eigenschaften man erst im Bändermodell verstehen kann.
• Elektrolyte: Ladungsträger sind (geladene) Ionen z.B. in einer Kochsalzlösung. Freie Elektronen liegen in Elektrolyten nicht vor und können daher nicht zum Strom beitragen. Bei
positiv geladenen Atomen, z.B. Na+ , Li+ , spricht man von Kationen. Kationen wandern
zur Kathode - also dem negativen Pol. Negativ geladene Atome heißen Anionen, z.B. Cl− .
Sie wandern zur Anode - also zum positiven Pol.
Anwendung von Elektrolyten: Batterien
PSfrag replacements
+Q
2 e−
−Q
d
A
K
Zn → Zn2+ + 2e
2 2Cl + 2e → 2Cl−
semipermeable Membran
38
KAPITEL 2. ELEKTROSTATIK
Der metallische Draht leitet die Elektronen. Die beiden Zellen werden durch eine semipermeable
Membran voneinander getrennt, die nur Ionen aufgrund ihrer geringen Größe passieren lässt,
jedoch undurchlässig für das Lösungsmittel der Ionen ist. Freie Elektronen gibt es praktisch
nicht im Elektrolyt. K bezeichnet die Kathode in der Abbildung, die ihren Namen trägt, da die
Kationen dorthin wandern. Entsprechend bezeichnet A die Anode. Durch die Elektronen, die
über die externe Leitung kommen, können sich die Cl negativ aufladen und in Lösung gehen.
(Die wirklichen chemischen Reaktionen sind sehr viel komplizierter, aber diese Schritte sind
quasi die Essenz.) Dort lagern sie sich an die positiv geladenen Zink Kationen an. Die Energie,
die durch den Energieübertrag der Elektronen vom Zink an die Chloratome gewonnen werden
kann, ist so nicht einfach verpufft, sondern im Schaltkreis genutzt worden.
Spannung :
Energiegewinn 2 Elektronen
∆U
=
∆Q
2 Elektronen
Beachte: Selbst wenn der Draht ideal leitet, folgt kein unendlich großer Stromfluss, da die
gezeigten Prozesse schließlich nicht unendlich schnell ablaufen können. Diesen Prozessen kann
PSfrag replacements
man genüge
+Q tragen, indem man der Batterie einen inneren Widerstand zuordnet.
−Q
real
ideal
d
Ri
≈
Stromkreis
Stromkreis
permeable Membran
Berechnung von Leitfähigkeiten und Widerstäanden
Ausgangspunkt sind ”freie” Ladungen qn . Auf Ladungen wirken ”Zufallskräfte” (Stöße) deren
summierter Effekt eine Reibungskraft bewirkt. In guter Näherung gilt:
FReibung = −γ · v
(2.38)
2.6. ELEKTRISCHE FELDER UND LADUNGEN IN MATERIE
39
ähnlich wie in Wasser sedimentierende Teilchen.
⇒ Bewegungsgleichung
m·a+γ·v =q·E
Im statischen Grenzfall: a = 0;
(2.39)
E = const
⇒
PSfrag replacements
v=
q
E
γ
(2.40)
+Q
E
−Q
d
dA2
dA1
∆l
∆l
um von der Oberfläche A2 zu A1 zu gelangen. Die
|v|
Anzahl der Ladungen, die durch A1 in dieser Zeit treten (mit der Materialkonstannte ρ als
Eine Ladung benötigt eine Zeit ∆t =
(Zahlen)Dichte der freien Ladungsträger).
Nq = ρ · (A1 · ∆l)
⇒
q · Nq ist die Ladung, die in der Zeit ∆t durch die Fläche A1 treten:
∆Q
q · Nq
q · Nq
=
=
· |v|
(2.41)
∆t
∆l/ |v|
∆l
!"#$
Strom: I
% 2 &
q
A
=
·ρ
·
·
∆l
(2.42)
! "#· E$
γ
∆l
!"#$
! "# $
Spannung: V
Leitfähigkeit: σ geometr. Eigenschaft
!
"#
$
inverser Widerstand: 1/R
⇒ Ohm’sche Gesetz: V = R · I
(2.43)
40
KAPITEL 2. ELEKTROSTATIK
oder wenn das gängige Symbol U für die Spannung verwendet wird:
U =R·I
[R] = 1 Ω =
1C
1V
""
Ohm""
Die Leitfähigkeit ist eine Materialeigenschaft. Symbol: σ.
1 l
·
σ A
1 l
⇒σ =
·
R A
(2.44)
R =
[σ] = 1 S =
1
Ω·m
""
Siemens""
Die inverse Leitfähigkeit heißt spezifischer Widerstand. Sie hat das Symbol ρ aber keine eigene
S.I. Einheit. Werte für Leitfähigkeiten in S (bei Zimmertemperatur)
Material
Leitfähigkeit ·1 S
Klasse
Kohlenwasserstoffe
10−14
Nichtleiter/Isolator
Diamant
10−4
Nichtleiter
2, 5 · 10−4
Nichtleiter
≈ 10−4 ≤ σ ≤≈ 104
Halbleiter
undotiertes Si
dotiertes Si
Tellur
5 · 10−3
Leitungswasser
0, 05
Meerwasser
≈5
Aluminium, Kupfer, Gold
YBa2 Cu3 O7−x
≈ 3, 5 · 107
Elektrolyt
Metalle (σ stark T-abhängig)
≈ 1 bei T = 300 K
(schlechter Leiter)
→ ∞ bei T = 30 K
Supraleiter (keinen elektr. Widerstand)
Wir sehen, dass die Leitfähigkeit - selbst ohne Supraleiter - extrem viele Größenordnungen
abdeckt. Fast alle anderen Eigenschaften der genannten Materialien wie z.B. Dichte oder Elastizitätsmodul, variieren bedeutend weniger. Die große Bandbreite an Leitfähigkeiten kann wieder
über das Bändermodell verstanden werden: Die Anzahl der freien Elektronen kann je nach Ma-
2.6. ELEKTRISCHE FELDER UND LADUNGEN IN MATERIE
41
terial und thermodynamischen Größen wir Druck und Temperatur um viele Dekaden variieren.
Echte Stromspannungscharakteristik der meisten Materialien:
I
I
g replacements
PSfrag replacements
+Q
+Q
−Q
−Q
U
d
U
d
Extremfall
→
Die Unterscheidung “leitet” bzw. “leitet nicht” ist also eher willkürlich. Bei extrem großer Spannung kann es zu einem “Durchschlag” kommen. In Luft macht sich ein Durchschlag durch
einen Blitz bemerkbar. Strom-Spannungs-Charakteristika haben automatisch dann die Eigenschaft I(V ) = −I(−V ), wenn das Material entlang der Richtung des Stromlflusses spiegelsymmetrisch sind - ansonsten kann man (wie Sie später bei der Diode sehen werden) auch einen
PSfrag replacements
nicht-symmetrischen Verlauf haben. Siehe auch die Diskussion in der Besprechung der Aufgabe
+Q
Piezoelektrizität.
−Q
PSfrag replacements
Elektrotechnisches Symbol für einen Widerstand:d
+Q
Serienschaltung:
−Q
d
I
I
R1
=
'
U = U 1 + U2
R2
R1 + R 2
⇒
U = (R1 + R2 ) · I
42
KAPITEL 2. ELEKTROSTATIK
⇒ In Serie geschaltete Widerstände addieren sich.
RSerie = R1 + R2
siehe auch 2.44
(2.45)
PSfrag replacements
⇒ +Q R =
−Q
Parallelschaltung:
d
1 1
· · (d1 + d2 )
σ A
I1
I1 + I 2
I2
I1
I1 + I 2
Iges.
V
U
=
R
%1
&
1
1
=
+
·U
R1 R2
1
=
·U
Rges.
Rparallel =
%
1
1
+
R1 R2
&−1
(2.46)
Fließt durch einen Nichtleiter Ladung hindurch, entsteht dabei Wärme. Diese berechnet sich wie
folgt:
∆U = V · ∆Q
( mit ∆Q = I · ∆t) → = V · I∆t
∆U
⇒ verlorene Energie pro Zeiteinheit (Leistung):
= V · I = R · I 2 = V 2 /R.(2.47)
∆t
Nichtleiter:
Es liegen keine - oder genauer gesagt vernachlässig bar wenige - freie Ladungsträger vor. Ein externes elektrisches Feld bewirkt lediglich eine Polarisierung der Materie, z.B. durch Induzierung
elektrischer Dipole (Verschiebung von Elektronenhülle gegen den Atomkern) oder die Ausrichtung vorher bereits bestehender aber stochastisch verteilter Dipole - wie z.B. in Wasser.
2.6. ELEKTRISCHE FELDER UND LADUNGEN IN MATERIE
43
ohne E-Feld
PSfrag replacements
PSfrag replacements
isotropes Atom/Molekül
+Q
+Q H
mit E-Feld
−Q
−Q
d
O
H
zufällige Orientierung
d
induzierter Dipol
im Mittel ausgerichtet
Die Polarisation berechnet sich in guter Näherung meist zu:
p=α·E
Für zufällig orientierte Dipole ist 'p( = 0, dagegen ist bei im Mittel ausgerichteten Dipolen
'p( = α · E. Hier steht das Symbol '...( für einen Mittelwert, also den Mittelwert über viele Atome und Moleküle. Momentan ist für uns jedoch lediglich relevant: Die Induzierung von
Dipolen/Orientierung von Dipolen bewirkt eine Erhöhung der elektrostatischen Feldenergie
Energiedichte =
1
ε0 εr E2
2
(2.48)
εr ist die Dielektrizitätszahl und stellt eine materialspezifische Größe dar. Man kann nun bereits
ahnen, dass Materialien, in denen die chemischen Bindungen einen starken ionischen Anteil
haben, hohe & Werte haben, weil sich resultierende Dipole nur im externen Feld ausrichten
müssen aber nicht erst induziert werden müssen. Weil Kohlenstoff und Wasserstoff praktisch
dieselbe Elektronegativität haben sind die Partialladungen auf diesen Atomen quasi null. Daher
44
KAPITEL 2. ELEKTROSTATIK
würden wir eine kleine Dielektrizitätskonstante für diese Materialien erwarten. Wassermoleküle
hingegen haben einen großen Dipol, werden also eine große Dielektrizitätskonstante haben. In
SiO2 liegen zwar große Partialladungen vor, aber das Material ist auch sehr steif, weshalb sich
die Ladungen nicht gerne verschieben lassen (zudem ist die Bandlücke sehr groß) und wird daher
keinen extrem großen & Wert haben. Einige Werte sind:
Medium
εr
Vakuum
1
Polymere
≈2
Glas (SiO2 )
≈8
Gummi
≈ 16
Methanol (CH3 OH)
≈ 30
Wasser
≈ 80
Metalle
∞
Verwendung: Dielektrika werden zur Kapazitätssteigerung von Kondensatoren, der Verhinderung elektrostatischer Entladungen oder auch als gate-Material in elektronischen Schaltkreisen
eingesetzt.
Dielektrika haben weitere Klassifizierungen, z.B. gibt es neben den gewöhnlichen Dielektrika:
• Piezoelektrische Materialien: Verformen sich in guter Näherung linear mit einem extern
anliegenden Feld, sodass die relative Längenänderung ∆l/l wie folgt vom externen E-Feld
abhängt:
∆l
=d·E
l
d ist die piezoelektrische Konstante - siehe auch die Zusatzaufgabe diese Woche.
• Ferroelektrika: haben einen permanenten elektrischen Dipol und oft extrem groß Werte für
εr (zum Teil > 1000).