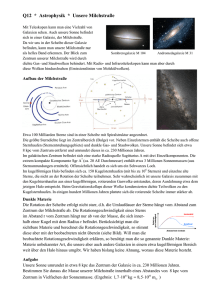
Kosmische und solare Elementhäufigkeiten

Kapitel 3
Kosmische und solare
Elementhäufigkeiten
Das Sonnensystem mit der Sonne, den Planeten und den sonstigen Körpern
ist durch einen gravitativen Kollaps aus dem Material einer galaktischen Molekülwolke im interstellaren Medium entstanden, also aus einer lokalen Verdichtung in dem außerordentlich verdünnten Gas- und Staubgemisch im Raum
zwischen den Sternen. Die Zusammensetzung dieser Wolke, d.h. die Häufigkeit
der 83 stabilen und langlebig radioaktiven chemischen Elemente von H bis Pu
in diesem Material, hat die Häufigkeiten der chemischen Elemente im Sonnensystems festgelegt. Seitdem ist das Sonnensystem in dieser Hinsicht von der
Umgebung praktisch isoliert.
Die Materie in den Sternen und im interstellaren Medium besteht hauptsächlich aus Wasserstoff mit einem Massenanteil von ca. 72% und Helium mit
einem Massenanteil von ca. 26%. Sämtliche anderen Elemente zusammen haben nur einen Massenanteil von ca. 2%. Die Elemente schwerer als H und He
werden vereinfachend pauschal als Metalle“ bezeichnet, obwohl natürlich vie”
le eigentlich keine Metalle im üblichen Sinne sind. Die Sonne besteht, wie alle
anderen Sterne, aus diesem völlig von H und He dominierten Gemisch mit nur
einem sehr geringen Anteil an Metallen. Die großen Gasplaneten Jupiter und
Saturn unseres Sonnensystems enthalten aber bereits einen erheblich höheren
Massenanteil an Metallen und die terrestrischen Planeten schließlich bestehen
fast ausschließlich aus den schwereren Elementen.
Die Zusammensetzung der Materie in der Milchstraße ist nicht überall gleich.
Es werden deutliche, wenngleich auch keine starken, Variationen der Häufigkeiten in Abhängigkeit vom Abstand vom Milchstraßenzentrum beobachtet. Viel
stärkere Variationen werden beobachtet, wenn verschieden alte Sterne untersucht werden. Der Massenanteil Z der Metalle, die sog. Metallizität, nimmt mit
zunehmendem Alter der Objekte ab; es sind sehr alte Sterne mit einer um einen
Faktor bis zu 10−5 mal kleineren Metallhäufigkeit als die der Sonne bekannt.
Die Metalle waren nicht von Anfang an vorhanden, sondern sind erst allmählich
im Verlaufe der 13 Milliarden Jahre seit der Entstehung der Milchstraße aus
den leichten Elementen H und He aufgebaut worden. Am Anfang, gleich nach
dem Urknall, waren praktisch nur H und He vorhanden. Planetensysteme konnten deswegen nicht von Anfang an entstehen, denn zunächst waren die dafür
1
2
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Abbildung 3.1: Prinzipieller Aufbau der Galaxis. Es gibt drei Hauptkomponenten:
Eine dünne Scheibe aus Gas, Staub und metallreichen, jungen Sternen, eine zentrale
Verdickung aus alten und jüngeren Sternen, und einen weit ausgedehnten Halo aus
alten, metallarmen Sternen. Innerhalb des Halos befinden sich das System der Kugelhaufen mit ebenfalls alten, metallarmen Sternen.
erforderlichen Metalle noch nicht vorhanden.
Im Verlaufe der Zeit wurden im Zusammenhang mit den nuklearen Brennprozessen in den Sternen schwere Elemente aufgebaut und durch Massenverlustprozesse an das interstellare Medium abgegeben, aus dem sich später neue
Sterne gebildet haben. Allmählich wuchs die Metallizität der Materie in der
Milchstraße an und hatte vor 4.5 Milliarden Jahren, als unser Sonnensystem
entstand, bereits fast den heutigen Wert erreicht. Ab welchem Wert der Metallizität die Sternentstehung von der Entstehung von Planetensystemen begleitet
wird, ist derzeit nicht genau bekannt.
Die chemische Zusammensetzung des Materials im interstellaren Medium
ist zu einem bestimmten Zeitpunkt in einer bestimmten radialen Entfernung
vom Zentrum der Milchstraße ziemlich homogen. Die Produkte der Elementsynthese in unterschiedlichen Sternen können sehr unterschiedlich sein, aber eine relativ rasche Durchmischung des interstellaren Mediums und des Materials
der Molekülwolken in der Phase vor dem Einsatz von Sternbildung verhindern,
daß große Variationen in der chemischen Zusammensetzung gleich alter Sterne
aus der gleichen Zone in der Milchstraße entstehen. Es gibt so etwas wie eine
universelle kosmische Elementhäufigkeit, in der nur das Massenverhältnis der
Metalle relativ zu H und He stark variiert, während die Häufigkeiten der verschiedenen Metalle relativ zueinander nur geringfügigen Schwankungen unterliegen. Dies bedeutet, daß sich unterschiedliche Planetensysteme hinsichtlich ihrer
chemischen Zusammensetzung nicht sehr wesentlich voneinander unterscheiden
3.1. Aufbau und Entwicklung der Milchstraße
3
können; die Existenz von chemischen Exoten scheint so gut wie ausgeschlossen
zu sein.
Im folgenden wird begründet, warum ein überall ziemlich einheitliches Gemisch schwerer Elemente im interstellaren Medium der Galaxis existiert, und es
wird dargelegt, wie dieses bestimmt wird.
3.1
Aufbau und Entwicklung der Milchstraße
Der großräumige Aufbau unserer eigenen Galaxis kann nur indirekt erschlossen
werden, da wir uns mitten in diesem System befinden. Es wird angenommen,
daß es sich bei unserer eigenen Galaxis um eine normale Spiralgalaxie handelt,
wie sie aus der Beobachtung anderer Galaxien gut bekannt sind. Demnach besteht die Galaxis aus drei Hauptkomponenten: Erstens aus einer ausgedehnten,
dünnen Scheibe, die aus Gas, Staub und vielen – hauptsächlich jungen und
metallreichen Sternen – besteht1 , zweitens im zentralen Bereich aus einem ausgeprägten Wulst, der eine Mischung junger und alter Sterne enthält. Drittens
ist die Galaxis eingebettet in einen ausgedehnten Halo aus sehr alten, metallarmen Sternen, der auch das System der Kugelhaufen enthält, die ebenfalls nur
alte, metallarme Sterne enthalten. In Abb. 3.1 ist schematisch dargestellt, wie
dieses System vermutlich in der Seitenansicht aussieht. Die Sonne befindet sich
in einem Abstand von ca. 8.5 kpc vom Zentrum.
Hier interessieren wir uns insbesondere für die sog. chemische Entwicklung
der galaktischen Scheibe. Darunter versteht man die Entwicklung der Häufigkeit der chemischen Elemente. Probleme, die den zentralen Wulst und den Halo
betreffen, werden nicht betrachtet. Auch wird die feinere Unterteilung der galaktischen Scheibe in eine dünne und eine dicke Scheibe mit jeweils unterschiedlichen Sternpopulationen, die von der Beobachtung nahegelegt wird, nicht weiter
beachtet. Das Modell der chemischen Entwicklung, das hier vorgestellt wird,
enthält ohnehin so viele Vereinfachungen, daß eine detaillierte Beschreibung der
Scheibenstruktur unangemessen wäre.
Zwei Typen theoretischer Modelle wurden bisher für die Entwicklung der
Milchstraße und der Häufigkeiten der chemischen Elemente entwickelt:
ˆ Einfache Einzonenmodelle, in denen die Entwicklung in getrennten, 1 kpc
breiten, zylindrischen Zonen betrachtet wird. Die dynamische Entwicklung der galaktischen Scheibe mit Sternen und ISM wird nicht betrachtet.
Die Entwicklung der Elementhäufigkeiten kann sehr detailliert untersucht
werden
ˆ Chemodynamische Modelle, deren Schwerpunkt auf der dynamischen Entwicklung der Sternpopulation und der Gaskomponente liegt. Die Häufigkeitsentwicklung kann wegen der aufwändigen dynamischen Berechnungen
nur für wenige Elemente (2 oder 3) verfolgt werden
Im folgenden werden nur einfache Einzonenmodelle betrachtet. Eine ausführliche
Beschreibung der Grundlagen für die Konstruktion solcher Modelle findet sich
in Matteucchi [28].
1 Die Scheibe besteht selber aus zwei Komponenten, einer sehr alten, dicken Scheibe, und
einer jüngeren, dünnen Scheibe. Junge Sterne sind nur Bestandteil der dünnen Scheibe, die
aber auch einige sehr alte Sterne enthält
4
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Massen-Einfall
kein radialer
Transport
Abbildung 3.2: Zylindrischer Bereich im Einzonenmodell
3.1.1
Definition der Flächendichten
Zur Berechnung eines Modells der chemischen Entwicklung der galaktischen
Scheibe in der Sonnenumgebung wird diese in zylindrische Ringe einer gewissen
Dicke ∆r unterteilt. Im einfachsten Fall wird angenommen, daß sich die Materie in jedem der Ringe getrennt voneinander entwickelt. Radiale Vermischung
der Materie aus verschiedenen Ringen wird in dieser Näherung vernachlässigt,
obwohl ein radialer Transport in gewissem Umfang tatsächlich stattfindet. Über
die vertikale Verteilung in der Zusammensetzung der Scheibe wird gemittelt
(sog. Einzonennäherung), sodaß in dieser Näherung jeder Ring aus einer homogenen Mischung von Gas und Sternen besteht. Die einzige Variable für jeden
der Ringe ist dann nur die Zeit t.
Die radiale Massenverteilung in der galaktischen Scheibe wird durch die
Flächendichte Σ(r, t) beschrieben. Diese ist als
Σ(r, t) =
Z
+h
dz ρ(r, z, t)
(3.1)
−h
definiert, wobei ρ(r, z, t) die gesamte Massendichte in der Scheibe ist, d.h. sie
umfaßt die Beiträge der Sterne, des interstellaren Gases und des interstellaren
Staubs. h ist die Höhe der Scheibe, gemessen von deren Mittelebene aus.
Die radiale Massenverteilung der interstellaren Materie in der galaktischen
Scheibe wird durch die Flächendichte Σg (r, t) beschrieben. Diese ist entsprechend zu vorher als
Z
+h
Σg (r, t) =
dz ρg (r, z, t)
(3.2)
−h
definiert, wobei ρg (r, z, t) die gesamte Massendichte der interstellaren Materie
ist, also die Summe von Gas- und Staubkomponente. In den einfachen Modellen
wird zwischen Gas und Staub nicht unterschieden und pauschal nur von der
Gaskomponente gesprochen, obwohl ein Teil davon aus interstellarem Staub
besteht. Die Flächendichte der Sterne ergibt sich aus
Σs = Σ − Σg .
(3.3)
Es wird angenommen, daß Materie kontinuierlich auf die galaktische Scheibe einfällt und diese langsam aufbaut, und es wird berücksichtigt, daß unter
Umständen auch ein Ausfluß aus der Scheibe stattfinden kann. Der allmähliche
Aufbau der Scheibe aus einfallendem Material ist ein wesentlicher Bestandteil
3.1. Aufbau und Entwicklung der Milchstraße
5
Tabelle 3.1: Einige wichtige Daten für die Milchstraße in der Sonnenumgebung
Observable
Einheit
beobachtet
Ref.
Gesamte Flächendichte Σ
Flächendichte der ISM Σg
M⊙ pc−2
M⊙ pc−2
50 − 62
7 − 13
13 − 14
30 − 40
2−4
3.5 − 5
0.009 − 0.0326
0.0015 − 0.0109
0.5 − 5
1
2
3
4
5
6
7
7
8
Flächendichte sichtbarer Sterne Σ∗
Flächendichte Sternüberreste
Sternbildungsrate Ψ
SN II Rate RSNII
SN Ia Rate RSNIa
Einfallrate
M⊙ pc−2
M⊙ pc−2
M⊙ pc−2 Ga−1
pc−2 Ga−1
pc−2 Ga−1
M⊙ pc−2 Ga−1
Referenzen: (1) Holmberg & Flynn [19], (2) Dickey [11], (3) Olling & Merrifield [31], (4) Gilmore
et al. [15], (5) Mera et al. [29], (6) Rana [34], (7) Tammann et al. [41], (8) Braun & Thilker [5]
des Modells. Die Diskussion von Modellen, in denen die galaktische Scheibe innerhalb sehr kurzer Zeit durch einen Kollapsprozeß entstanden ist, sodaß die
gesamte Materie in dem betrachteten Ring von Anfang an vorhanden war und
die weitere Entwicklung dann als abgeschlossenes Systems erfolgte, hat gezeigt,
daß solche Modelle mit den beobachteten Eigenschaften des Ensembles von Sternen in der Sonnenumgebung wohl nicht vereinbar sind.
Einige fundamentale Beobachtungsdaten für die Sonnenumgebung in der
Milchstraße sind in Tabelle 3.1 angegeben.
3.1.2
Entwicklung der gesamten Flächendichte
Im folgenden wird angenommen, daß die Scheibe durch einfallende primordiale
Materie aufgebaut wird. Bei kleineren Galaxien als der Milchstraße, bei denen
die Materie nicht so stark gravitativ gebunden ist, spielen auch lokale Ausströmungen aus der Scheibe, angetrieben durch Supernovaaktivitäten, eine Rolle. Die Gleichung für die zeitliche Entwicklung der Flächendichte der galaktischen Scheibe am Ort r lautet
d Σ(r, t)
= Σ̇einf(r, t) − Σ̇wind (r, t) .
dt
(3.4)
Für die Milchstraße wird ein Massenverlust Σ̇wind vernachlässigt, weil eine Beschleunigung der Materie auf die dafür erforderliche hohe Entweichgeschwindigkeit durch die in Frage kommenden Prozesse nicht erreicht werden kann.
Die Einfallrate Σ̇einf(r, t) ist nicht genau bekannt, weder aus theoretischen
Überlegungen, noch aus der Beobachtung. Es wird angenommen, daß in der Anfangsphase der Entstehung der Milchstraße die Massenzufuhr durch Vereinigung
der jungen Milchstraße mit Zwerggalaxien aus dem lokalen Galaxienhaufen dominiert wurde; später dominierte wohl der Einfall von Gaswolken aus dem Medium, in das der lokale Galaxienhaufen eingebettet ist. Es wird zur Vereinfachung
angenommen, daß die Massenzufuhr kontinuierlich in der Zeit erfolgt, obwohl
die Massenzufuhr wohl eher von stochastischer Natur ist. Über die Einzelheiten ist aber nichts sicheres bekannt, weswegen nur eine gemittelte Einfallrate
6
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Tabelle 3.2: Einige Modellparameter für die Berechnung des Aufbaus der galaktischen Scheibe (Dwek [12])
Σ⊙
60 M⊙ pc−2
r⊙
8.5 kpc
Rd
3.5 kpc
tG
12 Ga
betrachtet wird. Für diese macht man folgenden Ansatz
Σ̇einf = A(r) e−t/τ
(3.5)
mit einer empirisch zu bestimmenden Funktion A(r) und einer ebenfalls empirisch zu bestimmenden Zeitkonstanten τ . Dieser spezielle Ansatz bedeutet,
daß die Masseneinfallrate anfangs hoch war und dann relativ schnell abnahm,
daß sich der Masseneinfall aber auch gegenwärtig noch mit einer kleinen, aber
nicht zu vernachlässigenden, Rate fortsetzt. Dieses Verhalten wird auch durch
dynamische Modelle zur Galaxienentstehung nahegelegt.
Integration von Σ̇ über die Zeit vom Zeitpunkt der Entstehung der Galaxis
bis zu einem Zeitpunkt t unter Berücksichtigung der Anfangsbedingung
Σ(r, 0) = 0
und bei Vernachlässigung von Ausströmung ergibt
Σ(r, t) = A(r) 1 − e−t/τ τ .
(3.6)
(3.7)
Sei tG das Alter der galaktischen Scheibe, dann gilt speziell zum heutigen Zeitpunkt
(3.8)
Σ(r, tG ) = A(r) 1 − e−tG /τ τ .
Die Größe A(r) wird dann mit Hilfe der gegenwärtig beobachteten radialen
Verteilung der Flächendichte in der galaktischen Scheibe festgelegt. Ein Ansatz
von der Form
Σ(r, tG ) = Σ⊙ e−(r−r⊙ )/Rd
(3.9)
scheint die radiale Variation der Flächendichte der Scheibe mit ausreichender
Genauigkeit zu beschreiben. Hier ist Σ⊙ die heutige Flächendichte der galaktischen Scheibe in der Sonnenumgebung. Diese wird durch Beobachtungen bestimmt. Die Größe r⊙ ist der mittlere Abstand der Sonne vom galaktischen Zentrum. Die Größe Rd ist ein charakteristischer Längenparameter, der die radiale
Abnahme der gesamten Flächendichte festlegt. Dieser Parameter kann ebenfalls
aus Beobachtungsdaten gewonnen werden. Typische Werte für die Parameter,
die bei Modellrechnungen verwendet werden, sind in Tabelle 3.2 angegeben.
Vergleich mit Gleichung (3.7) zeigt
A(r) =
Σ⊙ e−(r−r⊙ )/Rd
.
1 − e−tG /τ τ
(3.10)
Dadurch ist A(r) für die ganze Scheibe festgelegt. Für die Masseneinfallrate
ergibt sich daraus
Σ⊙ e−(r−r⊙ )/Rd
.
Σ̇einf (r, t) = e−t/τ
(3.11)
1 − e−tG /τ τ
3.1. Aufbau und Entwicklung der Milchstraße
7
80
Σ
Σ [MO· pc-2]
60
40
20
Σg
0
0
5
10
15
t [Ga]
Abbildung 3.3: Zeitliche Entwicklung der gesamten Flächendichte Σ(R⊙ , t) und der
Flächendichte der interstellaren
Materie Σg (r⊙ , t).
Für die charakteristische Zeit τ für den Masseneinfall auf die galaktische
Scheibe wird angenommen, daß diese Zeitskala mit zunehmender Distanz vom
Zentrum zunimmt. Chiappini et al. [9] geben hierfür folgenden Ansatz an
τeinf (r, t) = ar + b .
Wenn eine charakteristische Zeitskala von 4 Ga in der Entfernung r⊙ = 8.5 kpc
vom Zentrum angenommen wird und eine Entwicklungszeitskala von 1 Ga im
Bereich r < 2 kpc des zentralen Wulstes, dann ergibt sich folgender empirischer
Ansatz (Dwek [12])
(
0.4615 r(kpc) + 0.077 Ga für r ≥ 2kpc
τeinf (r, t) =
.
(3.12)
1 Ga
sonst
Dies ist nicht direkt durch Beobachtungen zu belegen; nur der Erfolg der damit
berechneten Modelle rechtfertigt diesen Ansatz.
Mit diesen Annahmen ist die zeitliche Entwicklung der gesamten Flächendichte in der galaktischen Scheibe vollständig festgelegt. Sie ergibt sich aus einer numerischen Lösung der Differentialgleichung (3.4)2 zusammen mit der Anfangsbedingung (3.6). Das Ergebnis für die zeitliche Entwicklung der gesamten
Flächendichte Σ(r⊙ , t) in der Sonnenumgebung mit den in Tabelle 3.2 angegebenen Werten für die Parameter ist in Abb. 3.3 dargestellt.
3.1.3
Entwicklung der Flächendichte der interstellaren Materie
Die Flächendichte der interstellaren Materie Σg (r, t) ändert sich durch folgende
vier Prozesse:
ˆ Die interstellare Materie gewinnt Masse durch einen Einfall von Materie
von außen her mit einer Rate Σ̇einf (r, t). Diese Einfallrate wird durch den
Ansatz (3.11) beschrieben.
2 Mit der hier verwendeten Einfallrate ist die Scheibendichte Σ(r, t) als analytische Funktion
bekannt und Gleichung (3.4) müßte eigentlich nicht numerisch gelöst werden. Bei anderen
Ansätzen für die Einfallrate ist die Lösung aber nicht mehr ohne weiteres als analytische
Lösung zu erhalten
8
Kapitel 3. Kosmische und solare Elementhäufigkeiten
He, Metalle
Massenverlust 6
Urknall
H, He
?
Durchmischung
ISM
Planeten
Sterne
?
Sternbildung
?
WZ, NS, SL
Sternfriedhof
Abbildung 3.4: Kreislauf der Materie im Kosmos zwischen den Sternen und der
interstellaren Materie.
ˆ Die interstellare Materie kann Masse durch Ausströmung aus der galaktischen Scheibe verlieren. Dies wird durch eine Rate Σ̇wind (r, t) beschrieben.
Für ein massereiches System wie die Milchstraße scheint das keine wesentliche Rolle zu spielen; dies ist nur für massearme Systeme von Bedeutung.
ˆ In den dichten Molekülwolken in der interstellaren Materie entstehen ständig neue Sterne aus interstellarer Materie mit einer Rate von Ψ(r, t). Die
interstellare Materie verliert dadurch Masse mit einer Rate −Ψ(r, t).
ˆ Am Ende ihrer Lebensdauer geben die Sterne einen Teil ihrer Masse an
das interstellare Medium zurück. Entweder verlieren sie ein großen Teil ihrer ursprünglichen Masse durch Sternwinde, oder sie erleiden zum Schluß
eine Explosion. Zurück bleibt ein Weißer Zwerg, oder ein Neutronenstern,
oder manchmal ein Schwarzes Loch; in manchen Fällen bleibt auch überhaupt kein Reststern übrig. Die interstellare Materie gewinnt durch diese
Prozesse Masse mit einer Rate R∗ (r, t).
Diese Prozesse bewirken, daß in der Galaxis ein ständiger Kreislauf der Materie zwischen den Sternen und der interstellaren Materie stattfindet. Dieser ist
in Abb. 3.4 schematisch dargestellt. Ein Teil der Materie scheidet aus diesem
Kreislauf in Form der Überreste aus, ein weiterer Teil sammelt sich in der Form
sehr langlebiger, massearmer Sterne an, die seit ihrer Entstehung noch nicht das
Ende ihrer Lebensdauer erreicht haben. Ein Teil der Materie, die auf diese Weise
dem Kreislauf entzogen wird, wird aber von außen durch einfallendes frisches
Material ersetzt, sodaß bisher der Kreislauf noch nicht zum Erliegen kam.
3.1. Aufbau und Entwicklung der Milchstraße
9
Die gesamte Änderung der Flächendichte der interstellaren Materie Σg (r, t)
durch diese Prozesse wird durch folgende Gleichung beschrieben
d Σg (r, t)
= Σ̇einf (r, t) − Σ̇wind (r, t) − Ψ(r, t) + R∗ (r, t) .
dt
(3.13)
Die Rate R∗ (r, t) ist durch die Physik der Massenverlustprozesse der Sterne
bestimmt und die Rate Ψ(r, t) durch die Sternentstehungsprozesse in dichten
interstellaren Wolken. Diese Prozesse werden noch genauer diskutiert. Ein Ausstrom wird im Fall der Milchstraße vernachlässigt. Die Verwendung des gleichen
Ausdrucks (3.11) für die Einfallrate wie in der Gleichung für die gesamte Massendichte unterstellt, daß die Massenzufuhr ausschließlich in Form von Gas und
nicht bereits zum Teil in Form von Sternen, wie beim Einfang von Zwerggalaxien, erfolgt. Eine entsprechende Abänderung der Gleichungen zur Berücksichtigung auch solcher Prozesse bereitet keine Schwierigkeiten; dies wird hier aber
nicht betrachtet und würde auch zu keiner signifikanten Änderung der Ergebnisse führen.
Die beiden Gleichungen (3.4) und (3.13) sind zwei Differentialgleichungen
für die zeitliche Entwicklung der gesamten Flächendichte Σ(r, t) der galaktischen Scheibe und der Flächendichte Σg (r, t) des interstellaren Mediums beim
betrachteten Radius r. Sie müssen mit den Anfangsbedingungen
Σ(r, 0) = 0 ,
Σg (r, 0) = 0
(3.14)
zum Zeitpunkt t = 0 des Beginns des Aufbaus der galaktischen Scheibe gelöst
werden.
3.1.4
Sternentstehung
Der Massenverlust −Ψ(r, t) der interstellaren Materie pro Zeit- und Flächeneinheit ist im Prinzip durch die Sternentstehungsrate Ψ(r, z, M, t) von Sternen der
Masse M pro Volumen- und Zeiteinheit, sowie pro Einheit der Sternmasse, am
Ort r, z zum Zeitpunkt t in der Form
Ψ(r, t) =
Z
h
h
dz
Z
Mo
dM Ψ(r, z, M, t)
(3.15)
Mu
gegeben. Die Massen M der Sterne zum Zeitpunkt ihrer Entstehung variieren
zwischen einer kleinsten Masse Mu = 0.01 M⊙ und einer oberen Massengrenze
Mo = 120 M⊙. Für diese Massengrenzen wird angenommen, daß sie zu allen Zeiten gleich waren; nur für die allererste Sterngeneration gilt dies möglicherweise
nicht. Bei den üblichen Modellen zur chemischen Entwicklung der Milchstraße wird nicht zwischen Einzelsternen und Doppelsternen unterschieden, obwohl
die meisten Sterne Mitglieder in Doppel- oder Mehrfachsternsystemen sind, und
obwohl die Existenz eines Begleiters die Entwicklung eines Sterns gegenüber der
eines Einzelsterns stark verändern kann.
Die Produktionsrate Ψ(r, z, M, t) kann zur Zeit mangels einer begründeten
Theorie der Sternentstehung nicht berechnet werden. Auch kann die Sternbildungsrate nicht direkt den Beobachtungen entnommen werden. Dies ist nur für
die gegenwärtige Sternproduktionsrate in der Sonnenumgebung möglich, aber
nicht für weit zurückliegende Zeiträume. Man nimmt aber an, daß Ψ(r, z, M, t)
10
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Tabelle 3.3: Koeffizienten für den empirischen Ansatz (3.16) für die Sternentstehungsrate
Modell
Theoretisches Modell
Beobachtung
ν
M⊙ /(Ga pc2 )
k
l
0.0117
0.25 ± 0.07
1.5
1.4 ± 0.15
0.5
0
Quelle
(1)
(2)
Quelle: (1) Ballero et al. [3], (2) Kennicutt [24]
proportional zu ρκ ist, wobei ρ die lokale Massendichte der Gaskomponente ist.
Wenn die Sternbildungsrate proportional zur lokalen Gasdichte ist, dann wäre
κ = 1. Wenn die Sternbildungsrate proportional zur Häufigkeit von Stößen zwischen interstellaren Wolken ist, dann wäre κ = 2. Man nimmt allgemein an,
daß vernünftige Werte von κ zwischen beiden Grenzfällen liegen: κ = 1 . . . 2.
Eventuell kann auch die gesamte Flächendichte in der Scheibe auf den Sternbildungsprozeß einen Einfluß haben. Aus diesem Grund wird für die Sternentstehungsrate oft folgender Ansatz gemacht (Chiappini et al. [9])
Ψ(r, t) = ν Σkg (r, t) Σl (r, t) .
(3.16)
Hierin sind ν, k und l Konstanten, die entweder durch Anpassung von Modellen
an bestimmte beobachtete Größen oder aus Beobachtungen der Sterngeburtsrate
in anderen Galaxien festgelegt werden müssen.
Wenn für die Flächendichten als Einheit Sonnenmasse/pc2 verwendet wird
und die Zeit in Einheiten von 1 Ga=109 Jahren gemessen wird, dann können
für die Konstanten die in Tabelle 3.3 angegebenen Werte verwendet werden.
Sterne werden mit einer Verteilung der Anfangsmassen M zwischen einer
unteren Massengrenze Mu und einer oberen Massengrenze Mo geboren. Diese
Verteilung wird mit Φ(M ) bezeichnet. Φ(M )dM beschreibt den Anteil der Sterne mit Massen zwischen M und M + dM , d.h. das Anfangsmassenspektrum3
der Sterne bei deren Entstehung. Diese Funktion ist folgendermaßen normiert
Z Mo
dM Φ(M ) = 1 .
(3.17)
Mu
Die durchschnittliche Masse der Sterne ist
Z Mo
dM Φ(M ) M .
Mm,∗ =
(3.18)
Mu
Nach dem ursprünglichen Vorschlag von Salpeter von 1955, wird diese Massenverteilung durch
Φ(M )dM = CM −µ dM
(3.19)
approximiert. Der Exponent µ kann aus der Häufigkeitsverteilung der Sterne in
der Sonnenumgebung zu µ ≈ 2.35 bestimmt werden. Es wird angenommen, daß
die Anfangsmassenverteilung zu allen Zeiten die gleiche war. Diese Form der
Massenverteilung wird auch heute noch häufig verwendet, wenn es nur auf die
massereichen Sterne ankommt.
3 Englisch:
initial mass function
3.1. Aufbau und Entwicklung der Milchstraße
11
101
100
Φ (M)
10-1
10-2
10-3
10-4
10-5
10-6
10-7
0.01
0.1
1
10
M
100
Abbildung 3.5: Spektrum der Anfangsmassen der Sterne nach Kroupa [25]
Für kleine Sternmassen ist die Salpeter-Verteilung nicht zutreffend. Dann
werden genauere Verteilungsfunktionen verwendet, die ebenfalls aus Zählungen
der Häufigkeiten von Feldsternen oder von Sternen in Sternhaufen abgeleitet
werden. Eine neuere Approximation der Anfangsmassenverteilung wurde von
Kroupa [25] angegeben:
 −0.3

M

C1 M
für Ml ≤ M ≤ M2


l

−1.3



 C2 M
für M2 ≤ M ≤ M3
M2
Φ(M ) =
(3.20)
−2.3

M

für
M
≤
M
≤
M
C

3
4
3
M

3

−2.7



M

C4 M4
für M4 ≤ M ≤ Mu
mit Mu = 0.01 M⊙ , M2 = 0.08 M⊙ , M3 = 0.5 M⊙ , M4 = 1.0 M⊙ , Mo = 120 M⊙ .
Die Konstanten Ci (i = 1 . . . 4) sind so zu bestimmen, daß Φ(M ) an den Intervallgrenzen stetig ist und die Normierung (3.17) erfüllt. Dieses Massenspektrum
ist in Abb. 3.5 dargestellt.
Für die Anfangsmassenverteilung (3.20) beträgt zum Beispiel der Anteil derjenigen Sterne kleiner und mittlerer Masse an den neugeborenen Sternen, deren
Lebensdauer kleiner als das Alter der galaktischen Scheibe ist (das sind die
Sterne mit Anfangsmassen 0.8 < M < 8 M⊙ ) etwa 37.6%, der Massenanteil der
massereichen Sterne (M > 8 M⊙ ) an den neugeborenen Sternen beträgt 6.5%,
und der restliche Anteil von 55.9% sind Sterne mit kleiner bis sehr kleiner Masse (M < 0.8 M⊙ ), deren Lebensdauern größer als das Alter der galaktischen
Scheibe sind. Die mittlere Masse der Sterne ist Mm,∗ = 0.2643 M⊙.
3.1.5
Sternentwicklung
Die Art und Weise, wie sich Sterne entwickeln, hängt stark von ihrer Anfangsmasse M ab. Sterne mit weniger oder mehr als 8 M⊙ Anfangsmasse entwickeln
sich in völlig unterschiedlicher Weise (vergl. Abb. 3.6).
3.1.5.1
Sterne kleiner und mittlerer Masse
Sterne aus dem Massenbereich M <
∼ 8 M⊙ werden als Sterne kleiner und mittlerer Masse bezeichnet. Sie entwickeln sich nach dem Ende des Wasserstoffbrennens
12
Kapitel 3. Kosmische und solare Elementhäufigkeiten
6
He → C+O
C+C→ ... Fe
H → He
5
25 M
4
zum WZ mit 0.85 M
Supernova II
PN-Anregung beginnt
AGB
Zweiter Dredge-Up
zum WZ mit 0.6 M
log L / L
He → C+O
3
5M
H → He
Erster Dredge-Up ↑
thermisches
pulsen
beginnt
Helium
flash
AGB
2
Horizontalast
↑ He → C+O
1
RGB
H → He
↑ Erster Dredge-Up
1M
0
CO-Weisser Zwerg
-1
4.6
4.4
4.2
4.0
3.8
log Teff
3.6
3.4
3.2
Abbildung 3.6: Typische Entwicklungswege von Sternen mit unterschiedlichen An< 2.5 M⊙ , Sterne mittlerer
fangsmassen: Sterne kleiner Masse mit Anfangsmassen M ∼
Masse mit Anfangsmasse zwischen M ≈ 2.5 M⊙ und M ≈ 8 M⊙ , und massereiche
> 8 M⊙
Sterne mit Anfangsmassen M ∼
auf der Hauptreihe zu einem Roten Riesen. Auf dem Roten-Riesenast brennen
sie H in einer Schalenquelle über einem He Kern. Wenn der Kern genügend in
der Masse angewachsen ist, dann zündet das He Brennen und der Stern entwickelt sich vorübergehend zu kleinerer Leuchtkraft und höherer Effektivtemperatur. Bei Sternen mit M >
∼ 2 M⊙ zündet das He-Brennen in einem Kern, in
dem das Elektronengas nicht entartet ist. Die Sterne wandern bereits frühzeitig vom Roten-Riesenast ab und erreichen keine besonders hohe Leuchtkraft
bis zum Zeitpunkt ihrer Abwanderung. Sterne mit M <
∼ 2 M⊙ entwickeln zuerst
einen Kern mit entartetem Elektronengas. Sie müssen sich entlang des RotenRiesenastes sehr weit zu sehr hoher Leuchtkraft und sehr niedriger Effektivtemperatur entwickeln, ehe in ihrem Zentrum die Zündbedingungen für He-Brennen
erreicht werden.
Nach dem Ausbrennen des Zentrums im He-Kern entwickelt sich der Stern
zum zweiten Mal zum Roten-Riesenast (dem Asymptotischen Riesenast, kurz
AGB), wo er He in einer Schalenquelle über einem Kohlenstoffkern (mit etwas
O) brennt. Beim weiteren Anstieg auf dem AGB zündet an der H-He Grenze
erneut das H-Brennen und der Stern geht in eine Entwicklungsphase über, in
der er abwechselnd für einige tausend Jahre H in einer Schalenquelle an der
H-He Grenze und für einige hundert Jahre He in einer Schalenquelle an der HeC-Grenze brennt. Das thermonukleare He-Brennen zündet jeweils impulsartig,
3.1. Aufbau und Entwicklung der Milchstraße
13
sodaß diese Entwicklungsphase als thermisches Pulsen und dieser Teil der AGB
Entwicklung als thermisch pulsender Asymptotischer Riesenast (kurz TP-AGB)
bezeichnet wird.
Während der gesamten Dauer seiner Entwicklung verliert ein Stern Masse
durch einen Sternwind. Der gesamte Massenverlust bis zum Beginn der TP-AGB
Entwicklung ist aber unbedeutend, ausgenommen für Sterne mit Anfangsmassen M <
∼ 1 M⊙ , die auf dem oberen Ende ihrer ersten Entwicklung auf dem
Roten-Riesenast ca. 0.2 M⊙ Masse verlieren. Ursache dessen ist, daß auf dem
oberen Ende des Roten-Riesenastes die Massenverlustrate mit abnehmender Effektivtemperatur und zunehmender Leuchtkraft rasch zunimmt. Beim ersten
Anstieg auf dem Riesenast erreichen nur Sterne mit M <
∼ 1 M⊙ den Bereich
sehr starken Massenverlustes. Beim zweiten Anstieg auf dem Roten-Riesenast
erreichen alle Sterne auf dem TP-AGB den Bereich hinreichend niedriger Effektivtemperatur und hoher Leuchtkraft, in dem die Massenverlustrate dann auf
über 10−5 M⊙ a−1 ansteigt. Die Sterne verlieren dann rasch ihre ganze äußere
Hülle über dem kompakten C+O–Kern und entwickeln sich zu einem Weißen
Zwerg, wobei das thermonukleare Brennen erlischt. Dies beendet ihre Existenz
als Stern; der größte Teil der ursprünglichen Masse ist an das interstellare Medium zurückgegeben worden. Die Entwicklungszeit auf dem TP-AGB ist so kurz
(nur einige 105 Jahre) im Vergleich zu den langen Lebensdauern der Sterne, daß
man zur Vereinfachung annehmen darf, daß die gesamte zurückgegebene Masse
praktisch instantan am Ende der Lebensdauer zurückgegeben wird.
Während der Endphase der Entwicklung der Sterne findet ein Wettlauf zwischen zwei Prozessen statt. Zum einen nimmt die Masse des unverbrannten
Materials im äußeren Bereich des Sterns dadurch ab, daß durch die Brennprozesse im Inneren das noch unverbrannte Material aufgezehrt wird. Zum anderen nimmt die Masse des unverbrannten Materials durch den Massenverlust
im Sternwind ab. Bei Sternen auf dem TP-AGB gewinnt der Sternwind den
Wettlauf und die weitere Entwicklung des Zentralbereichs bricht während des
He-Brennens mangels weiteren Brennmaterials ab.
Die nuklearen Brennprozesse enden bei allen diesen Sternen beim C und O.
Die nuklearen Energiequellen sind damit zwar noch nicht ausgeschöpft, können
aber im Zustand des Weißen Zwergs nicht mehr ausgenutzt werden.
3.1.5.2
Massereiche Sterne
Sterne aus dem Massenbereich M >
∼ 8 M⊙ werden als massereiche Sterne bezeichnet. Sie entwickeln sich nach dem Ende des Wasserstoffbrennens in Richtung zu
einem Roten Riesen. Sie zünden nacheinander alle nuklearen Brennprozesse bis
zum Schluß ein Eisenkern mit entartetem Elektronengas entsteht. Wenn dieser die Chandrasekharsche Grenznasse von 1.4 M⊙ für relativistisch entartetes
Elektronengas überschreitet, dann kollabiert der Kernbereich. Bei Sternen mit
Anfangsmassen kleiner als etwa 40 M⊙ wird der Kollaps beim Erreichen der
Dichte von Kernmaterial gestoppt und es entsteht ein Neutronenstern. Die gewaltige Menge an Gravitationsenergie, die beim Kollaps freigesetzt wird, treibt
den größten Teil des Sternmaterials in einer Explosion als Supernova auseinander. Zurück bleibt ein Neutronenstern mit einer Masse von etwas mehr als
einer Sonnenmasse. Bei sehr massereichen Sternen kann der Kollaps nicht durch
den Aufbau eines Neutronensterns gestoppt werden und der Stern kollabiert in
ein Schwarzes Loch, das wohl den ganzen Reststern verschluckt, sodaß während
14
Kapitel 3. Kosmische und solare Elementhäufigkeiten
1011
Alter der galaktischen Scheibe
108
107
Z=
Z=
0.0
0.
2
00
04
obere Massengrenze AGB
109
untere Massengrenze entwickelter Sterne
Lebensdauer [a]
1010
Entstehung des Sonnensystems
106
1
10
100
M / MO·
Abbildung 3.7: Lebensdauern der Sterne in Abhängigkeit von der Anfangsmasse
M und der Metallizität Z. Zum Vergleich sind das Alter der galaktischen Scheibe
und der Zeitpunkt der Entstehung des Sonnensystems angegeben, sowie die untere
Massengrenze der Sterne, die bis heute das Ende ihrer Lebensdauer erreicht haben
können. (Daten aus Portinari et al. [32])
dieses Vorgangs kein Material abgeworfen wird.
Als Endzustand entsteht bei massereichen Sternen aus dem unteren Massenbereich der massereichen Sterne ein Neutronenstern, aus dem oberen Massenbereich ein schwarzes Loch. Die Grenze zwischen beiden Bereichen ist nicht
genau bekannt; es wird hier ein Wert von 40 M⊙ angenommen, eventuell liegt
die Grenze aber bei nur 25 M⊙ (Fryer et al. [14]).
Auch massereiche Sterne verlieren während ihrer ganzen Entwicklung Masse
durch einen Sternwind. Bei den heißen, massereichen Sternen sind die Massenverlustraten von Anfang an sehr hoch, von der Größenordnung 10−6 . . . 10−5 M⊙ a−1 ,
und der Stern verliert dadurch bereits auf und nahe der Hauptreihe einen nicht
unerheblichen Teil seiner Masse, vor allem bei Anfangsmassen von über 25 M⊙ .
Die nuklearen Brennprozesse laufen aber bei massereichen Sternen so rasch ab,
daß die Brennprozesse den Wettlauf mit den Massenverlustprozessen gewinnen
und noch vor dem Verlust allen unverbrannten Materials durch den Sternwind
alle nuklearen Brennprozesse bis zu den Elementen der Eisengruppe nacheinander ablaufen.
3.1.5.3
Lebensdauern
Die Lebensdauer τ∗ der Sterne muß aus Entwicklungsrechnungen für unterschiedliche Metallizitäten der Sterne bestimmt werden. Die Ergebnisse liegen
in Form von Tabellen vor, aus denen τ∗ (M, Z) durch Interpolation bestimmt
werden kann. Abbildung 3.7 zeigt die generelle Abhängigkeit der Lebensdauern
der Sterne von ihrer Anfangsmasse und ihrer Metallizität.
Die Lebensdauern der massereichen Sterne (M∗ >
∼ 8M⊙ ) sind kurz. Sie variieren zwischen ca. 25 × 106 a an der unteren Massengrenze und etwas über
3.1. Aufbau und Entwicklung der Milchstraße
15
8
7
Mende
6
5
Manfang
4
3
2
MWZ
1
0
1
2
3
4
5
6
7
8
M*
Abbildung 3.8: Die Masse des Weißen Zwergs, der bei Sternen kleiner und mittlerer
Masse zurückbleibt, als Funktion der Anfangsmasse. Die Punkte sind beobachtete Massen Weißer Zwerge in Sternhaufen, bei denen ihre Anfangsmasse auf der Hauptreihe
ermittelt werden kann (Weidemann [46]), die mit Kreuzen markierte Linie die entsprechende empirische Relation zwischen End- und Anfangsmasse. Die Kurve ohne
Markierungen ist das Resultat von Modellrechnungen für die Endmasse als Funktion
der Anfangsmasse für Sterne mit solarer Metallizität. Die mit Manfang gekennzeichnete obere Gerade entspricht der Anfangsmasse der Sterne auf der Hauptreihe. Der
Massenanteil der Sterne kleiner und mittlerer Masse, der an das interstellare Medium
zurückgegeben wird, entspricht der Differenz zwischen der oberen Geraden und der
unteren Kurve für die Masse des Weißen Zwergs
3 × 106 a bei 100 M⊙ . Die Lebensdauern dieser Sterne sind kurz im Vergleich zu
den charakteristischen Zeitskalen für die Entwicklung der galaktischen Scheibe,
die von der Größenordnung 109 a sind, sodaß man mit guter Näherung annehmen dürfte, daß sie denjenigen Teil ihrer Masse, den sie an das interstellare
Medium zurückgeben, praktisch sofort nach ihrer Geburt wieder abgeben, die
sog. instantaneous recycling Näherung. Im allgemeinen wird bei numerischen
Berechnungen von dieser Näherung aber kein Gebrauch gemacht.
Die Lebensdauern der Sterne kleiner und mittlerer Masse sind sehr viel
länger. Bei Sternen mit sehr kleiner Masse übersteigt deren Lebensdauer das
Alter der galaktischen Scheibe. Die Grenze liegt bei etwa 0.8 M⊙ . Alle Sterne
mit kleinerer Masse, die bisher in der Milchstraße entstanden sind, befinden
sich noch immer auf der Hauptreihe. Sie spielen keine Rolle für die chemische
Entwicklung.
Bei den Sternen kleiner und mittlerer Masse spielt die Tatsache, daß ihre
Massenrückgabe erst sehr lange Zeit nach ihrer Entstehung erfolgt, eine ganz
entscheidende Rolle für die Entwicklung der Häufigkeiten derjenigen Elemente,
die ganz oder überwiegend in diesen Sternen synthetisiert werden. Die Produkte
der Nukleosynthese in solchen Sternen erschienen erst nach einer längeren Entwicklungszeit der Galaxis in merklichen Mengen in der interstellaren Materie.
Sie haben in der frühen Phase der Entwicklung der Galaxis noch keine Rolle
gespielt. Speziell gilt das für die Elemente, die ganz oder überwiegend in mas-
16
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Manfang
100
Z = 0.001
Mende
Z = 0.004
10
Z = 0.02
Mrest
Schwarzes Loch ?
NS
1
10
100
M*
Abbildung 3.9: Massenrückgabe an das interstellare Medium durch massereiche
Sterne in Abhängigkeit von der Anfangsmasse. Die oberen gestrichelten Kurven geben
die Masse des Sterns zum Zeitpunkt des Endes des Kohlenstoffbrennens für verschiedene Metallizitäten an (Modelle von Schaller et al. [38]). Die Supernovaexplosion erfolgt
ca. ein Jahr später. Die Massendifferenz zu der mit Manfang gekennzeichneten Geraden wird vom Stern bereits während der Entwicklung auf und nach der Hauptreihe bis
zum Zeitpunkt der Explosion an das ISM abgegeben. Dieses Materie enthält Produkte
des H- und He- Brennens (He, C, N, O). Die unteren gestrichelten Kurven geben die
Restmasse des Sterns nach der Explosion an (nach der Modellrechnung von Woosley &
Weaver [47]). Die Differenz zwischen den oberen Kurven und der angedeuteten Masse
des Neutronensterns wird bei der Supernovaexplosion abgeworfen. Diese Hülle enthält
die Produkte der höheren Brennprozesse (O-, Ne-, Si-Brennen) und in ihr findet hinter
der SN-Stoßwelle weitere Elementsynthese durch explosives Brennen statt. Sterne mit
hoher Anfangsmasse (M > 40 M⊙ ist hier angenommen) kollabieren wahrscheinlich in
ein schwarzes Loch und dieses verschluckt die ganze zum Zeitpunkt des Kollaps’s noch
vorhandene Masse
searmen Sternen synthetisiert werden, die Lebensdauern von vielen Milliarden
Jahren haben.
Ein weiterer wichtiger Aspekt ist, daß in den Sternen kleiner und mittlerer
Masse ein erheblicher Teil der Masse der galaktischen Scheibe gebunden ist.
In der heutigen Milchstraße sind dies über 80% der gesamten Masse. In den
massereichen Sternen ist nur ein kleiner Teil der Gesamtmasse gebunden.
3.1.6
Massenrückgabe
Sterne haben eine endliche Lebensdauer. Am Ende geben sie den größten Teil
ihrer Anfangsmasse an das interstellare Medium zurück:
ˆ Sterne mit Massen M ≤ 8 M⊙ werden zu AGB Sternen, verlieren in einem massiven Sternwind ihre ganze äußere Hülle und lassen einen Weißen
Zwerg mit einer Restmasse von ≈ 0.6 M⊙ zurück. Die Abb. 3.8 gibt einen
Überblick über den zurückgegebenen Massenanteil bei diesen Sternen.
3.1. Aufbau und Entwicklung der Milchstraße
17
ˆ Sterne mit Massen 8 ≤ M ≤ 40 M⊙ explodieren durch Kernkollaps als
Supernova vom Typ II. Zurück bleibt ein Neutronenstern von ≈ 1.5 M⊙ .
Abbildung 3.9 gibt einen Überblick, welcher Teil der Anfangsmasse vor der
Supernovaexplosion schon durch einen Sternwind zurückgegeben wurde
und welcher Teil bei der Explosion abgeworfen wird.
ˆ Sterne mit Massen ≥ 40 M⊙ kollabieren zu Schwarzen Löchern. Diese
geben nur denjenigen Teil der Anfangsmasse zurück, den sie schon vorher
durch einen Sternwind verloren hatten.
Bei der Massenrückgabe werden u.a. auch frisch synthetisierte schwere Elemente
an das ISM abgegeben. Dadurch kommt es zu einer allmählichen Anreicherung
der interstellaren Materie mit schweren Elementen.
Die Rate der Massenrückgabe an das interstellare Medium zum Zeitpunkt t
ist
Mo
Ψ(r, t − τ∗ (M, Z)) Θ(t − τ∗ )
(M − Rrest (M, Z))
Mm,∗
Mu
(3.21)
Hierin ist τ∗ (M, Z) die Lebensdauer eines Sterns der Masse M und der Metallizität Z. Dann ist t − τ∗ (M, Z) der Zeitpunkt, an dem ein Stern einer gegebenen
Masse M und Metallizität Z geboren wurde, der zum Zeitpunkt t das Ende seiner Lebensdauer erreicht hat. Ψ(r, t − τ∗ )/Mm,∗ ist die Gesamtzahl der Sterne,
die zu diesem Zeitpunkt geboren wurden, und dies, mit Φ(M ) dM multipliziert,
liefert die Zahl der Sterne im Massenintervall dM um die Masse M herum. Die
Masse des Sternüberrestes ist Mrest (M, Z) und M − Rrest (M, Z) dementsprechend die zurückgegebene Masse am Ende der Lebensdauer. Die Restmasse wird
den einschlägigen Modellen für die Entwicklung der Sterne entnommen (vergl.
Abbn. 3.8 und 3.9), die auch den Massenverlust durch Sternwinde berechnen
oder den Massenabwurf einer Supernovaexplosion. Diese Massenrückgaberate
wird in Gl. (3.13) für die Entwicklung der Flächendichte der interstellaren Materie verwendet.
Die Integration erfolgt über das Massenspektrum der Sterne, wobei selbstverständlich bei der Berechnung von R∗ nur solche Anfangsmassen M berücksichtigt werden, für die t − τ∗ (M, Z) ≥ 0 ist. Dies wird durch die Heavisidesche
Sprungfunktion Θ gewährleistet. Der Massenbereich, der zu einem Zeitpunkt t
tatsächlich zur Massenrückgabe beiträgt, variiert stark mit t. Während der allerersten Entwicklungsphase tragen praktisch nur massereiche Sterne zur Massenrückgabe bei. Sterne kleiner und mittlerer Masse tragen erst mit einiger
Verzögerung zur Massenrückgabe bei, wobei sich die untere Grenze der Massen, die effektiv zur Massenrückgabe beitragen, mit zunehmendem t zu immer
kleineren Massen verschiebt. Gegenwärtig liegt diese untere Grenze bei 0.8 M⊙ .
R∗ (r, t) =
3.1.7
Z
dM Φ(M )
Modell der Milchstraße
Die gesamte Flächendichte Σ und die Flächendichte Σg der interstellaren Materie sind durch das System der beiden Differentialgleichungen (3.4) und (3.13) zusammen mit der Sternentstehungsrate (3.16) und der Massenrückgaberate (3.21)
bestimmt. Die Flächendichte der Sterne ergibt sich als Differenz Σ∗ = Σ − Σg .
18
Kapitel 3. Kosmische und solare Elementhäufigkeiten
70
60
Holmberg 2004
Σ [MO• pc-2]
50
40
Gilmore 1989
al
tot
30
20
e
rn
ste
10
Dickey 1993
ism
0
0
2
4
6
8
t [Gyr]
10
12
Abbildung 3.10: Zeitliche Entwicklung der gesamten Flächendichte Σtot (durchgezogene Linie), der Flächendichte der sichtbaren Sterne (punktierte Linie), und der
Flächendichte der interstellaren Materie ΣISM (gestrichelte Linie) der galaktischen
Scheibe in der Sonnenentfernung vom galaktischen Zentrum, und der entsprechend
beobachteten Werte für den gegenwärtigen Zeitpunkt (Holmberg & Flynn [19] für
Gesamtdichte, Gilmore et al. [15] für Sterne und Dickey [11] für ISM). Modell von
Zhukovska et al. [48].
Bei Bedarf kann die Flächendichte der Sternreste nach
Z Mo
Ψ(r, t − τ∗ (M, Z)) Θ(t − τ∗ )
d Σrest (r, t)
dM Φ(M )
Rrest (M, Z)
=
dt
Mm,∗
Mu
(3.22)
berechnet werden; auch eine separate Berechnung der unterschiedlichen Arten
von Überresten ist ohne weiteres möglich. Zur Integration der Gleichungen muß
die Entwicklung der Metallizität Z bekannt sein. Diese wird durch eine weitere
Differentialgleichung beschrieben, die erst später angegeben wird.
Typische Ergebnisse von Modellrechnungen für die Entwicklung der Milchstraße in der Sonnenumgebung zeigen die Abbildungen 3.10 und 3.11.
Die Entwicklung der Flächendichten der Sterne und der interstellaren Materie zeigt die Abb. 3.10. Die Ergebnisse der Modellrechnung können mit Beobachtungsdaten für die heutige Flächendichten der Sterne und der interstellaren
Materie in der Sonnenumgebung verglichen werden (Tabelle 3.1). Die Ergebnisse der Modellrechnung stimmen innerhalb der Fehlerbalken mit den beobachteten Werten befriedigend überein. Ähnlich gute Übereinstimmung wird auch für
andere Abstände vom galaktischen Zentrum erzielt. Daten zu anderen als dem
gegenwärtigen Zeitpunkt stehen zum Vergleich naturgemäß nicht zur Verfügung.
Ein anderes interessantes Datum ist die Supernovarate. Diese ist für Supernovae vom Typ II durch
Z Mo
Ψ(r, t − τ∗ (M, Z)) Θ(t − τ∗ )
(3.23)
dM Φ(M )
RSN II =
Mm,∗
MWZ
gegeben. Die Masse MWZ = 8 M⊙ ist die Obergrenze der Anfangsmasse der
Sterne, die sich zu Weißen Zwergen und nicht zu SNe entwickeln. Diese Rate
kann parallel zu einer Modellrechnung bestimmt werden. Die zeitliche Entwicklung der Supernovaraten zeigt die Abb. 3.11. Die Supernovarate ist von Sei-
3.2. Elementsynthese in Sternen
19
Supernova rate, [pc-2Gyr-1]
0.06
0.05
(b)
0.04
0.03
0.02
0.01
0.00
0
2
4
6
8
t [Gyr]
10
12
Abbildung 3.11: Entwicklung der Supernovaraten in der Sonnenumgebung. Die Fehlebalken geben den Bereich der beobachteten Werte an. Modell von Zhukovska et al.
[48].
ten der Beobachtung her leider nur sehr ungenau bekannt. Das Ergebnis einer
Modellrechnung stimmt aber innerhalb der (sehr weiten) Fehlerbalken mit der
Beobachtung überein.
Auch die beobachtete Sternbildungsrate (Tabelle 3.1) kann zum Vergleich
herangezogen werden, aber die Supernovarate ist hierzu proportional; ein Vergleich der Sternbildungsrate liefert also keine unabhängige Information.
Das einfache Einzonenmodell der Entwicklung der Milchstraße ist also in der
Lage, einige grundlegende Eigenschaften der Sonnenumgebung der Milchstraße
gut zu reproduzieren. Das Vergleichsmaterial ist aber leider sehr mager und
die Genauigkeit der Beobachtungsdaten läßt stark zu wünschen übrig, sodaß
eine Beurteilung der Zuverlässigkeit solcher Modelle derzeit kaum möglich ist.
Mangels besserer Alternativen werden sie aber zur Modellierung der chemischen
Entwicklung verwendet, und das, wie wir sehen werden, durchaus mit einigem
Erfolg.
3.2
Elementsynthese in Sternen
Die ursprüngliche Elementmischung im Kosmos nach dem Urknall bestand aus
Wasserstoff, Helium und Spuren von Li. Aus Materie dieser Zusammensetzung
entstanden die ersten Galaxien und die ersten Sterne. Alle schweren Elemente
wurden erst nach und nach durch, oder im Zusammenhang mit, thermonuklearen Brennprozessen in Sternen aufgebaut. Diese Brennprozesse laufen zwar im
Inneren der Sterne bei sehr hohen Drucken und Temperaturen ab, sodaß deren
Produkte nicht unmittelbar in das interstellare Medium gelangen können. Aber
durch Sternexplosionen und durch Mischungsprozesse in Sternen, verbunden
mit Massenverlust durch Sternwinde, können die Produkte der Brennprozesse teilweise oder in Gänze freigesetzt werden. Dies bewirkt eine kontinuierliche
Anreicherung der interstellaren Materie mit den Brennprodukten, die dann bei
der Entstehung neuer Sterne und ihrer Planeten in diese mit eingebaut werden.
Der Gehalt der Sterne an Elementen schwerer als He, die sog. Metallizität Z,
nimmt durch den Kreislauf der Materie zwischen Sternen und der interstella-
20
Kapitel 3. Kosmische und solare Elementhäufigkeiten
ren Materie mit der Zeit beständig zu. Dieser Prozeß wird in den chemischen
Entwicklungsmodellen der Milchstraße (und anderer Galaxien) studiert. Ziel ist
es, die Entwicklung der Häufigkeiten der chemischen Elemente und ihrer Isotopen zu verstehen und möglichst quantitativ richtig durch Modellrechnungen zu
beschreiben.
Ein anderer, empirisch orientierter, Ansatz ist der, für eine möglichst große
Anzahl von Sternen die Häufigkeiten der Elemente aus der Analyse ihrer Spektren zu ermitteln. Dies erlaubt ebenfalls die Auswirkungen der Prozesse der
Elementsynthese zu studieren, indem der Zusammenhang zwischen den Häufigkeiten der einzelnen Elemente und der Metallizität Z studiert wird. Durch den
Vergleich zwischen solchen Daten und Modellrechnungen kann die Aussagekraft
von Modellen getestet werden, um deren Ergebnisse für solche Nuklide verwenden zu können, für die keine Beobachtungsdaten vorliegen.
Beide Methoden sind mit beträchtlichem Erfolg verwendet worden, um den
Bestand der Milchstraße an schweren Elementen und die Prozesse, die dafür
verantwortlich sind, zu verstehen, oft bis hin zu den feineren Details. Die Entwicklung der Häufigkeiten wird in den folgenden beiden Abschnitten behandelt;
in diesem Abschnitt wird kurz die Elementproduktion der Sterne besprochen,
ohne aber auf Einzelheiten der Syntheseprozesse einzugehen (hierzu siehe z.B.
Rohlfs & Rodney [37], Arnett [1]).
3.2.1
Elementsynthese in massereichen Sternen
Sterne mit Anfangsmassen M > 8 M⊙ haben die kürzesten Lebensdauern und
explodieren zum Schluß als Supernovae, wenn ihre Anfangsmasse kleiner als etwa
40 M⊙ war, oder kollabieren anderenfalls zu einem schwarzen Loch. Sie haben
schon seit den frühesten Entwicklungsphasen der Galaxis zur Anreicherung mit
schweren Elementen beigetragen.
Die Massenrückgabe geschieht bei diesen Sternen in zwei Phasen (vergl. Abb.
3.9). Zuerst werden während der Entwicklung auf der Hauptreihe und von dieser weg bis kurz vor dem gravitativen Kollaps des Zentralbereichs durch den
Sternwind die äußeren Schichten des Sterns abgetragen, dann wird entweder bei
der Explosion des Reststerns die verbleibende Masse bis auf die Masse des beim
Kollaps entstehenden Neutronensterns abgeworfen, oder der gesamte Reststern
kollabiert zu einem Schwarzen Loch.
In der ersten Phase entspricht die Häufigkeit der schweren Elemente in der
zurückgegebenen Materie weitgehend den Elementhäufigkeiten in der interstellaren Materie, aus welcher der Stern entstanden ist. Nur einige Nuklide sind in
den Brennprozessen im Stern bis dahin frisch synthetisiert worden. Die massereichen Sterne sind durchweg alle schnelle Rotatoren, bei denen durch die Rotation
Zirkulationsströmungen angefacht werden, die Material aus der Brennzone bis
in die Sternatmosphäre mischen. Vor allem wird dadurch im CN-Zyklus produziertes 14 N an die Oberfläche gebracht und an die interstellare Materie abgegeben; gleichzeitig ist dieses Material an C verarmt, da es in 14 N umgewandelt
wurde. Später werden durch anhaltenden Massenverlust auch direkt Schichten
freigelegt, in denen schon H- und zum Schluß auch He-Brennen stattgefunden
hat, und dadurch deren Produkte an das interstellare Medium abgegeben (He,
N, C, O).
Bei Sternen, die anschließend in ein schwarzes Loch kollabieren (M > 40 M⊙ ),
beschränkt sich der Beitrag zur Produktion schwerer Elemente auf die Produkte
H
101
He
100
Si
S
Mg
N
10
M [MO· ]
Ne
C
-1
Na
-2
10
Ar
Al
Ca
Ni
Cr
P
Cl
-3
10
Mn
Co
K
Ti
F
10-4
10-5
Cu
Zn
V
Sc
Li
10-6
10-7
Z = 0.02
Z = 0.002
Z = 0.0002
Fe
O
3.2. Elementsynthese in Sternen
102
0
B
Be
10
Z
20
30
Abbildung 3.12: Massenrückgabe für die Elemente von H bis Zn bei der Explosion von Supernovae vom Typ II nach den Modellrechnungen von
Woosley & Weaver [47] für drei verschiedene Metallizitäten. Es wurde über eine Kroupa-Anfangsmassenverteilung gemittelt. Für die Elemente,
die direkt durch Brennprozesse aus H oder He aufgebaut werden können, die Primärelemente, hängt die Massenrückgabe wenig oder praktisch
überhaupt nicht von der Anfangsmetallizität ab. Für andere, die nur aus schon vorhandenen schweren Elementen aufgebaut werden können, die
Sekundärelemente, hängt die Massenrückgabe stark von der Anfangsmetallizität ab
21
22
Kapitel 3. Kosmische und solare Elementhäufigkeiten
des H- und He-Brennens, die bis zur Implosion durch den Sternwind abgegeben
wurden.
Bei allen anderen Sternen (M < 40 M⊙ ) wird beim Kollaps des Zentrums
zum Neutronenstern die Resthülle abgeworfen. Diese enthält zusätzlich die Produkte der höheren Brennprozesse jenseits des He-Brennens bis hin zu den Kernen der Eisengruppe, die noch kurz vor der Explosion abgelaufen sind, und
zusätzlich die Produkte der explosiven Brennprozesse, die kurzzeitig angefacht
wurden, als die Supernovastoßwelle durch die Hülle raste. Nur der innere Eisenkern trägt nichts zu den zurückgegebenen schweren Elementen bei, denn dieser
kollabiert ja zum Neutronenstern.
In den Supernovae werden im Prinzip Nuklide aller Element von O bis Bi synthetisiert und zusätzlich die radioaktiven Kerne der Aktiniden. Die Hauptprodukte sind die Elemente von O bis zur Eisengruppe. Die mittlere Massenrückgabe durch massereiche Sterne ist in Abb. 3.12 für unterschiedliche Metallizitäten
dargestellt. Diese enthält auch den Beitrag der bei der Entstehung schon vorhandenen Elemente. Im Durchschnitt ist die Häufigkeit der schweren Elemente
im abgegebenen Material um einen Faktor zehn größer als bei der Entstehung
des Sterns.
Bei den meisten Elementen hängt die Häufigkeit der schweren Nuklide im
zurückgegebenen Material nur wenig von der Metallizität des Sterns ab, da sie
im Prinzip aus H oder He komplett neu synthetisiert werden. Nur bei einigen
Elementen ist eine deutliche Z-Abhängigkeit festzustellen; in diesen Fällen kann
das Element nur aus schon vorhandenen anderen schweren Nukliden mit nennenswerter Ausbeute synthetisiert werden, sodaß die Ausbeute in diesen Fällen
mit steigendem Z zunimmt. Unter den häufigen Elementen sind N und Al zwei
markante Fälle dieser Art. Mit Ausnahme dieser wenigen Fälle ist der Beitrag
der Supernovae zur Anreicherung der Galaxis mit schweren Elementen weitgehend von deren Anfangsmetallizität unabhängig.
In den meisten Modellrechnungen zur chemischen Entwicklung der Galaxis werden zur Zeit Resultate der Modellrechnungen von Woosley & Weaver
[47] verwendet, die für eine Reihe von Anfangsmassen aus dem Bereich 12 bis
40 M⊙ und Metallizitäten zwischen 10−4 und 0.02 die gesamte Massenrückgabe
der massereichen Sterne für die Nuklide der Elemente von H bis Z berechnet
haben. Die publizierten Tabellen enthalten auch den Beitrag der Massenrückgabe durch einen Sternwind vor der Explosion. Bei konkreten Berechnungen wird
die Massenrückgabe der Elemente aus den Tabellen von Woosley & Weaver [47]
durch Interpolation bestimmt. Die in Abb. 3.12 dargestellte Massenrückgabe
für die Elemente von H bis Zn wurde durch Interpolation in diesen Tabellen
für ein genügend dichtes Gitter von Anfangsmassen und Mittelung mit einer
Massenverteilung nach Gl. (3.20) berechnet.
3.2.2
Elementsynthese in Sternen kleiner und mittlerer
Masse
Sterne mit Anfangsmassen M < 8 M⊙ haben lange bis sehr lange Lebensdauern.
Ihr Beitrag zur Anreicherung der Galaxis mit schweren Elementen beginnt mit
beträchtlicher Verzögerung. Erst nach etwa 1 Milliarde Jahre beginnt er den
Beitrag der Supernovae bei denjenigen Elementen zu übertreffen, die sowohl von
massereichen Sterne als auch von deren masseärmeren Verwandten produziert
werden (das sind vor allem C und N).
3.2. Elementsynthese in Sternen
23
10 0
He
-1
10
10-2
O
C
N
X
10-3
Mg
10-4
Al
Na
10-5
27
10-6
Al
26
Al
-7
10
10-8
0
1
2
3
4
5
6
7
8
9
10 11 12 13 14 15
Z
Abbildung 3.13: Massenrückgabe der AGB Sterne für die leichten Elemente, die in
AGB Sternen synthetisiert werden, bei einer Metallizität Z = 0.015. Es wurde über die
Anfangsmassenverteilung Gl. (3.20) über den Massenbereich von 1 bis 8 M⊙ gemittelt.
Die linken Balken geben die Massenanteile des Elements mit der Ordnungszahl Z bei
der Entstehung des Sterns, die rechten Balken den zusätzlichen Massenanteil an frisch
synthetisierten Kernen dieses Elements (die Ausbeute). Bei Al ist der Massenanteil
des radioaktiven Isotops 26 Al separat angegeben
Diese Sterne sind Produzenten von 14 N, das beim Wasserstoffbrennen im
CNO-Zyklus aus C und O erzeugt werden kann, von C (und etwas O) als den
Produkten des He-Brennens, und sie sind die Hauptproduzenten der s-Prozeß
Elemente von Cu bis Bi, die in der He Zone über dem Kohlenstoffkern gebildet
werden, wenn durch (α, n) Reaktionen Neutronen freigesetzt werden, die bevorzugt an den Kernen ab 56 Fe wegen ihrer enorm großen Neutroneneinfangquerschnitte angelagert werden. In gewissem Umfang werden auch einige Nuklide
aus den höheren Zyklen des Wasserstoffbrennens (Ne-Na- und Mg-Al-Zyklus)
in den letzten Entwicklungsstadien erzeugt, wenn die Brenntemperaturen in der
Wasserstoffschalenquelle sehr hoch geworden sind. Während der Entwicklung
auf dem asymptotischen Riesenast werden durch die sog. “dredge-up” Prozesse Produkte der Brennprozesse im Sterninneren bis in die Oberflächenzone der
Sterne gemischt, wodurch diese sich nach einer gewissen Zeit zu Kohlenstoffsternen entwickeln, wenn frisch synthetisierter Kohlenstoff aus dem He-brennen den
vorhandenen Sauerstoff mengenmäßig zu übertreffen beginnt. Die Massenrückgabe mitsamt den frisch synthetisierten Elementen konzentriert sich im wesentlichen auf die kurze Superwindphase auf dem thermisch pulsenden Teil des AGB
am Ende der Lebensdauer der Sterne.
Abbildung 3.13 zeigt die Ausbeute der Elementsynthese für Sterne kleiner
und mittlerer Masse im Bereich der leichten Nuklide. Die Daten wurden den
Tabellen in van den Hoek & Groenewegen [43] entnommen, die zur Zeit mei-
24
Kapitel 3. Kosmische und solare Elementhäufigkeiten
stens bei Modellrechnungen zur chemischen Entwicklung verwendet werden. Die
Daten für Na bis Al stammen aus Karakas & Lattanzio [23].
3.2.3
Elementsynthese in Supernovae vom Typ Ia
Die Supernovae vom Typ II tragen kaum etwas zur Synthese von Elementen
der Eisengruppe im Kosmos bei, weil der Eisenkern kollabiert. Das wenige, was
aus dieser Quelle stammt, wird durch explosives brennen hinter der Supernovastoßwelle erzeugt. Die Hauptlieferanten der Elemente der Eisengruppe sind
Supernovaexplosionen vom Typ Ia, bei denen ein C+O–Weißer Zwerg in einem
Doppelsternsystem explodiert.
Bei Doppelsternsystemen aus einem normalen, noch nicht sehr weit entwickelten Stern und einem Weißen Zwerg, kommt es bei bestimmten Kombinationen des Abstands und des Massenverhältnisses vor, daß ein stabiler Massentransfer vom normalen Stern auf seinen Begleiter, den Weißen Zwerg, stattfindet,
wenn sich der normale Stern im Zuge seiner Entwicklung weg von der Hauptreihe bis zu seiner Rochegrenze (siehe § ??) ausdehnt. Das frische Brennmaterial,
das dadurch auf der Oberfläche des Weißen Zwergs deponiert wird, kann entweder intermittierend zünden und in Novaexplosionen wieder abgeworfen werden,
was zu keiner Massenerhöhung des Weißen Zwergs führt, oder es kann in einem Teil der Fälle kontinuierlich brennen und die Brennprodukte dem Weißen
Zwerg hinzufügen. Wenn dessen Masse die Chandrasekharsche Grenzmasse von
1.4 M⊙ nahezu erreicht, zündet das C-brennen in der entarteten Materie explosiv und es läuft die ganze Sequenz der Brennprozesse bis zum Fe ab. Es kommt
zur Detonation, und weil die Fusion des Ausgangsmaterials (C und O) zum Fe
noch genügend nukleare Energie freisetzt, wird das gesamte Material auf mehr
als Entweichgeschwindigkeit beschleunigt. Es bleibt kein Reststern zurück. Die
freigesetzte Materie besteht ausschließlich aus schweren Kernen von C bis Ni,
wobei die Elemente der Fe-Gruppe den Hauptanteil stellen. Jede einzelne Explosion einer Supernova vom Typ Ia führt dem interstellaren Medium fast 1 M⊙
Fe, Ni und die anderen Elemente der Eisengruppe zu.
Die Abbildung 3.14 zeigt, welche Elemente in welchen Mengen durch die Detonation eines C+O–Weißen Zwergs freigesetzt werden. Die Daten sind Iwamoto et al. [21] entnommen. Der Abbildung ist zu entnehmen, daß auch merkliche
Mengen an C, O, Si und S abgegeben werden, aber dieser Beitrag zur Synthese dieser Elemente ist weitaus geringer als die Beiträge der Supernovae und der
AGB-Sterne und spielt deswegen keine nennenswerte Rolle für die Anreicherung
von C, O, Si und S in der Galaxis.
3.3
3.3.1
Chemische Entwicklung der Milchstraße
Entwicklung der Elementhäufigkeiten
Die Häufigkeiten der Elemente beschreibt man im Rahmen der einfachen Einzonenmodelle am besten durch die Flächendichten Σg,i (r, t) der Elemente i im
interstellaren Medium. Diese beschreiben die Masse des Elements i pro Flächeneinheit (üblicherweise 1 pc2 ) zum Zeitpunkt t in der Entfernung r vom galaktischen Zentrum. Bei Bedarf können entsprechend auch die einzelnen Isotope
der Elemente separat betrachtet werden. Es wird nicht unterschieden, ob sich
100
Fe
Z = 0.02
Z=0
C
-1
10
S
Ni
Ar
Mg
-2
Ca
Cr
Ne
10
M [MO· ]
Si
O
Mn
Co
Al
10-3
P
10-4
K
Na
10-5
Ti
Cl
Zn
V
Cu
N
10-6
3.3. Chemische Entwicklung der Milchstraße
101
Sc
-7
10
10-8
0
10
Z
20
30
Abbildung 3.14: Massenrückgabe für die Elemente von C bis Zn bei der Explosion eines C+O–Weißen Zwergs beim Erreichen der Chandrasekharschen Grenzmasse als Supernova vom Typ Ia (Modellrechnung von Iwamoto et al. [21]). Diese Supernovae sind die Hauptlieferanten für Fe und die
sonstigen Eisengruppenelemente
25
26
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Tabelle 3.4: Häufigkeit der Elemente (Massenanteil) nach dem Urknall (Coc et
al. [10])
Isotop
ǫ
2
3
H
−5
2.6 × 10
4
He
−5
1.04 × 10
He
0.248
7
Li
4.15 × 10−10
die Elemente in der Gasphase oder im interstellaren Staub befinden. Es gilt
offensichtlich
X
Σg,i .
(3.24)
Σg =
i
Der Massenanteil eines Elements i an der interstellaren Materie ist
Xi =
Σg,i
Σg
und die Metallizität Z der interstellaren Materie ist
X
Xi .
Z=
(3.25)
(3.26)
i
Elemente schwerer
als He
Die Häufigkeit der Elemente ǫi relativ zu Wasserstoff läßt sich durch die Flächendichten wie folgt ausdrücken
ǫi =
Σg,i AH
,
Σg,H Ai
(3.27)
wobei AH und Ai die Atomgewichte des Wasserstoffs und des Elements i sind.
Die Entwicklung der chemischen Häufigkeiten wird durch Gleichungen analog zur Gleichung für die Flächendichte der interstellaren Materie beschrieben:
d Σg,i (r, t)
dt
+
Z
Mo
Mu
dM Φ(M )
= X0,i Σ̇einf (r, t) − Xi Σ̇wind (r, t) − Xi Ψ(r, t)
Ψ(r, t − τ∗ (M, Z)) Θ(t − τ∗ )
(M − Rrest (M, Z)) Xi,∗ . (3.28)
Mm,∗
Hier ist Xi der Massenanteil des Elements i in der interstellaren Materie, Xi,∗
der Massenanteil an der zurückgegebenen Materie und X0,i der Massenanteil an
der von außen einfallenden Materie. Es ist angenommen, daß bei der Sternentstehung alle Elemente entsprechend ihrer Häufigkeit in der interstellaren Materie
in die neu entstehenden Sterne eingebaut werden.
Diese Gleichungen müssen zusammen mit den Gleichungen für die Entwicklung der Flächendichten Σ und Σg gelöst werden, in die die Metallizität Z
eingeht. Die Anfangsbedingungen sind
Σg,i (r, 0) = 0 .
(3.29)
Zur Berechnung von Z ist es aber nicht erforderlich, die Gleichungen (3.28)
wirklich für alle Elemente zu lösen. Durch Addition der Gleichungen für alle
Elemente schwerer als He ergibt sich nämlich eine Gleichung für die Flächendichte der schweren Elemente, aus der Z bestimmt werden kann. Es reicht dann,
3.3. Chemische Entwicklung der Milchstraße
27
1
log (Z), [Fe / H]
[Fe / H]
0
-1
log(Z)
-2
-3
-4
0
2
4
6
8
10
12
t [Gyr]
Abbildung 3.15: Entwicklung der Metallizität Z des ISMs in der Entfernung der
Sonne r⊙ vom galaktischen Zentrum und das [Fe/H] Häufigkeitsverhältnis (Zhukovska et al. [48]). Die Fehlerbalken zeigen die beobachtete Alters-Metallizität Beziehung
nach Rocha-Pinto [36]. Die dünne vertikale Linie deutet den Geburtszeitpunkt des
Sonnensystems an und die beiden gefüllten Kreise die beobachteten Metallizitäten der
Sonne und des heutigen interstellaren Mediums
diese Gleichung zu lösen und zusätzlich die Gleichungen (3.28) für diejenigen
Elemente, für die man sich speziell interessiert.
Die Massenteile X0,i müssen entsprechend den Annahmen festgelegt werden,
wie die Zusammensetzung der einfallenden Materie aussieht. Für die Standardannahme, daß es sich um Materie mit der Zusammensetzung gleich nach dem
Urknall handelt, sind die Massenanteile in Tabelle 3.4 angegeben.
Die Massenanteile Xi,∗ (M, Z) der Elemente in der zurückgegebenen Materie
am Ende der Lebensdauer von Sternen mit der Anfangsmasse M und Anfangsmetallizität Z muß Modellrechnungen für die Sternentwicklung entnommen werden. Dafür stehen die weiter oben angegebenen Tabellen zur Verfügung.
3.3.2
Modellrechnungen
Als Beispiel der Ergebnisse von Modellrechnungen zur Entwicklung der Milchstraße in der Sonnenumgebung zeigt Abb. 3.15 die Entwicklung der Metallizität
Z des interstellaren Mediums in der Sonnenumgebung vom Beginn der Entstehung der galaktischen Scheibe bis zum heutigen Zeitpunkt. Zum Vergleich mit
Beobachtungen stehen zum einen die beobachtete Metallizität junger Sterne,
die gerade aus dem interstellaren Medium gebildet wurden, zum anderen die
Metallizität der Sonne zum Zeitpunkt von vor 4.57 Ga zur Verfügung. Modellrechnungen zur chemischen Entwicklung stimmen mit den beiden beobachteten
Werten gut überein, wie der Abb. zu entnehmen ist.
Die Abbildung zeigt ferner den Zusammenhang zwischen der Metallizität Z
und der Eisenhäufigkeit [Fe/H]. Die Größe [X/H] wird für beliebiges Element X
als
[X/H] = log ǫX − log ǫX,⊙
(3.30)
definiert. Hier ist ǫX die Häufigkeit des Elements X relativ zu Wasserstoff (nach
Teilchenzahl) und ǫX,⊙ der entsprechende Wert in der solaren Elementmischung.
Insbesondere ist [X/H] = 0, wenn das Element die gleiche Häufigkeit wie in der
28
Kapitel 3. Kosmische und solare Elementhäufigkeiten
[El/Fe]
1.0
C
O
Mg
Si
S
Ca
0.0
-1.0
[El/Fe]
1.0
0.0
-1.0
-3
-2
-1
[Fe/H]
0
-3
-2
-1
[Fe/H]
0
-3
-2
-1
[Fe/H]
0
Abbildung 3.16: Entwicklung der Elementhäufigkeiten der häufigen Elemente (Kurven) in numerischen Modellen (Zhukovska et al. [48]) für die Entwicklung der Sonnenumgebung in der Milchstraße und Vergleich mit beobachteten Häufigkeiten in F und
G Sternen in der Sonnenumgebung (diverse Punkte). Durchgezogene Linien: Produktionsraten der schweren Elemente durch SN II nach Nomoto et al. [30]. Gestrichelte
Linien: Produktionsraten der schweren Elemente durch SN II nach Woosley & Weaver
[47]. (Quellen der Beobachtungsdaten siehe Abb.3.18)
Sonne hat. Diese Größe wird gerne bei der Diskussion der chemischen Entwicklung verwendet, weil sie die Abweichungen der Häufigkeit eines Elements von der
Elementhäufigkeit in der Sonne augenfälliger erkennen läßt als die Verwendung
der Häufigkeit ǫX selber.
Die Häufigkeit [Fe/H] spielt bei allen derartigen Diskussionen eine besondere
Rolle aus folgendem Grund: Da Eisen hauptsächlich in Supernovae vom Typ Ia
produziert wird, läuft die Produktion von Fe in der Milchstraße wegen der langen
Lebensdauer der Vorläufersterne nur langsam an. Deswegen kann die Häufigkeit
von Eisen in der interstellaren Materie als Maß dafür verwendet werden, wieviel Zeit seit der Entstehung der galaktischen Scheibe vergangen ist. Das setzt
natürlich voraus, daß die Sternentstehung in der Milchstraße über die ganze
Zeit hinweg kontinuierlich verlaufen ist, also weder zeitweilig unterbrochen wurde, noch Phasen plötzlich stark erhöhter Sternbildungsraten aufgetreten sind.
Dies scheint für die Milchstraße zuzutreffen, aber von anderen Galaxien weiß
man aus Beobachtungen, daß die Annahme einer kontinuierlichen Entwicklung
keineswegs bei allen Galaxien zutreffend ist.
Die Größe [Fe/H] kann aus der Analyse des Sternspektrums relativ einfach
abgeleitet werden, während das Alter eines Sterns nur dann einigermaßen zuverlässig festgestellt werden kann, wenn er Mitglied eines Sternhaufens ist. Deswegen wird [Fe/H] als ein Ersatz für den Zeitpunkt der Entstehung eines Sterns
verwendet, auch wenn der Zusammenhang zwischen [Fe/H] und Entstehungs-
3.4. Kosmische Elementhäufigkeiten
29
zeitpunkt nicht genau bekannt ist. Abbildung 3.15 zeigt den empirischen ermittelten Zusammenhang zwischen [Fe/H] und dem Entstehungszeitpunkt der
Sterne, für die aus dem Spektrum ein Wert für [Fe/H] bestimmt wurde. Die Ungenauigkeiten dieser Methode der Festlegung des ungefähren Alters eines Sterns
sind sehr groß, aber genauere Informationen sind derzeit nicht erhältlich. Der
aus Modellrechnungen zur chemischen Entwicklung bestimmte Zusammenhang
zwischen Entstehungszeitpunkt und [Fe/H] stimmt leidlich gut mit dem beobachteten Zusammenhang überein, aber Abweichungen bei kleinen Metallizitäten
sind unübersehbar. Die Diskrepanzen sind aber wahrscheinlich eher eine Folge
der geringen Genauigkeit der Altersbestimmung von Sternen als ein Anzeichen
für ein Versagen der Modellrechnung.
Eigentlich wäre die Metallizität Z ein geeigneteres Maß für den Entstehungszeitpunkt eines Sterns, aber die Bestimmung der Metallizität setzt voraus, daß
für einen Stern die Häufigkeiten aller Elemente bestimmt werden, die wesentlich
zur Metallizität beitragen. Das ist aufwendig und nicht immer möglich, deswegen
die Bevorzugung von [Fe/H] als leichter zu bestimmende Größe. Die Modellrechnungen zeigen, daß sich Z und [Fe/H] in gleichförmiger Weise entwickeln, sodaß
auch [Fe/H] ein geeigneter Indikator für den Entstehungszeitpunkt ist.
Die Abb. 3.16 zeigt die Ergebnisse einer Modellrechnung für die Entwicklung
der Elementhäufigkeiten für einige Elemente, die für die Bildung von terrestrischen Planeten wichtig sind. Die Linien zeigen die Ergebnisse, die man bei der
Verwendung zweier verschiedener Tabellen für die Häufigkeiten der Elemente in
den Massenauswürfen von Supernovae vom Typ II erhält. Bei den mit gestrichelten Linien dargestellten Ergebnissen wurden die Daten der älteren Modellrechnung für Elementsynthese in SN II von Woosley & Weaver [47] verwendet. Die
durchgezogenen Kurven entsprechen einem Entwicklungsmodell, bei dem neuere
Daten für SN II von Nomoto et al. [30] verwendet wurden; letztere scheinen die
Beobachtungsdaten besser zu reproduzieren.
3.4
Kosmische Elementhäufigkeiten
Die Informationen über die Häufigkeit der 83 stabilen oder langlebig radioaktiven Elemente im Kosmos stammen aus folgenden Quellen:
ˆ Analyse der Spektrallinien in der Sonnenatmosphäre. Das liefert brauchbare Informationen über die Häufigkeit von etwa 60 Elementen. Für die
restlichen Elemente kann die Häufigkeit in der Sonne nicht bestimmt werden wegen entweder zu geringer Häufigkeit oder weil keine verwertbaren
Linien vorhanden sind.
ˆ Analyse der Spektrallinien heller, also naher Sterne, für die hochaufgelöste
Spektren gewonnen werden können. Meistens sind nur für ca. 10 ... 20
Elemente Häufigkeiten bestimmbar, weil naturgemäß keine ebenso hoch
aufgelöste Spektren wie für die Sonne gewonnen werden können.
ˆ Laboranalyse der Häufigkeiten schwerflüchtiger Elemente in CI Meteoriten. Dies liefert für ebenfalls ca. 60 Elemente genaue Werte der Häufigkeiten, aber das sind nicht die gleichen 60 Elemente, deren Häufigkeit aus
dem Sonnenspektrum bestimmt werden kann. Unter anderem erhält man
Häufigkeitsinformationen für die meisten der Elemente, deren Häufigkeit
in der Sonnenatmosphäre nicht festgestellt werden kann.
30
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Die kosmische Häufigkeit der Elemente wird im wesentlichen aus diesen drei
Informationsquellen bestimmt.
3.4.1
Häufigkeiten in Sternen und in der Sonne
Die Elementhäufigkeit in der Sonne und in Sternen wird aus dem Spektrum
durch Bestimmung der Fläche der Einsenkung einer Spektrallinie eines Atoms
eines Elements gegenüber der kontinuierlichen Emission des Sterns bestimmt.
Das setzt voraus, daß isolierte Linien im Spektrum gefunden werden können,
die nicht von ähnlichen starken Linien der Atome anderer Elemente überlagert
werden. Wegen der großen Zahl von Linien im Spektrum eines Sterns ist das
für die meisten Linien nicht erfüllt. Für die meisten Elementen lassen sich nur
einige wenige geeignete Linien finden. Für Elemente mit kleiner Häufigkeit ist
es oft nicht möglich, überhaupt irgendwelche geeigneten Linien zu finden, da
sie von den zahlreichen schwachen der Linien der häufigen Elemente überlagert
werden. Deswegen kann die Häufigkeit einiger Elemente nicht aus dem Spektrum der Sonne bestimmt werden. Auch die Bestimmung der Häufigkeiten der
Edelgase aus dem Sonnenspekrum ist, außer für He, nicht möglich, weil deren
Energiezustände über dem Grundzustand energetisch zu hoch liegen und in der
Sonne praktisch nicht angeregt werden können4 .
Insgesamt können bei der Sonne für etwa 60 Elemente deren Häufigkeiten aus
der Analyse der Spektrallinien mit ausreichender Genauigkeit bestimmt werden.
Bei anderen Sternen ist die Situation naturgemäß ungünstiger, da wegen
der geringen verfügbaren Lichtmenge die erreichbare Wellenlängenauflösung begrenzt ist. Das Problem der Überlagerung mit anderen Linien tritt dort verstärkt
auf und verhindert meistens, daß für mehr als ca. 20 der relativ häufigen Elemente deren Häufigkeit bestimmt werden können.
Zur Analyse der Elementhäufigkeiten in anderen Sternen werden fast ausschließlich Sterne der Spektralklassen F und G verwendet. Kühlere Sterne (Klassen K, M) haben zahlreiche Molekülbanden im Spektrum, wodurch sich das
Problem der Überlagerung von Linien drastisch verschärft. Heiße Sterne (Klassen O, B) sind rasche Rotatoren. Zum einen werden die Linien dann durch
den Dopplereffekt stark verbreitert, was sie meist für eine Analyse unbrauchbar macht. Zum anderen werden durch rasche Rotation langsame Zirkulationsströmungen im Stern angeregt, die Material aus den nuklearen Brennzonen bis
an die Oberfläche bringen. Dadurch sind deren Häufigkeiten nicht immer die
Originalhäufigkeiten, mit denen der Stern entstanden ist. Das liefert zwar interessante Informationen über die Sternentwicklung, macht diese Sterne aber
wenig geeignet zur Bestimmung der kosmischen Elementhäufigkeiten.
F und G Sterne bereiten die geringsten Schwierigkeiten bei der Analyse
der Spektren und, solange sie noch nicht das erste Riesenstadium erreicht haben, gibt es keine störenden Durchmischungsprozesse. Sterne vom Spektraltyp
später G Sterne habe außerdem derart lange Lebensdauern, daß alle jemals in
der Milchstraße entstandenen Sterne dieser Typen die Hauptreihe noch nicht
verlassen haben. Man kann deswegen sehr alte Sterne mit außerordentlich kleiner Metallhäufigkeit finden, die schon zu Beginn der Entstehung der Milchstraße
gebildet wurden. Das ermöglicht es, die Entwicklung der Häufigkeiten zu untersuchen.
4 Das gilt im Grundsatz natürlich auch für He, aber wegen dessen großer Häufigkeit sind
trotz schwacher Anregung die Linien gerade noch ausreichend stark für eine Analyse
31
1
1
0
0
-1
-1
[O/H]
[C / H]
3.4. Kosmische Elementhäufigkeiten
-2
-3
-2
-3
-4
-4
-4
-3
-2
-1
0
1
-4
-3
-1
0
1
0
1
[Fe/H]
1
1
0
0
-1
-1
[Si/H]
[Mg / H]
[Fe / H]
-2
-2
-3
-2
-3
-4
-4
-4
-3
-2
-1
[Fe / H]
0
1
-4
-3
-2
-1
[Fe/H]
Abbildung 3.17: Kohlenstoff-, Sauerstoff-, Magnesium– und Siliziumhäufigkeit in G
Sternen in der Sonnenumgebung der Milchstraße in Abhängigkeit von der Eisenhäufigkeit (Quellen der Daten siehe Abb.3.18). Dies demonstriert die allmähliche Zunahme
der Elementhäufigkeiten in der Milchstraße durch die Prozesse der Elementsynthese in
Sternen und der Massenrückgabe an das interstellare Medium durch Supernova Explosionen vom Typ Ia und Typ II. Ein Häufigkeitsverhältnis von [Fe/H]= −1 entspricht
etwa einem Alter von 109 Jahren
Abbildung 3.17 zeigt die Ergebnisse der Häufigkeitsbestimmungen von C, O,
Mg und Si in G Sternen aus der Sonnenumgebung. Die Elemente O, Mg und
Si werden fast ausschließlich in Supernovaexplosionen vom Typ II gebildet und
wurden bereits in der allerersten Phase der Entstehung der Milchstraße synthetisiert und gleich der interstellaren Materie beigemischt. Kohlenstoff wird ebenfalls in Supernovaexplosionen synthetisiert, der Hauptteil des C in der Milchstraße wird aber von AGB-Sternen produziert, deren Produktion wesentlich später
einsetzt. Dies ist für den Knick“ im Anstieg von [C/H] verantwortlich, der sich
”
bei [Fe/H]≈ −1 andeutet.
Es ist ein ganz klarer Entwicklungseffekt erkennbar: Die Häufigkeit der Elemente war Anfangs sehr niedrig und hat durch die Prozesse der Elementsynthese
in Sternen und durch den Materiezyklus in der Galaxis kontinuierlich zugenommen. Zum Zeitpunkt der Entstehung des Sonnensystems war die Häufigkeit
dieser Elemente etwa halb so hoch wie die der jüngsten Sterne (größtes [Fe/H])
in der hier dargestellten Stichprobe, die erst innerhalb der letzten ca. 1 Ga
Kapitel 3. Kosmische und solare Elementhäufigkeiten
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
[N/Fe]
[C/Fe]
32
0
-0.2
0
-0.2
-0.4
-0.4
-0.6
-0.6
-0.8
-0.8
-2
-1.5
-1
-0.5
0
-2
-1.5
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0
-0.2
-0.4
-0.5
0
-0.5
0
-0.5
0
-0.5
0
0.2
0
-0.2
-0.8
-2
-1.5
-1
-0.5
0
-2
-1.5
[Fe/H]
-1
[Fe/H]
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
[Si/Fe]
[Al/Fe]
0
-0.6
-0.8
0
-0.2
-0.4
0
-0.2
-0.4
-0.6
-0.6
-0.8
-0.8
-2
-1.5
-1
-0.5
0
-2
-1.5
[Fe/H]
-1
[Fe/H]
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
[Ca/Fe]
[S/Fe]
-0.5
-0.4
-0.6
0
-0.2
-0.4
0
-0.2
-0.4
-0.6
-0.6
-0.8
-0.8
-2
-1.5
-1
-0.5
0
-2
-1.5
[Fe/H]
-1
[Fe/H]
0.8
0.8
0.6
0.6
0.4
0.4
0.2
0.2
[Ni/Fe]
[Ti/Fe]
-1
[Fe/H]
[Mg/Fe]
[O/Fe]
[Fe/H]
0
-0.2
0
-0.2
-0.4
-0.4
-0.6
-0.6
-0.8
-0.8
-2
-1.5
-1
[Fe/H]
-0.5
0
-2
-1.5
-1
[Fe/H]
Abbildung 3.18: Entwicklung der Häufigkeiten von C, N, und O und der wesentlichen staubbildenden Elemente mit der Metallizität für F und G Sterne in der Sonnenumgebung. Daten aus Gratton & Sneden [16] (für Al), Magain [27] (für Al), Edvardsson et al. [13], Chen et al. [8], Reddy et al. [35], Gratton et al. [17] (für O, Si), Venn
et al. [44] (für Mg, Ca, Ti, Ni), Soubiran [39] (für O, Al, Si), Caffau et al. [6] (für S),
Jonsell et al. [22] (für O, Al, Si), Israelian et al. [20] (für N)
3.4. Kosmische Elementhäufigkeiten
33
entstanden sind und die Häufigkeiten im heutigen interstellaren Medium repräsentieren. Die ältesten Sterne in der Stichprobe sind mindestens 10 Ga alt
und haben erst ca. 1/1000 der Metallhäufigkeit der Sonne. Es sind auch Sterne
mit noch geringerer Häufigkeit gefunden worden, die aber in der Stichprobe in
Abb. 3.17 nicht enthalten sind.
Die Abbildung zeigt, daß die Häufigkeiten der Sterne bei ihrer Entstehung
zu einem bestimmten Zeitpunkt von Stern zu Stern nur gering variiert. Die
Streuung des Meßdaten in der Abbildung ist praktisch gleich der Ungenauigkeit
bei der Bestimmung der Elementhäufigkeiten aus Sternspektren. Die Variation
der Häufigkeiten in der interstellaren Materie, aus der Sterne entstehen, scheint
für einen bestimmten Zeitpunkt tatsächlich nur sehr gering zu sein, wie es in
den Modellrechnungen zur chemischen Entwicklung immer angenommen wird.
In der Abb. 3.18 sind die Resultate einiger Studien zur Entwicklung der
Elementhäufigkeiten für eine Auswahl von Elementen dargestellt, die für die
Gesteinsbildung und die Bildung des Eisenkerns von Planeten von Bedeutung
sind. Hier sind die Häufigkeiten [X/Fe] relativ zur Fe-Häufigkeit dargestellt.
Diese Darstellung läßt manche Entwicklungseffekte deutlicher Erkennen als eine
Darstellung wie in Abb. 3.17.
Die Häufigkeiten von Kohlenstoff und Stickstoff relativ zu Eisen, und damit auch relativ zueinander, haben sich beispielsweise im Laufe der Zeit nur
wenig geändert. Dies zeigt, daß die Synthese dieser Elemente von der gleichen
Art von Vorläufersternen abhängt. Eisen wird fast ausschließlich in Supernovae
vom Typ Ia synthetisiert und C und N werden hauptsächlich in AGB Sternen
synthetisiert. In beiden Fällen wird die Zunahme der Häufigkeit während der
Entwicklung der Milchstraße durch die langen Lebensdauern der Sterne kleiner und mittlerer Masse bestimmt. Dadurch entwickeln sich die Häufigkeiten
im Gleichschritt, obwohl die Synthese von C und N nichts mit der Synthese
von Fe zu tun hat. Die Häufigkeit von Ni entwickelt sich ebenfalls völlig im
Gleichtakt mit der Eisenhäufigkeit, in diesem Fall, weil Ni genau so wie Fe ganz
überwiegend aus Supernovae vom Typ Ia stammt.
Die Entwicklung der Häufigkeiten von O, Mg, Si, S, Ca und Ti verläuft für
alle diese Elemente sehr ähnlich. Sie werden alle in Supernovae vom Typ II
synthetisiert. Bei sehr kleiner Metallizität spiegelt das Verhältnis [X/Fe] die
Häufigkeit dieser Elemente in den Auswürfen von Supernovaexplosionen wider.
Die Produktion dieser Elemente in Supernovae hängt nur wenig von der Anfangsmetallizität der Vorläufersterne ab (vergl. Abb. 3.12) und deswegen sind
die Häufigkeitsverhältnisse anfangs nahezu konstant. Die Abnahme der Häufigkeitsverhältnisse bei höheren Metallizitäten wird durch den späten Einsatz der
Eisenproduktion durch SN Ia auf Grund der langen Lebensdauer ihrer Vorläufersterne verursacht. Sowie der Beitrag der SN Ia zum Eisenbestand in der Galaxis
anfängt, den Beitrag der SN II zu übersteigen, nimmt das Verhältnis [X/Fe]
kontinuierlich ab.
Ein deutlich anderes Verhalten zeigt Al. Dies wird ebenfalls in SN II synthetisiert, aber nicht direkt aus H und He, sondern aus schon vorhandenen schweren
Kernen. Die Al Synthese setzt deswegen erst mit Verzögerung ein; es muß erst
ein ausreichender Bestand an Vorläuferkernen gebildet sein.
Aus diesen Untersuchungen zur Entwicklung der Elementhäufigkeiten in der
Milchstraße ergibt sich, daß die Häufigkeit der chemischen Elemente in der
Milchstraße sich in sehr gleichförmiger Weise entwickelt. Sterne, die zum gleichen Zeitpunkt in der gleichen Zone in der Milchstraße geboren werden, haben
34
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Abbildung 3.19: Fragment des Murchison Meteoriten, ein primitiver Meteorit mit
Material aus der Entstehungszeit des Sonnensystems vor 4.567 Ga
praktisch innerhalb sehr enger Bandbreiten die gleichen Häufigkeiten. Es gibt
offensichtlich keine Exoten, die zum Zeitpunkt ihrer Entstehung eine völlig abweichende Elementmischung hätten. Es gibt also so etwas wie eine universelle
kosmische Häufigkeit der chemischen Elemente. Nur der Anteil der schweren
Elemente relativ zu den leichten Elementen H und He verändert sich im Laufe
der Zeit. Die relativen Häufigkeiten der schweren Elemente untereinander variiert im Laufe der Zeit nur sehr wenig. Gewisse systematische Abweichungen vom
heutigen Zustand sind bei sehr kleinen Metallizitäten festzustellen, aber dabei
handelt es sich nur um Variationen innerhalb eines Faktors von etwa zwei. Dies
ist im Vergleich zu der Variation der absoluten Häufigkeiten um viele Zehnerpotenzen ein völlig unerheblicher Effekt.
3.4.2
Meteoritische Häufigkeiten
Untersuchungen von Meteoriten haben gezeigt, daß es sich um Gesteinstrümmer
von Körpern aus dem Bereich des Asteroidengürtels handelt. Darunter gibt es
eine Klasse von Objekten, die sog. kohligen Chondriten vom Typ C I, bei denen es sich um 4.6 Ga altes Material aus der Anfangsphase der Entstehung
des Planetensystems handelt. Ein typisches Meteoritenbruchstück eines kohligen Chondriten zeigt Abb. 3.19. Nähere Einzelheiten zum Ursprung und zur
Zusammensetzung der kohligen Chondriten werden später (§ ??) behandelt.
Die Elementhäufigkeiten in diesen Meteoriten können mit normalen chemischen Methoden bestimmt werden. Die Häufigkeiten werden üblicherweise relativ zu der Häufigkeit von Si angegeben, wobei Si eine willkürlich festgesetzte
Häufigkeit von 106 erhält. Zum Vergleich mit Häufigkeitsangaben aus astronomischen Quellen, die ja auf H bezogen sind, muß dann entsprechend der solaren
Si Häufigkeit umgerechnet werden.
Wenn die meteoritischen mit solaren Elementhäufigkeiten verglichen werden, dann stellt man folgendes fest: Für die Masse der Meteoriten findet man
eine ähnliche Elementzusammensetzung wie in der Sonne, aber nicht genau die
gleiche. Einen solchen Fall zeigt der linke Teil der Abb. 3.20. Für die kohligen
Chondriten der Klasse C I, und nur für diese, findet man hingegen fast perfekte
3.4. Kosmische Elementhäufigkeiten
35
Abbildung 3.20: Vergleich meteoritischer mit solaren Elementhäufigkeiten für normale Chondriten (links) und für primitive CI Chondriten (rechts)
Übereinstimmung der Häufigkeiten, wie der rechte Teil der Abb. 3.20 zeigt. Die
wenigen Fälle beträchtlicher Abweichungen zwischen solaren und meteoritschen
Elementhäufigkeiten betreffen flüchtige Elemente, die bevorzugt in der Gasphase
verbleiben und nur teilweise oder fast garnicht in festen Mineralen auskondensieren. Diese kohligen Chondriten vom Typ C I stellen offenbar ein Material dar,
in dem alle schwerflüchtigen Elemente aus dem Material, aus dem die Körper
im Planetensystem und die Sonne entstanden sind, vollständig auskondensiert
sind.
Auf der Basis dieser Feststellung wird angenommen, daß alle schwerflüchtigen Elemente, deren Häufigkeit sich bei der Sonne nicht durch Analyse ihres
Spektrums feststellen läßt, in der Sonne die gleiche Häufigkeit relativ zu Si haben wie in den C I Chondriten. Die Häufigkeit der fehlenden Elemente wird dann
aus diesen Meteoriten bestimmt.
Auf diese Weise kann durch Kombination der Häufigkeitsbestimmungen für
die Sonne und für kohlige Chondriten eine vollständige Tabelle der Elementhäufigkeiten im Sonnensystem konstruiert werden.
3.4.3
Kosmische Elementhäufigkeiten
Die Häufigkeit der 83 stabilen und langlebig radioaktiven Elemente im Sonnensystem zum Zeitpunkt der Entstehung des Sonnensystems ist in Tabelle 3.5
angegeben5 . Die Häufigkeitsangaben stammen entweder aus der Analyse des
Sonnenspektrums oder der chemischen Analyse von Meteoriten, jenachdem für
welche Quelle die genauere Bestimmung möglich ist. Diese Häufigkeitsverteilung
der Elemente wird für repräsentativ im Kosmos gehalten. Sie ist in Abb. 3.21
graphisch dargestellt. Die Metallizität dieser Mischung ist Z = 0.0164.
Die einzige wesentliche Variation mit unterschiedlicher Metallizität ist eine
generelle Verschiebung entsprechend der Häufigkeiten Z der Metalle relativ zu
H und He. Kleine systematische Variationen mit der Metallizität, wie sie in
Abb. 3.18 erkennbar sind, sind für die meisten Betrachtungen nicht erheblich.
Die Zahlenwerte wurden der Tabelle von Grevesse & Sauval [18] entnommen.
Sie beziehen sich auf die Häufigkeit in der protoplanetaren Akkretionsscheibe
5 Neuerdings haben Analysen mit angeblich besseren Methoden eine erhebliche Verringerung der Häufigkeiten von O und C gegenüber den Werten in Tabelle 3.5 ergeben (Asplund
et al. [2]). Dies ist in der Tabelle nicht berücksichtigt, da es starke Zweifel an der Korrektheit
dieser neueren Methoden gibt
36
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Tabelle 3.5: Elementhäufigkeiten ǫi relativ zu H in der Elementmischung des Sonnensystems, Massenkonzentration Xi der Elemente und ihr Anteil fi an der Metallizität.
Daten nach Grevesse & Sauval [18]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
H
He
Li
Be
B
C
N
O
F
Ne
Na
Mg
Al
Si
P
S
Cl
Ar
K
Ca
Sc
Ti
V
Cr
Mn
Fe
Co
Ni
Cu
Zn
Ga
Ge
As
Se
Br
Kr
Rb
Sr
Y
Zr
Nb
Mo
Tc
Ru
Rh
Pd
ǫ
Xi
f
1.000e+00
9.772e-02
2.042e-09
2.630e-11
6.166e-10
3.311e-04
8.318e-05
6.761e-04
3.020e-08
1.202e-04
2.089e-06
3.802e-05
3.090e-06
3.631e-05
2.818e-07
2.138e-05
3.162e-07
2.512e-06
1.349e-07
2.239e-06
1.259e-09
8.710e-08
1.047e-08
4.898e-07
3.388e-07
3.162e-05
8.128e-08
1.820e-06
1.622e-08
3.981e-08
1.349e-09
2.570e-09
2.344e-10
2.570e-09
4.266e-10
2.042e-09
2.570e-10
8.318e-10
1.698e-10
4.074e-10
2.512e-11
9.333e-11
7.088e-01
2.748e-01
9.958e-09
1.666e-10
4.684e-09
2.795e-03
8.186e-04
7.601e-03
4.032e-07
1.705e-03
3.375e-05
6.493e-04
5.859e-05
7.165e-04
6.134e-06
4.817e-04
7.878e-06
7.057e-05
3.706e-06
6.305e-05
3.977e-08
2.929e-06
3.748e-07
1.789e-05
1.308e-05
1.241e-03
3.366e-06
7.505e-05
7.242e-07
1.829e-06
6.609e-08
1.311e-07
1.234e-08
1.426e-07
2.395e-08
1.202e-07
1.544e-08
5.121e-08
1.061e-08
2.611e-08
1.640e-09
6.291e-09
6.084e-07
1.018e-08
2.862e-07
1.707e-01
5.002e-02
4.644e-01
2.463e-05
1.042e-01
2.062e-03
3.967e-02
3.580e-03
4.378e-02
3.748e-04
2.943e-02
4.813e-04
4.312e-03
2.264e-04
3.852e-03
2.430e-06
1.790e-04
2.290e-05
1.093e-03
7.991e-04
7.582e-02
2.057e-04
4.585e-03
4.424e-05
1.118e-04
4.038e-06
8.013e-06
7.540e-07
8.713e-06
1.463e-06
7.345e-06
9.431e-07
3.129e-06
6.482e-07
1.595e-06
1.002e-07
3.844e-07
6.761e-11
1.259e-11
5.012e-11
4.801e-09
9.103e-10
3.748e-09
2.934e-07
5.562e-08
2.290e-07
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
72
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
Ag
Cd
In
Sn
Sb
Te
J
Xe
Cs
Ba
La
Ce
Pr
Nd
Pm
Sm
Eu
Gd
Tb
Dy
Ho
Er
Tm
Yb
Lu
Hf
Ta
Ta
Re
Os
Ir
Pt
Au
Hg
Tl
Pb
Bi
Po
At
Rn
Fr
Ra
Ac
Th
Pa
U
ǫ
Xi
f
1.738e-11
5.754e-11
6.607e-12
1.380e-10
1.072e-11
1.738e-10
3.236e-11
1.479e-10
1.349e-11
1.660e-10
1.660e-11
4.266e-11
6.310e-12
3.090e-11
1.317e-09
4.545e-09
5.330e-10
1.151e-08
9.168e-10
1.558e-08
2.886e-09
1.365e-08
1.260e-09
1.601e-08
1.620e-09
4.200e-09
6.247e-10
3.132e-09
8.048e-08
2.777e-07
3.257e-08
7.035e-07
5.601e-08
9.520e-07
1.763e-07
8.337e-07
7.697e-08
9.784e-07
9.897e-08
2.566e-07
3.817e-08
1.914e-07
9.550e-12
3.548e-12
1.230e-11
2.239e-12
1.479e-11
3.236e-12
9.333e-12
1.413e-12
9.120e-12
1.349e-12
5.623e-12
7.413e-13
7.413e-13
1.905e-12
2.455e-11
2.344e-11
4.898e-11
7.079e-12
7.079e-12
6.761e-12
1.148e-10
5.129e-12
1.009e-09
3.789e-10
1.359e-09
2.500e-10
1.689e-09
3.750e-10
1.097e-09
1.677e-10
1.109e-09
1.658e-10
7.053e-10
9.426e-11
9.426e-11
2.493e-10
3.281e-09
3.166e-09
6.714e-09
9.798e-10
9.978e-10
9.710e-10
1.672e-08
7.531e-10
6.165e-08
2.315e-08
8.305e-08
1.527e-08
1.032e-07
2.291e-08
6.701e-08
1.024e-08
6.775e-08
1.013e-08
4.309e-08
5.759e-09
5.759e-09
1.523e-08
2.005e-07
1.934e-07
4.102e-07
5.986e-08
6.097e-08
5.932e-08
1.021e-06
4.601e-08
1.230e-12
2.006e-10
1.226e-08
3.162e-13
5.289e-11
3.231e-09
3.4. Kosmische Elementhäufigkeiten
12
37
H
He
10
O
C
Ne
8
Si
Mg
N
Fe
S
εel
Ar
Ca
Al
Na
6
P
Ti Mn
Cl
Zn
Co
K
F
4
Ni
Cr
Cu
V
Li
B
Sc
2
Be
0
0
10
20
Ge
Se
Kr
Sr
Zr
Xe
Ga
Mo Pd SnTe Ba
Pb
Br
Ru Cd
Ce
As Rb
Pt
Dy
Nd
Os
Yb
Y
Gd
Hg
Sm
Er
Hf
J
Nb
W Ir
Ag
La
Rh InSb Cs
Au Tl Bi
Pr
Eu Ho
Tb
Lu Re
Tm Ta
30
40
50
60
70
80
Th
U
90
100
Z
Abbildung 3.21: Häufigkeitsverteilung der Elemente im Sonnensystem (dekadischer
Logarithmus), wie sie aus der Analyse des Sonnenspektrums und den Häufigkeitsbestimmungen in Meteoriten folgt (Grevesse & Sauval [18]). Die Häufigkeit ist in der
astronomischen Häufigkeitsskala angegeben, in der H die Häufigkeit 12 erhält.
zum Zeitpunkt der Entstehung der Sonne. In der heutigen Sonne haben He und
Li geringere Häufigkeiten als in der Tabelle angegeben. Lithium hat eine erheblich kleinere Häufigkeit, weil Li in der Protosonne weitgehend verbrannt wurde.
Die He Häufigkeit hat seit der Bildung der Sonne durch Sedimentationseffekte
geringfügig abgenommen.
Die relativen Beiträge fi der einzelnen schweren Elemente i zur Metallizität
log f
-3
-2
-1
0
O
C
Fe
Ne
Si
Mg
N
S
Ni
Ca
Al
Ar
Na
Cr
Mn
Abbildung 3.22: Beiträge der Elemente schwerer als He zur Metallizität der Sterne.
Dargestellt ist der Massenanteil f der Elemente an der gesamten Metallizität..
38
Kapitel 3. Kosmische und solare Elementhäufigkeiten
Z sind in Abb. 3.22 dargestellt; numerische Werte finden sich in Tabelle 3.5. Der
Löwenanteil an den schweren Elementen in der heutigen kosmischen Elementmischung, etwa 80%, entfällt auf nur vier Elemente: O, C, Fe und Ne. Weitere 16%
entfallen auf die vier Elemente Si, Mg, N und S. Sämtliche anderen schweren
Elemente zusammen haben nur einen Massenanteil von 4%
Für den Aufbau aller derjenigen Körper im Sonnensystem, und entsprechend
auch in extrasolaren Planetensystemen, die hauptsächlich aus den schwerflüchtigen Elementen bestehen, sind wegen dieser sehr ungleichmäßigen Verteilung der
Häufigkeiten nur sehr wenige Elemente wichtig. Das sind die gerade genannten
ohne Ne und N, denn die beiden letzteren sind flüchtige Elemente, die praktisch
vollständig in der Gasphase verbleiben. Einige wenige weitere Elemente wie
Al, Ca, Na und Ni spielen noch bei einigen Fragestellungen eine gewisse Rolle,
alle weiteren Elemente spielen für den Aufbau der Planeten keine Rolle. Wegen der Universalität der kosmischen Häufigkeitsverteilung sind keine größeren
Variationen in der Zusammensetzung der festen Körper in extrasolaren Planetensystemen gegenüber der im Sonnensystem zu erwarten.
3.4.4
Langlebige radioaktive Isotope
Langlebige radioaktive Nuklide sind aus zwei Gründen von Interesse. Zum einen
sind sie wegen der beim Zerfall freigesetzten Energie eine wichtige Wärmequelle
für Planeten. Zum anderen können sie dazu verwendet werden, das Alter von
Gesteinsproben zu datieren.
Tabelle 3.6 gibt alle Nuklide mit Halbwertszeiten größer als 105 Jahre an.
Alle Nuklide mit Halbwertszeiten von mindestens etwa 109 Jahren sind seit
der Entstehung des Sonnensystems vor 4.57 Ga noch nicht restlos zerfallen,
wenn sie in der interstellaren Materie vorhanden waren; sie sind auch tatsächlich
alle noch heute im Sonnensystem aktiv. Nuklide mit Halbwertszeiten kürzer als
ca. 105 a sind während der Zeitdauer der Kollapsphase bei der Entstehung des
Sonnensystems bereits restlos zerfallen. Da das Sonnensystem seit dem Kollaps
von der interstellaren Materie isoliert ist, können solche Nuklide später nicht
mehr von außen in das Sonnensystem eingetragen werde, es sei denn, daß sich
in der näheren Umgebung der Sonne eine Supernovaexplosion ereignet. Da es
im Sonnensystem selbst keine effizienten Prozesse zur Erzeugung radioaktiver
Isotope zu geben scheint, sind Nuklide mit kürzeren Zerfallszeiten als ca. 105
Jahre nach derzeitigem Kenntnisstand nicht von Interesse.
Nuklide mit Zerfallszeiten zwischen etwa 105 Jahren und einigen 108 Jahren
können im heutigen Sonnensystem nicht mehr aktiv sein, sie könnten aber im
frühen Sonnensystem existiert haben, wenn sie in der Materie der Molekülwolke
vorhanden waren, aus der das Sonnensystem entstanden ist. Tatsächlich sind
die Zerfallsprodukte fast aller dieser Nuklide in meteorischem Material nachgewiesen worden.
3.4. Kosmische Elementhäufigkeiten
39
Tabelle 3.6: Langlebige radioaktive Nuklide mit Halbwertszeiten τ1/2 größer als 105
Jahre, Zerfallsenergie E, Art des Zerfalls und relative Häufigkeit bei mehr als einem
Zerfallskanal, sowie die Häufigkeit zum Zeitpunkt der Entstehung des Sonnensystems
relativ zu einem Referenzkern
Z
A
El
τ1/2
Jahre
MeV
0.556
4.004
3.890
0.709
0.115
1.312
1.500
0.421
0.597
0.237
0.281
0.283
0.091
2.006
0.320
1.800
0.294
0.033
0.495
0.380
0.051
0.194
0.269
0.640
2.500
2.230
2.730
2.950
1.192
0.370
0.003
0.051
2.880
4.081
4.909
4.865
4.679
4.569
4.180
0.940
4.957
4.983
4.665
5.352
5.162
4
13
10
26
Be
Al
1.52·106
7.10·105
17
36
Cl
3.01·105
19
40
20
25
26
36
37
40
41
43
43
43
46
49
50
52
53
55
57
62
62
64
66
71
71
75
82
83
90
92
92
92
92
92
93
93
94
94
96
96
41
53
60
81
87
93
92
97
98
99
107
115
126
123
129
135
138
146
147
150
154
176
182
187
205
208
232
233
234
235
236
238
236
237
242
244
247
248
E
K
1.26·109
Ca
Mn
Fe
Kr
Rb
Zr
Nb
Tc
Tc
Tc
Pd
In
Sn
Te
I
Cs
La
Sm
Sm
Gd
Dy
Lu
Hf
Re
Pb
Bi
Th
U
U
U
U
U
Np
Np
Pu
Pu
Cm
Cm
1.02·105
3.70·106
1.50·106
2.20·105
4.88·1010
1.50·106
3.70·107
2.60·106
4.20·106
2.13·105
6.50·106
4.40·1014
1.00·105
1.30·1013
1.70·107
2.30·106
1.06·1011
1.03·106
1.06·1011
1.80·106
3.00·106
3.80·1010
9.00·106
4.40·1010
1.51·107
3.68·105
1.40·1010
1.59·105
2.45·105
7.04·108
2.34·107
4.46·109
1.55·105
2.14·105
3.76·105
8.20·107
1.56·107
3.40·105
Zerfallsart
%
β−
β+
EC
β−
β+
β−
β+
EC
EC
β−
EC
β−
β−
EC
EC
β−
β−
β−
β−
β−
β−
β−
β−
β−
α
α
α
α
β−
β−
β−
EC
EC
α
α
α
α
α
α
EC
α
α
α
α
α
82
18
98
2
89
11
Anfangshäufigkeit
f
∼ 10−3
5 × 10−5
∼ 10−4
2.0 × 10−10
1.5 × 10−8
1.4 × 10−5
2 × 10−7
7.6 × 10−11
Ref. Nukl.
10
26
36
Cl/35 Cl
K/1 H
40
41
Ca/40 Ca
Mn/55 Mn
60
Fe/56 Fe
53
87
< 2 × 10−5
92
∼ 10−4
4.5 × 10−5
6.3 × 10−13
107
1.5 × 10−12
∼ 10−4
Be/9 Be
Al/27 Al
Rb/1 H
Nb/92 Nb
99
Tc/99 Ru
Pd/108 Pd
115
In/1 H
123
Te/1 H
I/127 I
129
138
La/1 H
Sm/144 Sm
147
Sm/1 H
1.5 × 10−14
5 × 10−3
1.4 × 10−12
146
3.7 × 10−14
1 ∼ 10−4
1.3 × 10−12
3 × 10−4
Lu/1 H
Hf/180 Hf
187
Re/1 H
205
Pb/204 Pb
2.6 × 10−12
176
182
232
Th/1 H
1.5 × 10−12
235
8.9 × 10−13
238
7 × 10−3
244
U/1 H
U /1 H
Pu/238 U
40