8 Untere Schranke für vergleichende Sortierver

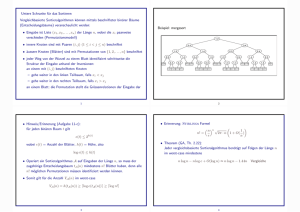
8
Untere Schranke für vergleichende Sortierverfahren
Viele verwendete schnelle Sortierverfahren (z.B.: MERGESORT, HEAPSORT )
besitzen eine Laufzeit von O(n log n). Die Frage, die sich dabei stellt, lautet:
Geht es besser?
Man kann beweisen, dass jedes Sortierverfahren, das mittels Vergleichen arbeitet1 , mindestens c · n log n Vergleiche im worst case braucht (wobei c > 0 und
konstant ist).
8.1
Herleiten der unteren Schranke Ω (n log n)
Der Kontrolluss eines vergleichenden Sortierverfahrens kann mittels eines sogenannten Entscheidungsbaummodells dargestellt werden. Darin scheinen alle
möglichen und nötigen Entscheidungen auf, um ein sortiertes lineares Feld zu
erhalten. Beispiel: Es liegt eine Sequenz von 3 Zahlen vor < a1 , a2 , a3 > (z.B.
< 5, 8, 2 >). Dann schaut der zugehörige Entscheidungsbaum folgendermaÿen
aus:
Die Blätter stellen alle möglichen Permutationen des Inputs dar. Die Anzahl
der Blätter ist daher gleich n!.
Das worst-case Verhalten entspricht dem längsten Ast im Entscheidungsbaum
(Anzahl der inneren Knoten = Anzahl der Vergleiche). Der ideale Sortieralgorithmus enspricht einem vollständigen, ausgeglichenen Baum. Dadurch wird der
längste Ast ( = worst case) minimiert. Die Höhe beträgt h ≥ log(n!). Mit Hilfe
der Stirling-Approximation n! > ( ne )n erhält man:
h ≥ log
1 D.h.,
n n
e
= n · log n − n · log e = Ω(n · log n)
bei dem die Information über die korrekte Anordnung der Elemente dadurch gewon-
nen wird, dass jeweils einzelne Elemente direkt miteinander verglichen werden.
1
Ω(n · log n) ist die untere Schranke für die Anzahl der im worst case zum
Sortieren notwendigen Vergleiche (und somit für die worst case Laufzeit vergleichender Sortierverfahren).
8.2
worst-case optimal
Im Zusammenhang der unteren Schranke kann einen Sortieralgorithmus als
worst-case optimal bezeichnen, wenn er für jede Eingabefolge in O(n · log n)
sortiert. Zum Beispiel sind MERGESORT und HEAPSORT worst-case optimal.
8.3
Sortieren durch Fachverteilung (RadixSort)
RadixSort ist ein Beispiel für ein nicht vergleichsbasiertes Sortierverfahren.
Nicht vergleichsbasierte Sortierverfahren arbeiten ohne Vergleiche und müssen
daher zusätzliche Annahmen über den Input machen. Der Input zu RadixSort
besteht aus n Dezimalzahlen der Länge d.
RADIXSORT (A,d)
1: FOR i = 1 TO d DO
2:
Ordne A nach i-ter Ziffer von hinten in Fächer ein
3:
Fasse die Fächer in aufsteigender Reihenfolge wieder in A
zusammen
Zeile 2 wird Streuphase genannt, und Zeile 3 bezeichnet man auch als Sam. RadixSort ist korrekt, weil nach den ersten k Durchläufen die Zahlen,
eingeschränkt auf die letzten k Ziern, sortiert sind. Eine wichtige Bedingung
für die Korrektheit der Sammelphase ist, dass die vorige Reihenfolge innerhalb
der Fächer aufrechterhalten werden muss. Diese Eigenschaft eines Sortieralgorithmus, dass Elemente mit identischen Sortierschlüsseln in Input und Output
in gleicher Reihenfolge erscheinen, nennt man Stabilität.
Die Laufzeit von RadixSort betragt T (n) = O(d·n), ist also linear, wenn d als
konstant betrachtet wird. In diesem Fall ist RadixSort asymptotisch schneller als
vergleichsbasierte Sortierverfahren, wie z.B. QuickSort, hat aber einen erhöhten
Speicherbedarf.
melphase
2