Elementarteilchenphysik

Elementarteilchenphysik
Notizen zur Vorlesung ES 2002/2003
24. Februar 2003 100
TEIL II: KAPITEL 6-10
Autoren: V. Blobel, A. Meyer, B. Naroska
Institut für Experimentalphysik
Universität Hamburg
WS 2002/03
ii
Physikalische Konstanten1
a
b
c
d
e
f
g
h
j
Größe
Lichtgeschwindigkeit im Vakuuma
Plancksche Konstante
Plancksche Konstante, reduziert
Symbol, Gleichung
c
h
h̄
Elementarladung
e
Umrechnungsfaktor
Umrechnungsfaktor
Elektronenmasse
h̄c
(h̄c)2
me
Protonmasse
mp
Deuteronmasse
Atomare Masseneinheitb
md
(1g)/(NA Mol)
permittivity of free spacec
permeability of free spacec
ε0
µ0
Feinstrukturkonstanted
Klassischer Elektronenradius
Comptonwellenlänge des Elektrons
Bohrscher Radiuse
Wellenlänge eines 1 eV-Teilchens
Rydberg-Energiee
Thomson-Wirkungsquerschnitt
Bohrsches Magneton
Kernmagneton
Zyklotronfrequenz/Feld (Elektron)
Zyklotronfrequenz/Feld (Proton)
Gravitationskonstantef
α = e2 /4πε0 h̄c
re = e2 /4πε0 me c2
λe /2π = h̄/me c = re α−1
a∞ = re α−2
hc/e
hcR∞ = me c2 α2 /2
σT = 8πre2 /3
µB = eh̄/2me
µN = eh̄/2mp
e
/B = e/me
ωcycl
p
ωcycl
/B = e/me
GN
Standard-Gravitationsbeschleunigungg
Avogadrosche Zahl
Boltzmann-Konstante
g
NA
k
Molarvolumenh
Wiensche Konstante
Stefan-Boltzmann-Konstante
Fermi Kopplungskonstante
Schwacher Mischungswinkel
W ± Bosonenmasse
Z 0 Bosonenmasse
Kopplungskonst. der starken WW
NA k(273.15)/101325Pa)
b = λTmax
σ = π 2 k 4 /60h̄3 c2
GF /(h̄c)3
sin2 ϑ(MZ )
mW
mZ
αs (MZ )
Wert
299 792 458 m s−1
6.6260755(40) × 10−34 J s
1.05457266(63) × 10−34 J s
6.5821220(20) × 10−22 MeV s
1.60217733(49) × 10−19 C
4.8032068(15) × 10−10 esu
197.327053(59) MeV fm
0.38937966(23) GeV2 mbarn
0.51099906(15) MeV/c2
9.1093897(54) × 10−31 kg
938.27231(28) MeV/c2
1.6726231(10) × 10−27 kg
1.007276470(12) u
1836.152701(37) me
1875.61339(57) MeV/c2
931.49432(28) MeV/c2
931.49432(28) MeV c2
1.6605402(10) × 10−27 kg
8.854187817 . . . × 10−12 F m−1
4π × 10−7 N A−2
12.566370614 . . . × 10−7 N A−2
1/137.0359895(61)
2.81794092(38) × 10−15 m
3.86159323(35) × 10−13 m
0.529177249(24) × 10−10 m
1.23984244(37) × 10−6 m
13.6056981(40) eV
0.66524616(18) barn
5.78838263(52) × 10−11 MeV T−1
3.15245166(28) × 10−14 MeV T−1
1.75881962(53) × 1011 rad s−1 T−1
9.5788309(29) × 107 rad s−1 T−1
6.67259(85) × 10−11 m3 kg−1 s−2
6.70711(86) × 10−39 h̄c(Gev/c 2 )−2
9.80665 m s−2
6.0221367(36) × 1023 mol−1
1.380658(12) × 10−23 JK−1
8.617385(73) × 10−5 eV K−1
22.41410(19) × 10−3 m3 mol−1
2.897756(24) × 10−3 m K
5.67051(19) × 10−8 W m−2 K−4
1.16639(1) × 10−5 GeV−2
0.23124(24)
80.41(10) GeV/c2
91.187(7) GeV/c2
0.119(2)
Exakt. Das Meter ist die Strecke, die Licht im Vakuum im 1/299792458 Teil einer Sekunde zurücklegt.
Masse des 12 C-Atoms/12.
Exakt. ε0 µ0 = 1/c2 .
Bei Q2 = 0. Bei Q2 ≈ m2W ist der Wert etwa 1/128.
Kernmasse ∞ angenommen.
Absolute Messungen von GN im Labor gibt es nur bei Entfernungen 10−1±1 m.
Exakt. Auf Meereshöhe.
Ideales Gas bei STP.
Im M S Schema.
1
Grundlage ist ”1986 Adjustment of the Fundamental Physical Constants” by E.R. Cohen and B.N. Taylor,
Rev. Mod. Phys. 59, 1121 (1987). Der gesamte Satz der 1986 Konstanten (und eventueller neuer Werte) ist zu
finden unter http://physics.nist.gov/cuu. Die letzte Gruppe von Konstanten stammt aus der Review of Particle
Physics, The European Physical Journal C, 1998.
Inhaltsverzeichnis
LITERATUR . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . vii
1 Einführung
1.1 Die Teilchen des Standardmodells . . . . . .
1.1.1 Elektron . . . . . . . . . . . . . . . .
1.1.2 Photon . . . . . . . . . . . . . . . . .
1.1.3 Antiteilchen; Positron e+ . . . . . . .
1.1.4 Elektron-Neutrino und Antineutrino
1.1.5 Weitere Leptonenfamilien . . . . . .
1.1.6 Hadronen, Quarks . . . . . . . . . .
1.1.7 Baryonenzahl . . . . . . . . . . . . .
1.1.8 Quarks . . . . . . . . . . . . . . . . .
1.2 Wechselwirkungen und Feynman-Diagramme
1.2.1 Kräfte, Teilchenaustausch, Reichweite
1.2.2 Das Yukawa Potential . . . . . . . .
1.3 Relativistische Wellengleichungen . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Relativistische Kinematik
2.1 Spezielle Relativitätstheorie . . . . . . . . . . . . . . .
2.1.1 Lorentztransformation . . . . . . . . . . . . . .
2.1.2 Vierervektoren . . . . . . . . . . . . . . . . . .
2.1.3 Energie und Impuls . . . . . . . . . . . . . . . .
2.1.4 Einheiten und Dimensionen . . . . . . . . . . .
2.2 Teilchen-Reaktionen und -Zerfälle . . . . . . . . . . . .
2.2.1 Kinematik von Teilchenreaktionen . . . . . . . .
2.2.2 Wirkungsquerschnitt . . . . . . . . . . . . . . .
2.3 ∗ Quantenmechanische Berechnung von Übergangsraten
2.3.1 Goldene Regel . . . . . . . . . . . . . . . . . . .
2.3.2 Flußfaktor und Wirkungsquerschnitt . . . . . .
2.3.3 Teilchenzerfälle . . . . . . . . . . . . . . . . . .
Glossar . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3 Teilchenbeschleuniger
3.1 Einleitung . . . . . . . . . . . . . . . . . . . . . . .
3.2 Strahloptik und Betatronschwingungen . . . . . . .
3.3 Beschleunigung und Synchrotronschwingungen . . .
3.4 Synchrotronstrahlung . . . . . . . . . . . . . . . . .
3.4.1 Strahlungsdämpfung und Quantenanregung.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
3
3
4
4
4
4
6
6
7
7
7
8
10
.
.
.
.
.
.
.
.
.
.
.
.
.
13
13
13
15
16
18
18
19
26
29
30
34
35
40
.
.
.
.
.
43
43
43
48
50
51
iv
INHALTSVERZEICHNIS
3.5 Teilchenquellen und Vorbeschleuniger . .
3.5.1 Kreisförmige und lineare Collider
3.6 Kosmische Beschleuniger . . . . . . . . .
3.7 Einige Beschleunigeranlagen . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
52
53
54
56
4 Erhaltungssätze und Symmetrien
4.1 Symmetrieeigenschaften . . . . . . . . . . . . . . . . . . . . . .
4.1.1 Räumliche Translation und Impulserhaltung . . . . . . .
4.2 Drehimpuls . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.2.1 Addition von Drehimpulsen . . . . . . . . . . . . . . . .
4.2.2 Spin-Statistik-Theorem . . . . . . . . . . . . . . . . . . .
4.2.3 Spin 1/2 . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3 Isospin und Flavour-Symmetrien . . . . . . . . . . . . . . . . . .
4.3.1 Interim: Entdeckung der Seltsamkeit . . . . . . . . . . .
4.3.2 Isospin . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.3.3 Isospin und das π-N -System . . . . . . . . . . . . . . . .
4.4 Diskrete Symmetrien . . . . . . . . . . . . . . . . . . . . . . . .
4.5 Parität . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.5.1 Parität von Drehimpulszuständen . . . . . . . . . . . . .
4.5.2 Parität von Fermionen und Antifermionen . . . . . . . .
4.5.3 Das elektromagnetische Feld und Photonen . . . . . . . .
4.5.4 Die Eigenparität des π − . . . . . . . . . . . . . . . . . .
4.5.5 Quarkmodell . . . . . . . . . . . . . . . . . . . . . . . .
4.6 Paritätsverletzung in der schwachen Wechselwirkung . . . . . .
4.7 Ladungskonjugation . . . . . . . . . . . . . . . . . . . . . . . .
4.7.1 C-Parität . . . . . . . . . . . . . . . . . . . . . . . . . .
4.7.2 Experimentelle Tests der C-Invarianz . . . . . . . . . . .
4.7.3 Verletzung der C-Invarianz in schwacher Wechselwirkung
4.7.4 G-Parität∗ . . . . . . . . . . . . . . . . . . . . . . . . . .
4.8 CP -Eigenzustände und die neutralen K-Mesonen . . . . . . . .
4.8.1 CP -Eigenzustände . . . . . . . . . . . . . . . . . . . . .
4.8.2 Oszillationen der Seltsamkeit . . . . . . . . . . . . . . .
4.8.3 K 0 -Regeneration . . . . . . . . . . . . . . . . . . . . . .
4.9 CP -Verletzung . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.10 Zeitumkehr . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.11 Das CP T -Theorem . . . . . . . . . . . . . . . . . . . . . . . . .
4.12 Zusammenfassung und Quantenzahlen . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
59
59
61
62
65
68
69
70
70
72
74
78
78
80
80
81
81
82
82
85
85
86
87
87
88
88
90
91
92
93
95
96
.
.
.
.
.
.
.
.
97
97
97
98
101
102
103
105
107
5 Teilchennachweis und Detektoren
5.1 Wechselwirkung von Teilchen mit Materie . . . . . . . . . . . . . .
5.1.1 Wechselwirkung schwerer geladener Teilchen: IONISATION
Eigenschaften der Bethe–Bloch Formel . . . . . . . . . . . .
5.1.2 Vielfachstreuung . . . . . . . . . . . . . . . . . . . . . . . .
5.1.3 Čerenkovstrahlung . . . . . . . . . . . . . . . . . . . . . . .
5.1.4 Energieverlust von Elektronen: Bremsstrahlung . . . . . . .
5.1.5 Wechselwirkung von Photonen mit Materie . . . . . . . . . .
5.1.6 Starke Wechselwirkung von Teilchen mit Materie . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
INHALTSVERZEICHNIS
5.2 Spurdetektoren für geladene Teilchen . . . . . . . . . .
5.2.1 Impulsmessung . . . . . . . . . . . . . . . . . .
5.2.2 Szintillatoren . . . . . . . . . . . . . . . . . . .
5.2.3 Blasenkammer . . . . . . . . . . . . . . . . . . .
5.2.4 Proportional- und Driftkammern . . . . . . . .
5.2.5 Halbleiterdetektoren/Mikro-Vertexdetektoren .
5.3 Kalorimeter . . . . . . . . . . . . . . . . . . . . . . . .
5.3.1 Elektromagnetische Kalorimeter (Schauerzähler)
5.3.2 Hadronische Kalorimeter . . . . . . . . . . . . .
5.3.3 Ein Speicherringdetektor . . . . . . . . . . . . .
v
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
108
108
109
110
111
114
115
115
117
118
6 Feynmandiagramme und Test der QED
6.1 Teilchen-Antiteilchen . . . . . . . . . . . . . . . . . . . . . . . . .
6.2 Elementare Prozesse und Feynman-Graphen in der QED . . . . .
6.3 Einige Reaktionen und Tests der QED . . . . . . . . . . . . . . .
6.3.1 Feynmanregeln und Berechnung von σ (e+ e− → µ+ µ− ) .
6.3.2 Der Bosonpropagator . . . . . . . . . . . . . . . . . . . . .
6.3.3 Test der QED: anomales magnetisches Moment des Myons
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
121
121
123
125
129
130
131
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
135
135
135
140
141
141
144
146
147
149
151
153
153
155
155
159
.
.
.
.
.
.
.
.
.
.
161
161
162
162
163
164
166
167
169
171
174
7 Quarks und Hadronen
7.1 Einleitung . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.2 Die Entdeckung der schweren Quarks . . . . . . . . . . . .
7.3 Die leichten Hadronen . . . . . . . . . . . . . . . . . . . .
7.3.1 Die leichten Mesonen . . . . . . . . . . . . . . . . .
7.3.2 Die leichten Baryonen . . . . . . . . . . . . . . . .
7.3.3 Massenaufspaltung der Baryonen Supermultipletts.
7.4 Farbe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.4.1 Farbladungen und Confinement . . . . . . . . . . .
7.5 Gluonen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7.5.1 e+ e− →Hadronen . . . . . . . . . . . . . . . . . .
7.5.2 Hadronisierung . . . . . . . . . . . . . . . . . . . .
7.5.3 Entdeckung der Gluonen . . . . . . . . . . . . . . .
7.5.4 Spin des Gluons . . . . . . . . . . . . . . . . . . . .
7.6 Die “laufende” starke Kopplung αs . . . . . . . . . . . . .
7.7 Nochmal: Zerfall des J/ψ . . . . . . . . . . . . . . . . . .
8 Tiefunelastische Streuung: Struktur des Nukleons
8.1 Einleitung . . . . . . . . . . . . . . . . . . . . . . . . .
8.2 Elastische Streuung . . . . . . . . . . . . . . . . . . . .
8.2.1 Elastische Streuung an Punktladungen . . . . .
8.2.2 Elastische Streuung an einer Ladungsverteilung
8.2.3 Elastische Elektron Proton Streuung . . . . . .
8.3 Unelastische Streuung . . . . . . . . . . . . . . . . . .
8.3.1 Kinematik von unelastischer Streuung . . . . .
8.3.2 Quark Parton Modell . . . . . . . . . . . . . . .
8.3.3 Quarkverteilungen im Nukleon . . . . . . . . . .
8.3.4 Quarkladungen . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
vi
INHALTSVERZEICHNIS
8.3.5 Quarkimpulssummen . . . . . . . . . .
8.4 Gluonen . . . . . . . . . . . . . . . . . . . . .
8.4.1 Strukturfunktion F2 (x, Q2 ) bei HERA
8.4.2 QCD-Dynamik . . . . . . . . . . . . .
8.4.3 QCD-Konsistenztests . . . . . . . . . .
8.5 Die Suche nach Quarksubstruktur . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
175
175
177
178
183
183
9 Schwache Wechselwirkungen
9.1 Zerfall des Pions und Struktur der schwachen Wechselwirkung . . . . . . .
9.2 Neutrinostrahlen und Entdeckung der neutralen schwachen Wechselwirkung
9.3 Universalität der schwachen Wechselwirkung . . . . . . . . . . . . . . . . .
9.3.1 Leptonuniversalität . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.3.2 Fermi-Kopplungskonstante . . . . . . . . . . . . . . . . . . . . . . .
9.3.3 Schwache Wechselwirkung von Quarks . . . . . . . . . . . . . . . .
9.4 Die Z 0 und W ± Bosonen . . . . . . . . . . . . . . . . . . . . . . . . . . .
9.4.1 Entdeckung der Z 0 und W ± Bosonen . . . . . . . . . . . . . . . .
9.4.2 Paritätsverletzung beim W Zerfall . . . . . . . . . . . . . . . . . . .
9.4.3 Präzisionsvermessung des W Bosons . . . . . . . . . . . . . . . . .
9.4.4 Z 0 Produktion an e+ e− Speicherringen . . . . . . . . . . . . . . .
9.4.5 Anzahl der Neutrinos . . . . . . . . . . . . . . . . . . . . . . . . . .
9.5 Mischung von 3 Familien: CP Verletzung und Top Quark . . . . . . . . . .
9.5.1 Entdeckung des Top Quarks . . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
187
188
191
194
194
196
196
199
200
203
205
207
211
213
215
10 Neutrinophysik
10.1 Neutrino Entdeckung und Nachweis . . . . . .
10.2 Bestimmung der Neutrinomasse . . . . . . . .
10.3 Neutrino mass and oscillations . . . . . . . . .
10.3.1 Dirac and Majorana mass . . . . . . .
10.3.2 Neutrino oscillations (Zeitentwicklung)
10.4 Experimente zu Neutrino Oszillationen . . . .
10.5 Neutrinos von der Sonne . . . . . . . . . . . .
Nachweis . . . . . . . . . . . . . . . . .
10.5.1 Sudbury Neutrino Observatory (SNO)
10.6 Atmosphärische Neutrinos . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
221
221
223
225
225
226
228
229
229
233
235
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Kapitel 6
Feynmandiagramme und Test der QED
Es ist üblich geworden, Reaktionen durch Feynmandiagramme darzustellen. Diese sind von
Feynman für die QED entwickelt worden, sind dann aber auf alle Wechselwirkungen übertragen
worden (bis auf Gravitation). Sie veranschaulichen in einfacher und übersichtlicher Weise das
Bild, welches man sich von einer Wechselwirkung macht.
In Kapitel 1.3 wurde die Klein-Gordon Gleichung als erster Versuch einer relativistischen Beschreibung der Quantenmechanik hingeschrieben. Das Problem dabei bestand darin, daß negative Energien als Lösung der Wellengleichung möglich sind. Die später formulierte Dirac
Gleichung konnte dies auch nicht beseitigen.
6.1
Teilchen-Antiteilchen
Eine Interpretation zur Lösungen der Diracgleichung mit negativer Energie stammt von Stückelberg
und Feynman. Danach besitzen die Wellenfunktionen mit negativen Energiewerten selber keine physikalische Signifikanz, erhalten sie aber dadurch, daß man die Zeitrichtung umkehrt.
Sie entsprechen dann den Wellenfunktionen von Antiteilchen, die mit positiver Energie zeitlich vorwärts laufen. Wir wollen die mathematischen Details dieser Zeitumkehrtransformation
nicht vorführen, sondern die Stückelberg-Feynman-Ideen an einigen Beispielen verdeutlichen.
Ein Elektron, das mit negativer Energie rückwärts in der Zeit vom Punkt 2 zum Punkt 1 bewegt
wird (Abb. 6.1a), entspricht physikalisch einem Positron, das mit positiver Energie vorwärts in
der Zeit vom Punkt 1 zu Punkt 2 fliegt (Abb. 6.1b).
t
t
2)
2)
e+
e-
E+ = + E > 0
E- = - E < 0
1)
a)
1)
x
b)
x
Abbildung 6.1: (a) Bewegung eines Elektrons negativer Energie rückwärts in der Zeit, (b)
Interpretation als Bewegung eines Positrons mit positiver Energie vorwärts in der Zeit.
122
Feynmandiagramme und Test der QED
e-
E2 > 0
e-
E2 < 0
e+
E ’2 > 0
e+
E 1’ = - E 1> 0
=
Wechselwirkung
mit Potential
e-
e-
E1 > 0
E1 < 0
a)
b)
e-
=
e-
e-
e-
e+
E1 > 0
E2 < 0
E1 > 0
E ’2 > 0
c)
e-
e+
e-
=
E1 < 0
E ’1 > 0
E2 > 0
E2 > 0
d)
Abbildung 6.2: (a) Diagramm für Elektronenstreuung an einem Potential; (b) PositronStreuung; (c) Elektron-Positron-Vernichtung; (d) Elektron-Positron-Erzeugung.
Nun betrachten wir Wechselwirkungen mit einem Potential. Abbildung 6.2a zeigt die Streuung
eines normalen Elektrons (E > 0) an diesem Potential. Die Streuung eines Elektrons mit
negativer Energie (E1 < 0), das rückwärts in der Zeit läuft (Abb. 6.2b ) ist äquivalent zur
Streuung eines Positrons mit positiver Energie (E1 < 0, E10 > 0), das vorwärts in der Zeit
läuft.
Es sind noch zwei weitere Prozesse denkbar, und hier zeigt sich die wahre Stärke der StückelbergFeynman-Interpretation: Ein Elektron mit E1 > 0 werde durch das Potential in einen Zustand gestreut, der sich mit negativer Energie zeitlich rückwärts bewegt (Abb. 6.2c ). Dies
entspricht der Annihilation eines Elektron-Positron-Paares, wobei das Potential Energie aufnimmt. Schließlich kann ein zeitlich rückwärts laufendes Elektron negativer Energie durch das
Potential in einen vorwärts laufenden Zustand mit positiver Energie gestreut werden (Abb.
6.2d ). Dies ist äquivalent zur Erzeugung eines Elektron-Positron-Paares, wobei das Potential
Energie abgibt (ein γ-Quant der Energie Eγ > 2m c2 ).
Die Feynman-Diagramme und -Regeln basieren auf der Stückelberg-Feynman-Interpretation
der Wellenfunktionen negativer Energie und behandeln alle vier Prozesse: Elektron-Streuung,
Positron-Streuung, Paar-Vernichtung und Paar-Erzeugung mit ein und demselben mathematischen Formalismus. Wie wir gesehen haben, folgt die Existenz der Antiteilchen aus der Vereinigung von Relativitätstheorie und Quantentheorie. Die Dirac-Gleichung wurde ursprünglich
als Wellengleichung eines einzelnen Elektrons konzipiert, ist aber im Prinzip eine Vielteilchengleichung, da bei hinreichend hohen Energien beliebig viele Teilchen-Antiteilchen-Paare erzeugt
oder vernichtet werden können. Die Antiteilchen sind in der Art der Wechselwirkung und in
den Werten von Spin, mittlerer Lebensdauer und Masse identisch mit den Teilchen. Alle ladungsartigen Quantenzahlen haben das entgegengesetzte Vorzeichen.
6.2 Elementare Prozesse und Feynman-Graphen in der QED
6.2
123
Elementare Prozesse und Feynman-Graphen in der
QED
In der Teilchenphysik wird die Wechselwirkung meist nicht durch ein Potential sondern durch
ein ausgetauschtes Teilchen beschrieben. Das ist bei relativistischen Teilchen sinnvoller, da
Teilchen relativistisch invariant beschrieben werden können. Ein Potential ist viel schwieriger
zu behandeln.
Für elektromagnetische Wechselwirkung ist das Austauschteilchen ein Photon, das Quant des
elektromagnetischen Feldes. Es gibt vier elementare Prozesse in der elektromagnetischen Wechselwirkung: die Emission oder Absorption eines Photons durch ein geladenes Teilchen sowie
die Erzeugung oder Vernichtung eines Teilchen-Antiteilchen-Paares. Keiner dieser in Abb.6.3
gezeigten Elementarprozesse kann als realer Vorgang mit freien geladenen Teilchen und Feldquanten auftreten, denn es ist nicht möglich, Energie- und Impulssatz gleichzeitig zu erfüllen.
e-
e-
γ
e-
e-
e-
γ
γ
e+
γ
e-
e+
Abbildung 6.3: Elementarprozesse der elektromagnetischen Wechselwirkung.
Die Lösung des Problems sieht folgendermaßen aus: die Erhaltungssätze von Energie und Impuls behalten ihre Gültigkeit in den elementaren Prozessen dadurch, daß mindestens eines der
Teilchen oder Quanten eines solchen Elementarprozesses virtuell ist, seine Masse unterscheidet
sich von der des realen (freien) Teilchens oder Feldquants (siehe obige Anmerkungen).
Betrachten wir als Beispiel die Paarvernichtung e− + e+ → γ in Abbidung 6.4b. Im Ruhesystem
des Paares ist der Impuls des Photons 0, seine Energie jedoch nicht: Eγ = Ee− +Ee+ ≥ 2me > 0.
Für ein reelles Photon mit Ruhmasse
p 0 muß pγ = Eγ sein. Das Photon ist in diesem Prozess
virtuell, seine Masse ist durch m̃ = Eγ2 − p2 > 0 gegeben1 .
Um nun die realen Prozesse der Quantenelektrodynamik zu behandeln kann man sich auf die
soeben dargestellten vier virtuellen Elementarprozessen beschränken. Wir betrachten die drei
Reaktionen, die in den Feynman-Diagrammen in Abbildung 6.4 dargestellt werden. Man kann
hier erkennen, wie sich die Prozesse aus den elementaren Graphen zusammensetzen.
a) e− + ‘p0 → e− + ‘p0
b) e+ + e− → µ+ + µ−
c) e+ e− → γ + γ.
1
Die Masse eines virtuellen Teilchens wird hier mit m̃ bezeichnet, um sie von der Masse m des realen Teilchens
zu unterscheiden.
124
Feynmandiagramme und Test der QED
µ
e
+
µ
p
γ
γ
virtuelles
γ
e
p
virtuelles γ
a)
e-
b)
e+
e-
c)
e+
Abbildung 6.4: Kombination der Elementarprozesse zu realen Prozessen: (a) Streugraph für die
Streuung eines Elektrons an einem ‘Diracproton’, d.h. an einem unrealistischen strukturlosen
Proton, (b) Vernichtungsgraph, (c) Graph mit virtuellem Elektron.
Es gibt eine eindeutige Zuordnung zwischen inneren Linien und virtuellen Teilchen sowie zwischen äußeren Linien und reellen Teilchen. In der Streureaktion (a) wird ein virtuelles Photon
ausgetauscht, dessen Massenquadrat negativ ist: m̃2γ = Eγ2 − p2γ < 0. Der Annihilationsgraph
(b) enthält ein virtuelles Photon mit positivem Massenquadrat m̃2γ = Eγ2 − p2γ = 4 E 2 > 0 (E
ist die Energie des Elektrons und des Positrons). Im dritten Graphen (c) gibt es ein virtuelles
Elektron. Die ein- oder auslaufenden Teilchen sind stets reell, die ausgetauschten Teilchen stets
virtuell.
Zusammengefaßt kann man die Feynman-Diagramme und -Regeln folgendermaßen beschreiben.
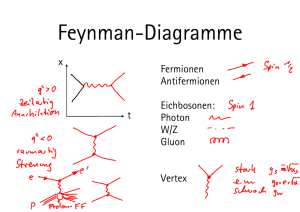
Liest man das Diagram von unten nach oben, so wird eine zeitliche Entwicklung einer Teilchenreaktion angedeutet: ein- und auslaufende Teilchen (Fermionen) werden mit Pfeilen in Bewegungsrichtung gekennzeichnet. Ein- und auslaufende Antiteilchen dagegen erhalten Pfeile entgegen ihrer physikalischen Bewegungsrichtung. Das ausgetauschte Teilchen dagegen verläuft quer.
Dies soll die zeitlich symmetrische Wechselwirkung von Emission-Absorption und AbsorptionEmission zweier Fermionen symbolisieren (mathematisch wird über beide Reaktionsrichtungen
summiert). Der Punkt, an dem Fermionen und Austauschteilchen miteinander koppeln wird
“Vertex” genannt. Hier nur ein paar Anmerkungen:
• Das ausgetauschte Teilchen ist virtuell. D.h. das Quadrat seines Vierervektors P ist:
P 2 6= m2 , während für ein reelles Teilchen gilt: P 2 = m2 .
• Die Kopplung des ausgetauschten Teilchens an die ein und auslaufenden Fermionen sind
charakteristisch für die Wechselwirkungsart: In der elektromagnetischen Wechselwirkung
ist sie durch die elektrische Ladung des Fermions gegeben, z.B. e für ein Elektron, 2/3 e
für u, c, t Quarks.
• Die einzelnen Elemente kann man dann in den mathematischen Ausdrücken für die
Streu- oder Zerfallsamplitude wiederfinden. Sie haben für jede Wechselwirkung eine andere
Struktur. Diese Amplituden werden wir in der Vorlesung E-Teilchen für Fortgeschrittene
ableiten2 .
Die Kopplung des ausgetauschten Teilchens an die ein und auslaufenden Fermionen ist charakteristisch für die Wechselwirkungsart ist. In der elektromagnetischen Wechselwirkung ist sie durch
2
Erinnerung: Das Quadrat der Amplitude geht in die Berechnung des Wirkungsquerschnitts oder der Zerfallsbreite ein.
6.3 Einige Reaktionen und Tests der QED
125
die elektrische Ladung des Fermions gegeben, z.B. e für ein Elektron. Das bedeutet bei einem
Ein-Photonenaustausch zwischen beispielsweise zwei Elektronen koppelt das virtuelle Photon
an jedem Knotenpunkt (Vertex) mit der “Kopplungsstärke” e. Dadurch entsteht insgesamt eine
Kopplung von α = e2 /4π = 1/137 (Feinstrukturkonstante). Bei einem Zwei-Photonenaustausch
verbinden insgesamt 2 virtuelle Photonen die Fermionen. Jeder Vertex enthält die “Kopplungsstärke” e wodurch eine Gesamtkopplung von α2 = (e2 /4π)2 ≈ 1/1372 . Prinzipiell kann
auf diese Weise die Wechselwirkungzwischen zwei Fermionen mit beliebig vielen Photonen als
Feynmandiagramm dargestellt werden. Allerdings ist der Wirkungsquerschnitt unter anderem
proportional zu α und (1/q 2 )2 , wobei q der relativistische Viererimpuls des Photons ist. Das
bedeutet, der Wirkungsquerschnitt für Zwei-Photonenaustausch ist um α ≈ 1/137 gegenüber
dem Ein-Photonenaustausch unterdrückt. Entsprechend verhält es sich für höhere Ordnungen
von α.
Abschließend sei folgende Aussage noch einmal verdeutlicht: An einem Vertex gelten alle Erhaltungssätze: Viererimpulserhaltung, Erhaltung der Leptonenzahlen, Baryonenzahl, usw.
Das Photon trägt weder Baryonenzahl noch Leptonenzahlen, folglich müssen alle Erhaltungsgrößen jeweils am Vertex erzeugt bzw vernichtet werden, wie aus Abbildung 6.4b) zu erkennen
ist.
6.3
Einige Reaktionen und Tests der QED
Im folgenden werden einige wichtige Reaktionen vorgestellt.
Elektron-Kern-Streuung. Das zugehörige Feynman-Diagramm niedrigster Ordnung ist ähnlich
wie in 6.4a) , wobei das Proton durch einen Atomkern der Ladung Ze ersetzt wird. Der differentielle Wirkungsquerschnitt ist durch die Rutherford-Formel gegeben
Z 2 α2
dσ
= 2 2 4
.
dΩ
4β p sin (θ/2)
(6.1)
(p Impuls, β Geschwindigkeit, θ Streuwinkel des Elektrons). In dieser Formel ist weder der
Spin des Elektrons noch des Atomkerns berücksichtigt. Die Formel ist nur eine Näherung für
genügend kleine Energien.
Myon-Paarerzeugung. Abbildung 6.4b) zeigt das zugehörige Feynman-Diagramm.√An den
Elektron-Positron-Speicherringen wird die Reaktion im Schwerpunktsystem gemessen. s = 2E
ist die Gesamtenergie. Der differentielle Wirkungsquerschnitt ist
dσ
α2
=
dΩ
4s
1 + cos2 θ .
(6.2)
Experimentelle Daten sind in Abb. 6.5 zu sehen. Die Winkelverteilung (1 + cos 2 θ) ist charakteristisch für Paarerzeugung von Spin 1/2-Teilchen und wird auch für τ + τ − - und Quark-AntiquarkPaare beobachtet. Integriert über alle Winkel folgt
4πα2
.
σµµ ≡ σ e− e+ → µ− µ+ =
3s
(6.3)
Der Wirkungsquerschnitt für e− e+ → µ− µ+ wird zur Normierung anderer Reaktionen benutzt,
insbesondere der Quark - Antiquark Produktion e− e+ → qq.
Elektron-Positron-Streuung/Annihilation Die Reaktion e− e+ → e− e+ wird Bhabha Streuung genannt und enthält im differentiellen Wirkungsquerschnitt drei Terme, von denen der erste
126
Feynmandiagramme und Test der QED
Abbildung 6.5: Die Reaktion e+ e− → µ+ µ− : Oben links Kinematik am Speicherring, rechts: der
gemessene differentielle Wirkungsquerschnitt (JADE-Detektor bei PETRA). Mitte: Der totale
Wirkungsquerschnitt als Funktion des Quadrats der Schwerpunktsenergie. Unten: Wie Mitte,
aber hier für die Produktion von τ + τ − Paaren.
6.3 Einige Reaktionen und Tests der QED
Abbildung 6.6: Differentielle Wirkungsquerschnitte für (a) Bhabha-Streuung (TASSO-Detektor
bei PETRA), (B) e+ e− → γγ (JADE-Detektor bei PETRA).
Abbildung 6.7: Integrierte Wirkungsquerschnitte für (a) Bhabha-Streuung (TASSO-Detektor
bei PETRA), (B) e+ e− → γγ (JADE-Detektor bei PETRA).
127
Feynmandiagramme und Test der QED
20
1000
OPAL
+ −
10
e e
40
OPAL
30
ee
γγ(γ)
cosθ* < 0.90
+ −
600
γγ(γ)
20
189 GeV
6
Events
dσ ⁄ dΩ [pb ⁄ sr]
σ [pb]
128
300
10
3
60
1
σ / σQED
100
0
1.2
1
0.6
30
0.8
0.3
0
0.2
0.4
0.6
0.8
1
cos(θ∗)
80
100
120
140
160
180
200
√s [GeV]
Abbildung 6.8: Differentieller Wirkungsquerschnitte für (a) e+ e− → γγ (OPAL Experiment bei
LEP), (B) Totaler Wirkungsquerschnitt für e+ e− → γγ.
vom Streugraphen, der zweite vom Vernichtungsgraphen und der dritte von der Interferenz der
beiden kommt.
dσ
α2 1 + cos4 (θ/2) 1 + cos2 θ 2 cos4 (θ/2)
(6.4)
+
=
−
dΩ
2s
2
sin4 (θ/2)
sin2 (θ/2)
Der erste Term kommt aus dem Streugraphen, der aussieht wie in Abb. 6.4a, wo das p durch
ein e+ ersetzt wird. Der zweite Term ist der Annihilationsgraph ( Abb. 6.4b, wo die Myonen
durch e− , e+ ersetzt sind) und der dritte gibt die Interferenz beider Amplituden wieder.
Die Daten in Abb. 6.6 stimmen sehr gut mit der Formel 6.4 überein und zeigen bei kleinen
Winkeln (θ → 0, cos θ → 1) ein starkes Anwachsen des Wirkungsquerschnitts, dσ/dΩ ∝
1/sin4 (θ/2).
Elektron-Positron-Annihilation in 2 Photonen Die Reaktion e− e+ → γγ ist im Feynmandiagramm 6.4c zu sehen. Sie hat eine interne Elektronlinie, einen Elektronpropagator, im
Gegensatz zu den bisher besprochenen Reaktionen. Diese Reaktion ist wichtig, weil selbst bei
den höchsten Energien Korrekturen aufgrund elektroschwacher Z  Interferenz klein sind. Der
differentielle Wirkungsquerschnitt ist gegeben durch:
dσ
α2 1 + cos2 θ
=
dΩ
s sin2 θ
Die Daten in Abb. 6.6 wurden am e+ e− Speicherring PETRA bei Schwerpunktsenergien
(6.5)
√
s<
∼ 44 GeV
6.3 Einige Reaktionen und Tests der QED
129
genommen und stimmen sehr gut mit der Formel 6.5 überein. Sie zeigen bei kleinen Winkeln (θ → 0, cos θ → 1) ein Anwachsen des Wirkungsquerschnitts. Für beide Reaktionen,
e− e+ → e− e+ und e− e+ → γγ, kann man über den gemessenen Winkelbereich integrieren und
− +
+ −
erhält dann die Resultate in Abb. 6.7. Die Messungen
√ > für e e → γγ wurden am e e Speicherring LEP bei höheren Schwerpunktsenergien s ∼ 90 GeV gemacht. Sie sind in Abb. 6.8 zu
sehen. Immer noch wird die QED bestätigt.
6.3.1
Feynmanregeln und Berechnung von σ (e+ e− → µ+ µ− )
Die Berechnung eines Wirkungsquerschnitts erfolgt i.a. über Fermis Goldene Regel (Gl. 2.8):
Übergangsrate w =
2π
|M|2 × ρ(E)
h̄
Die Feynmandiagramme liefern eine Methode, das Übergangsmatrixelement M zu berechnen.
Eines der wichtigsten Prinzipien beim Berechnen der Übergangsamplitude Mif mit Hilfe der
Feynmandiagramme ist die Faktorisierung, d.h. daß jeder Teil eines Diagramms einen Faktor
beisteuert.
Mif ist ein Produkt aus folgenden Faktoren:
a) Beiträgen der ‘äußeren Linien’ d.h. der ein- und auslaufenden Teilchen;
b) Vertexfaktoren, die die Punkte beschreiben, wo die Photonen an die Teilchen koppeln. In
der QED ist die Kopplung durch die elektrische Ladung des Teilchens gegeben, also e fürs
Elektron und z.B. 32 e fürs u-Quark. Meist drückt man e durch die Feinstrukturkonstante
α = e2 /4π aus.
c) Propagatoren, die die virtuellen Teilchen beschreiben. Der Propagator des Photons ist
∼ q12 , wobei q der Vierervektor des Photons ist.
Wir können jetzt das Matrixelement für e+ e− → µ+ µ− bis auf die Beiträge der äußeren Linien,
Elektronen und Myonen, und abgesehen von konstanten Faktoren aufschreiben:
Me+ e− →µ+ µ− ∼
√
α
1 √
α
q2
In Fermis Goldene Regel geht das Quadrat ein:
|Me+ e− →µ+ µ− |2 ∼
α2
q4
Für die Reaktion e+ e− → µ+ µ− ist der Viererimpuls des ausgetauschten Photons:
q = P + + P−
q 2 = s = (P+ + P− )2
P+ und P− sind die Vierervektoren von e− und e+ .
Um nach Fermis Goldener Regel den Wirkungsquerschnitt zu berechnen, brauchen wir noch
den Phasenraumfaktor
dn
ρ(E) ∼
dE0
130
Feynmandiagramme und Test der QED
√
wo E0 = s die Gesamtenergie ist. ρ ist die Dichte der Zustände. Wir bestimmen diese für ein
Teilchen im Endzustand, da der Impuls des zweiten nach Betrag und Richtung festliegt, wenn
der erste bekannt ist.
V p2 dp d(cosθ)dφ
V d3 p
=
dn =
h3
(2πh̄)3
p ist der Betrag des Myonimpulses im Endzustand, θ√und Φ sind Polar- und Azimutalwinkel.
Uns interessiert hier nur die Abhängigkeit von W = s.
Da p ≈ W2 ist bei hohen Energien, gilt: dp ∼ dW , und daher:
dn
∼ W2 ∼ s
dW
Damit wird die Übergangsrate nach Fermis Goldener Regel:
w ∼ |Me+ e− →µ+ µ− |2 · ρ
dn
σ ∼ |Me+ e− →µ+ µ− |2 ·
dW
α2
α2
∼ 2 ·s∼
s
s
Wir haben mit unserer einfachen Abschätzung die wesentlichen Faktoren erhalten. Der richtige
Ausdruck ist:
4πα2
+
−
+
−
σe e →µ µ − =
3s
6.3.2 Der Bosonpropagator
Der Propagator ist der Faktor, der virtuelle Teilchen im Matrixelement beschreibt. Vernachlässigt
man den Spin der Austauschteilchen, so kann man einen brauchbaren Ausdruck für den Propagator bei Benutzung des Yukawapotentials (Gleichung 1.14) bekommen. Das Yukawapotential
wurde für Austauschteilchen mit Masse M abgeleitet:
V (r) = −
g e−r/R
,
4π r
(6.6)
wobei R = 1/M die Reichweite und g die Kopplungsstärke g bedeutet. Das Yukawapotential
ist im Ortsraum definiert. Durch Fouriertransformation erhält man auf folgende Weise einen
Ausdruck im Impulsraum.
Sei das einlaufende und auslaufende Teilchen beschrieben durch:
~
ψi (~x) ∼ eiki ~x
~
ψf∗ (~x) ∼ e−ikf ~x
so gilt für die Übergangsamplitude:
Z
Z
∗
3
f (~q) = ψf (~x) V (~x) ψi (~x) d x = V (~x) ei q~ ~x d3 x
Dabei ist ~q = ~ki − ~kf der Dreierimpulsübertrag. Einsetzen des Yukawapotentials und Übergang
zu Polarkoordinaten liefert unter Benutzung von
~q ~x = q r cos θ
und
3
2
d x = r dr d(cos θ) dΦ
(6.7)
(6.8)
6.3 Einige Reaktionen und Tests der QED
f (~q) =
Integration ergibt:
Z
131
g e−r/R i q r cos θ 2
(−
)e
r dr d(cos θ) dΦ
4π r
f (~q) =
~q 2
g
+ M2
Dieser Ausdruck ist dem Propagator schon seh ähnlich. I.a. wird durch das Austauschteilchen
nicht nur Impuls, sondern auch Energie übertragen, dann setzt man statt q~2 den Viererimpulsübertrag q 2 ein.
Wichtige Grenzfälle sind die folgenden:
(fem (q 2 ) −−−
−→
2
M →0
2
gem
q2
Dies ist der Photonpropagator für elektromagnetische WW. gem ∼ e ∼
gnetische Kopplung, der Vertexfaktor.
2
fschwach (q ) −−
−−−→
2
2
2
gschwach
M2
|q |<<M
√
α ist die elektroma-
∼ GF
gilt für schwache Wechselwirkung, wobei GF ≈ 10−5 GeV−2 die aus β-Zerfällen bekannte schwache Fermi-Kopplungskonstante ist.
6.3.3
Test der QED: anomales magnetisches Moment des Myons
Der Feynmanformalismus wurde am Beispiel der elektromagnetischen Wechselwirkung entwickelt und erlaubt eine sehr präzise Berechnung von vielen Größen. Es gibt hochpräzise Tests
der Quantenelektrodynamik bei niedrigen Energien, z.B. Messung des Lambshift im Wasserstoffspektrum oder der magnetischen Momente von Elektron und Myon.
Insbesondere letzteres wurde gerade kürzlich mit wesentlich erhöhter Präzision in Brookhaven
(bei New York) gemessen. Man mißt an einem Myonspeicherring die Spinpräzession. Hier wird
ein kurzer Überblick gegeben.
Das Myon trägt – wie alle geladenen Fermionen –ein magnetisches Moment, welches für negative
Ladung entgegengesetzt zum Spin gerichtet ist:
µ
~ = g µB
~
S
h̄
µB = −
eh̄
2m
g ist der Landefaktor, der aufgrund von Experimenten (Stern-Gerlach, Zeeman, etc.) zunächst
auf g ' 2 gesetzt wurde. Aus der Diractheorie des Elektrons kommt ebenfalls g = 2 heraus. Korrekturen, die man im Rahmen der QED sehr präzise berechnen kann, führen zu einer
Abweichung, die folgendermaßen parametrisiert wird:
a=
~=
Da S
h̄
2
g−2
2
a+1=
g
2
~σ ist, hat die z-Komponente des magnetischen Moments den Wert:
µZ = g µ B ·
1
2
132
Feynmandiagramme und Test der QED
Im Magnetfeld führt der Spin eine Präzessionsbewegung aus. Für die Frequenz ωS leitet man
ab in Verallgemeinerung der klassisch abgeleiteten Frequenz der Larmorpräzession des magnetischen Moments, das mit dem Bahndrehimpuls korreliert ist:
ωS =
g eB
2 m
Relativistische Myonen, die auf einer Kreisbahn in einem Magnetfeld fliegen, haben die Zyklotronfrequenz
eB
.
ωZ =
γm
Für ein relativistisches Myon ist die Spinpräzessionsfrequenz unter Berücksichtigung einer Abweichung von g von 2:
1 eB
ωS = a +
γ
m
Falls also a = 0 ist, so ist ωS = ωZ . Da a aber von 0 abweicht, präzediert der Spin mit einer
etwas anderen Frequenz als der Umlauffrequenz. Das wird gemessen.
Das Resultat ist (2002):
aexp.
= 11659 177(7) 10−10
µ
athe.
= 11659 203(8) 10−10
µ
Die Zahl in Klammern gibt den Fehler an, der sich auf die letzte Stelle bezieht. Der Fehler
entspricht also weniger als 1 ppm (ppm=parts per million, d.h. 1 in 106 ).
Brookhaven Muon g-2 Data
200
a µ × 10
220
200
BNL’00
10
- 11659000
220
Standard Model
Prediction
World
Average
BNL’99
180
180
BNL’98
160
DH’98
160
Abbildung 6.9: Recent measurements of the anomalous magnetic moment of the muon (aµ ) in
Brookhaven compared with the currently best theoretical value (DH96).
6.3 Einige Reaktionen und Tests der QED
Es ist in Abb. 6.9 dargestellt. Man sieht, daß der experimentelle Wert um ca drei Standardabweichungen vom theoretischen abweicht. Solche Abweichungen könnten z.B. durch neue unbekannte
Teilchen hervorgerufen werden, die indirekt die gerechneten Korrekturen beeinflussen.
133
134
Feynmandiagramme und Test der QED
Kapitel 7
Quarks und Hadronen
7.1
Einleitung
Nachdem in den Jahren nach etwa 1950-60 immer bessere Hochenergiebeschleuniger zur Verfügung
standen und ebenso die Nachweistechniken verbessert wurden, wurde eine Vielzahl von teilweise sehr kurzlebigen (τ ∼ 10−24 s) Teilchen entdeckt. Es handelt sich um stark wechselwirkende
Mesonen und Baryonen. Man bezeichnet sie auch oft als “Resonanzen”, da man sie als resonanzartige Überhöhung im gemessenen Wirkungsquerschnitt sieht (beschrieben durch Breit-Wigner
Verteilungen, s. früher). Man war sich relativ bald klar, daß diese Teilchen nicht alle elementar
sind und suchte nach Ordnung in dem Wirrwarr.
Ein erster erfolgreicher Ansatz war die Klassifizierung nach Isospin, die wir in Kapitel 4 kennengelernt haben. Nach Auffinden der Seltsamkeit wurde ein erweitertes Schema durch Einführung
der “Hyperladung Y ” (Erinnerung Y = B + S, “Hyperladung ”, weil: Q = I3 + Y /2) probiert.
Dieses Schema war insofern folgenreich als es zur Einführung der Quarks führte.
Die Sprache, die hier benutzt wird, ist die der Gruppentheorie. Konnte man die Transformationen im Isospinraum als Mitglieder der Gruppe SU(2) auffassen, so haben wir es hier im
(Y, I3 )-Raum mit der Gruppe SU(3) zu tun. Wir wollen die Begriffe aus der abstrakten Gruppentheorie aber weitgehend vermeiden.
Später wurden dann weitere erhaltene Quantenzahlen gefunden, die im Quarkmodell jeweils
einem neuen Quark entsprachen: Charm und Bottom. Das Auffinden dieser Quarks war die
zweifelsfreie Bestätigung der Existenz von Quarks. Das alte Klassifizierungs-Schema mußte
daraufhin aber ungebührlich erweitert werden: SU(4) oder gar SU(5). Darauf werden wir nicht
eingehen.
7.2
Die Entdeckung der schweren Quarks
Im Jahr 1974 wurde innerhalb kurzer Zeit an zwei Labors ein Teilchen mit einer hohen Masse
von etwa 3.1 GeV/c2 entdeckt1 . Dieses Teilchen zerfiel hauptsächlich in Pionen, also über starke
Wechselwirkung. Es hatte für seine hohe Masse eine sensationell lange Lebensdauer: τ ∼ 10−20 s.
Die langlebigsten Hadronen hatten bis dato Lebensdauern von ∼ 10−23 − 10−24 s gezeigt.
Ein Entdecker des neuen Teilchens (S.C.C. Ting) nannte es J, der andere (B. Richter) nannte
es ψ. Heute heißt es J/ψ. Es ist das einzige Teilchen mit einem Doppelnamen. In Abb. 7.1 sind
die gemessenen Verteilungen der beiden Experimente zu sehen.
1
Die Bedeutung dieser Entdeckung für die Teilchenphysik kann man ahnen, wenn man hört, daß sie scherzhaft
oft die “Novemberrevolution der Teilchenphysik” genannt wird.
136
Quarks und Hadronen
Abbildung 7.1: Links: Invariante Masse der Zerfallsleptonen des J/ψ Teilchens, das in Brookhaven in einem Festtargetexperiment beobachtet wurde. Rechts: Dasselbe Teilchen, wie es in
e+ e− → Hadronen am SLAC (California) beobachtet wurde.
Abbildung 7.2: Beispiele für Messungen der niedrigsten Υ Resonanzen.
Was verhinderte den Zerfall mit der erwarteten Lebensdauer?
Nach kurzer Zeit intensiver Diskussionen und Messungen war klar, daß hier ein Teilchen, das
ein neues Quark enthielt, gefunden worden war, genauer ein Meson aus einem Quark c und
seinem Antiquark c. Hier steht c für Charmquark. 2
Zwei Jahre später wurde ein weiteres Teilchen entdeckt: das Ypsilon (Υ), welches als bb Zustand
interpretiert wurde, es enthält also ein weiteres neues schweres Quark, das bottom Quark b,
siehe Abb. 7.2. In diesen Zuständen, J/ψ und Υ, ist gleichzeitig das neue schwere Quark und
sein Antiteilchen enthalten. Man spricht von “verborgenem” charm oder “bottom”.
2
Das J/ψ Meson hat also keine neue Quantenzahl, obwohl es ein Charmquark enthält. Ein ähnlicher Fall
tritt auf beim Φ, welches aus ss besteht.
7.2 Die Entdeckung der schweren Quarks
Hauptquantenzahl
2S+1
n=1
n=1
n=2
n=2
n=2
n=2
n=2
n=2
1
S0
3
S1
1
S0
3
S1
3
P0
3
P1
3
P2
1
P1
LJ
137
JPC
cc Zustand
bb Zustand
0−+
1−−
0−+
1−−
0++
1++
2++
1+−
ηc (2980)
J/ψ(3097)
−
ψ(3686)
χc0 (3415)
χc1 (3511)
χc2 (3556)
−
−
Υ(9460)
−
Υ(10023)
χb0 (9860)
χb1 (9892)
χb2 (9913)
−
Tabelle 7.1: Vorhergesagte cc und bb Zustände mit Hauptquantenzahl n = 1 und 2. Die zugehörigen beobachteten Zustände mit Massen in MeV in Klammern.
Welche Zustände gibt es für ein System aus Quark/Antiquark? Da die c und b Quarks so schwer
sind, kann man sie nicht-relativistisch behandeln. Z.B. kann man Bahndrehimpuls und Spin
getrennt behandeln. In der Notation die wir aus der Quantenmechanik des Wasserstoffatoms
gewöhnt sind, lassen sich dann die Zustände in Tabelle 7.1 konstruieren. Die Paritäten und
C-Paritäten berechnen sich nach den Formeln aus Kapitel 4:
P = Pf f (−1)L = (−1)L+1
C = (−1)L+S
Hierbei ist Pf f die relative Parität von Fermion und Antifermion, Pf f = −1 (aus der Diracgleichung).
In e+ e− Wechselwirkung kann man leicht die Zustände erzeugen, die dieselben Quantenzahlen
haben wie das ausgetauschte Photon: J P C = 1−− . Dann koppelt das Photon resonanzartig an
den Zustand und im totalen Wirkungsquerschnitt sieht man eine starke Überhöhung bei der
Masse, s. folgende Skizze:
Das J/ψ und das ψ 0 , wie man den 2s Zustand ψ(3686) auch nennt, sind cc Zustände, die
die gleichen Quantenzahlen haben, wie das Photon. Warum sind sie so schmal, d.h. warum
haben sie eine so lange Lebensdauer? Das hängt mit den Zerfallsmöglichkeiten zusammen. Das
leichteste Meson, das nur ein Charmquark enthält, ist das D Meson (z.B. cd = D + , welches
eine Masse von 1.87 GeV hat). Hat man eine Mindestenergie von Ecms = 2 · mD zur Verfügung,
so kann ein System aus cc in 2 D Mesonen zerfallen. Man spricht von der Charmschwelle:
138
Quarks und Hadronen
Abbildung 7.3: Illustration der Zweig Regel. Quark Diagramm für den Zerfall eines Charmonium
Zustands in charmhaltige Mesonen. b) Zerfall in Mesonen ohne Charm.
2 · mD = 3.74 GeV
Nun ist mJ/ψ und auch mψ0 < 3.74 GeV, d.h. beide Mesonen können nicht unter Erhaltung
der Charmquarks gemäß Abb. 7.3a zerfallen. Eine Möglichkeit, hadronisch zu zerfallen, ist in
Abb.7.3b skizziert. Hier annihliert das cc Paar und Anfangs– und Endzustand sind unverbunden. Vor der Erklärung dieses Zerfalls in der QCD durch Gluonenaustausch (s. Ende dieses
Kapitels) wurde die Unterdrückung solcher Zerfälle als Regel formuliert3 :
Zweig Regel
Zerfälle, bei denen im Endzustand keine Quarks des Anfangszustands zu finden sind, sind unterdrückt.
Das System von cc lebt lange genug, daß man eine Anzahl von gebundenen Zuständen beobachten kann. Sie sind in Abbildung 7.4 dargestellt, ähnlich einem Termschema in der Atomphysik.
Viele dieser Zustände kann man erreichen durch radiative Übergänge, z.B.:
ψ 0 → χci + γ.
Die Quantenzahlen der χci , i = 1, 2, 3 sind in Tab.7.1 zu finden.
Das Niveauschema erinnert stark an andere Schemata, z.B. an das des Positroniums, eines gebundenen Systems aus e+ e− , s. Abb. 7.4. Das Positronium wird ausgebildet durch die elektromagnetische Wechselwirkung, deren Potential wohlbekannt ist. Bei den Quarkonium Systemen hat
man dagegen das Potential der starken Wechselwirkung zwischen Quarks, dessen Verlauf nicht
bekannt ist. Man kann es aber aus den beobachteten Niveaus von Charmonium und Bottomium
bestimmen. Man macht einen Ansatz, dessen r-Abhängigkeit zwischen dem Coulombpotential
mit ∼ r −1 und einem Oszillatorpotential ∼ r 2 liegt. Man erhält ein Potential, das bei kleinen
Abständen wie ∼ 1/r verläuft, während bei größeren Abständen ein Verlauf ∼ r gefunden wird:
a
V (r) = − + b r
r
(7.1)
Man kann die Schrödingergleichung benutzen, um (numerisch) aus den gemessenen Niveaus die
Konstanten a und b zu bestimmen:
a = 0.48
3
b = 0.18 GeV2
oft auch OZI Regel genannt, nach Okubo, Zweig, Ishikawa
7.2 Die Entdeckung der schweren Quarks
Abbildung 7.4: Links: Energieniveauschema für Charmonium, cc. Rechts: Energieniveauschema
für Positronium, e+ e− .
Abbildung 7.5: Links: Energieniveauschema für Bottomium, cc. Rechts: Potential der starken
Quarkwechselwirkung aus Anpassungen an Charmonium und Bottomiumdaten. Die durchgezogene Kurve hat die Form wie Gl. 7.1 und die gestrichelte wie 7.2
139
140
Quarks und Hadronen
paßt einigermaßen für das Charmonium und Bottomium Spektrum.
Die Form des Potentials ist nicht eindeutig bestimmt. Man erhält auch eine gute Beschreibung
der Beobachtungen mit der Form:
V (r) = a ln (b r),
a = 0.7 GeV und b = 0.5 GeV
(7.2)
Aber alle Potentiale, die die Spektren beschreiben, stimmen im Bereich 0.2 ≤ r ≤ 0.8 fm
überein, s. Abb. 7.5. Das heißt, das in diesem Bereich das Potential gut bestimmt ist.
Der Anstieg mit r hat einschneidende Konsequenzen. Entfernt man die Quarks voneinander, so
wächst das Potential zwischen ihnen rasch an. Rechnet man die Konstante b im Potential 7.1
mit Hilfe von h̄c um, so erhält man:
b = 0.18 GeV2 ≈ 1 GeV/fm ≈ 105 N.
Eine gewaltige Kraft! Man kann farbgeladene Teilchen wie z.B. die Quarks nicht voneinander
trennen. Diese Eigenschaft nennt man confinement, auf deutsch Einschluß.
7.3
Die leichten Hadronen
Das Quarkmodell war entwickelt worden, als es nur Hadronen gab, die die “leichten” Quarks
u, d, s enthalten. Nach der grandiosen Bestätigung der Ideen durch das Auffinden der Charmonium und Bottomium Spektren wurde dieses Modell auch für die leichten Teilchen ernst
genommen. Quantitativ kann man bei den leichten Quarks über die Quarkdynamik und das
Quarkpotential nicht allzu viel lernen, da es sich hier um relativistische Systeme handelt, die
schwierig zu behandeln sind.
Durch Analyse der bekannten Mesonen und Baryonen in einer Klassifikation nach Hyperladung und Isospin sind Gell-Mann und Zweig unabhängig voneinander auf das Quarkmodell
gekommen. Gell-Mann nannte sie “Quarks” (s. Einleitung), Zweig nannte sie “aces (=Asse)”.
Hyperladung hatten wir als Y = B + S kennengelernt, nach Auffinden der neuen Quarks mußte
man den Begriff verallgemeinern, man definiert: Y = B + S + C + B̃ + T . Dabei ist C die
Charmzahl, B̃, Bottomzahl und T Topzahl, s. Tabelle 7.2.
Quark
Masse
(GeV/c2 )
d
u
s
c
b
t
0.35
md
0.5
1.5
4.5
175
Q
−1/3
2/3
−1/3
2/3
−1/3
2/3
B
I3
S
C
B̃
T
Y
1/3
1/3
1/3
1/3
1/3
1/3
− 12
0
0
−1
0
0
0
0
0
0
1
0
0
0
0
0
0
−1
0
0
0
0
0
0
1
1/3
1/3
−2/3
4/3
−2/3
4/3
1
2
0
0
0
0
Tabelle 7.2: Ladung, ungefähre Massen und Flavour Quantenzahlen der Quarks. Die Bottomzahl
ist hier mit B̃ bezeichnet. Alle Zahlen folgen aus Y = B + S + C + B̃ + T und I3 = Q − Y /2.
Da wir es in diesem Abschnitt nur mit u, d, s zu tun haben, für die gilt C = B̃ = T = 0, ist
Y = B + S.
7.3 Die leichten Hadronen
7.3.1
141
Die leichten Mesonen
Die leichtesten Mesonen sind eine Familie von neun pseudoskalaren Mesonen mit J P =0− und
eine weitere Familie von neun Vektormesonen mit J P =1− Diese Teilchen sind experimentell
auch identifiziert worden. Die Familien kann man gut in sogenannten Gewichtsdiagrammen
darstellen, wo als Achsen I3 und Y gewählt werden. Für jedes vorhergesagte Teilchen, trägt
man einen Punkt ein, s. Tabelle 7.3.
¯ s̄ sind, gilt für die Parität, falls L=0
Für Mesonen aus Quarks ab, wo a = u, d, s und b̄ = ū, d,
ist:
P = Pab̄ (−1)L = (−1)L+1 = −1
Der Spin des Mesons ist dann gerade die Summe der Quarkspins, und kann daher 0 oder 1 sein.
Da es neun Kombinationen ab gibt, bekommt man gerade neun Zustände mit 0− und neun mit
1− wie experimentell beobachtet. Die pseudoskalaren Mesonen sind die K, π, η, η 0 Teilchen. Die
Vektormesonen sind K ∗ , ρ, ω, Φ.
In der Tabelle 7.5 sind die Teilchenkombinationen mit ihren Quantenzahlen zusammengestellt.
Meist sind die Zuordnungen zu den Punkten in den Gewichtsdiagrammen eindeutig außer in
¯ ss̄. Die wirklichen
der Mitte, wo es jeweils 3 Möglichkeiten gibt mit I3 = S = 0, nämlich uū, dd,
Teilchen entsprechen Mischungen (=Überlagerungen der Wellenfunktionen) für diese Zustände.
Man hat in der Mitte:
1
¯
√ (uū − dd)
2
1
¯
√ (uū + dd)
2
ss̄
I = 1, I3 = 0
(7.3)
I = 0, I3 = 0
(7.4)
I = 0, I3 = 0
(7.5)
Die Zuordnungen zu den I = 1, I3 = S = 0 Zuständen ist dann wieder eindeutig: π 0 mit Spin
0, und ρ0 mit Spin 1. Der Isospin 0 Zustand 7.4 und 7.5 mischt sich, es gibt als beobachtete
Zustände die skalaren Mesonen η, η 0 und die Vektormesonen ω und Φ. Das Φ mit einer Masse
von mehr als 1 GeV besteht praktisch nur aus ss.
Zeichnet man sich die Gewichtsdiagramme für die Quarks und Antiquarks, die in Tripletts angeordnet sind, so erhält man Tab. 7.6. Man sieht, daß die Mesonen durch einfache Superposition
(Addition von I3 und Y ) erhalten werden, die Baryonen durch Superposition von drei Quarks.
7.3.2
Die leichten Baryonen
Wir betrachten die leichten Baryonen, die nur aus u, d, s Quarks bestehen. Im Gegensatz zu
Mesonen, die in Nonetts vorkamen, gibt es bei Baryonen Oktetts, Singuletts und Dekupletts
(d.h. die Gewichtsdiagramme enthalten 8, 1, oder 10 Teilchen). Die Gewichtsdiagramme für die
+
+
leichtesten Baryonen sind in Tab. 7.4 dargestellt: es gibt ein J P = 12 Oktett und ein J P = 32
Dekuplett.
Im Oktett sind die Nukleonen mit S = 0 und die die Σ, Λ und die Ξ Teilchen (Ξ nennt
man auch “Kaskadenteilchen”) enthalten. Diese haben alle S = +1, sie zerfallen schwach mit
Lebensdauern von ∼ 10−10 s.
Das Dekuplett enthält stark zerfallende Resonanzen mit Lebensdauern ∼ 10−24 s bis auf das
Ω− , welches auch schwach zerfällt.
Diese Zustände folgen aus dem Quarkmodell, falls man annimmt, daß die totale Wellenfunktion
aus Raum und Spin Anteil symmetrisch ist gegen Vertauschung identischer Quarks. Das ist
142
Quarks und Hadronen
K
Y=S
1
6
0
π−
−1
K
+
+ I3
π1
π0 η
η0
−1
K−
K
ρ−
−1
K̄ 0
Y=S
1
6
∗0
K ∗+
+ I3
ρ1
ρ0 Φ
ω
−1
K ∗−
K̄ ∗0
Tabelle 7.3: Gewichtsdiagramme für das 0− und das 1− Mesonen Nonett.
∆
−
∆
Y=S+B
1
∆+
6
0
Σ∗−
−1
3
Σ∗+ I1
Σ∗0
−1
Ξ∗−
∆
++
n
Σ−
−1
Y=B+S
6
1
p
Σ-+ I3
1
Σ0 Λ
Ξ∗0
Ξ−
−1
Ξ0
Ω−
Tabelle 7.4: Gewichtsdiagramme für die Spin
3
2
und das Spin
1
2
Baryonen Multipletts.
7.3 Die leichten Hadronen
143
Quarkinhalt 0− Zustand 1− Zustand
I3
I
Y =S
us
K + (494)
K ∗+ (892)
1/2 1/2
1
0
∗0
ds
K (498)
K (896)
−1/2 1/2
1
.............................................................
ud
π + (140)
ρ+ (769)a
1
1
0
uu − dd
√
π 0 (135)
ρ0 (769)a
0
1
0
2
π − (140)
ρ− (769)a
−1
1
0
du
.............................................................
sd
K 0 (498)
K ∗0 (896)
1/2 1/2
−1
−
su
K (494)
K ∗− (892)
−1/2 1/2
−1
.............................................................
S. Text
η(547)
ω(782)
0
0
0
.............................................................
S. Text
η 0 (958)
φ(1019)
0
0
0
Tabelle 7.5: Quarkzusammensetzung und Quantenzahlen der Mesonen Nonetts.
Y=S+B
Y=S+B
1
1
6
6
s
d
u
I3
-
−1
1/2
−1/2
1
−1
−1/2
1/2
u
d
-
I3
1
s
−1
Tabelle 7.6: Gewichtsdiagramme für das Quark- und das Antiquark Triplett.
natürlich völlig unmöglich für Fermionen, da es dem Pauli Prinzip widerspricht. Die Lösung
wird sein, daß es noch eine weitere Eigenschaft gibt, die die Zustände dann antisymmetrisch
macht, nämlich die “Farbe” (s. Abschnitt 7.4).
Da Quarks Pq = 1 haben, hat ein Zustand aus drei Quarks mit L = 0 eine Parität P = Pa Pb Pc =
1.
Meist sind die Raumwellenfunktionen symmetrisch (L = 0), das wollen wir annehmen. Dann
müssen auch die Spinfunktionen symmetrisch sein. Symmetrische Spinfunktionen für Paare von
Fermionen bekommt man, wenn sie im S = 1 Zustand sind (S = 0 ist antisymmetrisch).
144
Quarks und Hadronen
D.h. für die 6 Kombinationen mit je 2 gleichen Quarks:
uud ddu ssd uus dds ssu
daß sie entweder Spin
1
2
oder
3
2
(7.6)
haben können (1 ± 21 ).
1 3
J =S= ,
2 2
Die 3 Kombinationen:
uuu, ddd, sss
(7.7)
müssen
3
2
haben, da nur dann alle Paare jeweils S = 1 haben.
Bleibt noch die Kombination uds. Hier kann man haben:
J =S=
Sud = 0
→
Sud = 1
→
1
2
1 3
S= ,
2 2
S=
(7.8)
(7.9)
Zählen wir jetzt die Zustände ab. Wir bekommen:
Für uud ddu ssd uus dds ssu 6 ×
Für uuu, ddd, sss
Für uds
2×
+
+
1+
2
1+
2
+
6 × 32
+
3 × 23
+
1 × 32
Also bekommen wir insgesamt 8 × 21 Zustände und 10 × 32 . Genau die Zustände hat man auch
gefunden, s. Tab. 7.4. Die Y und I3 Werte bekommt man aus denen der Quarks.
7.3.3
Massenaufspaltung der Baryonen Supermultipletts.
Betrachtet man die Massen der Baryonen in Tab. 7.7 und 7.8, so sieht man, daß innerhalb
eines Isospinmultipletts die Massen fast gleich sind. Größere Unterschiede sieht man bei den
Mitgliedern mit unterschiedlichem Y . Dieser Unterschied wird im Quarkmodell auf die Masse
des s Quarks zurückgeführt, welches schwerer ist als das u und d Quark. Daher kann man aus
den Massenunterschieden der Baryonen die Masse des s Quarks abschätzen.
MΩ − MΞ = MΞ − MΣ = MΣ − M∆ = ms − mu,d
MΞ − MΣ = MΞ − MΛ = MΛ − MN = ms − mu,d
Man bekommt also 6 unabhängige Schätzungen für die Differenz der s und u, d Quark Massen.
Mittelt man diese, so erhält man:
ms − mu,d ' 160 MeV.
Aus der Analyse der magnetischen Momente erhält man weitere Bedingungen für die Quarkmassen (s. Übung). Es ergibt sich:
ms ' 500 MeV
mu,d = 340 MeV.
7.3 Die leichten Hadronen
145
Quark Zustand
Inhalt
I3
I
S
uuu
∆++ (1232)a
3/2 3/2
0
+
a
uud
∆ (1232)
1/2 3/2
0
0
a
udd
∆ (1232)
−1/2 3/2
0
ddd
∆− (1232)a
−3/2 3/2
0
......................................
uus
Σ+ (1383)
1
1 −1
0
uds
Σ (1384)
0
1 −1
−
dds
Σ (1387)
−1
1 −1
......................................
uss
Ξ0 (1532)
1/2 1/2 −2
dss
Ξ− (1535)
−1/2 1/2 −2
......................................
sss
Ω− (1672)
0
0 −3
Tabelle 7.7: Leichte Baryonen mit L = 0: das
3+
2
Dekuplett.
Quark Zustand
Inhalt
I3
I
S
uud
p(938)
1/2 1/2
0
udd
n(940)
−1/2 1/2
0
....................................
uds
Λ(1116)a
0
0 −1
....................................
uus
Σ+ (1189)
1
1 −1
0
a
uds
Σ (1193)
0
1 −1
dds
Σ− (1197)
−1
1 −1
....................................
uss
Ξ0 (1315)
1/2 1/2 −2
dss
Ξ− (1321) −1/2 1/2 −2
Tabelle 7.8: Leichte Baryonen mit L = 0: das
1+
2
Oktett.
146
Quarks und Hadronen
Teilchen
Vorhersage (µN )
p(938)
2.79
n(940)
−1.86
Λ(1116)
−0.61
Σ+ (1189)
2.69
−
Σ (1197)
−1.04
Ξ0 (1315)
−1.44
−
Ξ (1321)
−0.51
7.4
Experiment (µN )
2.793
−1.913
−0.613 ± 0.004
2.458 ± 0.010
−1.160 ± 0.025
−1.250 ± 0.014
−0.651 ± 0.003
Farbe
Das Quarkmodell wie bisher besprochen, ist sehr erfolgreich, wenn auch für Baryonen scheinbar
im Widerspruch zum Pauli Prinzip. Dieses verlangt, daß die Wellenfunktion eines Zustandes bei
der Vertauschung zweier beliebiger identischer Spin- 12 Fermionen antisymmetrisch sein muß –
eine der grundlegenden Annahmen in der Quantenmechanik. Bei der Diskussion der leichtesten
Baryonen gingen wir aber von einer symmetrischen Raum– und Spinwellenfunktionen aus.
Diese Annahme ist für die Erklärung der beobachteten Baryonen entscheidend. Ginge man
dagegen von antisymmetrischen Funktionen aus, so würde man ein ganz anderes Spektrum
bekommen, welches mit dem Experiment nicht kompatibel ist (s. Übung). Das gleiche gilt für
die angeregten Zustände von Baryonen, die ebenfalls gut vom Quarkmodell erklärt werden,
vorausgesetzt, kombinierte Raum– und Spinwellenfunktionen sind symmetrisch.
Der eklatante Widerspruch zwischen Quarkmodell und Pauli Prinzip wurde 1964 von Greenberg aufgelöst. Er postulierte, daß Quarks außer Raum– und Spinfreiheitsgraden noch eine
weitere Eigenschaft aufweisen müssen, die er “colour” (Farbe) nannte. Die totale Wellenfunktion wird dann als das Produkt eines Raumteils ψ(~x) verstanden, eines Spinteils χ und einer
Farbwellenfunktion χc ; d.h.
Ψ = ψ(~x) χ χc .
Die Farbwellenfunktion wird weiter unten diskutiert. Das Pauli Prinzip muß somit für die totale Wellenfunktion angewendet werden, einschließlich des Farbteils χc . Konstruiert man eine
antisymmetrische Farbwellenfunktion, so können die kombinierten Raum– und Spinwellenfunktionen symmetrisch sein.
Den Farbwellenfunktionen werden erhaltene Quantenzahlen, “colour charges” =Farbladungen
zugeordnet. Sie spielen bei starken Wechselwirkungen eine ähnliche Rolle wie elektrische Ladung bei elektromagnetischen Wechselwirkungen. Dies wird im nächsten Abschnitt diskutiert.
Hier werden wir Farbladungen und Wellenfunktionen vorstellen und die Hypothese von Farb–
Confinement untersuchen.
Die Hypothese des Farb–Confinement besagt, daß Hadronen nur in sogenannten “colour singlet”
(Farbsinglett) Zuständen existieren können, für welche der Wert aller Farbladungen verschwindet.
Quarks dagegen, für die das nicht der Fall ist, können nur in Hadronen eingeschlossen existieren.
Dies erklärt auch den experimentellen Befund, daß Hadronen ganzzahlige elektrische Ladungen
haben, während gebrochen geladene Kombinationen wie qq und qqq, nicht zulässig sind.
7.4 Farbe
147
r
g
b
(a) Quarks
I3c
1/2
−1/2
0
Yc
1/3 r
1/3 g
−2/3 b
(b) Antiquarks
I3c
−1/2
1/2
0
Yc
−1/3
−1/3
2/3
Tabelle 7.9: Farbladung der Quarks und Antiquarks
7.4.1
Farbladungen und Confinement
(Wird in Vorlesung weggelassen)
Die Grundannahme der Farbtheorie ist, daß jedes Quark q = u, d, s, . . . in drei verschiedenen
Farbzuständen existieren kann: χc = r, g, b, was ‘rot’, ‘grün’ und ‘blau’ bedeutet. Ebenso wie
die Spinzustände χ = α, β den unterschiedlichen Werten der Spinkomponente Sz entsprechen,
entsprechen die Farbzustände χc den unterschiedlichen Werten der zwei Farbladungen, die als
“colour hypercharge”4 (Farbhyperladung) und “colour isospin charge” (Farbisospinladung) bezeichnet werden. Sie werden Y c und I3c genannt und ihre Werte für die Zustände χc = r, g, b
sind in Tabelle 7.9 aufgeführt.
Es handelt sich bei I3c und Y c um additive Quantenzahlen wie bei der elektrische Ladung.
Die Werte für zusammengesetzte Zustände aus Quarks und Antiquarks bekommt man daher
durch Addition. Somit wird ein Quark q im r–Zustand unter Ladungskonjugation in ein Quark
q im Farbzustand χc = r mit umgekehrten Werten Y c und I3c verwandelt, wie in Tabelle 7.9
angegeben.
Der experimentelle Nachweis der drei Farbzustände von Quarks wird demnächst besprochen.
Dort werden wir auch die physikalische Interpretation von Farbladungen als Ursprung der starken Wechselwirkung diskutieren (die Theorie, die das beinhaltet, ist die QCD (=Quantenchromodynamik). Hier diskutieren wir die Konsequenzen der Annahme, daß jedes Hadron, welches
als freies Teilchen existiert, die verschwindenden Farbladungen I3c = Y c = 0 haben muß.
Zunächst betrachten wir Baryonen, von denen man annimmt, daß sie aus drei Quarks von
geeignetem Flavour bestehen. Aus Tabelle 7.9 wird deutlich, daß sich die Farbladungen der drei
Quarks nur dann zu I3c = Y c = 0 addieren, wenn sich Baryonen aus einem r, einem g und
einem b Quark zusammensetzen. Diese Beobachtung führte zu dem Begriff “colour” (Farbe),
weil nach der Theorie der Farblehre weißes (d.h. farbloses) Licht durch die Kombination von
drei Primärfarben entsteht, z.B. rot, grün und blau5 . Die allgemeinste Farbwellenfunktion eines
Baryons ist demnach eine lineare Superposition von den sechs möglichen Permutationen; d.h.
χC
B = α1 |r1 g2 b3 i + α2 |g1 r2 b3 i + α3 |b1 r2 g3 i + α4 |b1 g2 r3 i + α5 |g1 b2 r3 i + α6 |r1 b2 g3 i,
(7.10)
wo zum Beispiel r3 bedeutet, daß das dritte Quark in einem r–Zustand ist und die αi (i =
1, 2, . . . , 6) Konstanten sind. Wenn wir die total antisymmetrische Kombination wählen:
1
χC
B = √ (|r1 g2 b3 − g1 r2 b3 + b1 r2 g3 − b1 g2 r3 + g1 b2 r3 − r1 b2 g3 i)
6
4
(7.11)
Die Bezeichnungen ergeben sich aus formalen Ähnlichkeiten mit der “normalen” Hyperladung und dem
Isospin bezogen auf Flavour.
5
Dies ist natürlich eine Analogie, denn die Quarkfarben haben absolut nichts mit normalen Farben zu tun!
148
Quarks und Hadronen
so können wir das Pauli Prinzip erfüllen mit einer symmetrischen Raum– und Spin Wellenfunktion wie in unserer früheren Diskussion über Baryonen angenommen. Man kann tatsächlich
zeigen, daß Farb–Confinement die Wahl 7.11 nicht nur zuläßt, sondern verlangt. Das erfordert
allerdings eine ausführlichere Betrachtung6 .
Nun betrachten wir die Kombinationen q m q n von m Quarks und n Antiquarks, welche durch die
Confinement Bedingung zugelassen werden. Es genügt, Kombinationen mit Baryonzahl B ≥ 0
zu berücksichtigen und somit m ≥ n, weil Teilchen mit B < 0 nur Antiteilchen von solchen mit
B > 0 sind. Die entsprechenden Farbwellenfunktionen können wie folgt beschrieben werden:
r α g β bγ r α g β b γ
(7.12)
wobei r α bedeutet, daß es α Quarks im r–Zustand etc. gibt7 und
m = α + β + γ > n = α + β + γ.
(7.13)
Wir erhalten die Farbhyperladung Y C und den Farbisospin I3C für die Farbwellenfunktion 7.12,
indem wir die in Tabelle 7.9 aufgeführten Farbladungen addieren. Mit der Confinement Bedingung, ergibt sich
α−α β−β
−
=0
2
2
(7.14)
α − α β − β 2(γ − γ)
+
−
= 0.
3
3
3
(7.15)
I3C =
und
YC =
Aus 7.14 und 7.15 folgt:
α−α =β−β =γ−γ ≡p
und mit 7.13
m − n = 3p,
wobei p eine nicht-negative ganze Zahl ist. Daher sind die einzigen vom Farb–Confinement
zugelassenen Kombinationen q m q n :
(3q)p (qq)n
(p, n ≥ 0),
wobei wir uns erinnern, daß wir uns auf Zustände mit Baryonzahl B ≥ 0 beschränkt haben.
Daraus folgt, daß Hadronen mit gebrochener elektrischer Ladung, wie
qq, qqq, qqqq, . . .
vom Farb–Confinement nicht zugelassen werden, während die Kombinationen qq und 3q, die im
einfachen Quarkmodell benutzt werden, zulässig sind. Kerne, die aus A Nukleonen bestehen und
somit 3A Quarks, sind ebenfalls Beispiele von Gleichung 7.13 mit p = A und n = 0, obwohl die
Quarkstruktur für die meist vernachlässigt werden kann. Ungewöhnlicher sind Kombinationen
wie
6
Der interessierte Leser findet sie in Abschnitt 6.3.2 von Martin+Shaw.
Es ist nicht nötig, die Anordnung der Faktoren zu berücksichtigen, da zum Beispiel rrb die gleichen Werte
von I3c und Y c aufweist wie rbr oder brr.
7
7.5 Gluonen
149
qqqq
und qqqqq.
welche exotische Mesonen bzw. Baryonen verursachen könnten. Es gibt trotz vieler Suchen
keinen überzeugenden Nachweis für derartige Zustände, und das einfache Quarkmodell gibt eine
gute Erklärung von Hadronen ohne sie. Trotzdem sind sie nicht unzulässig im Farb–Confinement
und können durchaus eine Rolle in der Hadronenphysik spielen. Zum Beispiel könnten Baryonen
im Prinzip kleine Anteile von qqqqq enthalten mit den gleichen erhaltenen Quantenzahlen wie
die dominierenden 3q Zustände, und solche Beimischungen könnten zum Teil verantwortlich
sein für die kleinen Diskrepanzen zwischen den gemessenen magnetischen Baryonmomenten
und denen, die vom einfachen Quarkmodell für Zustände mit L = 0 vorhergesagt werden.
7.5
Gluonen
Die elektrischen Kräfte zwischen geladenen Teilchen werden durch Photonen vermittelt. Da
es nur eine Sorte von Ladung (+) und Antiladung (−) gibt, existiert auch nur ein Typ von
Photon, das elektrisch neutral (ungeladen) ist. Die starken Kräfte zwischen Quarks werden
durch masselose Gluonen vermittelt. Diese Gluonen sind nicht neutral, sondern tragen selber
eine Farbladung in der Kombination Farbe-Antifarbe RG, RB, GR,. . . . Ein Beispiel für Gluonenaustausch zwischen Quarks ist in folgender Abbildung im Vergleich zu Photonaustausch
zwischen Ladungen dargestellt.
Es gibt drei Farben und drei Antifarben, also sollte man neun verschiedene Typen von Gluonen erwarten. Nur acht davon sind in der QCD vorhanden. Das neunte hat eine vollkommen
symmetrische Farb-Wellenfunktion
1
g9 = √ RR + BB + GG
3
(7.16)
und würde Kernkräfte unendlicher Reichweite zwischen den farbneutralen Hadronen vermitteln.
Daher muss es aus physikalischen Gründen ausgeschlossen werden8 . Die Tatsache, daß Gluonen
selbst Farbladung tragen, hat eine wichtige Konsequenz: Gluonen können – außer an Quarks –
auch an Gluonen koppeln. In folgender Abbildung sieht man Beispiele für erlaubte Möglichkeiten
der Kopplung von Gluonen an Gluonen.
8
Mathematisch geschieht das durch Wahl der SU(3)-Gruppe als Symmetriegruppe der Farbtransformationen.
Die acht Gluonen bilden ein Oktett der Farb-SU(3)-Gruppe.
150
Quarks und Hadronen
Hadronen als farbneutrale Systeme Eine befriedigende Theorie der Quark-Bindung in
Hadronen existiert noch nicht, wir beschränken uns daher auf einige intuitive Argumente. Man
kann in Analogie zu der Situation bei geladenen Teilchen plausibel machen, daß zwei Quarks
gleicher Farbladung sich abstoßen, Quark und Antiquark sich hingegen anziehen. Bei DreiQuark-Zuständen erhält man die festeste Bindung für total antisymmetrische Farbkombination,
z.B.
1
∆++ = √ (ur ug ub − ug ur ub + ug ub ur − ub ug ur + ub ur ug − ur ub ug ).
(7.17)
6
In Quark-Antiquark-Zuständen ergibt eine in den Farben symmetrische Kombination die festeste Bindung. Die Quarkdarstellung des positiven Pions lautet
1
π + = √ ur dr + ug dg + ub db
3
(7.18)
Man kann zeigen (und für das Meson ist es fast von selbst zu sehen), daß die acht Gluonen nicht an Drei-Quark-Zustände oder an Quark-Antiquark-Zustände ankoppeln (das neunte
Gluon würde dies tun und damit ein 1/r-Potential der Kernkraft hervorrufen). Diese Zustände
sind also farbneutral (“weiß”), so wie ein H-Atom elektrisch neutral ist. Die Farbneutralität
der beobachteten Hadronen ist eine Grundannahme der QCD. Es gibt deswegen keine direkten starken Kräfte zwischen Hadronen, ebensowenig wie es direkte Coulomb-Kräfte zwischen
neutralen Atomen oder Molekülen gibt.
Was ist nun aber die Natur der Kernkräfte, also der Kräfte zwischen den Nukleonen im Kern?
Auch hier hilft die Analogie zum elektrischen Fall. Die neutralen Moleküle in einem Öl üben
kurzreichweitige Kräfte aufeinander aus, die van-der-Waals-Kräfte, die auf induzierte Dipolmomente zurückzuführen sind. Die Kernkräfte sind wahrscheinlich die Van-der-Waals-Kräfte
der wirklichen starken Kräfte. Dies wuerde ihre kurze Reichweite erklären. Die starken Kräfte
wirken nur zwischen den farbgeladenen Quarks (bzw. Antiquarks).
Experimentelle Evidenz für die drei Farbzustände Es gibt mehrere experimentelle Resultate, die belegen, dass jeder Quark-Typ dreifach auftritt:
a) Die Hadron-Erzeugung in der Elektron-Positron-Vernichtung verläuft in weiten Energiebereichen vorwiegend über die Erzeugung von Quark-Antiquark-Paaren e− e+ → qq. Gemessene und berechnete Wirkungsquerschnitte stimmen nur dann überein, wenn man
jeden Quarktyp u, d, s, c, b, dreifach zählt. (s. unten)
7.5 Gluonen
151
b) Die Zerfallsbreite des π 0 -Mesons kann im Quarkmodell berechnet werden:
0.86eV für Nc = 1
0
Γ(π → γγ) =
7.75eV für Nc = 3.
Dabei ist Nc Anzahl der Farbladungszustände jedes Quarks. Die experimentelle Breite
von (7.74 ± 0.55) eV ist konsistent mit Nc =3.
c) Das τ -Lepton kann folgendermaßen zerfallen
 −
 e νe
−
µ− ν µ .
τ → ντ +

du
Für Nc =1 ist die Wahrscheinlichkeit etwa 33% für jeden Zerfallskanal. Für Nc =3 muss man den
hadronischen Zerfall dreifach wichten, und die Wahrscheinlichkeit für den e− ν e -Kanal beträgt
etwa 20%, was mit dem experimentellen Wert von (17.89 ± 0.14)% gut übereinstimmt, sofern
man Korrekturen auf die Lepton- und Quarkmassen vornimmt. Eine ähnliche Betrachtung
ergibt sich bei den Zerfällen der W- und Z-Bosonen.
7.5.1
e+ e− →Hadronen
Im Kapitel über Feynmangraphen hatten wir bereits den Prozeß e+ e− → µ+ µ− kennengelernt.
Er spielt eine besondere Rolle, da es der einfachste Prozeß ist, der in e+ e− Annihilation stattfindet, nur ein Diagramm trägt in niedrigster Ordnung bei (Erinnerung: bei Bhabha Streuung
e+ e− →e+ e− tragen zwei Diagramme bei). Der totale Wirkungsquerschnitt ist:
σµµ ≡ σ(e+ e− → µ+ µ− ) =
4πα2
3s
(7.19)
Der Prozeß e+ e− →Hadronen läuft außerhalb der Resonanzen in zwei “Stufen” ab: zunächst
e+ e− → qq, dann hadronisieren die Quarks, d.h. die farbgeladenen Quarks verwandeln sich in
farbneutrale Hadronen. Haben die Quarks genügend hohe Energie, so sind die entstehenden
Hadronen als Bündel von Teilchen im Detektor zu beobachten: Jets, s. Skizze und Abb. 7.6:
Man kann die Richtung der Jets rekonstruieren und ihren Polarwinkel θ relativ zur Achse der
e+ e− Strahlen auftragen. Die Verteilung ist in Abb. 7.7 zu sehen. Sie folgt einer 1 + cos2 θ
Abhängigkeit wie schon die für e+ e− → µ+ µ− , s. früher.
Da die Quarks drittelzahlige Ladungen haben, gilt z.B. für u Quarks:
2
σ(e− e+ → uu) = Nc · ( )2 · σµµ
3
(7.20)
152
Quarks und Hadronen
Abbildung 7.6: Zwei Jet Ereignis aufgenommen am e+ e− Speicherring PETRA.
Abbildung 7.7: Polarwinkelverteilung der Jets in 2 Jet Ereignissen.
und für d Quarks:
1
σ(e− e+ → dd) = Nc · (− )2 · σµµ
(7.21)
3
In weiten Energiebereichen läuft die Reaktion e− e+ → Hadronen vorwiegend über QuarkAntiquark-Paarbildung ab. Gleichung 7.19 kann zur Berechnung des Wirkungsquerschnitts benutzt werden. Das Verhältnis R des hadronischen und des Myon-Wirkungsquerschnitts ist
X
σ(e+ e− → Hadronen)
=
N
Q2q .
(7.22)
R≡
c
σ(e+ e− → µ− µ+ )
q
Hierin bedeuten Nc = 3 die Zahl der Farbzustände der Quarks und Qq · e die Quarkladung. Die
Summe √
ist über alle Quark-Sorten zu erstrecken, für deren Paarerzeugung die Schwerpunktsenergie s ausreicht. Die experimentellen Daten (Abb. 7.8) zeigen sehr schön den Faktor 3, der
die Farbladung der Quarks berücksichtigt.
7.5 Gluonen
153
Abbildung 7.8: Das Verhältnis R des Wirkungsquerschnitts für e+ e− →Hadronen zu dem für
e+ e− → µ+ µ− . Die durchgezogene Linie zeigt die Stufen, die der Erzeugung von schwereren
Quarks entsprechen. Gestrichelt eingezeichnet ist der erwartete Wert für Quarks ohne Farbe.
7.5.2
Hadronisierung
Der Prozeß der Hadronisation ist nur “im Prinzip” verstanden. Er ist nur zum Teil zu berechnen.
Er wird in der Praxis durch Simulationsrechnungen beschrieben. In Abb. 7.9 ist der Hadronisationsprozeß schematisch dargestellt. Das farbgeladene Quark und Antiquark-Paar, welches durch
die e+ e− Wechselwirkung entstanden ist, baut beim Auseinanderfliegen ein Farbfeld zwischen
sich auf. Da das Farbladungspotential von der Form:
V (r) = −
4 αs
+ f0 r
3r
ist, wächst die potentielle Energie zwischen den Quarks dabei an. Bei genügend hoher Energie
ist es energetisch günstiger, daß sich weitere Quark-Antiquark Paare bilden, die Endpunkte kürzerer Farbfeldlinien sind. Dieser Prozeß geht kaskadenartig weiter, bis zu einer unteren
Energiegrenze. Die dabei entstandenen Quark Antiquark-Paare bilden in einem letzten Schritt
farbneutrale Mesonen, die zerfallen, bis nur noch stabile Teilchen übrig bleiben.
Selten bilden sich an den Enden der Farbfeldlinien Paare von Diquark und Anti-diquark und
es kommt zur Bildung von Baryonen.
7.5.3
Entdeckung der Gluonen
Der erste indirekte Hinweis auf die Existenz der Gluonen stammt von den Experimenten zur tief
unelastischen Elektron-Nukleon-Streuung (nächstes Kapitel). Die gemessene Strukturfunktion
wurde zur Berechnung der Impulse der Partonen im Proton verwendet, mit dem überraschenden
Ergebnis, daß die geladenen Partonen, die Quarks, nur etwa 50% des Nukleon-Impulses tragen.
Also mußten im Nukleon auch noch ungeladene Partonen vorhanden sein, die wegen ihrer
elektrischen Neutralität keine Streuung der Elektronen bewirken können. Diese Objekte wurden
Gluonen genannt, weil man vermutete, dass es sich dabei um die Bindeteilchen der starken
Wechselwirkung handeln könnte.
154
Quarks und Hadronen
Abbildung 7.9: Schematische Darstellung der Hadronisation.
Abbildung 7.10: Links: Ein 3 Jet Ereignis aufgenommen im e+ e− Speicherring PETRA. Rechts:
Winkelverteilung für 3 Jet Ereignisse, durchgezogene Kurve für Spin 1 Gluonen, gestrichelte
für Spin 0 Gluonen.
Die direkte Entdeckung der Gluonen gelang im Jahr 1979 am Elektron-Positron-Speicherring
PETRA in Hamburg. Die grundlegende Idee der PETRA-Experimente war, nach Ereignissen
zu suchen, in denen die Quarks ein Feldquant über den Mechanismus der Gluon-Bremsstrahlung
emittieren. Für elektrisch geladene Teilchen, insbesondere Elektronen, ist dies wohlbekannt: der
Bremsstrahlungsprozess ist die physikalische Grundlage für die Erzeugung von Röntgenstrahlung
und hochenergetischer γ-Strahlung an Elektronenbeschleunigern. Auch bei Elektron-Positron-
7.6 Die “laufende” starke Kopplung αs
Reaktionen spielt die Abstrahlung eine Rolle.
Der entsprechende Prozess der starken Wechselwirkung sollte bei Quark-Antiquark-Endzuständen
beobachtbar sein
(7.23)
e− + e+ → q + q + gluon.
Wir wissen bereits, dass Quarks nicht direkt, sondern nur über ihre Hadron-Jets beobachtbar
sind, und dasselbe ist für das Gluon zu erwarten. Die Reaktion 7.23 sollte also zu Ereignissen
mit drei Hadron-Jets führen. Diese wurden erstmals im Jahr 1979 bei PETRA gefunden, zuerst
im TASSO-Experiment und wenig später in den Experimenten JADE, MARK J, PLUTO und
CELLO. Aus einer Analyse der Winkelverteilung zwischen den drei Jets kann man schließen,
dass die Feldquanten wie erwartet den Spin 1 haben (s. weiter unten).
Weitere Hinweise auf die Existenz von Gluonen ergeben sich aus den Zerfällen des Υ-Mesons.
Die neutralen Vektormesonen J/ψ = |cci und Υ = |bbi können nicht in ein Paar von D- bzw.
B-Mesonen zerfallen, da ihre Ruheenergie hierfür zu niedrig ist. Ein hadronischer Zerfall muss
über die Quanten der starken Wechselwirkung erfolgen. Die Vektormesonen J/ψ = |cci und
Υ = |bbi zerfallen in drei Gluonen, die Mesonen mit Spin 0 wie das ηc in zwei Gluonen. Die
geringe Breite der J/ψ- und Υ-Teilchen ist eine Konsequenz des Dreigluonzerfalls und kann
theoretisch berechnet werden.
Die Erzeugung und der Zerfall von Υ-Mesonen können am besten mit e+ e− -Speicherringen untersucht werden. Wegen der niedrigen Schwerpunktsenergie beobachtet man keine deutlichen
Drei-Jet-Ereignisse; vielmehr sind die Jets relativ breit und verschmelzen ineinander. Aus einer statistischen Analyse von vielen tausend Ereignissen konnte geschlossen werden, dass die
Hadron-Erzeugung bei der Resonanz über drei Gluonen abläuft, während neben der Resonanz
die Quark-Antiquark-Erzeugung dominiert.
√
e+ e− → Υ → 3 Jets für s = MΥ
√
e+ e− → qq → 2 Jets für s 6= MΥ
7.5.4
Spin des Gluons
Man kann trotz des confinements, also der Tatsache, daß man weder Quarks noch Gluonen frei
beobachten kann, viele Eigenschaften der Gluonen experimentell bestimmen. Sie hadronisieren
ähnlich wie Quarks und sind bei genügend hoher Energie als Jet im Detektor zu beobachten.
Hier wird als√Beispiel die Bestimmung des Gluonspins diskutiert. In e+ e− Annihilationsexperimenten bei s ∼ 30 GeV sucht man nach Ereignissen mit 3 Jets und ordnet sie der Energie
nach:
E1 > E 2 > E 3 .
Da das Gluon aus Bremsstrahlungsprozessen stammt, ist es mit großer Wahrscheinlichkeit der
Jet mit der niedrigsten Energie E3 .
Im Schwerpunktsystem von Jet 1 und 2 schaut man die Winkelverteilung des 3. Jets an, s.
Abb. 7.10. Trotz Verschmierung ist deutlich zu erkennen, daß die Daten besser mit der Spin 1
Hypothese übereinstimmen.
7.6
Die “laufende” starke Kopplung αs
Die Quantenchromodynamik (QCD) ist eine Theorie ähnlich wie die Quantenelektrodynamik,
die aber die starke Wechselwirkung zwischen Quarks beschreibt. Die Farbladung der Quarks
155
156
Quarks und Hadronen
ist Grundlage, die Austauschteilchen sind Gluonen, die selbst farbgeladen sind. Die Kopplung
der Gluonen an Quarks und auch der Gluonen untereinander, wird beschrieben durch den
Kopplungsparameter αs .
Die starke Kopplung αs ist uns begegnet beim Potential, das man aus Quarkoniumanalysen
extrahiert hat. Weiterhin hat man αs aus der 3 Jet Rate in e+ e− Annihilation extrahiert.
Dort wurde erstmals klar, daß αs eine Energieabhängigkeit hat. Diese Energieabhängigkeit von
Kopplungen ist typisch für alle Wechselwirkungen, die durch Feldtheorien beschrieben werden.
Sie wurde gemessen für die starke und die elektromagnetische Wechselwirkung. Vermutlich gilt
das auch für die schwache Wechselwirkung, wo der Effekt aber noch nicht gemessen wurde.
Abbildung 7.11: αs (Q2 ) bei den Werten ‘Q2 ’ der Messung. Die Messpunkte sind bei der Masse
des τ , des J/ψ, des Υ, aus tief-unelastischer Streuung, für e+ e− Ereignisraten bei 25 GeV,
Analysen der Ereignisform. Die höchsten Punkte stammen von LEP: Analyse der Breite des Z 0
und Analysen der Ereignisform. Die Kurven gibt die QCD Erwartung für Λ = 0.2 GeV wieder.
Am stärksten ist die Abhängigkeit bei der starken Wechselwirkung, dort wurde in der englischen Literatur auch der Ausdruck “running coupling constant” geprägt. Auf deutsch hat sich
7.6 Die “laufende” starke Kopplung αs
157
kein Ausdruck für αs wirklich eingebürgert, manchmal wird von dem “gleitenden” Parameter
gesprochen9 . Betrachten wir das Bild αs (Q2 ) als Funktion von Q2 (Abb. 7.11). Je nach Experiment muß für Q2 etwas anderes eingesetzt werden. In Abb. 7.11 ist zu sehen, daß αs bei kleinen
Q2 so groß wird, daß störungstheoretische Rechnungen nicht mehr sinnvoll ausgeführt werden
können. Der Bereich, wo αs sehr groß wird, ist der “confinement” Bereich, in dem die Quarks
so starke Kräfte erfahren, daß sie “gefangen” sind. Der andere Grenzfall ist der Bereich hoher
Energie, wo αs klein wird, so daß Störungsrechnungen möglich sind. Das ist der Bereich der
asymptotischen Freiheit: dort kann man die Quarks als fast freie Teilchen behandeln.
In niedrigster Ordnung Störungstheorie gilt:
αs (Q2 ) =
4π
(11 −
2
3
nf ) ln
Q2
Λ2
.
(7.24)
nf ist die Anzahl der beteiligten Quarkflavours (ohne die Farbe zu zählen!), also bei der Masse
des Z 0 , welche heutzutage meist als Referenz benutzt wird, ist nf = 5. Λ nennt man den
Skalenparameter der QCD, er muß experimentell bestimmt werden. Der heutige Wert ist Λ '
200 MeV/c.
√
Für den Parameter ‘Q’ setzt man bei e+ e− Annihilation in Jets Q = s, bei Analyse des Υ
oder τ Zerfalls setzt man die Υ- oder τ -Masse ein. Bei tiefunelastischer Streuung ep → eX
(HERA) setzt man den Viererimpulsübertrag Q2 = −q 2 = −(k − k 0 )2 ein, wobei k und k 0
die Viererimpulse des Elektrons vor und nach der Streuung sind. Nach der Unschärferelation
∆px ·∆x ∼ h̄ (in einer Dimension) entspricht einem Impulsübertrag ein “Abstand”. Man spricht
deshalb auch oft von der Abstandsabhängigkeit von αs . Also hat man confinement bei großen
Abständen, asymptotische Freiheit bei kleinen.
Die Abhängigkeit der Kopplung vom Abstand oder vom Impulsübertrag kann man sich anschaulich klar machen. Wir beginnen mit der elektromagnetischen Wechselwirkung. Bringen
wir eine Ladung q in ein polarisierbares Dielektrikum ein, so ist das elektrische Feld:
~ =
|E|
~ 0|
|E
q
=
4π0 r
~
0 ist die Dielektrizitätskonstante des Mediums. Das Medium wird polarisiert und das Feld |E|
ist kleiner als das Feld ohne Medium, da > 1. Man könnte alternativ auch davon ausgehen,
daß die Ladung q kleiner ist als ohne Medium q = q0 . Sie wird durch die polarisierten Moleküle
~ oder die Ladung q mit einer Sonde, so
des Dielektrikums abgeschirmt. Mißt man das Feld E
wird man eine Abstandsabhängigkeit feststellen.
Nun ist eine Ladung, die durchs Vakuum fliegt, ständig von Photonen umgeben, die emittiert
und wieder re-absorbiert werden (Abb. 7.12 links). Sie können manchmal ein virtuelles e+ e−
Paar bilden (Abb. 7.12 rechts). Diese Paare bauen wieder eine Polarisation auf, eine “Vakuumpolarisation”: die entgegengesetzten Ladungen sind im Mittel dichter beim Elektron als die
gleichnamigen. Mißt man seine Ladung mit einer Sonde als Funktion des Abstands, so wird die
Abschirmung geringer, je näher die Sonde herankommt.
Die Abhängigkeit der elektromagnetischen
ist in
√ Kopplungskonstanten vom Impulsübertrag
1
e+ e− Annihilation gemessen worden: bei s = MZ ≈ 92 GeV beträgt αem (MZ ) ≈ 128
anstatt
1
dem wohlbekannten αem (0) ≈ 137
bei kleinen Impulsüberträgen. Die Änderung ist etwa 7% (s.
Abb. 7.13).
9
Eigentlich ist das Wort ‘Konstante’ ja nicht mehr angebracht!
158
Quarks und Hadronen
Abbildung 7.12: Links: Emission und Re-absorption eines Photons durch ein Elektron (a). Der
zugehörige Austauschprozeß (b). Rechts: Das emittierte Photon bildet ein e+ e− Paar (a) und
der zugehörige Austauschprozeß (b).
α-1(Q)
155
150
TOPAZ µµ/eeµµ and qq average:
Fits to leptonic data from:
DORIS, PEP,
PETRA,
TRISTAN
145
140
α (0)
-1
135
αSM(Q)
-1
130
OPAL
125
120
115
110
105
OPAL 2-fermion fits:
average:
0 20 40 60 80 100 120 140 160 180 200
Q / GeV
−1
Abbildung 7.13: α√QED
aus Messungen in e+ e− Annihilation als Funktion der Schwerpunktenergie (hier ist Q = s).
Die Änderung der starken Kopplung αs mit dem Impulsübertrag µ ist wesentlich größer und sie
läuft in anderer Richtung. αem wird größer mit wachsendem Impulsübertrag, αs wird kleiner.
Bei αs kommt zusätzlich die Eigenschaft der Gluonen zum Tragen, die sie wesentlich von den
Photonen unterscheidet: Gluonen tragen Farbe (und Antifarbe). Man kann 8 Gluonen unterscheiden, z.B. kann man wählen:
gi = RB, RG, BR, BG, GB, GR,
(i = 1, . . . , 6)
und
1
g7 = √ (RR − GG)
2
und
1
g8 = √ (RR + GG − 2BB).
6
7.7 Nochmal: Zerfall des J/ψ
(Der symmetrische Zustand
√1
3
(RR + GG + BB) tritt nicht auf!)
Man kann ähnlich wie in der elektromagnetischen Wechselwirkung versuchen, das Verhalten von
αs mit dem Abstand “anschaulich” zu verstehen. Für die Diskussion hier ist nur wesentlich, daß
es Gluonen gibt, die die Farbe des Quarks ändern (g1 . . . g6 ) und solche, die das nicht tun (g7 und
g8 ). Bewegt sich ein Quark durch das Vakuum, so emittiert und reabsorbiert es Gluonen. Dabei
kann die Farbe des Quarks gleich bleiben oder sie ändert sich. Zu dem in Analogie zum oben
beschriebenen Mechanismus der QED qr → qr +g7 (z.B.) kommt folgender hinzu: qr → qg +RG.
Mißt man in letzterem Fall mit einer rot-sensitiven Sonde die Farbladung des Quarks, so wird
die Ladung geringer mit abnehmendem Abstand, da sich ja das qr in ein qg verwandelt hat.
Austauschdiagramme in Analogie zu Abb. 7.12 sind in der folgenden Abbildung zu sehen:
Welcher Mechanismus überwiegt, die Abschirmung wie in der QED oder die Ausbreitung der
Farbladung durch die Gluonen, ist nicht von vornherein klar: in der Praxis überwiegt bei jetzigen
Energien der zweite Anteil und es gibt eine “Antiabschirmung”, d.h. die Farbladung erscheint
kleiner mit abnehmendem Abstand Sonde-Quark. In Gleichung 7.24 sieht man, daß das formal
bis nf ∼ 16 der Fall ist.
Die Abhängigkeit vom Impulsübertrag folgt der Vorhersage der QCD mit einem Parameter Λ ≈
200 MeV.
7.7
Nochmal: Zerfall des J/ψ
Wir hatten oben gesehen, daß das J/ψ hadronisch zerfällt, der Zerfall in D D (s. Skizze unten
rechts) ist aber energetisch nicht möglich. Der Zerfall z.B. in 3 Pionen findet statt, ist aber nach
der Zweig Regel unterdrückt. In der QCD findet das die folgende Erklärung.
Die einzige Möglichkeit der J/ψ Mesonen, hadronisch zu zerfallen, ist über Annihilation in
ein System von Gluonen, Austauschteilchen der starken Wechselwirkung, die dann wiederum
leichte Mesonen bilden10 .
Wieviele Gluonen müssen ausgetauscht werden? Im Anfangs– und Endzustand hat man beobachtbare Hadronen, die immer farbneutral sind. Das System von Gluonen muss also auch
farbneutral sein, d.h. es müssen mindestens zwei Gluonen ausgetauscht werden. Zwei gehen
aber nicht wegen der C–Parität: das J/ψ hat C = −1, Gluonen auch (in Analogie zu Photonen). Daher haben zwei Gluonen C = +1. Also müssen drei oder mehr Gluonen ausgetauscht
werden, wie in der Skizze links:
10
Natürlich können die J/ψ und ψ 0 Mesonen auch elektromagnetisch oder auch schwach zerfallen. Solche
Zerfälle sind aber noch viel weniger wahrscheinlich als die Annihilation über Gluonen.
159
160
Quarks und Hadronen
Solche Prozesse höherer Ordnung sind aber unterdrückt. Das Matrixelement enthält 6 QuarkGluon Vertizes, die Zerfallsrate ist also ∝ αs6 .
Die Unterdrückung solcher Übergänge, bei denen die Quarks des Anfangszustandes nicht mehr
im Endzustand zu finden sind, wurde als “Zweig Regel” formuliert. Sie wurde lange vor der
QCD Erklärung gefunden.
Kapitel 8
Tiefunelastische Streuung: Struktur
des Nukleons
8.1
Einleitung
Die Streuung von Leptonen an Nukleonen ist besonders gut geeignet, um die Struktur der Nukleonen zu erforschen. Leptonen sind unserem Wissen nach strukturlos, ihre Wechselwirkungen
sind gut verstanden. Zudem können Leptonstrahlen mit hohen Energien und hoher Intensität
produziert werden.
In der Praxis sind die Leptonen e± , µ± und νµ , ν̄µ verwendet worden. Die geladenen Leptonen
wechselwirken bei nicht zu hohen Energien überwiegend elektromagnetisch während die Neutrinos natürlich ausschließlich schwach wechselwirken. Die Untersuchungen mit Neutrinos sind
daher zum Teil komplementär zu den mit geladenen Leptonen durchgeführten Untersuchungen.
Der Ansatz, durch Messung von Energie- und Streuwinkelverteilung des Leptons die Struktur des Nukleons zu untersuchen, hatte sich schon bei der Erforschung vergleichsweise großer
Strukturen als erfolgreich erwiesen.
Die Compton-Wellenlänge λC ∼ h/|Q| liefert dabei ein Maß für die Auflösung. Dabei ist |Q|
der Betrag des Viererimpulses des zwischen Lepton und Nukleon ausgetauschten Bosons. Der
maximal
mögliche Wert von |Q| (Energie und Impulserhaltung) ist durch die Schwerpunktener√
gie s gegeben. Höhere Schwerpunktenergie erlaubt also einen tieferen Einblick in das Innere
des Protons.
• Rutherford führte im Jahre 1911 ein Experiment durch, bei dem α-Teilchen an einer Gold
Folie gestreut wurde. Aus der Winkelverteilung konnte auf die Existenz der Atomkerne,
als Zentren konzentrierter Ladung geschlossen werden.
• In den 50er Jahren bestimmten Hofstadter und McAllister die Verteilung der elektrischen
Ladung in Atomkernen, indem sie Elektronen an Kernen streuten.
• Ein Durchbruch im Verständnis der Struktur der Nukleonen gelang 1968 am Stanford
Linear Accelerator Center (SLAC). Die Messungen am SLAC zeigten erstmals, daß Protonen aus Quarks, punktförmigen Teilchen mit Spin 1/2, zusammengesetzt sind. Dieses
Ergebnis war von entscheidender Bedeutung für die Entwicklung der QCD, der Feldtheorie
der starken Wechselwirkung.
• Die seit den 70er Jahren durchgeführten Experimente (e, µ, ν Streuung an Protonen,
162
Tiefunelastische Streuung: Struktur des Nukleons
Deuterium sowie schwereren Kerne) haben das Verständnis der Struktur der Nukleonen
und der QCD weiter präzisiert.
• Seit 1992 wird in Hamburg am DESY der Elektron Proton Speicherring HERA betrieben. Hier werden erstmals Elektronstrahlen (27.5 GeV) mit Protonstrahlen
(920 GeV) zur
√
Kollision gebracht. Die Schwerpunktsenergie bei HERA von s = 320 GeV entspricht einem ’Fixed Target’ Experiment mit einer Elektronstrahlenergie von etwa 50 TeV. Die
hohe HERA-Energie erlaubt die Erzeugung extrem hoher Impulsüberträge1 (maximal
Q2 = s ≈ 100000 GeV2 und damit einen viel tieferen Einblick in die Struktur der Nukleonen (λC ∼ 10−3 fm) als frühere Experimente (SLAC: 1/30 fm). Ziel ist nicht nur die
präzise Untersuchung der Protonstruktur, sondern auch die Suche nach einer möglichen
Substruktur von Quarks.
Abbildung 8.1: ‘Auflösung’, d.h. λC , die in verschiedenen Experimenten zur Streuung erreicht
wird.
Im folgenden wird zunächst die elastische Streuung an Nukleonen besprochen. Darauf aufbauend
wird danach unelastische Streuung erläutert.
8.2
Elastische Streuung
8.2.1
Elastische Streuung an Punktladungen
Strukturuntersuchungen mit Leptonen wurden zunächst in elastischen Reaktionen durchgeführt:
e+p → e+p
Das wichtige bei elastischer Streuung ist, daß das Targetteilchen, in diesem Falle also das Proton,
bestehen bleibt. Der Wirkungsquerschnitt kann exakt berechnet werden, falls man annimmt,
1
Es ist allgemein üblich als Einheit für Q2 GeV2 anzugeben statt (GeV/c)2 .
8.2 Elastische Streuung
163
daß das Proton, an dem die Streuung stattfindet, strukturlos ist. Berücksichtigt man den Spin
1
beider Teilchen, so lautet der Wirkungsquerschnitt in voller Allgemeinheit:
2
d σ Q2
θ
dσ
2 θ
(cos
=
+
sin2 )
2
dΩ
dΩ R
2 2M
2
2
α
d σ =
2
dΩ R
4 E sin4 θ2
(8.1)
(8.2)
Der Index “R” bezeichnet den Rutherfordquerschnitt. Er kann wie oben differentiell im Raumwinkel des gestreuten Elektrons ausgedrückt werden oder auch durch den Vierimpulsübertrag
Q2 . Definition der Variablen und kinematische Beziehungen sind in den Tabellen zu finden. Bei
der Berechnung wird zumeist die Elektronenmasse vernachlässigt. Der Wirkungsquerschnitt Gl.
(8.1) ist dann:
d σ θ
dσ
Q2
=
tan2 )
(8.3)
(1
+
2
2
2
dQ
d Q M ott
2M
2
Darin ist der Mott-Querschnitt enthalten, bei dem der Spin des Protons vernachlässigt wird:
4πα2 E 0 2 θ
d σ =
cos
(8.4)
dQ2 M ott
Q4 E
2
Der erste Faktor im Mott-Querschnitt ist der wohlbekannte Rutherfordquerschnitt Gl. (8.2),
der für strukturlose, spinlose Teilchen abgeleitet wird und bei dem die Bewegung des Protons
nach dem Stoß vernachlässigt wird (ortsfestes Potential). Den Rückstoß kann man leicht durch
den Rückstoßfaktor E 0 /E berücksichtigen.
Der zweite Term in Gleichung (8.1) wird bei hohen Q2 wichtig. Er berücksichtigt den Spin
des Protons, der ein magnetisches Moment verursacht. Dieses tritt in Wechselwirkung mit dem
magnetischen Moment des Elektrons.
Prozeß
Elastische Streuung
e+p → e+p
4 − V ektoren k + P → k 0 + P 0
~ k 0 = (E 0 , E
~ 0 ), P 2 = P 0 2 = M 2
k = (E, E),
q = k − k0
Q2 = −q 2 = 4E E 0 sin2
θ
2
θ=Streuwinkel des Elektrons, M =Masse des Protons, Elektronmasse vernachlässigt.
8.2.2
Elastische Streuung an einer Ladungsverteilung
Bis hierher hatten wir es nur mit strukturlosen, punktförmigen Teilchen zu tun. Man kann
sich nun auch überlegen, wie man eine “Verschmierung” der Ladung und des magnetischen
Momentes über ein endliches Volumen berücksichtigt. Das wird hier nicht abgeleitet, sondern
nur skizziert. Man ersetzt zunächst das ortsfeste Coulombpotential durch das Potential einer
Ladungsverteilung mit einer Ladungsdichte ρ(~r):
164
Tiefunelastische Streuung: Struktur des Nukleons
e2
α
VP unkt (r) = −
=−
4π0 r
r
→
V (r) = −α
Z
d3 r 0 ρ(r~0 )
|~r − r~0 |
R
mit d3 r 0 ρ(r 0 ) = 1.
Man definiert einen Formfaktor als Fouriertransformierte der Ladungsverteilung:
Z
~0
2
F (~q ) = d3 r 0 ρ(r~0 ) ei~q r
Man bekommt einen modifizierten Wirkungsquerschnitt:
dσ dσ =
|F (~q 2 )|2 .
dΩ ρ
dΩ P unkt
Der Dreierimpulsübertrag zwischen Elektron im Anfangs und Endzustand ist: q~ = ~k − k~0 .
Durch Vergleich von gemessenem und Punktwirkungsquerschnitt kann man auf die Form der
Ladungsverteilung schliessen und z.B. ihren mittleren Radius bestimmen.
Messungen an Kernen sind in Abbildungen 8.2 zu sehen. Die Korrelation zwischen räumlicher
Ladungsverteilung und Formfaktor als Funktion von |~q| ist in Abb. 8.3 links illustriert. Radiale
Ladungsverteilungen einiger Kerne sind in Abb. 8.3 rechts zu sehen.
8.2.3
Elastische Elektron Proton Streuung
Man muß berücksichtigen, daß Elektron und Proton nicht nur über ihre Ladung, sondern, da sie
beide Spin 12 haben, auch über die magnetischen Momente wechselwirken. Daher bekommt man
zwei Formfaktoren, einen elektrischen GE und einen magnetischen GM . Bei der Streuung am
Nukleon muß man berücksichtigen, daß es Energie aufnimmt. Daher hängen die Formfaktoren
vom Viererimpulsübertrag Q2 ab. Der Wirkungsquerschnitt ist:
2
dσ GE + τ G2M
dσ
2
2
2 θ
=
+ 2 τ GM (Q ) tan
(8.5)
dΩ
dΩ M ott
1+τ
2
Q2
τ =
(8.6)
4M 2
Dieser Ausdruck wird Rosenbluthformel genannt. Folgende Normierungen sind üblich:
GpE (0) = 1
GnE (0) = 0
GpM (0) = µp GnM (0) = µn
wo µp = 2.79 und µn = −1.91 die anomalen magnetischen Momente des Protons und Neutrons
sind.
Man sieht in Gl. 8.5, daß die Formfaktoren sich bestimmen lassen aus Messungen des Wirkungsquerschnitt als Funktion des Streuwinkels θ. Man findet, daß die Formfaktoren im Bereich
mittlerer Q2 recht genau der sogenannten Dipolform folgen:
GM (Q2 )
=
GE (Q2 ) =
µp
1
1+
Q2
0.712
!2
,
wobei Q2 in GeV2 einzusetzen ist und µp das anomale magnetische Moment des Protons ist.
8.2 Elastische Streuung
Abbildung 8.2: Links: Messung des Formfaktors von 12 C durch Elektronenstreuung. Gezeigt ist
der differentielle Wirkungsquerschnitt, der bei einer festen Strahlenenergie von 420 MeV gemessen wurde. Rechts: Differentielle Wirkungsquerschnitte für die Streuung von Elektronen an
den Kalziumisotopen 40 Ca und 48 Ca. Zur besseren Darstellung wurde der Wirkungsquerschnitt
für 40 Ca mit 10−1 multipliziert.
Abbildung 8.3: Links: Zusammenhang zwischen radialer Ladungsverteilung und Formfaktor in
Bornscher Näherung. Einem konstanten Formfaktor entspricht eine punktförmige Ladung (z.B.
Elektron), einem sogenannten Dipol-Formfaktor eine exponentiell abfallende Ladungsverteilung (z.B. 6 Li-Kern) und einem oszillierenden Formfaktor eine homogene Kugel mit mehr oder
minder scharfem Rand. Alle Kerne, mit Ausnahme der ganz leichten, haben einen oszillierenden Formfaktor. Rechts: Radiale Ladungsverteilung einiger Kerne. Diese Ladungsverteilungen
können näherungsweise als Kugeln mit diffusem Rand durch die Fermi-Verteilung beschrieben
werden.
165
166
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.4: Die Protonformfaktoren als Funktion von Q2 .
Der differentielle Wirkungsquerschnitt für elastische Streuung nimmt also sehr rasch ab mit
wachsendem Q2 . Der Mott-Querschnitt alleine nimmt schon mit 1/Q4 ab. Hat man eine ausgedehnte Ladungsverteilung, so nimmt der Wirkungsquerschnitt relativ dazu etwa mit 1/Q4 ab,
insgesamt also mit ∼ 1/Q8 ! Bei hohen Q2 ist elastische Streuung also beliebig unwahrscheinlich.
Was passiert dort? Das Proton wird zerstört, man hat unelastische Streuung.
8.3
Unelastische Streuung
Das Diagramm für den unelastischen Prozeß e + p → e + X kann man wie folgt andeuten
(in Klammern sind die Vierervektoren, der schwarze Kreis am unteren Vertex deutet an “hier
passiert etwas Unbekanntes”, d.h. etwas, was im ursprünglichen Formalismus nicht enthalten
ist):
e− (k 0 )
e− (k)
γ(q)
p(P )
X(P 0 )
Trägt man den Wirkungsquerschnitt für diesen Prozeß wieder im Verhältnis zum Mott-Querschnitt
auf, so sieht man etwas ganz Erstaunliches (Abb. 8.5): Das Verhältnis ist praktisch unabhängig
von Q2 . Erinnern wir uns, daß der Mott-Querschnitt für die Streuung an strukturlosen Objekten gilt, so vermuten wir, daß wir jetzt offenbar an strukturlosen Objekten elastisch streuen.
8.3 Unelastische Streuung
167
Diese Vermutung ist tatsächlich wahr, die Streuung findet an den Quarks statt.
8.3.1
Kinematik von unelastischer Streuung
Dadurch, daß jetzt ein hadronisches System X erzeugt wird, dessen Masse unbekannt und nicht
konstant ist, hat man zwei unabhängige Variable. Bei elastischer Streuung war nur eine Variable
unabhängig, man wählte z.B. θ oder Q2 . Die Energie des gestreuten Elektrons ist bei elastischer
Streuung festgelegt, wenn man den Streuwinkel vorgibt. Bei unelastischer Streuung kann man
als zweite unabhängige Variable die Energie des gestreuten Elektrons E 0 wählen. Üblicherweise
drückt man die Wirkungsquerschnitte aber in invarianten Größen aus. Dann kann man Q2 und
beispielsweise die dimensionslose Variable x wählen. Die Definition der kinematischen Variablen
ist in Tabelle 8.1 zusammengefaßt.
Die Masse des Systems X in der unelastischen Reaktion e + p → e + X sei W , W 2 = P 02 .
W 2 = P 02 = (q + P )2
= q 2 + M 2 + 2q · P
= −Q2 + M 2 + 2(E − E 0 )Ep − 2(~k − k~0 ) p~p
= −Q2 + M 2 + 2(E − E 0 )M
im Proton-Ruhesystem
(8.7)
(8.8)
(8.9)
(8.10)
Der letzte Schritt ist gültig im Ruhesystem des Protons, dort gilt P = (M, 0), wobei M die
Ruhemasse des Protons ist.
Abbildung 8.5: Elektron-Proton-Streuung: gemessener Wirkungsquerschnitt normiert auf den
Mott-Wirkungsquerschnitt als Funktion von Q2 für verschiedene Werte der invarianten Masse
W.
168
Tiefunelastische Streuung: Struktur des Nukleons
Kinematik Tiefunelastische Streuung
Prozeß
e+p → e+X
4 − V ektoren k + P = k 0 + P 0
~ k 0 = (E 0 , E
~ 0 ), P 2 = M 2 , P 0 2 = W 2
k = (E, E),
q = k − k0 = P 0 − P
Invarianten
Proton Ruhesystem
Q2 ≈ 4 E E 0 sin2
s ≈ 2M E
Q2 = −q 2
s = (k + P )2
P ·q
ν=
M
Q2
Q2
=
x =
2P ·q
2M ν
P ·q
y =
P ·k
θ
2
ν = E − E0
Q2
x =
2 M (E − E 0 )
ν
E − E0
=
y=
E
E
Q2 = x y s
Tabelle 8.1: Definition der kinematischen Größen für unelastische Lepton Nukleonstreuung
Man definiert die lorentzinvarianten Größen:
P ·q
M
Q2
x =
2P ·q
(8.11)
ν =
(8.12)
Letztere Größe x ist eine der beiden “Bjorken Skalenvariablen”, die man oft zusätzlich zu Q2
(oder auch zu y) alszweite Variable benutzt. Aus Gl. (8.11) und (8.12) folgt:
Q2
x=
2M ν
Anschauliche Bedeutung gewinnen diese Variablen im Ruhesystem des Protons. Aus Gl. (8.11)
folgt dort:
ν = E − E0
im p-Ruhesystem
Aus den letzten beiden:
x=
Q2
2 M (E − E 0 )
im p-Ruhesystem
D.h. man kann x aus Größen bestimmen, die nur vom gestreuten Elektron abhängen, E 0 und
Q2 . Man braucht nichts über das System X zu wissen.
Aus Gl. (8.8) mit (8.12) folgt:
W 2 = −Q2 + M 2 +
Q2
x
8.3 Unelastische Streuung
Abbildung 8.6: Spektrum der gestreuten Elektronen bei Elektron-Positron-Streuung, aufgenommen bei einer Elektronenenergie E = 4.9 GeV unter einem Streuwinkel θ = 10◦ (DESY
Daten).
Die elastische Streuung ist der Grenzfall: W 2 = M 2 , dann ist x = 1 wie man an letzter Beziehung
sieht. Bei unelastischer Streuung dagegen hat man W 2 > M 2 und x < 1. Bei elastischer
Streuung ist x also fest, während es bei unelastischer Streuung als eine zweite Variable zusätzlich
zu Q2 gewählt werden kann. In Abb. 8.6 ist der doppelt differentielle Streuquerschnitt als
Funktion von E 0 und in einer zweiten Skala als Funktion von W zu sehen, W ≥ M . Man
sieht bei W = M einen riesigen Wert (elastische Streuung), dann weitere Maxima bei größeren
Werten von W , die angeregten Zuständen des Nukleons entsprechen. Das wichtigste ist aber,
daß der Querschnitt auch bei den größten Werten von W recht groß bleibt.
Diese Tatsache wird in Abb. 8.5 noch einmal etwas anders dargestellt. Hier ist das Verhältnis
des gemessenen Wirkungsquerschnitts zum Mottquerschnitt bei festem W als Funktion von Q2
aufgetragen. In logarithmischer Skala sieht man sehr schön, dass dieses Verhältnis praktisch
unabhängig von Q2 ist, während der elastische Wirkungsquerschnitt im selben Bereich um
mehrere Zehnerpotenzen fallen würde.
8.3.2
Quark Parton Modell
Wir nehmen jetzt an, daß die anfangs ausgesprochene Vermutung wahr ist, daß also das Nukleon
aus Quarks qi besteht2 . Wir gehen in ein System, in dem das Proton so schnell ist, daß wir alle
Transversalimpulse vernachlässigen können. Man nennt dieses System das “Infinite Momentum
Frame”, bei HERA ist es praktisch durch das Laborsystem realisiert. Das Nukleon kann als ein
Strom von Quarks betrachtet werden, von denen eins mit dem virtuellen Photon kollidiert, das
zwischen Elektron und Quark ausgetauscht wird. Die Impulse seien groß genug, so daß auch
Massen vernachlässigt werden können. Man kann den Viererimpuls p des Quarks, welches mit
dem Photon kollidiert, im Infinite Momentum Frame als Bruchteil z des Viererimpulses des
Protons, p = z · P ansetzen, wobei 0 ≤ z ≤ 1.
2
Als die Messungen gemacht wurden und man versuchte, sie zu verstehen, war es noch nicht klar, ob Quarks
existieren. Deshalb hat man die Konstituenten zunächst vorsichtig ‘Partonen’ genannt.
169
170
Tiefunelastische Streuung: Struktur des Nukleons
e± (k 0 )
±
e (k)
γ(q)
Quark(p)
Proton Rest
Gestreutes Quark: p0
Berechnung von z:
Sei P der Protonviererimpuls, p = zP der des Quarks, welches mit dem ausgetauschten Photon
~ −E
~ 0 ) der Photonvierimpuls.
kollidiert, und q = (E − E 0 , E
0
(q + zP )2 = p 2 = m2q ≈ 0
q 2 + (z P )2 + 2 q z P ≈ 0.
Es ist (z P )2 = p2 = m2q Q2 , wobei Q2 = −q 2 ist. Damit folgt:
z=−
Q2
q2
=
=x
2q · P
2q · P
(8.13)
nach Definition von x. Wir bekommen also das wichtige Ergebnis:
z = x.
In diesem System (Infinite Momentum Frame) gibt x also den Impulsbruchteil des Protons an,
den das Quark trägt, an dem die elastische Streuung passiert. Da man x messen kann, kann
man den Relativimpuls des Quarks bestimmen, an dem die Streuung stattfindet. Dabei genügen
Meßgrößen des gestreuten Elektrons.
Der Wirkungsquerschnitt für die elastische Streuung eqi → eqi (qi = Quark der Ladung ei e)
ist gegeben durch den Querschnitt (Gleichung (8.3)):
dσ dσ Q2
2 θ
tan
· e2i
=
1+
2
2
2
dQ eqi
dQ M ott
2mq
2
(8.14)
mq ist die Quarkmasse und ei e die Quarkladung.
Den Wirkungsquerschnitt am Proton schreiben wir versuchsweise als inkohärente Summe über
diesen Wirkungsquerschnitt:
X dσ dσ · fi (x) dx
=
(8.15)
2
dQ2 ep
dQ
eq
i
i
fi (x) dx bezeichnet die Wahrscheinlichkeit, das Quark qi im Impulsintervall (x, x + dx) anzutreffen. Wenn dieses Bild richtig ist, so versteht man, warum das Verhältnis des gemessenen
Wirkungsquerschnitts zum Mott-Querschnitt (fast) unabhängig von Q2 ist.
8.3 Unelastische Streuung
171
Diese Unabhängigkeit von Q2 wurde experimentell gefunden vor der Etablierung des Quarkmodells. Man nannte das Verhalten: “SKALENVERHALTEN”. Es war theoretisch vorausgesagt
durch Bjorken auf Grund ganz anderer Überlegungen3 .
Historisch wurde der Wirkungsquerschnitt in Gl. (8.15) folgendermaßen geschrieben:
X
dσ d2 σ (8.16)
=
·
e2i fi (x)
dQ2 dx ep
dQ2 P unkt i
{z
}
|
F2 /x
F2 wird als Strukturfunktion bezeichnet im Gegensatz zu den bei elastischer Streuung definierten Formfaktoren. Aus den gemessenen doppelt differentiellen Wirkungsquerschnitten bestimmt man F2 (x, Q2 ) und trägt es gegen Q2 auf, Abb. 8.11. Man sieht, daß F2 in der Tat (fast)
unabhängig ist von Q2 , insbesondere im Bereich nicht zu kleiner Werte von x. Die leichte beobachtete Abhängigkeit ist wesentlich weniger stark als die des elastischen Wirkungsquerschnitts
(z.B. Abb. 8.5).
Im allgemeinen gibt es zwei Strukturfunktionen entsprechend den beiden Termen im Wirkungsquerschnitt (8.3) und den beiden Formfaktoren bei der elastischen Streuung am Proton.
4πα2 2
d2 σ
=
y xF1 (x, Q2 ) + (1 − y) F2 (x, Q2 )
2
4
dQ dx
xQ
(8.17)
hierbei ist y die zweite Bjorkenvariable. Sie ist leicht zu bestimmen aus:
y=
(s. Tabelle 8.1). Falls die Streuung an Spin
den beiden Strukturfunktionen:
1
2
Q2
xs
Teilchen erfolgt, so gibt es eine Beziehung zwischen
F2 (x, Q2 ) = 2 x F1 (x, Q2 ).
Diese Beziehung heißt Callan-Gross Beziehung. Für Spin 0 Teilchen würde gelten: F1 (x, Q2 ) = 0.
In Abb. 8.8 sieht man, daß die Daten den Spin 12 der Targetteilchen bestätigen.
8.3.3
Quarkverteilungen im Nukleon
Die Messung des doppelt differentiellen Wirkungsquerschnitts nach Gl. (8.16) oder (8.17) liefert
einem F2 (x, Q2 ). Die geringfügige Abhängigkeit von Q2 vernachlässigen wir zunächst. Nach Gl.
(8.15) liefert einem F2 (x) direkten Zugang zu den Relativimpulsverteilungen der Quarks im
Proton:
F2 (x) X 2
=
ei (qi (x) + q i (x))
x
i
Wir haben hier gleich angenommen, daß es außer Quarks mit der Verteilung qi (x) auch Antiquarks mit q i (x) gibt4 . Quelle für Antiquarks sind Abstrahlungen von Gluonen, die dann
wieder in Quark-Antiquark Paare fluktuieren. Diese zusätzlich zu den Valenzquarks existierenden Quarks und Antiquarks nennt man auch Seequarks. Für das Proton kann man dann
3
4
Ihm zu Ehren nennt man die sogenannten Skalenvariablen x und y auch die “Bjorkenvariablen”.
Der Einfacheit halber verwenden wir jetzt die Notation qi (x) anstelle von fqi (x) im vorigen Abschnitt
172
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.7: Die Strukturfunktion F2 (historisch wurde sie ν W2 genannt), die in Elektron
Proton Streuung bei x = 0.25 als Funktion von Q2 gemessen wurde (ω = 1/x).
Abbildung 8.8: Das Verhältnis 2xF1 /F2 , gemessen in Elektron-Nukleon-Streuexperimenten am
SLAC. Für Spin- 1/2 Partonen erwartet man, daß dieses Verhältnis im Grenzfall großer q 2
gegen Eins geht – die Callan-Gross-Relation. (Die Datenpunkte stammen aus verschiedenen
publizierten SLAC-Resultaten.)
8.3 Unelastische Streuung
173
schreiben:
F2ep = x
X
e2i (qi (x) + q̄i (x))
(8.18)
i
F2ep
#
" 2
2
2
1
= x
dp (x) + d¯p (x) ,
(up (x) + ūp (x)) +
3
3
(8.19)
Es wurden nur u und d Quarks berücksichtigt. Analog gilt für das Neutron (die Strukturfunktionen des Neutrons bekommt man indirekt über Messungen am Deuterium):
" #
2
2
2
1
dn (x) + d¯n (x) ,
F2en = x
(8.20)
(un (x) + ūn (x)) +
3
3
Nun hat man viel zu viele unbekannte Funktionen. Indem man Isospininvarianz benutzt, d.h.
man nimmt an, daß die u Verteilungen im Proton gleich den d Verteilungen im Neutron sind,
bekommt man Beziehungen zwischen den Verteilungen:
u(x) ≡ up (x) = dn (x)
d(x) ≡ dp (x) = un (x)
und
(8.21)
(8.22)
Außerdem separieren wir Valenzquarks und der Seequarks:
u(x) ≡ uV (x) + uSee (x),
d(x) ≡ dV (x) + dSee (x).
(8.23)
(8.24)
Zusätzlich nimmt man an, daß alle Seequarkverteilungen gleich sind.
¯ ≡ S(x)
uSee (x) = dSee (x) = ū(x) = d(x)
Für das Proton, welches danach aus |uud + Seei besteht, bekommt man dann:
" #
2
2
2
1
F2ep (x) = x
upV (x) +
dpV (x) + e2See S(x)
3
3
(8.25)
Analog für das Neutron:
F2en
#
" 2
2
1
2
unV (x) +
dnV (x) + e2See S(x)
=x
3
3
(8.26)
Der See ist dann mit diesen Annahmen in beiden Fällen:
e2See S(x) =
4
1
10
¯
(uSee (x) + ū(x)) + (dSee (x) + d(x))
=
S(x)
9
9
9
Benutzt man auch Isospininvarianz, so gilt:
F2ep (x)
1
= [4 uV (x) + dV (x)] +
x
9
F2en (x)
1
= [uV (x) + 4 dV (x)] +
x
9
10
S(x)
9
10
S(x)
9
(8.27)
(8.28)
174
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.9: Die Differenz von F2 aus Elektronenstreuung an Protonen und Neutronen als
Funktion von x.
Man kann z.B. die Differenz der Messungen von F2 bilden:
F2ep (x) − F2en (x) =
1
x [uV (x) − dV (x)]
3
Man bekommt also eine Verteilung der Valenzquarks. Diese Differenz ist in Abb. 8.9 gezeigt.
Man sieht ein (breites) Maximum bei 1/3, wie man es bei 3 Quarks auch erwarten würde.
Eine weitere Folgerung über die Verteilung der Valenz- und Seequarks in x mit diesen Annahmen
werden in einer Übungsaufgabe behandelt.
8.3.4
Quarkladungen
Einen der schlagendsten Beweise dafür, daß es sich bei den Streuzentren tatsächlich um Quarks
handelt, liefert der Vergleich mit Strukturfunktionen von Messungen mit Neutrinos. Die untersuchte Reaktion ist:
νµ + N → µ − X
und
ν µ + N → µ+ X.
Es gibt einen wesentlichen Unterschied zur Streuung an Elektronen: für die elektromagnetische
Wechselwirkung ist die elektrische Ladung wichtig, das bei Neutrinowechselwirkungen ausgetauschte W Boson koppelt gleich stark an alle Quarks. Wir haben also in Analogie zu Gl. (8.19)
und (8.20):
¯
F2νN = x u(x) + ū(x) + d(x) + d(x)
N bedeutet hierbei “Nukleon” und F2νN = 0.5 (F2νp + F2νn ). Analog bildet man für die Streuung
von Elektronen:
F2eN = 0.5 (F2ep + F2en ) =
4 p
1 p
4 n
1 n
1
p
p
n
n
¯
¯
x
(u (x) + ū (x)) + (d (x) + d (x)) + (u (x) + ū (x)) + (d (x) + d (x))
2
9
9
9
9
8.4 Gluonen
175
und mit Isospininvarianz:
F2eN =
Also
5 1
¯
·x·
u(x) + ū(x) + d(x) + d(x)
2
9
5 νN
F (x).
18 2
Diese Beziehung wird sehr schön durch die Daten bestätigt (Abb. 8.10).
F2eN (x) =
8.3.5
Quarkimpulssummen
Eines der überraschenden Ergebnisse der ersten Messungen von Strukturfunktionen hängt mit
der Erwartung für die Summe über alle Relativimpulse zusammen. Hat man nur Quarks und
Antiquarks im Nukleon, so würde man bekommen:
Z 1
Z 1
?
ep
dx x F2 (x) =
dx x (u + u + d + d + s + s + . . . ) = 1
0
0
Wobei die Punkte . . . andeuten, daß es eventuell noch weitere kleine Anteile von schweren
Quarks geben könnte. In Wahrheit fand man aber einen Wert von ungefähr 0.5 und zwar
sowohl in Messungen mit Elektronen als auch mit Neutrinos. D.h. ein erheblicher Bruchteil des
Nukleonenimpulses wird nicht von Quarks/Antiquarks getragen sondern von einer Komponente,
die weder mit Elektronen noch mit Neutrinos wechselwirkt. Eine naheliegende Vermutung ist,
daß die Gluonen den Rest des Impulses tragen. Wir setzen an, daß das obige Integral ergibt:
1 − g , wobei g den Bruchteil des Relativimpulses bezeichnet, den die Gluonen tragen.
Z 1
dx x F2ep(x) = 1 − g
0
Man kann dann (wieder mit Vernachlässigung der s Quarks) schreiben:
Z 1
4
1
dx x F2ep (x) = pu + pd = 0.18
9
9
Z 01
4
1
dx x F2en (x) = nu + nd = 0.12
9
9
0
R
1
Dabei ist pu = 0 dxx (up (x) + up (x)). Die Zahlen kommen aus Messungen. Mit der Annahme
von Isospininvarianz berechnet man daraus:
pu = 0.36
und damit hat man:
pd = 0.18
g = 1 − pu − pd = 0.46.
Der Protonimpuls wird zum großen Teil von Gluonen getragen!
8.4
Gluonen
Durch Messung der Strukturfunktion F2 in tiefunelastischer Streuung bekommt man also Information über die Objekte, an denen die Streuung stattfindet. Wir haben gesehen, daß es sich
dabei um Quarks und Antiquarks handelt. Es ist aber auch ein beträchtlicher Anteil von Gluonen vorhanden, auf die man nur indirekt schließen kann, da weder Elektronen noch Neutrinos
mit ihnen in Wechselwirkung treten. Information über Gluonen im Nukleon haben insbesondere
auch die Untersuchungen am Elektron Proton Speicherring HERA gebracht.
176
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.10: Daten von tief unelastischer Neutrino- und Myon-Streuung für F2 . Man sieht,
daß die Daten übereinstimmen, wenn man die von den geladenen Leptonen mit 18/5 multipliziert. Die Faktoren nahe 1, die zusätzlich berücksichtigt sind, gleichen nur die Normierung
der verschiedenen Experimente an. (xF3 und die Seeverteilung q kann aus Neutrinostreuung ist
zusätzlich gezeigt.)
8.4 Gluonen
Strukturfunktion F2 (x, Q2 ) bei HERA
log Q
2
8.4.1
177
5
H1 + ZEUS
HERMES
4
E665
y
=
1
BCDMS
3
CCFR
SLAC
2
NMC
1
0
y
=
0.
00
5
-1
-6
-5
-4
-3
-2
-1
log x
Abbildung 8.10: Die ’kinematische Ebene’. Als Funktion von x und Q2 sind die von bisherigen
Experimenten vermessenen Bereiche gezeigt. Alle Experimente, bis auf H1 und ZEUS, sind
Fest-Target Experimente.
In Abb. 8.10 ist gezeigt, in welchen Bereichen von x und Q2 bisher Messungen der Protonstruktur durchgeführt wurden. Die früheren Fest-Target Experimente, bei denen das Proton im
Laborsystem ruht, haben eine niedrigere Schwerpunktsenergie. Dort können für heutige Verhältnisse nur kleine Werte von Q2 , Q2 ≤ 100 GeV2 , erreicht werden. Der in x zugängliche Bereich
ist beschränkt auf größere Werte von x ≥ 10−3 . Die am ep Speicherring HERA (Experimente
H1 und ZEUS) erreichbaren Werte von Q2 sind etwa zwei Größenordnungen größer, die x-Werte
zwei Größenordnungen kleiner, als bei den Fest-Target Experimenten.
Bereits im ersten Jahr der Datennahme wurde bei HERA beobachtet, daß die Protonstrukturfunktion F2 (x, Q2 ) als Funktion von x, bei festem Q2 , im Bereich x ≤ 10−2 zu kleinen x stark
ansteigt. Figur 8.11 zeigt Daten von H1 und ZEUS aus den Jahren 96-97 im Vergleich mit
Daten von Fest-Target Experimenten bei größeren Werten von x. Die Fest-Target Daten allein
zeigen keinen deutlichen Anstieg von F2 zu kleinen x.
Der Anstieg von F2 (x) zu kleinen x zeigt, daß die Anzahl der Quarks im Proton zu kleinen x
zunimmt. Dabei handelt es sich offenbar um Seequarks, die durch Paarerzeugung aus Gluonen,
produziert werden können. Anschaulich gesprochen, steigt F2 (x) zu kleinen x hin an, weil die
Seequarks nur einen geringen Bruchteil des Gesamtprotonimpulses übernehmen. Die Gluonen,
aus denen Seequark und -antiquark paarweise gebildet werden können, entstehen durch den
Prozess der Gluonbremsstrahlung und haben selbst nur kleine Impulsanteile, denn das Bremsstrahlungsspektrum fällt mit 1/k ab.
In Figur 8.12 sind die F2 -Daten aufgetragen als Funktion von Q2 für verschiedene feste Werte
von x. Um die verschiedenen Werte von x in derselben Abbildung zeigen zu können und dabei
178
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.11: Die Strukturfunktion F2 (x, Q2 ) als Funktion von x bei einem festen Wert von
Q2 = 15 GeV2 . Vor HERA erreichten die Fest-Target Experimente Werte von x ≥ 0.01.
Überschneidungen zu vermeiden, sind die Daten für jeden Wert von x um einen von x abhängigen Wert versetzt. Bei kleinen Werten von Q2 (Q2 < 200 GeV2 ) und größeren Werten von x
(x ≥ 0.005) sind wieder Fest-Targetdaten gezeigt. Wie im vorherigen Abschnitt diskutiert zeigen diese Daten näherungsweise ein ’Skalenverhalten’, d.h. F2 (x, Q2 ) ist unabhängig von Q2 für
feste Werte von x. Im Gegensatz zum Skalenverhalten von F2 bei größeren x zeigen die HERA
Daten, daß F2 (x, Q2 ) zu kleinen x hin abhängig wird von Q2 . Dieser Effekt, der in geringerem
Maße auch schon von den Experimenten vor HERA beobachtet wurde, wird ’Skalenverletzung’
genannt und ist auf die Existenz von Gluonen zurückzuführen.
Um den Effekt der Skalenverletzung anschaulich zu verstehen, muß berücksichtigt werden, daß
die Größe Q2 mit der Compton-Wellenlänge zusammenhängt (siehe auch Abschnit 8.1), die
die Auflösung bestimmt. Mit zunehmendem Q2 wird die Compton-Wellenlänge kleiner und es
werden kleinere und kleinere Strukturen im Proton aufgelöst. Skalenverletzung bedeutet also,
daß zu größeren Werten von Q2 mehr und mehr aus Gluonen produzierte Seequarks ’gesehen’
werden, so daß der ep-Wirkungsquerschnitt, und damit F2 (x, Q2 ) zu größeren Werten von Q2
ansteigt.
8.4.2
QCD-Dynamik
Im Rahmen der QCD (Quanten Chromodynamik) werden die Wechselwirkungen zwischen
Quarks und Gluonen quantitativ beschrieben. Auf der Grundlage von QCD Rechnungen kann
ein genauer Zusammenhang zwischen dem Verhalten der Strukturfunktion F2 (x, Q2 ) und den
Valenzquark-, Seequark- und Gluonverteilungen im Proton berechnet werden (mit Gleichungen von Dokshitzer, Gribov, Lipatov, Altarelli, Parisi, abgekürzt “DGLAP”). Mit Hilfe der
DGLAP-Gleichungen und einigen Impulssummenregeln (siehe voriger Abschnitt und Aufgaben
36, 37, 38) können die Partonverteilungen einschließlich der Gluonverteilungen aus den experimentell bestimmten Werten von F2 (x, Q2 ) durch Anpassungen an die Daten (’Fits’) ermittelt
F2+ci(x)
8.4 Gluonen
179
SLAC
NMC
BCDMS
x=0.000032
x=0.00005
H1 96-97 preliminary
x=0.00008
x=0.00013
(i=20)
+
H1 94-97 e p
x=0.0002
x=0.00032
NLO QCD Fit
x=0.0005
x=0.0008
x=0.0013
ci(x)= 0.6 • (i(x)-0.4)
x=0.002
x=0.0032
x=0.005
x=0.008
x=0.013
(i=10)
x=0.02
x=0.032
x=0.05
x=0.08
x=0.13
x=0.18
x=0.25
x=0.40
x=0.65
1
10
10
2
10
3
10
4
2
10
(i=1)
5
Q /GeV
2
Abbildung 8.12: Die Strukturfunktion F2 (x, Q2 ) als Funktion von Q2 für feste Werte von x.
F2 (x, Q2 ) ist für die verschiedenen x-Werte um jeweils einen Wert ci (x) = 0.6(i(x) − 0.4)
verschoben.
180
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.13: Links: Die Absorption von Photonen durch das Nukleon. Ist die Wellenlänge
groß, so kann man nur die Größe des Nukleons messen. Bei genügend kleiner Wellenlänge sind
auch Strukturen zu ‘sehen’. Rechts: das Bild des Nukleons in QCD mit Valenzquarks, Gluonen
und Seequarks.
Abbildung 8.14:
8.4 Gluonen
181
werden.
In erster Näherung (niedrigste Ordnung Störungsrechnung) gilt bei kleinen x:
dF2 (x, Q2 )
∼ αs (Q2 ) · x · g(x)
2
d ln Q
(8.29)
H1 Collaboration
Man erkennt aus Gleichung (8.29), daß die Änderung von F2 mit Q2 direkt von der Gluonverteilung abhängt. Bei kleinen x bestimmt also die Anzahl der Gluonen im Proton das Verhalten
von F2 (x, Q2 ). Aus der Beobachtung der Skalenverletzung und dem Anstieg von F2 zu kleinen
x bei festem Q2 kann man darauf schließen, daß die Anzahl der Gluonen im Proton zu kleinen
x hin ansteigt.
Abbildung 8.15: Die mit Hilfe der DGLAP-Gleichungen durch Anpassung an die F2 -Daten
ermittelte Verteilung der Gluonen im Proton (multipliziert mit x) als Funktion von x bei einem
festen Wert von Q2 = 5GeV2 .
In Abb. 8.15 ist die aus Anpassungen an die Daten ermittelte Verteilung der Gluonen im Proton
gezeigt. Man erkennt einen steilen Anstieg zu kleinen x.
Die verschiedenen Partonverteilungen von u-Valenzquarks, d-Valenzquarks, Seequarks und Gluonen im Proton sind in Abb. 8.16 gezeigt. Die Valenzquarkverteilungen ähneln den im vorigen
Abschnitt aus dem Vergleich von Proton und Neutrondaten ermittelten Verteilungen. Sie zeigen ein Maximum bei Werten von x ∼ 0.2, etwas kleiner als das naive 0.3. Die Seequarks und
Gluonen sind in der Abbildung um einen Faktor 0.05 skaliert. Sie steigen zu kleinen Werten
von x steil an. Dabei dominieren die Gluonen.
QCD–Bild des Protons
Zusammenfassend stellt sich das Bild des Protons anschaulich folgendermaßen dar (Abb. 8.14):
182
Tiefunelastische Streuung: Struktur des Nukleons
Abbildung 8.16: Übersicht über die aus F2 -Daten mit Hilfe der DGLAP-Gleichungen ermittelten
Relativimpulsverteilungen von Partonen im Proton als Funktion von x bei festem Q2 = 10
GeV2 . x uV und x dV bezeichnen die u und d-Valenzquarkverteilungen. Die Seequarkverteilung
ist xS und xg, die Gluonverteilung xg. Sie sind um einen Faktor 0.05 skaliert.
• Das Proton besteht aus Valenzquarks, Seequarks und Gluonen. Die Valenzquarks sind
entscheidend bei großen Werten von x. Sie tragen gemeinsam etwa die Hälfte des Protonenimpulses.
• Zu kleinen Werten von x steigt die Gluonverteilung stark an. Es gibt viele Gluonen im
Proton. Die einzelnen Gluonen tragen i.a. nur einen geringen Anteil des Protongesamtimpulses.
• Skalenverletzungen, d.h. eine Abhängigkeit von F2 von Q2 treten auf, weil die aus Gluonen
produzierten Seequarks bei höheren Q2 sichtbar werden.
Die HERA-Experimente haben einen großen kinematischen Bereich großer Q2 und kleiner x
ausgemessen. Die hier dargestellten Befunde werfen drei wesentliche Fragen auf:
• Wie präzise ist unser Verständnis der QCD? Sind die Rechnungen und die zur Lösung
der Gleichungen notwendigen Näherungen (z.B. die DGLAP-Gleichungen) korrekt? In
welchen Bereichen verlieren die Näherungen ihre Gültigkeit?
8.5 Die Suche nach Quarksubstruktur
• Was passiert bei kleinsten Werten von x, jenseits des gegenwärtig zugänglichen Bereichs?
Steigt die Verteilung der Gluonen und Seequarks weiter an? Theoretiker erwarten Sättigung, also ein Abflachen der Steigung, wenn die Zahl der Gluonen und Seequarks so groß
wird, daß sich ihre Wellenfunktionen signifikant überlappen.
• Sind Quarks wirklich punktförmig, oder haben sie eine Ausdehnung? Messungen bei den
höchsten Werten von Q2 geben eine maximale Auflösung. Dort könnten Hinweise auf einen
endlichen Quarkradius oder eine Quarksubstruktur gefunden werden.
Diese und andere Fragen sind Gegenstand der heutigen Forschung. In dieser Vorlesung beleuchten wir kurz Untersuchungen zu zwei der drei obigen Fragestellungen.
8.4.3
QCD-Konsistenztests
Die Ergebnisse aus den Messungen der Protonstrukturfunktion F2 können verifiziert werden,
indem andere Prozesse als Elektron-Proton Streuung untersucht werden. Partonverteilungen
sind universell, d.h. sie beschreiben die Struktur des Protons unabhängig vom Streuprozeß. Für
den Fall, daß die QCD Rechnungen korrekt sind, sollten also die gleichen Partonverteilungen
herauskommen.
Zum Beispiel kann die Messung von Charm-Quarks ausgenutzt werden, um Aufschluß über
die Verteilung der Gluonen zu erhalten. Charmseequarks können paarweise aus Gluonen entstehen. Das ausgetauschte virtuelle Photon kann an einem Charm-Seequark streuen. In der
Hadronisierung, die mit dem Aufbrechen des Protons in der unelastischen Streuung einhergeht,
bilden die Charm-Quarks Hadronen mit Charminhalt, z.B. D ∗+ -Mesonen. Die D ∗+ Mesonen
können experimentell durch ihren Zerfall D ∗+ → D 0 π + und nachfolgend D 0 → K − π + anhand
der Zerfallsteilchen π + π + K − nachgewiesen werden. Aus der Messung der Impulsverteilung der
D ∗+ Mesonen kann dann die Verteilung der an der Charmquarkproduktion beteiligten Gluonen
ermittelt werden. Ein Ergebnis ist in Fig. 8.16 gezeigt. Man erkennt gute Übereinstimmung
zwischen der aus F2 ermittelten Verteilung der Gluonen (Band) und den Punkten, die aus D ∗+
Messungen stammen. Die Genauigkeit der Messung ist noch beschränkt durch die geringe Anzahl der meßbaren Ereignisse (statistischer Fehler), die experimentellen Unsicherheiten in der
Rekonstruktion der D ∗+ Mesonen sowie theoretische Unsicherheiten. Theoretische Unsicherheiten entstehen in erster Linie durch die ungenaue Kenntnis der Masse des Charmquarks, mc ,
sowie die Annahmen über den Übergang c → D ∗+ in der Hadronisierung.
8.5
Die Suche nach Quarksubstruktur
Die bisherigen Messungen der Protonstruktur sind in Übereinstimmung mit der Annahme, daß
Quarks keine Ausdehnung haben, d.h. ihre elektrische Ladung in einem Punkt konzentriert ist.
Dieser Befund soll nun quantitativer untersucht werden. Nimmt man an, die Quarks hätten
einen Radius, so könnte man den Wirkungsquerschnitt wieder über den in Abschnitt 8.2.2
verwendeten Formfaktoransatz beschreiben:
dσ dσ =
|F (Q2 )|2 .
dQ2 ep gemessen
dQ2 ep punktförmig
Wie oben gezeigt, besitzt der Wirkungsquerschnitt an ausgedehnten Ladungen eine steilere
Q2 -Abhängigkeit als der Wirkungsquerschnitt an einer Punktladung. Für den Fall, daß Quarks
einen endlichen Radius besitzen, erwartet man also eine steilere Q2 -Abhängigkeit als berechnet.
183
184
Tiefunelastische Streuung: Struktur des Nukleons
2
xg(x,Q )
H1 96-97
22.5
2
20
2
Q =20 GeV
2
2
µ =25 GeV
H1 prel.
exp ⊕ thy
D* (DIS)
D* (γp)
17.5
15
12.5
10
7.5
5
2.5
0 -4
10
10
-3
10
-2
10
-1
x1
Abbildung 8.16: Gluonverteilung xg(x, Q2 ) als Funktion von x bei festem Q2 . Das Band zeigt die
aus F2 -Daten ermittelte Gluonverteilung. Die Punkte stammen aus Messungen von Ereignissen
mit D ∗ -Mesonen.
Umgekehrt kann der Quarkradius aus Abweichungen von der Erwartung ermittelt werden (s.
Übungsaufgabe):
Rq2 2
2
F (Q ) ≈ 1 −
Q.
6
Abb. 8.17 zeigt die neuesten Ergebnisse der Untersuchungen. In Abb. 8.17a sind Daten des
H1 Experiments gezeigt. Der Wirkungsquerschnitt dσ/dQ2 ist aufgetragen als Funktion von
Q2 . Über etwa zwei Größenordnungen in Q2 variiert der Wirkungsquerschnitt um sieben Zehnerpotenzen. Um mögliche Abweichungen der Daten von der Erwartung besser erkennen zu
können, ist in Abb. 8.17b das Verhältnis zwischen der Messung und der Erwartung gezeigt. Die
Daten stimmen im Rahmen der Fehler bis zu den größten Werten von Q2 mit der Erwartung
überein. Das ZEUS Experiment ist einen Schritt weiter gegangen. Aus den Abweichungen im
Verhältnis zwischen Daten und Erwartung kann eine Obergrenze des Quarkradius bestimmt
werden. Abb. 8.17c zeigt wieder das Verhältnis zwischen Daten und Erwartung, wie in b), jetzt
für ZEUS Daten. Die durchgezogene Linie zeigt den Verlauf, welchen die Daten hätten, falls
Quarks einen Radius von 0.73 · 10−16 cm hätten. Aus den Daten kann ein Radius, der größer
als 0.73 · 10−16 cm wäre mit einer Wahrscheinlichkeit von 95% ausgeschlossen werden.
2
185
/dQ
2
−
e – p preliminary
1.15
Standard Model
1.1
CTEQ5D pdf
1
1.05
4
1
2
2
10
5
SM
√s=318 GeV
dσ/dQ / dσ
dσ/dQ (pb/GeV )
8.5 Die Suche nach Quarksubstruktur
-1
10
0.95
0.9
0.85
3
10
-2
3
10
-3
2
10
-4
10
1
H1
-5
10
10
2
10
3
10
2
0
4
10
3
10
2
4
2
Q (GeV )
2
Q (GeV )
ZEUS
N/NCTEQ5D
±
1.2
10
ZEUS (prel.) 94-00 e p
Rq=0.73 ⋅10
-16
1
10
3
10
4
cm
0.8
1
Quark Radius Limit
c)
b)
a)
10
3
10
4
Q2 [GeV2]
Abbildung 8.17: a)Wirkungsquerschnitt dσ/dQ als Funktion von Q2 aus Daten des H1Experiments. Die Kurve zeigt die Erwartung unter Annahme bestimmter Quark- und Gluonverteilungen (CTEQ5D). b) Das Verhältnis H1-Daten/Theorie. Die Daten stimmen im Rahmen
der Fehler bis zu den größten Werten von Q2 mit der Erwartung überein. c) Das Verhältnis von
Daten des ZEUS Experiments und der theoretischen Erwartung. Die Kurve zeigt die Erwartung für den Fall, daß die Quarks eine Ladungsverteilung mit einem Radius von 0.73 · 10−16 cm
hätten. Quarkradien größer als 0.73 · 10−16 cm können anhand der ZEUS Daten mit einer
Wahrscheinlichkeit von 95% ausgeschlossen werden.
2
186
Tiefunelastische Streuung: Struktur des Nukleons
Kapitel 9
Schwache Wechselwirkungen
Der Begriff ‘schwache Wechselwirkung’ wurde eingeführt, um die β–Zerfälle der Kerne zu beschreiben. Sie wurde zunächst nur an Zerfällen studiert. Von entscheidender Bedeutung waren
die Entdeckung der Paritätsverletzung in der schwachen Wechselwirkung und weiterhin der
Verletzung der Ladungskonjugation. Die bekannten Zerfälle konnten alle durch Austausch von
virtuellen W ± Bosonen hoher Masse erklärt werden. Als hochenergetische Neutrinostrahlen gebaut werden konnten, wurde eine neue Klasse von Studien möglich: Streuexperimente, die nur
über schwache Wechselwirkung ablaufen. In solchen Streuexperimenten wurde dann die neutrale
schwache Wechselwirkung entdeckt, die durch Austausch eines Z 0 Bosons beschrieben werden
kann. Solche Z 0 Bosonen waren schon 1967 in einer Klasse von sTheorien gefordert worden,
die “Eichtheorien” genannt wurden. Die Entdeckung der neutralen schwachen Wechselwirkung
im Jahre 1973 leitete den Triumph dieser Art theoretischer Beschreibung ein. Die Eichbosonen wurden 10 Jahre später erstmals experimentell nachgewiesen. Seither sind sie Gegenstand
intensiver Untersuchungen.
Wiederholung und Zusammenfassung von Eigenschaften der schwachen Wechselwirkung, die wir bisher kennengelernt haben.
• Die schwache Wechselwirkung wirkt auf alle Fermionen:
νe
e−
u
d
νµ
µ−
c
s
ντ
τ−
t
b
• Neutrinos haben NUR schwache Wechselwirkung.
• Die kurze Reichweite der schwachen Wechselwirkung läßt vermuten, daß Austauschteilchen schwer sind.
• Schwache Prozesse sind gekennzeichnet durch niedrige Wirkungsquerschnitte und lange
Lebensdauern.
• Einige Erhaltungssätze gelten nicht: Parität (z.B. Zerfall von
(neutrale Kaonen, B-Mesonen), Flavour (Strangeness)
60
Co, π ± ), C Parität, CP
188
Schwache Wechselwirkungen
• Paritätsverletzung wirkt sich auf die in schwachen Prozessen erlaubte Helizität aus (z.B.
ν haben λ = −1, ν haben λ = +1).
9.1
Zerfall des Pions und Struktur der schwachen Wechselwirkung
Die Entdeckung, daß in schwacher Wechselwirkung Parität und auch C-Parität verletzt sind hat
nicht nur die Gemüter erregt: man mußte auch sehen, wie man die Eigenschaften beschreiben
kann. Die elektromagnetische Wechselwirkung verletzt die Parität nicht, der elektromagnetische Strom der geladenen Teilchen kann durch einen Vektor beschrieben werden (ähnlich dem
Stromdichtevektor). Um die Paritätsverletzung in schwacher Wechselwirkung zu beschreiben,
geht man von einem ‘schwachen’ Strom aus, der aber kompliziertere Eigenschaften haben muss.
e-
νe
γ
W−
e−
e-
Die Wechselwirkung soll durch Austausch von W ± stattfinden also muß sich die Ladung ändern,
z.B. geht ein e− in ein νe über. Man spricht von einem ’geladenen’ Strom (engl. charged current). Es stellte sich durch viele Experimente heraus, daß zusätzlich zu einem Vektoranteil ein
Achsialvektoranteil notwendig ist, diese Theorie der schwachen Wechselwirkung wird deshalb
auch V − A Theorie genannt.
Ein experimenteller Befund wird nur mit der V − A Theorie richtig erklärt: der bereits in
Abschnitt 4.6 erwähnte Pionzerfall. Dort interessierte uns nur die Tatsache, daß die Parität im
Zerfall verletzt ist. Hier interessieren uns die Zerfallsmöglichkeiten.
Es gilt für die Verzweigungsverhältnisse im π Zerfall:
π + → µ+ νµ
π + → e + νe
99.9877%
1.23 · 10−4
(9.1)
(9.2)
Der Zerfall in e+ ist also stark unterdrückt. Warum? Die Leptonuniversalität sagt, daß die Kopplung des W ± an alle Leptonen gleich ist. Die Erklärung wird von der V − A Theorie geliefert.
Diese verlangt, daß Leptonen linkshändig an das W ± koppeln und Antileptonen rechtshändig.
Um das zu verstehen, erinnern wir uns an den Begriff der Helizität, den wir jetzt etwas
präzisieren wollen.
Der Helizitätsoperator ist definiert als:
Λ̂ =
~σˆ · p~ˆ
E|~σ |
(9.3)
9.1 Zerfall des Pions und Struktur der schwachen Wechselwirkung
189
Abbildung 9.1: Die Polarisation P von Elektronen, die in Kern β Zerfall beobachtet werden als
Funktion der Geschwindigkeit β = v/c.
~σˆ sind die Paulimatrizen, d.h. der Operator projiziert den Spin auf die Flugrichtung des Teilchens. Wenn der Spin entgegengesetzt zur Flugrichtung steht, so ist der Wert der rechten Seite
negativ, wenn |~
p| = E gilt, so gilt für den Eigenwert λ = −1. Wir hatten in Abschnitt 4.6
gesehen, daß das für Neutrinos gilt (z.B. Goldhaber Experiment). Antineutrinos haben λ = +1.
Massebehaftete Teilchen sind keine Eigenzustände zum Helizitätsoperator. Man kann jedoch
den Erwartungswert bestimmen.
Für Elektronen (Positronen) hatte man experimentell gefunden (s. Abb. 9.1 und Gl. 4.41, daß
sie polarisiert sind (gerechnet wird das nächstes Semester):
I+ − I −
P =
=
I+ + I −
(
+β
−β
für e+ , µ+ , (Antiteilchen)
für e− , µ− , (Teilchen)
(9.4)
wobei β = v/c und I+ und I− die Intensitäten für p~ parallel bzw. antiparallel zu ~σ sind.
Drehimpulserhaltung fordert im Zerfall des π + , daß das positiv geladene Lepton den Spin
entgegengesetzt zur Flugrichtung hat, genau wie das Neutrino. Die Wahrscheinlichkeit dafür
können wir aus Gl. 9.4 berechnen:
1−β
I−
=
−−→ 0
β→1
I+ + I −
2
(9.5)
Die entsprechende Wahrscheinlichkeit für ein positiv geladenes Lepton, seinen Spin parallel zur
Flugrichtung zu haben, ist nach Gl. 9.4:
1+β
I+
=
−−→ 1
β→1
I+ + I −
2
(9.6)
190
Schwache Wechselwirkungen
Jetzt sehen wir, was damit gemeint ist, daß in schwacher Wechselwirkung Leptonen linkshändig
und Antileptonen rechtshändig koppeln. Fermionen haben vorzugsweise den Spin antiparallel zur Flugrichtung. Der Grad der Ausrichtung hängt von der Geschwindigkeit ab. Bei β = 1 (masselose Teilchen) ist er 100%.
Für Antifermionen gilt entsprechendes: sie haben vorzugsweise den Spin parallel zur Flugrichtung.
Um einen numerischen Vergleich für den Zerfall des Pions in µ+ und e+ zu machen, müssen
wir für beide Fälle β berechnen. Mit Hilfe einer Beziehung aus der relativistischen Kinematik
bekommen wir:
m2π − m2µ
= 30 MeV/c
2mπ
m2π − m2e
= 70 MeV/c
=
2mπ
pµ =
pe
pµ
30 MeV
= 0.29 = 1 − 0.71
= √
Eµ
302 + 1042 MeV
70
pe
= √
= 1 − 2.7 · 10−5
βe =
Ee
702 + 0.5112
βµ =
Wir sehen, daß das Zerfallspositron nahezu Lichtgeschwindigkeit hat und damit die Wahrscheinlichkeit, seinen Spin entgegengesetzt zur Flugrichtung zu haben, nach Gl. 9.5 praktisch 0 ist.
Für das schwerere Myon kommt dagegen eine Wahrscheinlichkeit von 20% heraus.
Insgesamt ergibt sich für das Verhältnis der Quadrate der Matrixelemente:
|Mπ→µνµ |2
|Mπ→eνe
|2
=
1 − βµ
1 − βe
(9.7)
Um zum Verhältnis der Zerfallsbreiten zu kommen, muß noch der Phasenraumfaktor berücksichtigt
werden. Dieser ist:
ρ=
dN
d3 p
V
=
dE0
(2πh̄)3 dE0
=
dp
dE0
V
2 dp
4π
p
(2πh̄)3
dE0
(9.8)
bekommt man aus (der Index ` steht füer e oder µ):
q
E0 = mπ = Eν + E` = p + p2 + m2`
dp
=
p
dE0
2
m2π − m2`
2 mπ
2
m2π + m2`
2 m2π
Der Phasenraumfaktor ist also größer für den Zerfall in Elektron und Neutrino– wie zu erwarten.
Und es ergibt sich für das Verhältnis der Zerfallsraten:
9.2 Neutrinostrahlen und Entdeckung der neutralen schwachen Wechselwirkung
191
Abbildung 9.2: Positronspektren von gestoppten π + . Im rechten Teil sind die Positronen, die
direkt aus dem Pionzerfall stammen zu sehen (rechte y-Achse). Im linken Teil ist für den
π + → µ+ νµ das Positronenspektrum zu sehen, das aus dem µ+ Zerfall stammt.
m2µ (m2π − m2µ )2
1 − βµ p2µ dpµ
1
Γ(π + → µ+ νµ )
=
· 2
= 2 2
=
+
+
2
2
Γ(π → e νe )
1 − βe pe dpe
me (mπ − me )
1.282 · 10−4
Das experimentell gemessene Verhältnis ist oben bereits erwähnt worden, 1/1.23·10−4 . Es
stimmt also recht gut mit der einfachen Rechnung niedrigster Ordnung überein. In Abb.9.2
ist das Positronenspektrum aus π + Zerfällen zu sehen.
9.2
Neutrinostrahlen und Entdeckung der neutralen schwachen Wechselwirkung
Nach den Experimenten mit schwachen Zerfällen von Kernen wurden Experimente mit den
großen Flüssen von Neutrinos an Reaktoren durchgeführt. Z. B. gelang hier der erste Nachweis des Neutrinos (Reines, Cowan). Da die Neutrinos aus Reaktoren aber nur Energien von
einigen MeV haben und die Wirkungsquerschnitte proportional zur Neutrinoenergie sind, sind
die Reaktionsquerschnitte sehr klein. Hochenergetische Neutrinostrahlen wurden in den 1960er
Jahren erstmals gebaut. Sie werden an Protonensynchrotrons gemäß folgendem Schema gebaut
(Abb. 9.3):
• Möglichst viele hochenergetische Protonen auf ein Target schießen;
• Es entstehen viele hochenergetische Teilchen: vor allem π ± , auch π0 , K ± , etc.
• Zerfall der geladenen Pionen gemäß: π + → µ+ + νµ , π − → µ− + ν µ . Das geschieht in
einem langen evakuierten Zerfallstunnel.
• Impulsselektion der Hadronen durch Magnete vor dem Zerfallstunnel und Absorption der
Myonen (viel Absorber) dahinter.
192
Schwache Wechselwirkungen
Abbildung 9.3: Prinzipbild des Neutrinostrahls.
Läßt man diese Neutrinos nun auf einen Detektor fallen, der eine genügend große Masse hat, so
kann man ihre Wechselwirkungen untersuchen. Man hat 1973 am europäischen Forschungszentrum CERN in der Blasenkammer Gargamelle den ersten Nachweis der Existenz von neutralen
schwachen Strömen erbracht. Diese wurden durch Streuung am Elektron gefunden (sehr kleiner
Wirkungsquerschnitt!):
νµ + e − → ν µ + e −
ν µ + e− → ν µ + e− .
Die Signatur solcher Ereignisse ist ein einzelnes Elektron. Es war nicht leicht, sicher zu stellen,
daß es sich nicht um Untergrund handelte.
Das zugehörige Feynmandiagramm ist:
Zeit
6
e-
ν
Z
e-
µ
e-
0
ν
Z
νµ
0
e-
Häufiger tritt die Reaktion am Nukleon auf:
νµ + N → ν µ + X −
µ
ν µ + N → ν µ + X.
νµ
9.2 Neutrinostrahlen und Entdeckung der neutralen schwachen Wechselwirkung
ν
µ
X
Z
νµ
0
N
Man bezeichnet den Übergang ν → ν als “neutralen Strom”, dann ist der Übergang e− → νe
entsprechend ein “geladener Strom”. Das ist im Bosonaustauschbild natürlich äquivalent dem
Austausch von Z 0 und W ± . Mit νe und ν e sind auch Reaktionen des geladenen Stroms möglich:
Zeit
6
νe
eνe
W
e-
e-
W
ν
-
e
νe
e-
Bei Gargamelle wurde das Verhältnis der Ereignisse mit neutralen Strömen zu den geladenen
bestimmt:
N C 1
σ(νµ N → νµ X)
'
(9.9)
=
CC ν σ(νµ N → µ− X)
2
N C σ(ν µ N → ν µ X)
1
=
'
(9.10)
+
CC ν
σ(ν µ N → µ X)
4
Nach Untersuchung von Reaktionen der Neutrinos wurde es klar, warum es nicht möglich war,
die neutrale schwache Wechselwirkung in Zerfällen zu entdecken: Im Gegensatz zur geladenen
schwachen Wechselwirkung, bei der sich die Quarksorte ändert, oder ein geladenes Lepton in
ein Neutrino übergeht, gilt für neutrale schwache Wechselwirkung:
KEINE FLAVOURÄNDERUNG IN NEUTRALEN SCHWACHEN WECHSELWIRKUNGEN
Wenn aber die auffällige Signatur der Flavouränderung fehlt, z.B. ∆S = 1, so wird ein neutraler schwacher Prozeß in Zerfällen immer von einem elektromagnetischen oder gar starken
überdeckt werden. Erst als Neutrinos für Streuexperimente zur Verfügung standen, war die
Entdeckung möglich, da Neutrinos nur schwach wechselwirken. In ‘elektroschwachen’ Theorien,
193
194
Schwache Wechselwirkungen
die seit etwa Anfang der 1960er Jahre diskutiert wurden, hatte man solche schwachen neutralen
Wechselwirkungen erwartet.
9.3
Universalität der schwachen Wechselwirkung
9.3.1
Leptonuniversalität
Wenn man Prozesse wie die schwachen Zerfälle der µ und τ Leptonen tatsächlich durch W
Austausch beschreiben kann, so stellt sich natürlich sofort die Frage, ob die Kopplungsstärke
des W Bosons an alle Leptonen gleich ist. Beschreibt man die Kopplung des W an den `− − ν`
Vertex mit gW , so heißt die Frage: ist gW für alle Leptonen gleich und wie groß ist die Kopplung
an Quarks?
νµ
νe
W
ντ
−
W
−
W−
gW
gW
gW
e−
µ−
τ−
Abbildung 9.4: Übergänge `− → ν` + W − unter der Annahme der Leptonenuniversalität, d.h.
alle Vertizes werden durch ein und dieselbe Kopplungsstärke gW beschrieben.
Diese Hypothese kann man z.B. durch Vergleich folgender rein leptonischer Zerfälle nachprüfen:
µ− → e − ν e ν µ
τ − → e − ν e ντ
Man muß bei dem Vergleich die unterschiedlichen Massen der geladenen Leptonen berücksichtigen.
Weiterhin muß man beachten, daß das τ Lepton wegen seiner hohen Masse nicht nur in e− ν e ντ
sondern auch in µ− ν µ ντ und in ντ + Hadronen zerfällt. Das Verzweigungsverhältnis für den
oben angegebenen τ Zerfall in e− ν e ist 18%, ebenso für τ − → ντ µ− ν µ . Gut für Universalität!
Es soll jetzt das Verhältnis der Lebensdauern von τ und µ abgeschätzt werden, um die Hypothese der Universalität zu prüfen und zu verdeutlichen.
9.3 Universalität der schwachen Wechselwirkung
195
e−
νe
ντ (νµ )
gW
W
gW
τ − oder µ−
Benutzt man die oben eingeführte Kopplungsstärke gW für die Kopplung des W an Leptonen,
so ist das Matrixelement für µ− → e− ν e νµ bis auf Konstanten gegeben durch:
M (µ− → e− ν e νµ ) ∼
2
gW
2
MW
Die W Masse im Nenner ist eine Näherung für den W -Bosonpropagator, die für niedrige Impulsüberträge gilt:
1
1
| 2
| −−
−→ | 2 |
(9.11)
2
2
q − MW q →0 MW
Um die Übergangswahrscheinlichkeit zu erhalten, muß man noch den Phasenraumfaktor ρ
berücksichtigen. Man kann ihn durch eine Dimensionsbetrachtung abschätzen. Da die Zerfallsbreite Γ(µ− → e− ν e νµ ) ∼ |M|2 ist, käme als Dimension für Γ GeV−4 heraus, falls ρ
dimensionslos ist. Da die Dimension von Γ aber GeV ist, muß ein weiterer Faktor auftreten mit
Dimension GeV5 . Vernachlässigt man die Masse des Elektrons gegen die des Myons, so muß
sein Γ ∼ m5µ . Diese Abhängigkeit von der 5. Potenz der Myonmasse kommt bei einer genaueren
Rechnung auch heraus.
Zusammengefaßt:
g4
Γ(µ− → e− ν e νµ ) = k W4 m5µ .
MW
k ist eine Konstante. (Die exakte Formel ist in Gl. 9.12 zu sehen.) Vergleichen wir jetzt µ und
τ:
ττ
Γ(µ− → e− ν e νµ )
Γ(µ− → e− ν e νµ )
=
=
· BR (τ → e− ν e νµ )
−
τµ
Γ(τ → alles)
Γ(τ → e ν e νµ )
5
mµ
· BR (τ → e− ν e νe ) = 0.135 · 10−6
=
mτ
Die Messung bestätigt diese Erwartung: 0.132 · 10−6
196
Schwache Wechselwirkungen
9.3.2
Fermi-Kopplungskonstante
Aus historischen Gründen wird in schwachen Prozessen eine andere Nomenklatur gewählt, die
von Fermi eingeführt wurde. Z.B. schreibt man für den Myonzerfall:
G2F m5µ
(9.12)
Γµ =
192π 3
g4
(9.13)
von oben
Γµ = k W4 m5µ
MW
1
2
d.h. k =
·
(9.14)
3
192π 64
Hier ist GF die Fermi-Kopplungskonstante. Die Lebensdauer des Myons ist sehr genau vermessen. Daraus folgt der Bestwert für
GF = 1.1664 · 10−5 GeV−2 .
Der Fehler ist ∼ 10−6 des Wertes.
GF ist also dimensionsbehaftet. Im W Austauschbild kommt die Dimension durch den W
Propagator zustande, wie man aus Gl. 9.12 und 9.13 sieht:
√
2
2 gW
.
GF =
2
8 MW
2 2
In der Zerfallsbreite hat man also (gW
) oder G2F . Man kann die Kopplungsstärke gW mit der
elektromagnetischen vergleichen:
s
√
8GF
√ ' 0.6
ge = e = 4πα ' 0.3 gW = MW
2
gW und ge sind also von gleicher Größenordnung. Die Schwäche der schwachen Prozesse liegt
nicht an der schwachen Kopplung, sondern an der hohen Masse der Austauschteilchen, die im
Propagator auftaucht.
Erinnern wir uns, daß wir im Propagator eine Vernachlässigung gemacht haben, Gl. 9.11, die
nur für niedrige |q 2 | gültig ist. In der Tat hat man bei HERA verifiziert, daß oberhalb von
|q 2 | ' 10000 GeV2 der Wirkungsquerschnitt e− p → e− X (Austausch neutraler Bosonen, γ und
Z 0 ) und der für e− p → νe X (Austausch von W ± ) in etwa gleich sind.
9.3.3
Schwache Wechselwirkung von Quarks
Besonders interessant sind die schwachen Wechselwirkungen der Quarks. Die geladenen Feldquanten W ± ändern die Quarksorte. Ein u-Quark kann in ein d- oder s-Quark übergehen und
dabei ein (virtuelles) W + emittieren. Das gleiche trifft auf das c-Quark zu.
Beispiele sind: n → pe− ν e , wobei ein Elementarprozeß d → u + W − vorkommt. Bei Λ → pe− ν e
haben wir als Elementarprozeß: s → u + W − oder bei D − → K 0 e− ν e ist der Elementarprozeß
c → s + W −.
Wie man in den Diagrammen sieht, benutzt man das “Zuschauermodell”: Ein Quark ist an der
schwachen Wechselwirkung beteiligt, die andern “schauen zu”. Die Frage ist wieder: gilt hier
immer noch Universalität? Eine gute Näherung ist tatsächlich:
gW ' gud ' gcs
9.3 Universalität der schwachen Wechselwirkung
dd
e−
udu
e
νe
νµ
W
gW
197
−
ds
e
νe
−
W
gW
gud
e−
νe
W
gW
gud
νe
gW
gcs
W
gW
du
µ
−
udd
0 −
π → π e νe
dc
−
−
D → K 0 e− ν e
n → p e νe
gud bezeichnet die W Kopplung an das Quark beim Übergang u → dW + . Für Übergänge
zwischen Quarks in ein und derselben Familie ist die Kopplung des W Bosons in etwa gleich
der bei den Leptonen. Anders ist es bei Übergängen zwischen den Familien:
u↔s
oder
c↔d
In der Formulierung von Cabibbo werden die Beobachtungen elegant durch folgenden Trick
beschrieben. Es sind nicht die d- und s-Quarks, die an der schwachen Wechselwirkung durch
W -Austausch teilhaben, sondern Mischzustände der beiden Quarks:
d0 = d cosθC + s sinθC
s0 = −d sinθC + s cosθC
(9.15)
(9.16)
θC ist der Cabibbo-Winkel. Man wählte diese Parametrisierung, als die dritte Familie noch
nicht bekannt war. In Wahrheit ist auch noch das b-Quark hinzugemischt. Dies wird durch die
Cabibbo-Kobayashi-Maskawa-Matrix beschrieben, auf die wir weiter unten kommen.
Die Basiszustände für die schwache Wechselwirkung sind “rotiert” gegen die für die starke
Wechselwirkung wichtigen Zustände. Die Quarkdubletts, die symmetrisch zu den Leptondubletts sind, sind die mit den gemischten Zuständen d0 und s0 :
µ
c
d0
s0
Das W Boson vermittelt Übergänge
u ↔ d0
oder
c ↔ s0 .
Damit kann das u in d und in s übergehen, nur ist die Wahrscheinlichkeit unterschiedlich. Es
kommt der entsprechende Faktor des rotierten Zustandes hinzu. Der Übergang u ↔ s ist also
unterdrückt gegenüber dem u ↔ d, die Amplituden sind:
µ+ → ν µ W + ∼ g W
u → d W+
∼ gW cosθC
+
u → sW
∼ gW sinθC
198
Schwache Wechselwirkungen
Mit Hilfe der Quark-Mischung kann man die Zerfälle der geladenen K und π Mesonen in ein
Myon und ein Neutrino erklären:
2
Γ(π + → µ+ νµ ) ∼ gW
cos2 θC
2
Γ(K + → µ+ νµ ) ∼ gW
sin2 θC
νµ
µ−
gW
νµ
µ−
gW
W−
gud
gus
u
d
π
W−
u
s
−
K
−
2
gW
sin2 θC
Γ(K + → µ+ νµ )
sin2 θC
∼
∼
2
Γ(π + → µ+ νµ )
gW
cos2 θC
cos2 θC
Aus Messungen dieser und anderer Reaktionen bestimmt man den Cabibbo Winkel. Nach Anbringen von Phasenraumkorrekturen, die die unterschiedlichen Massen von K und π berücksichtigen,
kommt heraus:
sin θC = 0.220 ± 0.003
θC = 12.7◦ ± 0.1◦
Die Cabibbotheorie erklärt, warum Übergänge mit ∆S = 0 stark bevorzugt sind:
d ↔ u ∼ cos2 θC
s ↔ u ∼ sin2 θC
Cabibbo erlaubt
Cabibbo unterdrückt
Z.B. kommt für das Verhältnis von Neutronzerfall zu Myonzerfall heraus:
2
Γ(n → p e− ν e )
gud
∼
' cos2 θC = 0.95.
2
Γ(µ− → e− ν e νµ
gW
Zerfälle des Charmquarks Bei den Zerfällen von Mesonen mit Charmquarks gelten analoge
Überlegungen:
Γ(D 0 → K − e+ νe ) ∼ gcs = gW cos θC ,
da das D 0 ein c Quark enthält, welches in ein s Quark übergeht. Und weiter:
Γ(D 0 → π − e+ νe ) ∼ gcd = gW sin θC ,
9.4 Die Z 0 und W ± Bosonen
199
hier geht das c Quark in ein d quark über. Das Verhältnis ist 20:1, die meisten c Quarks gehen
in ein s über.
Bei den Quarkkopllungen an das Z 0 Boson, stellt sich die Frage: sind d0 d0 oder s0 s0 zu nehmen?
Z 0 → d0 d0 + s0 s0 = dd cos2 θC + ss sin2 θC + ds cos θC sin θC + sd cos θC sin θC
+ dd sin2 θC + dd cos2 θC − ds cos θC sin θC − sd cos θC sin θC
= dd + ss
(9.17)
(9.18)
(9.19)
Die erste Zeile stammt von d0 d0 , die zweite von s0 s0 . Man sieht zweierlei:
1. Die Übergänge mit ∆S 6= 0 heben sich heraus. Die Regel über die Nicht-Existenz von
flavourändernden neutralen Strömen findet dadurch eine Erklärung.
2. Es ist gleich, ob man die ‘rotierten’ oder die unrotierten Zustände nimmt. Letzteres ist
das Übliche.
Historische Anmerkung: Als die Überlegungen über neutrale Ströme gemacht wurden (ca 1970),
war das Charmquark noch nicht gefunden worden. Glashow, Iliopoulos und Maiani postulierten es, um zu erklären, warum der Übergang K 0 → µ+ µ− nur ein Verzweigungsverhältnis von
∼ 10−9 hat. K 0 → Z 0 → µ+ µ− geht nicht nach 9.19. Der Übergang über ein Diagramm mit
zweifachem W Austausch lieferte einen viel zu großen Wert, falls nur das linke Diagramm
mit s → W u beiträgt. Das von Glashow, Iliopoulos und Maiani postulierte c Quark liefert Beiträge mit anderem Vorzeichen und führt zu einer fast vollständigen Auslöschung der
Übergangsamplitude.
0
0
K
K
d
d
s
s
Zeit
6
u
u
c
W
d
W
s
K0
9.4
c
d
s
K0
Die Z 0 und W ± Bosonen
Nach den ersten Neutrinoexperimenten und der Entdeckung und Messung der neutralen schwachen Wechselwirkung hat man die elektroschwache Theorie ernst genommen. Diese konnte die
Massen und Zerfalls–Charakteristika der Vektorbosonen W ± und Z 0 vorhersagen.
200
Schwache Wechselwirkungen
9.4.1
Entdeckung der Z 0 und W ± Bosonen
Die schwachen Austauschbosonen wurden 10 Jahre nach der Entdeckung der neutralen schwachen Wechselwirkung im Jahre 1983 in pp Kollisionen am CERN entdeckt. Es handelte sich
um eine ‘geplante’ Entdeckung. Eigens dafür war ein bestehendes Synchrotron, das SPS (Super
Proton Synchrotron) in einen Speicherring umgebaut worden, welches ‘SppS’ getauft wurde.
Die pp Schwerpunktenergie war 540 GeV.
Zeit
e+
6
f
W
-+
Z
oder
q
νe
+
e
e-
f’
0
W
+
Z0
q
p
p
u
d
u
u
Unter den Zerfallsarten sollten die leptonischen Zerfälle W → l + νl , Z 0 → ll und Z 0 →
νl ν l (wobei l = e, µ, τ ) vorkommen, sowie die zahlreicheren Zerfälle in Hadronen, die über
Quarkpaare gehen, W, Z → qq → Hadronen.
Die Elementarprozesse für Produktion und leptonischen Zerfall sind:
u + d → W + → e+ + νe ,
oder µ+ + νµ ,
oder τ + + ντ
(9.20)
u + d → W − → e− + ν e ,
oder µ− + ν µ ,
oder τ − + ν τ
(9.21)
oder τ + τ −
(9.22)
u+u
d+d
→ Z 0 → e + e− ,
oder µ+ µ− ,
Der Wirkungsquerschnitt für Reaktion (9.20), die Produktion eines W Bosons in Ruhe im
Schwerpunktsystem und nachfolgender leptonischer Zerfall, wird von der Breit–Wigner Formel
(hier nicht-relativistische Näherung) beschrieben:
Γud Γeν
σ(ud → W + → e+ νe ) ∼ √
( ŝ − MW )2 + Γ2 /4
(9.23)
ŝ ist das Quadrat der Schwerpunktenergie des ud Systems. Γ, Γud , Γeν sind die totalen und
partiellen Zerfallsbreiten. Zusätzlich zu der Energieabhängigkeit muß man bei der Berechnung
des Wirkungsquerschnitts noch Faktoren für die Spins der Quarks und des Bosons sowie für die
Farben und auch die Cabibbo Winkel berücksichtigen. Der Wirkungsquerschnitt am Maximum
ŝ = MW ist dann:
σmax (ud → W + → e+ νe ) =
4π
4π Γud Γeν
=
= 9.2 nb,
2
2
3MW
Γ2
81MW
(9.24)
wobei der Wert MW = 80 GeV eingesetzt wurde.
Falls Da W ± in Quarks zerfällt, W → ud, W → cs, so muß man wieder einen Faktor 3 für
Farbe berücksichtigen, während der Zerfall in das dritte Quarkpaar tb wegen Energieerhaltung
9.4 Die Z 0 und W ± Bosonen
201
nicht erlaubt ist. Jeder Zerfall W → eνe , µνµ , τ ντ hat das Gewicht 1, so daß Γud /Γ =
Γeν /Γ = 19 .
1
3
und
Der Wirkungsquerschnitt für Z  Produktion nach (9.22) hängt zusätzlich vom schwachen Mischungswinkel sin2 θW ab, der später diskutiert wird. Es stellt sich heraus, daß der Wirkungquerschnitt um einen Faktor 10 kleiner ist als der für W Produktion.
Die Wirkungsquerschnitte für die Reaktionen pp → W + + . . . mit anschließendem Zerfall
W + → e+ ν und pp → Z 0 + . . . mit Z 0 → e+ e− ergeben sich durch Integration des elementaren
Quark–Wirkungsquerschnitts (9.23) über die Breite des Bosons und die Impulsverteilungen
der Quarks im Nukleon. Für 270 GeV Protonen und Antiprotonen, die 1983 in den ersten
Experimenten am CERN pp Speicherring verwendet wurden, sind sie von der Größenordnung
σ(pp → W → eν) ∼ 1 nb
und
σ(pp → Z 0 → e+ e− ) ∼ 0.1 nb.
Diese Werte müssen mit dem Wert σtot = 40 mb = 4 · 107 nb für den totalen pp Wirkungsquerschnitt verglichen werden.
Es war nur möglich, solch seltenen Ereignisse, etwa 10−8 −10−9 der Gesamtzahl, zu messen, weil
Elektronen, Myonen und Neutrinos aus den W und Z Zerfällen sehr hohe Transversalimpulse
haben, pT bis zu MW /2 ' 40 GeV/c. Andere Leptonen, zum Beispiel aus Hadronzerfällen,
weisen viel kleinere pT Werte auf.
Die Detektoren, die in den Experimenten (UA1, UA2) verwendet wurden, bestanden aus zentralen Spurenkammern zum Nachweis der Sekundärteilchen, die von einem elektromagnetischen
Kalorimeter umschlossen waren (zum Nachweis von elektromagnetischen Schauern aus Elektronen und Photonen), einem viel größeren Kalorimeter, das für die Messung von Hadronenjets benutzt wurde und einem externen Myondetektor. Die Kalorimeter waren in Polar– und
Azimutal–Winkel θ und φ segmentiert.
Abb. 9.5 zeigt die Rekonstruktion eines typischen W → eν Ereignisses. Charakteristisch ist:
(i) ein Elektron mit hohem pT , das als eine einzelne isolierte Spur von hohem Impuls im
zentralen Spurendetektor auftritt und auf einen Schauer (ii) zeigt;
(ii) ein kompakter Schauer im elektromagnetischen Kalorimeter ohne signifikante Energie–
Ablagerung in den nahe gelegenen Kalorimetersegmenten, und
(iii) das “Fehlen” von Transversalimpuls, wenn man für alle Sekundärteilchen den Transversalimpuls aufsummiert. Diese Sekundärteilchen stammen aus der Hadronisierung der anderen Quarks, die in der Kollision auftreten, und haben zumeist niedriges pT . Das Fehlen
von pT wird auf das Neutrino aus dem W –Zerfall zurückgeführt.
Abb. 9.6 stellt den fehlenden Transversalimpuls im Vergleich zum gemessenen Transversalimpuls des Elektrons dar. Sie sind im Rahmen der Fehler gleich. Bei der Analyse zeigt sich, daß
der Transversalimpuls des Elektrons zeigt in in die entgegengesetzte Richtung des fehlenden
Transversalimpulses zeigt, wie erwartet.
Ebenso werden Zerfälle in Myonen W → µν, Z 0 → µ+ µ− beobachtet, wobei gefordert wird, daß
ein (oder zwei) Teilchen mit hohem pT das Hadron Kalorimeter durchdringen (welches ungefähr
sechs Wechselwirkungslängen hat) und in den äußeren Myonkammern nachgewiesen werden.
202
Schwache Wechselwirkungen
Abbildung 9.5: W − → e− + ν̄e Ereignis aufgenommen mit dem UA1 Detektor am SppS (CERN).
Alle Spuren und getroffenen Kalorimeterelemente sind dargestellt. Unten wurde zusätzlich die
Forderung gestellt, daß nur Teilchen mit pT > 1 GeV/c und Kalorimeterelemente mit ET > 1
GeV gezeigt werden.
9.4 Die Z 0 und W ± Bosonen
203
Abbildung 9.6: Links: Fehlender Transversalimpuls gegen gemessenen Transversalimpuls des
Elektrons in Kandidatenereignisse für W Bosonen. Rechts: Winkelverteilung für Elektronen in
W Ereignissen, θ ∗ ist der Elektronwinkel relativ zum Proton.
9.4.2
Paritätsverletzung beim W Zerfall
In folgender Skizze sieht man, daß das W − in Kollisionen von Quark und Antiquark, die an
schwacher Wechselwirkung nur mit Helizität -1 und 1 teilnehmen, polarisiert ist: sein Spin zeigt
in Richtung des einfliegenden Antiprotons.
d
u
u
d
+
W
W
Im W − Zerfall hat man folgende Helizitäten:
W
νe
e
-
Man erwartet daher, die Zerfallselektronen bevorzugt entgegengesetzt zur z Komponente des
W − Spins, dh. in Protonrichtung zu messen. Ebenso erwartet man, e+ vorzugsweise in Antiprotonrichtung zu messen.
204
Schwache Wechselwirkungen
Abbildung 9.7: Z 0 → e− + e+ Ereignis aufgenommen wie in Abb. 9.5. Alle Spuren und getroffenen Kalorimeterelemente sind dargestellt, Unten mit der Forderung, daß Teilchen mit pT > 2
GeV/c und Kalorimeterelemente mit ET > 2 GeV gezeigt werden. Schnitt in Abb. ist falsch.
9.4 Die Z 0 und W ± Bosonen
205
Abbildung 9.8: Invariante Masse von hochenergetischen µ+ µ− und e+ e− Paaren in pp Wechselwirkungen aufgenommen mit dem CDF Detektor am pp Speicherring Tevatron.
e-
θ
p
ν
∗
p
e
Die Winkelverteilung im Ruhesystem ist leicht zu messen. In Abb. 9.6 ist rechts die gemessene
Winkelverteilung für Elektronen aufgetragen, wobei θ ∗ relativ zum Proton gemessen wird. Man
sieht, daß das Elektron in der Tat bevorzugt bei kleinen Streuwinkeln auftritt.
9.4.3
Präzisionsvermessung des W Bosons
Nach der glanzvollen Bestätigung der Vorhersagen der “elektroschwachen Theorie”, in der die
elektromagnetische und die schwache Wechselwirkung durch Austausch von Bosonen beschrieben werden, ging man daran, sie genauer zu untersuchen. Dazu wurden W und Z Bosonen mit
hoher Statistik an Speicherringen erzeugt und ihre Parameter, also Massen und Breiten, genau
bestimmt. Die elektroschwache Theorie wurde jetzt zu einem Teil des sogenannten “Standard
Modells”.
206
Schwache Wechselwirkungen
Speicherring
Tevatron
LEP I
SLC
LEP II
Standort
Fermilab, Chicago
CERN, Genf
SLAC, Stanford
CERN, Genf
Typ
pp
e + e−
e + e−
e + e−
√
s[GeV]
1800
MZ
MZ
208
Die elementaren Zerfälle des W + Bosons sind im Standard Modell (für W − gilt entsprechendes):
W + → e + νe
→ µ+ νµ
→ τ + ντ
→ ud0
→ cs0
Dabei sind die Zerfälle in b Quarks mit enthalten, s. später im Kapitel über schwache Wechselwirkung der Quarks. Zerfälle in t Quarks sind nicht möglich. Das W Boson wird am Tevatron
in pp Kollisionen untersucht, sehr ähnlich wie im vorigen Abschnitt bei deren Entdeckung beschrieben. Man kann seine Masse durch Auftragen des Transversalimpulses des Zerfallsleptons,
oder durch Auftragen der transversalen Masse bestimmen: Falls das W Boson ohne Transversalimpuls zur Strahlachse erzeugt wird, ist der Transversalimpuls des Zerfallsleptons:
p`t =
MW
· sinθ,
2
wobei θ der Winkel des Leptons zur Strahlachse ist. Die Verteilung zeigt ein Maximum bei
MW /2 (Jacobi Peak, s. Übungsaufgabe).
Zur Erläuterung der transversalen Masse sei folgendes bemerkt. Normalerweise würde man die
invariante Masse des W Bosons rekonstruieren nach:
m2W = (Pe + Pν )2 = (Ee + Eν )2 − (p~e + p~ν )2
Das Problem ist aber, daß das Neutrino aus dem W Zerfall “unsichtbar” ist. Man kann aber
den “fehlenden Transversalimpuls” bestimmen, indem man alle gemessenen Transversalimpulse
vektoriell addiert und die Komponenten mit negativem Vorzeichen versieht. Nimmt man an,
daß der fehlende Transversalimpuls hauptsächlich durch das Neutrino verursacht wird, so kann
man die transversale Masse definieren:
m2T = (Ee + Eν )2 − (p~T e + p~T ν )2
(9.25)
In Abb. 9.12 ist die transversale Masse gemessen von der CDF Kollaboration am TEVATRON
aufgetragen. Man sieht wieder ein Maximum bei der halben W Masse. Durch Anpassen dieser
Verteilung bekommt man eine sehr genaue Massenbestimmung für das W :
MW = (80.47 ± 0.06) GeV
ΓW = (2.11 ± 0.28) GeV
# Events
9.4 Die Z 0 und W ± Bosonen
207
2000
CDF(1B) Preliminary
W→eν
1500
χ /df = 82.6/70 (50 < MT < 120)
2
χ /df = 32.4/35 (65 < MT < 100)
Mw = 80.473 +/- 0.065 (stat) GeV
2
Backgrounds
1000
KS(prob) = 16%
500
Fit region
0
50
60
70
80
90
100
110
120
Transverse Mass (GeV)
Abbildung 9.12: Transversale Masse mT gemessen durch das CDF Experiment am pp Speicherring Tevatron.
Beim Speicherring LEP II können W + W − Paare paarweise erzeugt
werden, e+ e− → W + W − .
√
Dafür mußte die Schwerpunktsenergie des Speicherrings
auf s ≥ 2 · MW gesteigert werden.
√
Messungen an der Schwelle, d.h. im Bereich 161 ≤ s ≤ 180 GeV ergeben:
MW = (80.4 ± 0.21) GeV.
Rekonstruktion der Zerfallsprodukte lieferte eine weitere Messung der Masse:
e+ e− → W + W −
qq qq
→ qq `ν
`ν `ν
Man hat durch Vermessung von Ereignissen mit 4 Jets bekommen:
MW = (80.450 ± 0.039) GeV
ΓW = (2.15 ± 0.091) GeV
Weltbestwert (2000): MW = (80.451 ± 0.033) GeV. Immerhin entspricht das schon einem Fehler
von nur 0.0004 des Wertes.
9.4.4
Z 0 Produktion an e+ e− Speicherringen
Nachdem 1983 W und Z Bosonen am CERN pp Speicherring erstmals beobachtet wurden,
wurde das Z Boson ab 1989 als Resonanz in e+ e− Kollisionen am LEP (CERN, Genf) und
am SLC (SLAC, Stanford) beobachtet. Abb.√(8.15) zeigt das Z 0 als e+ e− Resonanz bei der
entsprechenden Schwerpunktenergie Energie s ' MZ .
Das Z 0 als schwaches Austauschboson zerfällt in alle fundamentalen Fermionen (außer t Quarks,
208
Schwache Wechselwirkungen
02/03/2001
LEP
Preliminary
15
σ
WW
[pb]
20
10
RacoonWW / YFSWW 1.14
no ZWW vertex (Gentle 2.1)
only νe exchange (Gentle 2.1)
5
0
160
170
180
190
200
210
Ecm [GeV]
Events / 2 GeV/c
2
Abbildung 9.16: Messung von W + W − an der Schwelle in e+ e− Wechelwirkungen bei LEP II.
350
data 192-202 GeV
WW (mW = 80.35)
300
ZZ
250
–
qq(γ)
DELPHI preliminary
200
150
100
50
0
50
55
60
65
70
75
80
85
90
95
100
2
W mass (GeV/c )
Abbildung 9.17: Rekonstruktion der W Masse in 4-Jet Ereignissen im Detektor DELPHI bei
LEP II.
9.4 Die Z 0 und W ± Bosonen
209
die zu schwer sind):
Z 0 → e + e−
→ µ + µ−
→ τ +τ −
→
→
→
→
→
uu
dd
cc
ss
bb
→ νe ν e
→ νµ ν µ
→ ντ ν τ
Die partiellen Zerfallsbreiten sind grob:
Γlepton = Γ(Z 0 → e+ e− ) + Γ(Z 0 → µ+ µ− ) + Γ(Z 0 → τ + τ − ) ∼ 10%
X
Γhad =
Γ(Z 0 → qi q i ) ∼ 70%
i
Die Quarkzerfälle sind meßbar als Z 0 → Hadronen. Die experimentelle Unterscheidung der
Quarksorten bedarf erheblicher Anstrengung und ist nicht immer möglich. Ereignisse mit c und
mit b Quarks kann man recht gut unterscheiden, s. unten bei der Entdeckung des Top Quarks.
Die Zerfälle in Neutrinos sind im Detektor unsichtbar und sollten den Rest ausmachen, also
∼ 20%.
Der Wirkungsquerschnitt für e+ e− → Z 0 → f f ist:
σ=
12 π Γee Γf f
s
,
2
2 2
MZ
(s − MZ ) + s2 Γ2 /MZ2
(9.26)
Γ ist die totale Breite des Z 0 , Γee die partielle Breite für den Zerfall Z 0 → e+ e− und Γf f für
den Zerfall Z 0 → f f . Es gibt auch nichtresonante Beiträge zum Wirkungsquerschnitt durch
Austausch von Photonen und Interferenz von Photon und Z 0 , aber diese sind klein und werden
hier vernachlässigt.
Somit gilt beim Resonanzmaximum:
12π Γee Γf f
+ −
0
σmax (e e → Z → f f ) = 2
.
(9.27)
MZ
Γ2
Der Wirkungsquerschnitt für die punktförmige, nichtresonante Reaktion e+ e− → µ+ µ− durch
Einphoton–Austausch ist:
σpunkt =
4πα2
,
3s
Somit erwarten wir für s = MZ2
9
σmax (e+ e− → Z 0 → µ+ µ− )
= 2
R=
σpunkt
α
Γee Γµµ
Γ2
.
(9.28)
210
Schwache Wechselwirkungen
Cross-section (nb)
Cross-section (nb)
Hier wurden die Massen mµ , me im Vergleich mit MZ vernachlässigt. Γee /Γ ' Γµµ /Γ ' 0.034,
was R ' 195 ergibt. Dieser Wert gilt vor Berücksichtigung radiativer Korrekturen, die ihn
auf R ' 150 reduzieren. Diese Korrekturen, die durch Abstrahlung im Ausgangszustand e+
und e− auftreten, reduzieren nicht nur den Maximalwert, sondern verzerren auch die Form der
Resonanzkurve.
Bei LEP wurden in der sogenannten Phase I (d.h. bei der Energie der Z Masse) von 4 Experimenten (ALEPH, DELPHI, L3, OPAL) ungefähr 16 Millionen Zerfälle Z 0 → Hadronen
registriert. Es war möglich damit hochpräzise Messungen zu machen. Benutzt wurden alle
“sichtbaren” Zerfälle, Z 0 → f f , wobei f = e− , µ− , τ − , und u, d, c, s, b ist. Erzeugung von top
Quarks ist nicht möglich.
Die Breit-Wignerverteilungen (Beispiele in Abb.9.18) werden durch Messungen bei verschiedenen Strahlenergien gemacht. Es ist eine genaue Kenntnis der Strahlenergie notwendig, um die
letztendlich erreichte Präzision zu bekommen.
Die Masse und totale Breite des Z  wird durch eine Anpassung an die gemessenen Resonanz35
1990
1991
1992
1993
1994
1995
hadrons
30
25
20
OPAL
1.2
+ -
ee
1
s+t
s
non-s
0.8
0.6
15
0.4
10
0.2
5
0
88
89
90
91
92
93
94
data/fit - 1
0
Cross-section (nb)
-0.01
89.4
89.5
91.2
91.3
92.9
93
µµ
+ -
1.6
1.4
1.2
90
91
92
93
91.2
91.3
92.9
91
92
93
91.2
91.3
92.9
94
95
93
93.1
94
95
93
93.1
√s(GeV)
1
1.2
1
0.6
0.4
0.4
0.2
0.2
90
91
92
93
94
0
95
√s(GeV)
88
89
90
√s(GeV)
0.05
data/fit - 1
0.05
+ -
1.4
0.6
89
89.5
ττ
1.6
0.8
88
89.4
1.8
0.8
0
-0.05
89
0
-0.05
93.1
1.8
0
88
0.05
Cross-section (nb)
data/fit - 1
0.01
data/fit - 1
0
95
√s(GeV)
89.4
89.5
91.2
91.3
92.9
93
0
-0.05
93.1
89.4
89.5
Abbildung 9.18: Der Wirkungsquerschnitt σ(e+ e− → Z 0 → f f ), als Funktion der Schwer21: The measured
cross-sections
for hadronic andmit
leptonic
final states as a function
of centre-of- wieder und
punktsenergie. Figure
Die Kurven
geben
die Anpassungen
Breit–Wigner
Verteilungen
mass energy. The errors shown are statistical only. The solid line is the result of the 9-parameter modelschließen die Auswirkungen
der
radiativen
Korrekturen
mit ein,
was lepton
die Verteilungen
verzerrt.
independent fit to the
combined
leptonic and
hadronic data (without
assuming
universality)
described in Section 11.2. The lower plots show the residuals to the fit. For the electrons, the dashed
curves show the contributions of the pure s-channel, and t-channel plus s − t interference, respectively.
110
9.4 Die Z 0 und W ± Bosonen
211
kurven bestimmt:
MZ = 91.1882 ± 0.0022 GeV,
Γ = 2.4952 ± 0.0023 GeV
Die Zerfälle in geladene Leptonen und Hadronen sind direkt messbar. Innerhalb der experimentellen Unsicherheit von 0.3% sind die leptonischen Breiten wie erwartet gleich
Γee = Γµµ = Γτ τ = 84.057 ± 0.099 MeV
Die hadronische Breite ist Γhad = 1743.8 ± 2.2 MeV.
9.4.5
Anzahl der Neutrinos
Die Zerfälle des Z 0 in Neutrinos sind natürlich “unsichtbar”. Wie kann man Information darüber
gewinnen? Die Idee ist, auszunutzen, dass die totale Breite gleich der Summe der partiellen
Breiten ist
Γ = Γee + Γµµ + Γτ τ + Nν · Γνν + Γhad
(9.29)
mit Γhad = Γ(Z 0 → Hadronen). Hier nimmt man an, dass die Zerfallsbreiten der drei Neutrinokanäle identisch sind, wie vom Standard-Modell vorhergesagt. Die Anzahl Nν der verschiedenen
Neutrinosorten ist ein freier Parameter.
Daher beträgt die Breite für unsichtbare Zerfälle
Γunsichtbar = Γ − (Γee + Γµµ + Γτ τ ) − Γhad = 499.4 ± 1.7 MeV
Theoretisch trägt jede Neutrino-Sorte mit 167.1±0.3 MeV zur Breite Γunsichtbar bei. Daher kann
man die Zahl der verschiedenen Neutrinos berechnen
Nν = 2.994 ± 0.012.
Dies ist sicherlich eines der wichtigsten LEP-Resultate. Es bedeutet, dass es genau die drei
bekannten Leptonfamilien (νe , e− ), (νµ , µ− ), (ντ , τ − ) gibt, und aus Symmetriegründen wahrscheinlich auch genau die drei bekannten Quarkfamilien (u, d’), (c, s’), (t, b’). Bei der Grenze an
der Zahl der Neutrinos muß man beachten, daß sie nur für Neutrinos gilt, die so kleine Massen
haben, daß sie im Zerfall des Z 0 entstehen können. In Abb. 9.19 ist die Breit-Wigner Resonanz
gezeigt mit Meßdaten und Rechnungen für 2, 3 und 4 Neutrinos. Wie man sieht, stimmen die
Daten hervorragend überein mit Nν = 3.
212
Schwache Wechselwirkungen
40
35
2 ν's
3 ν's
4 ν's
30
ALEPH
DELPHI
L3
OPAL
σ (nb)
25
20
15
10
5
0
87
88
89
90
91
92
93
√ s = Ecm (GeV)
94
95
96
Abbildung 9.19: Massenverteilung des Z 0 mit Rechnungen für 2, 3 und 4 Neutrinosorten. Die
Daten stammen von allen vier Experimenten vom Speicherring LEP.
9.5 Mischung von 3 Familien: CP Verletzung und Top Quark
9.5
Mischung von 3 Familien: CP Verletzung und Top
Quark
Das Konzept der Quarkmischung wird erfolgreich ausgedehnt auf 3 Familien. Das geladene W
vermittelt Übergänge in drei Dubletts:
u
d0
c
s0
t
b0
Ladung
+ 32
− 13
Also:
W − → ud0
W − → cs0
W − → tb0
Eine unitäre 3 × 3 Matrix verbindet die gemischten Zustände der schwachen Wechselwirkung
d0 , s0 , b0 mit den Zuständen d, s, b.
 
  
Vud Vus Vub
d
d0
 s0  =  Vcd Vcs Vcb  ·  s 
b0
Vtd Vts Vtb
b

Sie wird Cabibbo-Kobayashi-Maskawa Matrix genannt. Diese Matrix wurde schon 1973 diskutiert vor dem Auffinden des Charmquarks! (Sie enthält die Cabibbo Matrix, die im vorigen
Abschnitt eingeführt wurde.) Die Interpretation der Matrixelemente ist wieder wie folgt:
Ein Übergang u → d0 wird durch einen Faktor Vud in der Amplitude beschrieben, |Vud |2 im
Wirkungsquerschnitt oder Zerfallsbreite.
gud = gW Vud
Entsprechend ein Übergang t → b:
gtb = gW Vtb
In der Näherung, daß es nur 4 Quarks gibt, die durch die Cabibbomatrix beschrieben werden,
wäre Vud = cosθc .
Die Matrixelemente müssen experimentell bestimmt werden. Es ist zunächst wichtig, festzustellen, wieviele freie Parameter solch eine Matrix mit 9 Elementen enthält. Das wollen wir nicht
im einzelnen tun. Es kommt heraus, daß 4 reelle Parameter die Matrix beschreiben. Man kann
sie deshalb nicht mehr als Drehung in 3 Dimensionen interpretieren, dafür braucht man nur
3 Parameter (z.B. 3 Eulerwinkel). Der 4. Parameter wird unten klarer, man führt an einigen
Stellen komplexe Zahlen ein und spricht von einer komplexen ‘Phase’.
Es gibt viele explizite Darstellungen dieser Matrix, wir werden unten eine kennenlernen. Es
ist eines der Ziele heutiger Messungen, die Matrixelemente so gut zu bestimmen, daß man
nachprüfen kann, ob die Matrix tatsächlich unitär ist.
Unitarität heißt für die CKM Matrix: Vik∗ Vij = δkj . Für k = 2 und j = 1 lautet diese Bedingung:
V12∗ V11 + V22∗ V21 + V32∗ V31 = 0
∗
Vus
Vud + Vcs∗ Vcd + Vts∗ Vtd = 0
213
214
Schwache Wechselwirkungen
Experimentelle Bestimmung der Matrixelemente Man bestimmt die Elemente oft aus
Zerfällen von Hadronen.
|Vud | = 0.9740 ± 0.0010 wird aus dem Vergleich von Kern β Zerfällen mit Myonzerfall bestimmt.
|Vus | = 0.2205 ± . . . wird aus Zerfällen von K Mesonen, z.B. K − → π 0 e− νe bestimmt.
Vub ist schwer zu bestimmen, da Übergänge von der 3. in die 1. Familie sehr selten sind. In Hamburg (ARGUS Experiment am DORIS e+ e− Speicherring) wurde erstmals gezeigt, daß dieser
Übergang überhaupt auftritt. Der heutige Bestwert stammt von Messungen von B Zerfällen
(B → π`ν` , CLEO Experiment, Cornell):
|Vub | = 0.003 ± 0.0008.
Die Bestwerte sind heute insgesamt:


 
0.975 0.223 0.004
Vud Vus Vub
VCKM =  Vcd Vcs Vcb  =  0.222 0.974 0.040 
0.009 0.039 0.999
Vtd Vts Vtb
Vergleicht man die Zahlenwerte der 9 Matrixelemente, soweit sie bekannt sind, so sieht man
eine hierarchische Ordnung: die Diagonalelemente sind sehr nahe bei 1, d.h. die Übergänge in
den ursprünglichen “ungemischten”Familien sind am wahrscheinlichsten. Man sieht, daß die
Übergänge von der 3. Familie in die 2. klein sind und in die 1. noch kleiner. Die 3. Familie ist
fast entkoppelt vom Rest.
Wählt man folgende Schreibweise, in der die Familien durchnummeriert sind:


V11 V12 V13
VCKM =  V21 V22 V23  ,
V31 V32 V33
so kann man schreiben:
|V12 | = |V21 | ∼ λ ∼ 0.22
|V23 | = |V32 | ∼ λ2 ∼ 0.05
|V13 | = |V31 | ∼ λ3 ∼ 0.01
wobei λ ≈ sinθc , d.h. λ ≈ 0.22. Das wird in einer bekannten Parametrisierung ausgenutzt, der
Wolfenstein Parametrisierung, die 4 reelle Parameter λ, ρ, η und A benutzt.


2
1 − λ2
λ
Aλ3 (ρ − iη)




2
λ
2

 + O(λ4 )
VCKM = 
−λ
1− 2
Aλ



Aλ3 (1 − ρ − iη) −Aη 2
1
Die CKM Matrix enthält in der Wolfensteindarstellung zwei komplexe Elemente, Vtd und Vub .
Es stellt sich heraus, daß η 6= 0 zu einer CP Verletzung führt.1
1
Das hängt damit zusammen, daß für eine Reaktion A → B, die durch ein Matrixelement beschrieben wird,
die ‘Rückreaktion’ B → A durch das konjugiert komplexe Matrixelement beschrieben wird.
9.5 Mischung von 3 Familien: CP Verletzung und Top Quark
Wir hatten im Kapitel über Symmetrien schon die CP Eigenzustände der neutralen Kaonen
0
kennengelernt. Wir hatten gesehen, daß K 0 in K übergehen kann. CP Verletzung wurde
beobachtet, als man sah, daß der CP = −1 Eigenzustand K20 nicht nur in 3 Pionen zerfällt, die
ebenfalls CP = −1 haben sondern zu einem geringen Anteil auch in 2 Pionen. Eine Erklärung
der CP Verletzung im Standard Modell ist hier nun möglicherweise durch die CKM Matrix
gefunden.
Kobayashi hat bereits 1973 erkannt, daß es CP Verletzung über dieser Quarkmischung nur
geben kann, wenn man mindestens 3 Familien hat. In einer 2 × 2 Matrix kann man immer
alle Parameter reell wählen (z.B. θc für die Cabibbo Matrix). Da bis heute das Verständnis
der CP Verletzung nur bruchstückhaft ist, ist es eines der ehrgeizigen Ziele der jetzt laufenden
Experimente, das Wissen darüber zu erweitern.
Es wurden eigens Speicherringe mit extrem hoher Luminosität gebaut, einer, PEP II, am SLAC
(California), an dem das Experiment BABAR mißt. Der andere ist KEKB mit dem Experiment
BELLE in Japan. Man produziert bei den B Fabriken mit hoher Rate das Υ(4s) Meson:
e+ e− → Υ(4s) → BB
Υ(4s) ist ein bb Zustand mit der Masse 10.58 GeV, der vorwiegend in B Mesonen zerfällt. Die
Messungen werden an den Zerfallsproducten der B Mesonen durchgeführt. Ein untersuchter
Zerfall ist
B 0 → J/ψ + Ks0 ,
B 0 → J/ψ + Ks0 .
Man versucht festzustellen, ob die Zerfallsrate von B 0 und B 0 in diesen Endzustand, der ein
CP Eigenzustand ist (Übungsaufgabe), gleich oder unterschiedlich ist.
0
Das B 0 kann, ähnlich wie das K 0 , oszillieren, d.h. es kann in ein B übergehen.
Das Mischungsdiagramm für B enthält das CKM-Matrixelement Vtd , welches komplex ist. Weiter ist das Matrixelement Vtb enthalten, welches nahezu 1 ist. Daher erwartet man, daß die
Oszillationswahrscheinlichkeit im B 0 System wesentlich größer ist als im K 0 System, welches
an der entsprechenden Stelle Vcs hat.
Die Messungen ergeben Werte für die Parameter ρ und η der Wolfenstein Parametrisierung,
diese sind in Abb. 9.21 dargestellt. Es ist besonders interessant, herauszufinden, ob η 6= 0 ist,
d.h. ob es wirklich komplexe Elemente gibt. Man sieht, daß alle Messungen zusammen auf η 6= 0
hindeuten, daß aber noch bessere Messungen wünschenswert wären.
9.5.1
Entdeckung des Top Quarks
Das sechste Quark wurde 1994/5 von CDF Experiment am Fermilab (USA) entdeckt. Es war
schon lange gesucht und erwartet worden. Erst die Entdeckung der Oszillationen von B 0 Mesonen und die Messung deren Stärke (vom ARGUS Experiment in Hamburg!) gab jedoch einen
Hinweis, daß seine Masse extrem schwer sein würde. Die Präzisionsexperimente auf dem Z 0 ,
die Anfang der 90’er Jahre durchgeführt wurden, konnten eine recht genaue Massenvorhersage
machen: indirekt führt das top Quark zu Korrekturen von gemessenen Wirkungsquerschnitten,
die empfindlich auf die Masse sind.
Der direkte Nachweis erfolgte folgendermaßen. In pp Wechselwirkungen am Fermilab (Schwerpunktsenergie 1.9 TeV) werden top Quarks dominant paarweise erzeugt.
pp → tt.
Der Wirkungsquerschnitt ist 7.5 pb, etwa 10 Größenordnungen unter dem totalen inelastischen
Wirkungsquerschnitt pp →Hadronen (s. Fig. 9.22). Die schweren Quarks zerfallen schwach, in
215
216
Schwache Wechselwirkungen
s
d
Vtd
K0
K
d
b
Vcs
t
Vtb
B0
s
u, c, t
Vtd
d
Vtd
W
B
W
d
t
Vtd
0
0
b
Vtb
0
0
Abbildung 9.20: Oszillationen im K 0 − K System und im B 0 − B System. Hier läuft die Zeit
von links nach rechts!
folgender Kette:
t → bW+
Das W ist hier reell, da die top Masse wesentlich größer als die W Masse ist. Das W zerfällt
leptonisch oder hadronisch:
W + → ` + ν`
W + → Hadronen, Jets
Ebenso das b Quark:
b → c`− ν `
b → c W − → Hadronen, Jets.
Man hat also folgende Signaturen:
pp → tt + X → b qq 0 + b qq 0 X
→ b `+ ν` + b qq 0 X
→ b ` + ν` + b ` − ν ` X
44%, 6 Jets
30%, 4 Jets + 1 Lepton, fehlende Energie
5%, 2 Jets + 2 Leptonen, fehlende Energie
Bei der Rekonstruktion von top Quarks spielt der Nachweis des b Quarks eine wesentliche
Rolle. Das b Quark hat eine relativ lange Lebensdauer, da das entsprechende Matrixelement
Vus relativ klein ist. Die Hadronen, die sich aus dem b Quark durch Hadronisation bilden, leben
so lange, daß man ihren Flugweg im Detektor nachweisen kann, s. auch Abb. 9.23. Dazu benutzt
man hochpräzise Mikrovertexdetektoren, die meist als Siliziumstreifendetektoren verwirklicht
werden (s. Kap. 5.2.5).
Die Selektion von top Ereignissen benutzt als Signatur:
9.5 Mischung von 3 Familien: CP Verletzung und Top Quark
1
∆md
217
∆ms/∆md
∆md
|εK|
η
sin 2βWA
0
|Vub/Vcb|
|εK|
-1
CKM
fitter
-1
0
1
2
ρ
Cross section (barns)
Abbildung 9.21: Darstellung verschiedener Messungen zur CP Verletzung in der ρ − η Ebene.
Die schrägen Bänder, die von ρ = 1, η = 0 ausgehen, repräsentieren die BABAR Messungen.
Der Bestwert aller anderen Experimente ist in dem Bereich um ρ ∼ 0.2, η ∼ 0.3 zu finden, was
gut mit den ersten Messungen von BABAR übereinstimmt.
1
Total inelastic
1 x 1010
-2
10
-4
bb
10
6 x 106
-6
10
W
-8
4000
400
10
Z
-10
10
tt
1
-12
10
-14
10
Higgs (ZH + WH)
-16
10
100
120
140
160
180
200
Higgs mass (GeV/c2)
Abbildung 9.22: Wirkungsquerschnitte für pp Annihilation (als Funktion der Higgsmasse).
218
Schwache Wechselwirkungen
tt Event
SVX Display
Run 40758 Event44414
CDF
DKA100:[DAGWOOD.DATA]W_52.PAD 24SEP92 5:02:46 28-FEB-95
PV
0.02
0.02
-16.31
Jet 3
Jet 2
Jet 1
l1
l2
e
Jet 4
+
MFit
top = 170
ν
10 GeV/c2
l1
= 4.5 mm
l2
= 2.2 mm
Pt MAX 5 G
Y 2.002 c
X 2.645 c
24 September, 1992
run #40758, event #44414
Abbildung 9.23: tt Ereignis registriert vom CDF Experiment am pp Speicherring Tevatron.
1. ein Lepton mit hohem Transversalimpuls
2. fehlenden Transversalimpuls, der auf das Neutrino zurückzuführen ist.
3. einen Jet, der einen Ursprungspunkt (‘Vertex’) hat, der deutlich von dem des Kollisionspunktes von pp unterschieden ist.
Nach Punkt 1) und 2) hat man noch sehr viele W Ereignisse. Mithilfe von Kriterium 3) kann
man diese reduzieren. Man berechnet die invariante Masse aus den Jets, den Leptonen und dem
fehlenden Viererimpuls. Diese ist in Abb. 9.24 zusammen mit verschiedenen Simulationsrechnungen dargestellt.
In Abb. 9.26 sind alle aktuellen Messungen von den CDF– und D0–Experimenten am Fermilab
zusammengefaßt. Der heutige Bestwert aus allen Tevatron Messungen ist:
mt = 174.3 ± 5.1 GeV.
Indirekte Vorhersagen durch andere Experimente, hauptsächlich durch LEP Messungen, mithilfe des Standard Modells ergeben: mt = 168.2+9.6
−7.4 GeV.
Die Quarkmassen sind in Abb. 9.27 aufgetragen. Sie reichen von wenigen eV bis zu ∼ 175 GeV.
Die relativen Fehler an den Quarkmassen sind kleiner bei den schweren Quarks. Es sei hier
wiederholt, daß die Quarkmassen völlig unverstanden sind.
2
Events/(10 GeV/c )
9.5 Mischung von 3 Familien: CP Verletzung und Top Quark
15
10
5
0
100
125
150
175
200
225
250
275
2
Reconstructed Mass (GeV/c )
Abbildung 9.24: Rekonstruierte Top Quark Masse für Ereignisse von CDF; das durchgezogene
Histogramm stellt die Daten nach Selektionskriterium 1) und 2) dar, das strich-punktierte den
simulierten Untergrund von W Zerfällen und das dunkel schattierte stellt dia Daten dar, wenn
man auch eine b Quark Signatur (Vertex tag) verlangt (Kriterium 3)).
∆ln(likelihood)
6
1
0
-1
160
170
180
190
2
Top Mass (GeV/c )
4
2
Events/(10 GeV/c )
5
2
3
2
1
0
80
100
120
140
160
180
200
220
240
260
280
2
Reconstructed Mass (GeV/c )
Abbildung 9.25: Rekonstruierte Top Quark Masse für Ereignisse von CDF; das durchgezogene
Histogramm stellt die Daten nach Kriterium 1) – 3) dar, das gestrichelte den simulierten Zerfall
des top Quarks und das gepunktete Histogramm stellt den Untergrund dar.
219
220
Schwache Wechselwirkungen
Abbildung 9.26: Messungen der top Quarkmasse mit verschiedenen Methoden vom CDF und
D0 Experiment.
10 2
10
1
10
10
10
10
-1
-2
-3
-4
Abbildung 9.27: Massen der Quarks und geladenen Leptonen. Die Breite der Bänder gibt die
Unsicherheit an.
Kapitel 10
Neutrinophysik
Bisher haben wir folgende Eigenschaften der Neutrinos teils stillschweigend angenommen, teils
aus Experimenten geschlossen:
Masse
el. Ladung
Spin
Leptonzahl
(Leptonladung)
Helizität
mν
Qν
Sν
Lν
Lν
λν
λν
=
=
=
=
=
=
=
0
0
1
2
1 Lνe 6= Lνµ 6= Lντ
−1
−1
+1
Neutrinos haben nur schwache Wechselwirkung, d.h. die Wirkungsquerschnitte sind sehr klein.
In den letzten Jahren wurden folgende Fragen untersucht, die miteinander zusammenhängen:
• Ist mν wirklich 0? Die Obergrenzen aus Messungen am 3 H β Zerfall ergeben:
2
mν e <
∼ 3eV /c
• Ist die Leptonenzahl wirklich separat für νe , νµ und ντ erhalten?
• Ist das ν verschieden von ν?
• Wie groß ist die Lebensdauer des Neutrinos?
10.1
Neutrino Entdeckung und Nachweis
Das kontinuierliche Energie Spektrum der Elektronen bei β Zerfällen hat W. Pauli 1930 dazu
veranlaßt, ein neutrales (unsichtbares) Teilchen ν zu postulieren. Ein β Zerfall würde demnach
als Dreikörperzerfall vor sich gehen:
(Z, A) → (Z + 1, A) + e− + ν
Ein Zweikörperzerfall (Z, A) → (Z + 1, A) + e− würde ein monoenergetisches Elektron zur Folge
haben, was aber im Widerspruch zu sorgfältigen Messungen stand.
Pauli postulierte also einen Dreikörperzerfall. Das neutrale Teilchen sollte ein Fermion sein,
dann könnte man außer Energie und Impuls auch den Drehimpuls erhalten.
222
Neutrinophysik
Abbildung 10.1: Das Experiment von Reines, Cowan und Mitarbeitern zum Nachweis des Neutrinos.
Pauli nannte das neutrale Teilchen “Neutron”. Fermi führte nach Entdeckung des neutralen
Nukleons 1932, das man Neutron nannte, den Namen “Neutrino” für Paulis postuliertes Teilchen
ein.
Trotz vieler Bemühungen, das Neutrino nachzuweisen, gelang das erst 1959. In einer Serie von
historischen Versuchen, die Reines und Cowan am Savannah River Reaktor durchführten, gelang
schließlich der Nachweis. An einem Reaktor steht ein hoher Fluß von Neutrinos zur Verfügung.
In heutiger Notation ist jeder β Zerfall durch folgende Nukleonumwandlung zu erklären:
1) n → p + e− + ν e
Aus dem Reaktor kommen also Antineutrinos. Im Prinzip sollte dann auch folgende Reaktion
möglich sein:
2) ν e + p → n + e+ (Erhaltung der e-Lepton-Zahl). Diese Reaktion nennt man “inverser
β-Zerfall”.
Der Nachweis der Reaktion gelang Reines und Cowan. Sie haben sowohl das e+ in folgender
Reaktion nachgewiesen:
3) e+ + e− → γ + γ
als auch das Neutron über:
4) n +
A
48 Cd
→
A+1
48 Cd
+γ
Das Neutron aus 2) muß zunächst durch Stöße abgebremst werden, das dauert einige µs. Es
wurde im Experiment folgende charakteristische Signatur nachgewiesen. Das Signal der beiden
Photonen muß einige µs (vor) dem Signal des Neutrons erfolgen. Die Energien der 2 prompten
Photonen müssen je 0.511 MeV betragen. Das Experimentprinzip ist in Abb. 10.1 skizziert.
10.2 Bestimmung der Neutrinomasse
10.2
223
Bestimmung der Neutrinomasse
Im PDG 2002 sind folgende Grenzen zu finden:
2
mν e <
∼ 3 eV/c
mνµ < 0.17 MeV/c2
mν τ
< 18.2 MeV/c2
Die beste Grenze gilt also für das νe . Sie stammt aus Messungen am Tritium Zerfall:
3
H→
3
He + e− + ν e
Der Massenunterschied ist m (3 H) - m (3 He) = 0.5296 MeV/c2 . Da die Masse des Elektrons
me = 0.510999 MeV/c2 ist, bleibt nur wenig Energie für das Neutrino übrig und eine endliche Masse sollte einen Einfluß auf das gemessene Energiespektrum der Elektronen haben. Man
vermißt das Energiespektrum des Elektrons und analysiert es genau in der Nähe der höchsten
Energie (“Endpunkt”). Es wird eine Auftragungsart gewählt, die näherungsweise zu einer Geraden führt, falls die Neutrinomasse mν = 0 ist (Kurieplot, s. Abb. 10.2a). Abweichungen von
der Geraden können verursacht werden durch eine endliche Neutrinomasse, aber auch durch
Detektorauflösung. Die letztere muß also extrem gut verstanden werden.
Die zur Zeit präzisesten Experimente werden in Mainz und Troitsk (Russland) durchgeführt.
Alle derartigen Experimente haben in den letzten Jahren große Probleme gehabt wegen unverstandener Strukturen im Elektronenspektrum, die ad hoc korrigiert werden muessen. Das wird
sichtbar in Abb. 10.3, wo die besten Messungen für das Quadrat der Neutrinomasse gezeigt
sind. Die Werte sind alle negativ. Der heutige beste Wert ist m2ν = −(2.5 ± 3.3)eV2 . Er ist noch
nicht in der Abbildung enthalten, er ist mit 0 kompatibel.
(−)
Die Masse des νµ wird am besten durch den π Zerfall bestimmt: π ± → µ± + νµ . Das Pion wird
gestoppt und das Myonspektrum wird mit einem Magnetspektrometer gemessen. Die Massen
der beteiligten Teilchen sind genau bekannt.
Die Masse des ντ wird durch τ Zerfall bestimmt. Die τ Leptonen sind kurzlebig und sie werden
in e+ e− Annihilation erzeugt. Grenzen sind am LEP (e+ e− → Z 0 → τ + τ − ) bestimmt worden
und auf dem Y (4S), e+ e− → Y (4S) → τ + τ − + X.
Beim ντ benutzt man τ Zerfälle mit möglichst vielen geladenen Spuren:
z.B.
oder
τ − → 3h− + 2h+ + ντ
5 geladene Teilchen
(h = Hadronen)
τ − → π + π + π − π − π − ντ
τ − → 4h− + 3h+ + ντ
7 geladene Teilchen
Durch diese Auswahl bekommt man Zerfälle, bei denen die Energie der ντ gering ist.
Man bildet wieder Differenzen:
mν ≤ mτ − mHad
mν ≤ Ex = Eτ − EHad
√
s
wobei Eτ =
2
224
Neutrinophysik
Abbildung 10.2: a) Schematischer Kurieplot. b) β Spektrum des Tritiums als Funktion der kin.
Energie.
10.3 Neutrino mass and oscillations
Abbildung 10.3: Ältere Meßresultate für m2ν , der neueste Wert ist m2ν = −(2.5 ± 3.3)eV2
(PDG2002) und damit mit 0 kompatibel.
mHad ist die invariante Masse der Hadronen und EHad ihre Energie. Man trägt beide Größen
2
gegeneinander auf und leitet eine Massengrenze ab. Die Grenze ist mντ <
∼ 18.2 MeV/c .
Eine weitere Möglichkeit, die Neutrinomasse zu bestimmen und auch Information über die
Lebensdauer, Ladung und magnetisches Moment der Neutrinos zu bekommen, stellen im Prinzip
Neutrinos von entfernten Sternen dar. Supernova Ausbrüche führen zu einem Neutrinofluß. Da
diese sehr weit von uns entfernt sind, könnte man im Prinzip feststellen, ob die Neutrinos
weniger als Lichtgeschwindigkeit besitzen. Man muß dabei Annahmen über die Energie und
den Entstehungszeitpunkt machen.
10.3
Neutrino mass and oscillations
In the Standard Model the neutrino is a massless strictly neutral stable particle. From this
section onwards we will investigate the consequences of potential deviations from this assumption, in particular the case that neutrinos have a nonzero mass, which leads to the possibility
of neutrino oscillations.
10.3.1
Dirac and Majorana mass
Neutrinos are the only known fundamental fermions which do not carry electric charge. Already in 1937, Majorana established that such particles could have mass terms which couple the
“fermion” and “antifermion” fields in such a way that the resulting states are effectively their
own antiparticles. What we call antineutrino would then simply be the righthanded partner
of the lefthanded neutrino. Neutrinos exhibiting this behaviour are called Majorana neutrinos.
Such Majorana neutrinos violate the conservation of leptonic charge (Leptonnumber), as sug-
225
226
Neutrinophysik
Abbildung 10.4: Oszillationswahrscheinlichkeit, oben P (νe → νe ) für sin2 (2α) = 0.4. Unten:
2
P (νe → νµ ) als Funktion von ∆ = δm2 E·L .
gested by many extensions of the Standard Model. In this context the absence of experimental
evidence for leptonnumber violation is attributed to the smallness of the neutrino mass.
In the Standard Model all particles are basically massless. But there is a well defined prescription how particles - gauge bosons and fermions - acquire mass. This is the Higgs mechanism. Of
course, neutrinos could also acquire mass through the same mechanism as all other fermions, in
particular their charged lepton counterparts. Such neutrinos, called Dirac neutrinos, exhibit the
“usual” distinction between particles and antiparticles. Since the helicity of a particle with nonzero mass depends on the observer’s reference system, both left- and righthanded neutrinos and
antineutrinos must exist in this case. However, righthanded neutrinos and lefthanded antineutrinos would not participate in weak interactions, and hence appear “sterile”. The existence of
such sterile neutrinos is a direct prediction of any Standard Model extension with nonvanishing
Dirac neutrino mass terms. The only way to observe them would be through their gravitational
effects, or through neutrino oscillations, decay, or nonstandard interactions as discussed below.
Both kinds of mass terms can also occur simultaneously.
If the neutrinos have mass, the states of well defined mass must not necessarily be the same
states that have well defined leptonnumber. If one assumes that leptonnumber is not 100%
conserved oscillations are possible.
10.3.2
Neutrino oscillations (Zeitentwicklung)
In general, if neutrinos have mass and form mixed states, neutrino oscillations can occur. For
practical purposes it is often useful to consider the simplified case of only two neutrino flavours
taking part in the oscillations. Man muß zwischen “Flavoureigenzuständen” mit definierter
Leptonzahl und Masseneigenzuständen mit definierter Masse unterscheiden. Wir werden den
Fall νe und νµ betrachten.
νe
cos α sin α
ν1
=
.
(10.1)
νµ
− sin α cos α
ν2
Durch schwache Wechselwirkung werden z.B. in der Reaktion pp → d e+ νe Flavoureigenzustände νe erzeugt.
νe = ν1 · cos α + ν2 · sin α
Die Entwicklung in der Zeit ist bestimmt durch die Masseneigenzustände:
10.3 Neutrino mass and oscillations
227
Abbildung 10.5: Oszillationswahrscheinlichkeit P (νe → νe ) diesmal für den Mischungswinkel
sin2 (2α) = 0.83. Oben sind die drei unterschiedlichen Bereiche für L/E markiert.
ν1 (t) = ν1 (0) · e−iE1 t
ν2 (t) = ν2 (0) · e−iE2 t
mit
q
m2
p2 + m21 ≈ p + 1
2p
q
m2
E2 = p2 + m22 ≈ p + 2
2p
E1 =
wobei p = p1 = p2 (Impulserhaltung) und mi die Masse der Neutrinos νi ist.
Wir wählen als Anfangsbedingung zum Zeitpunkt t = 0:
νe (0) = 1
νµ (0) = 0
dann
und
ν2 (0) = νe (0) · sin α
ν1 (0) = νe (0) · cos α
(10.2)
(10.3)
Die rechten Beziehungen folgen durch Umkehrung von 10.1. Die Zeitabhängigkeit der Amplituden ist:
νe (t) = cos α · ν1 (t) + sin α · ν2 (t)
= cos α · ν1 (0) · e−iE1 t + sin α · ν2 (0) · e−iE2 t
Für ν1 (0) und ν2 (0) werden 10.2 und 10.3 eingesetzt:
νe (t) = νe (0) · cos2 α · e−iE1 t + sin2 α · e−iE2 t
228
Neutrinophysik
Dann ist die Wahrscheinlichkeit, nach der Zeit t immer noch ein νe zu finden:
|νe (t)|2
4
4
2
2
i(E2 −E1 )t
−i(E2 −E1 )t
=
cos
α
+
sin
α
+
sin
α
cos
α
·
e
+
e
P (νe → νe ) =
|νe (0)|2
(E2 − E1 ) · t
2
2
P (νe → νe ) = 1 − sin (2α) · sin
2
Die Wahrscheinlichkeit, nach Zeit t ein νµ zu finden, ist:
P (νe → νµ ) = 1 − P (νe → νe )
(E2 − E1 )t
2
2
P (νe → νµ ) = sin (2α) · sin
2
Beide Wahrscheinlichkeiten sind 0, falls α = 0 oder falls E2 = E1 (d.h. gleiche Massen)
m2
m2
Definiere δm2 = m22 − m21 . Dann ist mit Ei = p + i ≈ Ei + i und E = Ei .
2p
2Ei
2
P (νe → νe ) = 1 − sin (2α) · sin
2
1.27 · δm2 · L
E
wobei folgende Einheiten einzusetzen sind:
[δm2 ]
[L]
[E]
= (eV)2
= m
= MeV
Massendifferenz
Abstand von der Quelle
ν Energie
Die Oszillationswahrscheinlichkeit P ist in Abb. 10.4 und 10.5 für jeweils einen festen Mischungswinkel aufgetragen. In Abb. 10.5 sind die für die Praxis wichtigen Bereiche von L/E
markiert.
• If L/E 1/δm2 (E large or L small), the sin function can be approximated by a linear
function, and the “oscillation” effect is small even if the mixing angle is large.
• If L/E ∼ 1/δm2 , the actual sinusoidal oscillation pattern is accessible to observation.
• If L/E 1/δm2 (E small or L large), the sinusoidal oscillations become so fast that
they will be unmeasurable. In this case, only an average oscillation effect, proportional to
sin2 2α, can be observed.
10.4
Experimente zu Neutrino Oszillationen
Viele Experimente haben seit mehr als 30 Jahren nach Neutrino Oszillationen gesucht.
Es wurden Neutrinos aus folgenden Quellen benutzt, um nach Oszillationen zu suchen:
• Sonne
• Reaktoren
10.5 Neutrinos von der Sonne
229
• Beschleuniger
• Kosmische Strahlung → Atmosphärische Neutrinos
Man unterscheidet 2 Typen von Experimenten:
1) “Appearance” - Experimente
Suche nach νβ in Experimenten mit να Quellen; να → νβ .
Z.B., der Übergang νµ → ντ wird im Experiment OPERA gesucht werden durch Nachweis
des ντ über
ντ + N → τ − + X
2) “Disappearance” - Experimente
Man hat eine Neutrinoquelle, die einen Fluß να (L1 ) liefert. Man mißt die Rate να (L2 ) in
einiger Entfernung von der Quelle. Falls die Rate να (L2 ) kleiner ist als να (L1 ), so schließt
man auf einen Übergang von να in eine anderen Neutrinosorte.
Alle bisherigen Experimente, die ein Signal sehen, was sich als Oszillation interpretieren läßt,
sind vom Typ “Disappearance”. Einzige Ausnahme ist LSND.
10.5
Neutrinos von der Sonne
Die Entfernung von der Sonne ist sehr groß, L ≈ 1011 m. Der Fluß der Neutrinos kann genau
berechnet werden. Es gibt ein “Standardsonnenmodell” (SSM), das genaue Vorhersagen macht.
Die meisten Neutrinos in der Sonne werden in der sogenannten pp-Kette erzeugt (Abb. 10.6).
Sie haben Energien unterhalb von etwa 10 MeV. 99.75% sind sogar unterhalb von 0.42 MeV.
Das berechnete Spektrum ist in Abb. 10.7 zu sehen.
Man sieht aus der Abb. 10.6, daß alle Neutrinos, die von der Sonne kommen, vom Typ νe sind.
Der Fluß ist gut bekannt als Funktion der Energie (falls das SSM richtig ist).
Nachweis
Sonnenneutrinos sind wegen ihrer kleinen Energie nur sehr schwer nachzuweisen. Man benutzt
im wesentlichen 2 Methoden, die immer Detektoren mit großer Masse erfordern.
1) Radiochemisch Ein Beispiel ist das Experiment in der Homestake Mine in Minnesota
(USA) (R. Davis und Mitarbeiter), welches als erstes bemerkte, daß der nachgewiesene Neutrinofluß von der Sonne nur ein Bruchteil des berechneten war. Der Detektor nutzte die Reaktion:
νe +
37
Cl →
37
Ar + e−
Die Energieschwelle ist Eν > 814 keV, d.h. es werden nur die 7 Be und 8 B Neutrinos nachgewiesen.
Der Detektor bestand aus Tanks von Perchlorethylen (133 t Reinigungsflüssigkeit). Ein Meßlauf
dauert ca. 60 Tage. Dann werden die entstehenden 37 Ar Atome aus der Flüssigkeit ausgespült
und durch ihren radioaktiven Zerfall nachgewiesen. 37 Ar hat eine Halbwertzeit von 35 Tagen.
Ergebnis des Homestake Experimentes:
νe (gemessen)
= 0.33 ± 0.05
νe (berechnet)
230
Neutrinophysik
Abbildung 10.6: Die pp-Kette, die den grössten Bruchteil der Sonnenenergie liefert.
Abbildung 10.7: Das berechnete Sonnenspektrum als Funktion der Neutrino Energie in MeV.
10.5 Neutrinos von der Sonne
Abbildung 10.8: Oben: ältere Experimente zu Messung des solaren Neutroflusses. Es = Schwellenenergie. Mitte: Messungen von Davis et al. im Homestake Experiment zwischen 1970 und
1995. Die gestrichelte Linie gibt den Mittelwert an. Unten: Messungen im GALLEX Experiment
zwischen 1990 und 1995.
231
232
Neutrinophysik
Abbildung 10.9: Messungen des solaren Neutrinoflusses im Vergleich mit Rechnungen. Die Rechnungen sind jeweils für einen Experimenttyp dargestellt und daneben sind zum Vergleich die
Messungen. Man sieht das Defizit bei SAGE, GALLEX/GNO, Homestake, Kamiokande und
Superkamiokande. Bei den Messungen am Deuterium (SNO) zeigt nur die CC Messung ein
Defizit, während NC mit der rechnung übereinstimmt.
Andere radiochemische Experimente benutzen Gallium, welches den Vorteil einer niedrigeren
Energieschwelle hat. Man ist damit auch auf einen Teil der pp Neutrinos sensitiv. Die Ergebnisse
(Abb. 10.8 unten) bestätigen das gemessene Defizit, s. Abb. 10.9.
2) Čerenkov Experimente Der zweite Experimenttyp läuft in “Echtzeit”. In großen Wassertanks werden die Elektronen aus den Neutrinoreaktionen durch Čerenkoveffekt nachgewiesen.
Eine Zusammenfassung der Beobachtungen ist in Abb. 10.9 zu sehen.
Alle Experimente beobachten also ein Defizit gegenüber den Erwartungen.
Außer Oszillationen können natürlich auch Fehler im Sonnenmodell Ursache des Defizits sein.
Durch immer bessere Sonnenbeobachtung (Helioseismographie) wurden diese jedoch immer
unwahrscheinlicher.
Oszillationen könnten eine weitere Erklärung sein. Das Problem bei dem Typ “Disappearance”
Experiment ist, daß man nicht messen kann, in welchen Typ Neutrino sich die νe aus der Sonne
verwandeln.
Eine weitere Komplikation machte eine quantitative Interpretation lange schwierig. Die Sonnenneutrinos entstehen im Inneren der Sonne und durchqueren enorm viel Materie, bevor sie
ins Vakuum kommen und zu uns fliegen. In Materie ist der Oszillationsmechanismus aber komplizierter als oben beschrieben.
10.5 Neutrinos von der Sonne
233
Der dritte Experimenttyp, der hier erwähnt werden soll, hat erste Ergebnisse im Jahr 2001
vorgestellt. Es ist auch ein Experiment, das die Sonnenneutrinos mißt.
10.5.1
Sudbury Neutrino Observatory (SNO)
Es handelt sich wieder um ein Echtzeit Čerenkov Experiment, Abb. 10.10. Jedoch ist die
Flüssigkeit im Detektortank hier schweres Wasser, also D2 O.
Hier sind folgende Reaktionen mit Sonnenneutrinos möglich:
νe + d → pp e−
νx + d → pn νx
CC
NC
Die erste Reaktion geht über W ± -Austausch (CC = Changed Current), während die letzte
über Z 0 Austausch (NC = Neutral Current) verläuft. In der NC Reaktion ist der Wirkungsquerschnitt für alle Neutrinosorten ungefähr gleich.
Ergebnis: In der CC Reaktion wird bei SNO ein ähnliches Defizit gefunden wie in den anderen
Experimenten mit Sonnenneutrinos.
In der NC Reaktion sieht SNO genau den im SSM berechneten Fluß! Das legt den Schluß nahe,
daß tatsächlich νe wegoszillieren auf dem Weg von der Sonne hierher.
Man hat außerdem eine Bestätigung, daß das Sonnenmodell stimmt.
Bei SNO kann noch eine weitere Reaktion gemessen werden: elastische Streuung an Elektronen:
νx + e − → ν x + e −
ES
Diese Reaktion wird dominant von νe gemacht (über geladenen Strom) aber es tragen auch
Neutrale Strom Reaktionen bei, dann können wieder alle Neutrinos teilnehmen. Der Fluss der
Neutrinos wird mit allen 3 Reaktionen gemessen. Daraus kann man dann Abb. 10.11 rekonstruieren.
Abbildung 10.10: Der SNO Detektor, der in Kanada betrieben wird.
234
Neutrinophysik
8
SNO
φES
φµτ (106 cm−2s−1)
7
SNO
φCC
6
5
4
φSSM
3
SNO
φNC
2
1
0
0
1
2
3
4
φe (106 cm−2s−1)
5
6
∆m2(eV2)
Abbildung 10.11: Der gemessene Neutrinofluss von νµ und ντ aufgetragen gegen den von
νe rekonstruiert aus den Messungen von SNO. CC=charged current, NC=neutral current,
ES=elastische Streuung, SSM=Standard Solar Model.
tan θ
2
Abbildung 10.12: ∆m2 − tan2 θ Ebene für Sonnenneutrinos. Es gibt mehrere Regionen, die mit
den Daten bis einschließlich SNO verträglich sind. Nimmt man auch die KAMLAND Messung
dazu, so bleibt nur eine Lösung übrig: ∆m2 ∼ 4 · 10−5 eV2 ; tan2 θ ∼ 0.5.
10.6 Atmosphärische Neutrinos
235
Abbildung 10.13: Der gemessene Neutrinofluss von ν e von verschiedenen Reaktoren als Funktion
der Entfernung. Man sieht das Defizit bei KAMLAND, welches eine Entfernung von 180 km
hat.
Ein Experiment, welches Reaktorneutrinos misßt, ist KAMLAND. Der Detektor ist ca. 180 km
von den Reaktoren entfernt. Der gemessene Fluss ist für einige Reaktorexperimente in Abb.
10.13 zu sehen.
Nach der KAMLAND Messung bleibt als wahrscheinlichste Lösung für Sonnenneutrinos übrig
(s. Abb. 10.12):
∆m2 ∼ 4 · 10−5 eV2 ; sin2 2α ∼ 0.9
10.6
Atmosphärische Neutrinos
Der Fluß von Neutrinos (νe ) von der Sonne, der geringer war als erwartet, überzeugte niemanden von der Möglichkeit, daß Oszillationen stattfinden. Es wurden aber weitere Experimente
gemacht. Das Superkamiokande Experiment (Nachfolgeexperiment des kleineren Kamiokande
Experiments), fand einen weiteren Defizit an Neutrinos. Diesmal handelt es sich jedoch um
Neutrinos, die in der Erdatmosphäre durch kosmische Strahlung entstehen.
Kosmische Strahlung besteht im wesentlichen aus Protonen. Diese können mit den Molekülen
der Erdatmosphäre in hadronischen Reaktionen u.a. geladene Pionen erzeugen. Diese zerfallen
gemäß:
(−)
µ
π ± → µ± + ν
Das Myon zerfällt weiter gemäß:
(−)
(−)
µ
µ± → e ± + ν e + ν
236
Neutrinophysik
Abbildung 10.14: Oben: Der Kamiokande Detektor; unten: Superkamiokande
10.6 Atmosphärische Neutrinos
237
Moderate Energy Sample
J. Goodman – LP01
Abbildung 10.15: Messungen der Winkelverteilung von Elektron Neutrinos (links) und Myon
Neutrinos rechts im Detektor Superkamiokande. cos θ = −1 heisst, dass die Teilchen von unten
kommen. Man sieht, dass links die Daten gut durch die Histogramme beschrieben werden.
Rechts dagegen liegt die Rate der Myonen bei cos θ < 0 unter dem dunklen Histogramm,
das die Erwartung ohne Oszillationen darstellt. Das helle Histogramm, welches Oszillationen
berücksichtigt, beschreibt die Daten dagegen gut.
238
Neutrinophysik
Man erwartet also in erster Näherung ein Verhältnis von Nνµ : Nνe ≈ 2 : 1. Diese Neutrinos
können wesentlich höhere Energien haben als die Sonnenneutrinos. Sie werden im Wassertank
durch Čerenkovstrahlung der geladenen Leptonen nachgewiesen, die bei den Reaktionen entstehen:
ν µ + p → µ+ + n
νµ + n → µ − + p
ν e + p → e+ + n
νe + n → e − + p
oder inelastisch
ν µ + N → µ+ + X
νµ + N → µ− + X
ν e + N → e+ + X
νe + N → e− + X
N bezeichnet ein Nukleon, X einen hadronischen Endzustand.
Myonen und Elektronen können im Detektor unterschieden werden. Die Messung ergibt die
Richtung und Sorte der Neutrinos und grobe Energieinformation. Nun kommen Neutrinos in den
Detektor, die in der Luft oberhalb erzeugt wurden und solche, die die gesamte Erde durchquert
haben und von unten kommen. Der Wegunterschied ist ∼ 12750 km. Man vergleicht die Zahl
von oben und von unten und findet bei Myonneutrinos ein Defizit für diejenigen von unten. Für
Elektronneutrinos ist das Verhältnis wie erwartet.
Das Defizit kann man mit der Hypothese, daß νµ → νx oszilliert, erklären, L/E ≈ 5 · 104 km .
GeV
Auswertung der Daten ergibt:
∆m2 ∼ 3 · 10−3 (eV )2
sin2 (2α) ∼ 1
Die Werte sind in Abb. 10.16 in der Ebene ∆m2 sin2 2α dargestellt, sie sind anders als bei
Sonnenneutrinos.
Falls die Oszillationshypothese richtig ist, gibt es also mindestens zwei ∆m2 Werte, z.B. zwischen
den ν1 und ν2 und dem ν2 und ν3 . Diese Hypothese ist in Abb. 10.17 zu sehen.
10.6 Atmosphärische Neutrinos
239
CHORUS
100
NOMAD
1000
∆m2 [eV2]
10
CD
HS
W
1
0.1
0.01
νµ↔ντ
Super-Kamiokande
atmospheric neutrino
0.001
10–4
10–3
0.01
0.1
1
sin22θ
Abbildung 10.16: ∆m2 − sin2 2θ Ebene für Oszillationen νµ ↔ ντ . Die Messung von Superkamiokande an atmosphärischen Neutrinos ist unten rechts zu sehen. Oben sind Grenzen von
Beschleunigerexperimenten gezeigt, wobei die ausgeschlossene Region rechts und oberhalb der
Kurven liegt.
(Mass) 2
2
∆m atm
} ∆m 2.
Abbildung 10.17: Schematische Darstellung von 3 Neutrinos νi mit definierter Masse und der
Zusammensetzung aus den Flavouranteilen. Rechts schraffiert: νµ , links schraffiert: ντ , kariert:
νe . Zum heutigen Zeitpunkt noch hypothetisch!