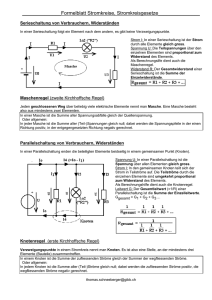
Stromrichtungen und Vorzeichen
Werbung

Kirchhoffsche Gesetze Es gibt zwei Kirchhoffsche Gesetze in elektrischen Netzwerken: 1. Maschenregel: die Summe der Spannungsgewinne entlang eines geschlossenen Weges ist gleich Null. Spannungsgewinne und Spannungsverluste heben einander auf. 2. Knotenregel: die Summe der in einen Teilbereich zufließenden Ströme ist gleich Null Zu- und abfließende Ströme heben einander auf. Insbesondere trifft diese Regel für jeden Knoten zu. Anwendung der Kirchhoffschen Gesetze zur Berechnung der Spannungen und Ströme in elektrischen Netzwerken Die Gesetze sind für Gleich- und Wechselstrom anwendbar. Man muss sich zuerst für eine Frequenz entscheiden, für die man die Stromflüsse und die Spannungen berechnen will. Die Superposition der Teillösungen für verschiedene Frequenzen ergibt die Gesamtlösung. Löst man die lineare inhomogene Differentialgleichung, dann beschreibt die homogene Lösung Einschwingvorgänge, und die partikuläre Lösung beschreibt den erzwungenen Schwingungszustand. Sehr einfach ist die Untersuchung des erzwungenen Schwingungszustandes. Amplitudenverhältnis von Spannung und Strom und deren Phasendifferenz werden als Polarkoordinaten des komlexen Widerstandes, der sogenannten Impedanz, verwendet. Die Netzwerkberechnung erfolgt bei Wechsel- und Gleichstrom nach denselben Methoden. Die Impedanzen werden für ϖ → 0 reell. Beispiel: In die Zweige einer gegebenen Schaltung G1 R1 I1 G2 R2 G3 R3 + G R U1 - trägt man Ströme ein. Dabei kann man so verfahren, dass man die Knotenregel durch die Art der Strombenennung erfüllt und dadurch überflüssige Variablen und Gleichungen einspart. Die hier dargestellte Maxwellsche Zykelmethode erfüllt die Knotenregel elegant. Dieselben Maschen, die für die geschlossenen Teilströme gewählt wurden, dienen der Aufstellung von Gleichungen zur Erfüllung der Maschengleichungen. Stromrichtungen und Vorzeichen Man wählt eine Richtung, in der man die Masche durchläuft und die Spannungen aufaddiert. Die Summe muss Null sein. Spannungsabfälle werden positiv gerechnet. Ein negatives Vorzeichen ist zu nehmen, wenn der angenommene Strom der gewählten Maschendurchlaufrichtung entgegen kommt. Spannungspfeile an Spannungsquellen sind deswegen von + nach – orientiert, dass der negativ zu rechnende Spannungsgewinn sich von selbst dadurch ergibt, dass man ein negatives Vorzeichen dann nimmt, wenn der Spannungspfeil der gewählten Maschendurchlaufrichtung entgegen kommt. Man rechnet so, als würde der Strom aus dem Pluspol einer Spannungsquelle treten, ungeachtet des Leitungsmechanismus durch Elektronen in Festkörpern. Aufstellung der Maschengleichungen − U 1 + R1 ⋅ I1 + R2 ⋅ ( I1 − I 2 ) = 0 U 2 − R2 ⋅ ( I1 − I 2 ) + R3 ⋅ ( I 2 − I 3 ) = 0 (1) − U 2 − R3 ⋅ ( I 2 − I 3 ) + R ⋅ I 3 = 0 Der Übersicht wegen werden die Gleichungen zuerst umgeordnet. Die Spannungsquelle U2 und die Stromquelle I1 sind vorgegeben. Gesucht sind U1, I2, I3. R2 1 0 R2 + R3 0 − R3 U 1 0 R1 + R2 U − R3 ⋅ I 2 = − 1 R2 ⋅ 2 I 0 1 R3 + R I 3 1 0 U 1 ∆ − R2 ( R3 + R) − R2 R3 0 R1 + R2 U −1 R3 + R R3 ⋅ − 1 R2 ⋅ 2 I2 = ∆ ⋅ 0 I I 0 R3 R2 + R3 1 0 1 3 ∆ := R2 R3 + R3 R + RR2 = R2 R3 R(G2 + G3 + G ) U 1 R2 R −1 I2 = ∆ ⋅ − R I R 3 2 So ist etwa I 3 = R1 R2 R3 R(G1 + G2 + G3 + G ) U 2 R2 ( R3 + R) ⋅ I1 R2 R3 G ⋅ (G3 ⋅ U 2 + I1 ) G2 + G3 + G (2) (3) Überlagerungsmethode nach Helmholtz In Gleichung (2) fällt auf, dass die beiden Spaltenvektoren der Matrix einer bestimmten Strom- oder Spannungsquelle zugeordnet sind. Die Lösung U 1 I 2 kann als Superposition von Teillösungen betrachtet werden, die durch I 3 U 2 0 0 und verursacht werden: I1 U 11 R2 R −1 I 21 = ∆ ⋅ − R I R 31 2 R1 R2 R3 R(G1 + G2 + G3 + G ) U 2 R2 ( R3 + R) ⋅ 0 R2 R3 U 12 R2 R −1 I 22 = ∆ ⋅ − R I R 32 2 R1 R2 R3 R(G1 + G2 + G3 + G ) 0 R2 ( R3 + R) ⋅ I1 R2 R3 U 1 U 11 U 12 I 2 = I 21 + I 22 I I I 3 31 32 U 2 U 2 0 = + I 1 0 I1 Für die Ausdrucksmittel der Schaltungsanalyse ist 1. ein verschwindender Strom mit der Auftrennung einer Leitungsverbindung identisch. 2. eine verschwindende Spannung mit einem Kurzschluss identisch. Die graphische Illustration der Teillösungen hat in neuen Schaltbildern zu erfolgen, in denen eine der gegebenen Spannungs- oder Stromquellen aufscheint. Die anderen Spannungsquellen werden durch Kurzschlüsse ersetzt, die anderen Stromquellen werden durch offene Verbindungen ersetzt. Die Gesamtlösung erhält man durch Addition aller Ströme und Spannungen in den entsprechenden Zweigen. Insbesondere dann, wenn nur einzelne Größen gesucht sind, zeigt sich die Eleganz der Methode in der Kombination mit Formeln für Parallel- und Serienschaltung, Stern- Dreieck- Umwandlung, Strom- und Spannungsteilerregel. Schließlich leiten sich diese rasch anzuwendenden Methoden von Gleichungssystemen her. Wir betrachten im Folgenden die Superposition in der Schaltungsdarstellung. Die drei Widerstände liegen an derselben Spannung, weshalb sich der Strom I1 direkt G proportional ( I = G ⋅ U ) zu den Leitwerten aufteilt. I 31 = ⋅ I1 G2 + G3 + G Der Gesamtleitwert ist am Strom I 22 1 = (G2 + G ) ⋅ G3 G . Der Strom I32 ist der Anteil G2 + G G2 + G3 + G 1 + R3 G2 + G (G + G ) ⋅ G3 G ⋅ G3 = 2 ⋅ U 2 , also I 32 = ⋅U 2 . G2 + G3 + G G2 + G3 + G Der gesuchte Strom I 3 = I 31 + I 32 = G ⋅ ( I1 + G3 ⋅ U 2 ) in Übereinstimmung mit G2 + G3 + G Gleichung (3). Das Strom- Spannungsverhalten des aktiven Zweipols Das Interesse galt dem konstanten passiven Bauteil R. Man kann stattdessen R durch eine Spannungsquelle oder durch eine Stromquelle ersetzen und den sich einstellenden Strom, bzw. die sich einstellende Spannung ausrechnen. Die Lösungsmenge muss in beiden Fällen dieselbe sein. 1. Externe Spannungsquelle vorgegeben Die Summe der vom Pluspol der Spannungsquelle U in die Schaltung fließenden Ströme ist I = − I1 − G3 ⋅ U 2 + (G2 + G3 ) ⋅ U die Summe der Spannungen ist U. 2. Externe Stromquelle vorgegeben (4a) Die Summe der Ströme ist I, die Summe der Spannungen ist U= I1 R ⋅U I + 2 2 + G2 + G3 R2 + R3 G2 + G3 (4b) Wie zu erwarten war, haben (4a) und (4b) dieselbe Lösungsmenge, denn R2 ⋅ R3 ⋅ (G2 + G3 ) = R2 + R3 . I + I1 + G3 ⋅ U 2 = (G2 + G3 ) ⋅ U (4c) Kehren wir wieder zum Anfang zurück! Dort war ein Widerstand gegeben, der ein festes Verhältnis von U und I bedeutet. Man substituiert U durch R.I und erhält wieder Glg. (3), jedoch mit negativem Vorzeichen vor I, weil zuletzt die Stromrichtung anders gewählt wurde. Zusammenfassung: es ist nicht nur allgemeiner, sondern auch übersichtlicher, mit Strom- und Spannungsquellen zu arbeiten als mit Widerständen.