So klein

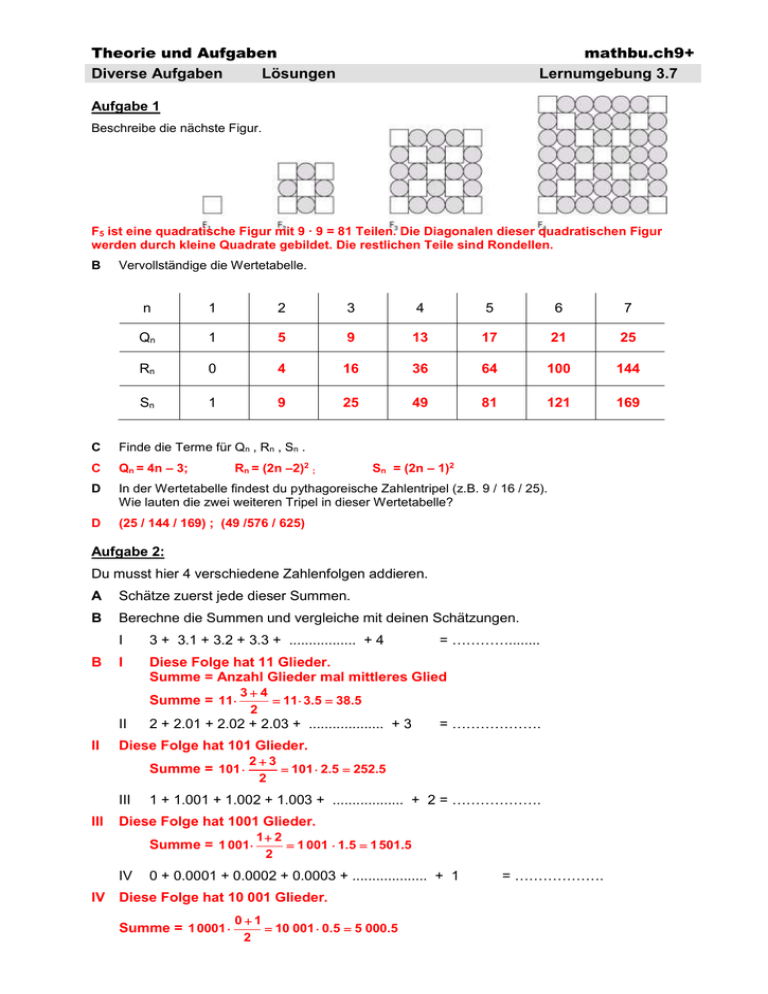
Theorie und Aufgaben
Diverse Aufgaben
Lösungen
mathbu.ch9+
Lernumgebung 3.7
Aufgabe 1
Beschreibe die nächste Figur.
F5 ist eine quadratische Figur mit 9 ∙ 9 = 81 Teilen. Die Diagonalen dieser quadratischen Figur
werden durch kleine Quadrate gebildet. Die restlichen Teile sind Rondellen.
B
Vervollständige die Wertetabelle.
n
1
2
3
4
5
6
7
Qn
1
5
9
13
17
21
25
Rn
0
4
16
36
64
100
144
Sn
1
9
25
49
81
121
169
C
Finde die Terme für Qn , Rn , Sn .
C
Qn = 4n – 3;
D
In der Wertetabelle findest du pythagoreische Zahlentripel (z.B. 9 / 16 / 25).
Wie lauten die zwei weiteren Tripel in dieser Wertetabelle?
D
(25 / 144 / 169) ; (49 /576 / 625)
Rn = (2n –2)2 ;
Sn = (2n – 1)2
Aufgabe 2:
Du musst hier 4 verschiedene Zahlenfolgen addieren.
A
Schätze zuerst jede dieser Summen.
B
Berechne die Summen und vergleiche mit deinen Schätzungen.
B
3 + 3.1 + 3.2 + 3.3 + ................. + 4
I
Diese Folge hat 11 Glieder.
Summe = Anzahl Glieder mal mittleres Glied
Summe = 11
II
II
34
 11 3.5  38.5
2
2 + 2.01 + 2.02 + 2.03 + ................... + 3
= ……………….
Diese Folge hat 101 Glieder.
Summe = 101 
III
III
= …………........
I
23
 101  2.5  252.5
2
1 + 1.001 + 1.002 + 1.003 + .................. + 2 = ……………….
Diese Folge hat 1001 Glieder.
Summe = 1 001
IV
1 2
 1 001  1.5  1 501.5
2
0 + 0.0001 + 0.0002 + 0.0003 + ................... + 1
IV Diese Folge hat 10 001 Glieder.
Summe = 1 0001 
01
 10 001  0.5  5 000.5
2
= ……………….
Theorie und Aufgaben
mathbu.ch9+
Aufgabe 3:
A
Beschreibe oder zeichne die nächste Figur.
A
Die nächste Figur F4 besteht aus 5 mal 5 mal 5
Würfel, bei denen die oberste rechte Reihe fehlt.
Es braucht somit 125 – 5 = 120 Würfel.
B Vervollständige die Wertetabelle.
n
1
2
3
4
5
6
Anzahl Würfel = wn
6
24
60
120
210
336
C
Gib einen Term für wn an, mit dem sich die Anzahl Würfel der n-ten Figur berechnen lässt.
C
wn = (n +1)3 – (n + 1) = n3 + 3n2 + 3n – n – 1 = n3 + 3n2 + 2n
D
Zeige, dass sich wn auch so darstellen lässt: wn = x  (x +1)  (x + 2)
D
Man zeigt: x(x +1)(x + 2) = x3 + 3x2 + 2x
oder man merkt in der Wertetabelle:
1  2  3 = 6 ; 2  3  4 = 24 ; 3  4  5 = 60 ; 4  5  6 = 120 ;
somit:
x  (x + 1)  (x + 2) = (x2 + x)  (x + 2) = x3 + 3x2 + 2x
5  6  7 = 210 ;
Aufgabe 4:
Setze die Zahlenfolgen fort und bestimme den Term Tx für die x-te Zahl.
Ix
1
2
3
4
5
6
7
Tx
1
4
9
16
25
36
49
Tx = x2
(Quadratzahlen)
IIx
1
2
3
4
5
6
7
Tx
1
3
6
10
15
21
28
Tx 
x
(x  1)
2
III
x
Tx
Tx = 2x – 1
(Dreieckszahlen)
1
2
3
4
5
6
7
1
3
5
7
9
11
13
(ungerade Zahlen)