schr. RP
Werbung
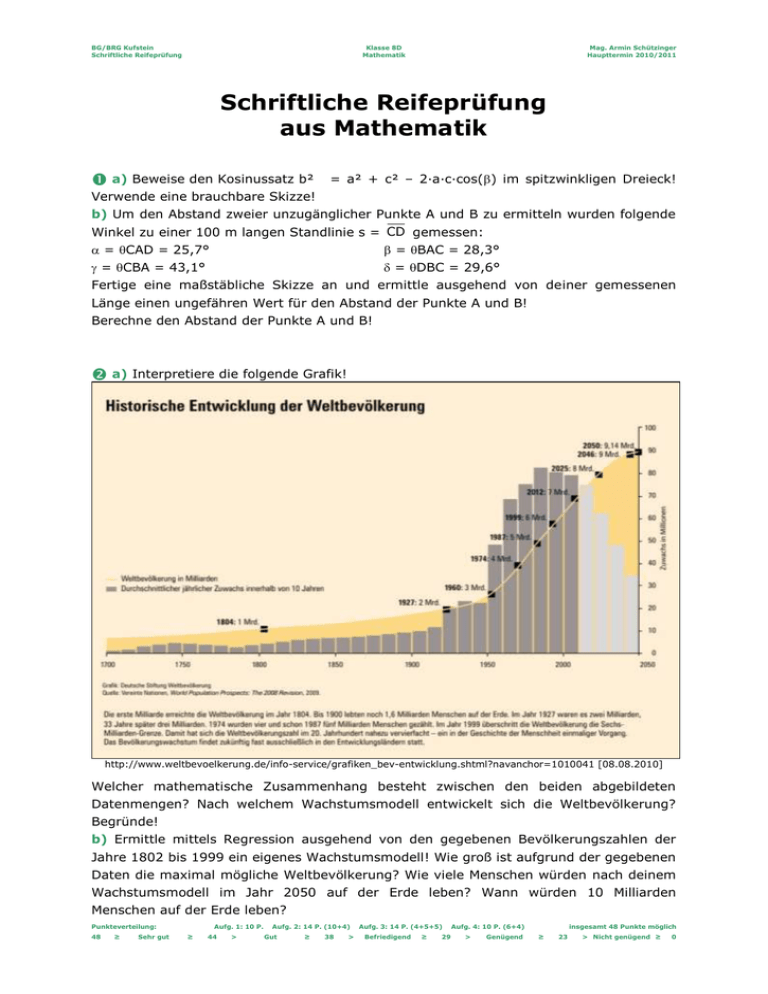
BG/BRG Kufstein Schriftliche Reifeprüfung Klasse 8D Mathematik Mag. Armin Schützinger Haupttermin 2010/2011 Schriftliche Reifeprüfung aus Mathematik a) Beweise den Kosinussatz b² = a² + c² – 2·a·c·cos() im spitzwinkligen Dreieck! Verwende eine brauchbare Skizze! b) Um den Abstand zweier unzugänglicher Punkte A und B zu ermitteln wurden folgende Winkel zu einer 100 m langen Standlinie s = CD gemessen: = CAD = 25,7° = BAC = 28,3° = CBA = 43,1° = DBC = 29,6° Fertige eine maßstäbliche Skizze an und ermittle ausgehend von deiner gemessenen Länge einen ungefähren Wert für den Abstand der Punkte A und B! Berechne den Abstand der Punkte A und B! a) Interpretiere die folgende Grafik! http://www.weltbevoelkerung.de/info-service/grafiken_bev-entwicklung.shtml?navanchor=1010041 [08.08.2010] Welcher mathematische Zusammenhang besteht zwischen den beiden abgebildeten Datenmengen? Nach welchem Wachstumsmodell entwickelt sich die Weltbevölkerung? Begründe! b) Ermittle mittels Regression ausgehend von den gegebenen Bevölkerungszahlen der Jahre 1802 bis 1999 ein eigenes Wachstumsmodell! Wie groß ist aufgrund der gegebenen Daten die maximal mögliche Weltbevölkerung? Wie viele Menschen würden nach deinem Wachstumsmodell im Jahr 2050 auf der Erde leben? Wann würden 10 Milliarden Menschen auf der Erde leben? Punkteverteilung: 48 ≥ Sehr gut Aufg. 1: 10 P. ≥ 44 > Aufg. 2: 14 P. (10+4) Gut ≥ 38 > Aufg. 3: 14 P. (4+5+5) Befriedigend ≥ 29 Aufg. 4: 10 P. (6+4) > Genügend insgesamt 48 Punkte möglich ≥ 23 > Nicht genügend ≥ 0 BG/BRG Kufstein Schriftliche Reifeprüfung Klasse 8D Mathematik Mag. Armin Schützinger Haupttermin 2010/2011 a) Aus fünf jeweils 20 cm breiten Brettern soll wie in der nebenstehenden Zeichnung eine Rinne gebaut werden. mittlere Brett liegt die beiden waagrecht, anschließenden sind unter Das Bretter demselben Winkel zur Waagrechten geneigt, die beiden äußeren Bretter sind unter demselben Winkel zur Waagrechten geneigt. Wie müssen die Winkel und gewählt werden, damit die Rinne möglichst große Querschnittfläche hat, und wie groß ist diese Fläche? b) Begründe mit den dir zur Verfügung stehenden Mitteln, warum die von dir gefundene Lösung maximale Querschnittfläche liefert! Ein Jahrmarktsbudenbesitzer veranstaltet folgendes Glücksspiel. Ein Spieler dreht drei Mal hintereinander an einem Glücksrad, bei dem ein 120° großer Sektor rot bemalt ist. Die Teilnahme am Spiel kostet 5 €. Bleibt das Glücksrad ein Mal im roten Bereich stehen, bekommt der Spieler 10 € ausbezahlt, er gewinnt also 5 €. Bleibt das Glücksrad zwei Mal im roten Sektor stehen, erhält er 20 € ausbezahlt, er hat also 15 € gewonnen. Erdreht er nie oder alle drei Mal den roten Bereich, gewinnt er nichts, sondern verliert seine 5 €. a) Mit welchem durchschnittlichen Gewinn bzw. Verlust muss ein Spieler rechnen? b) Der Erwartungswert des Spielers ändert sich in Abhängigkeit von der Größe des roten Sektors. Stelle den Zusammenhang zwischen Gewinn/Verlust des Spielers und dem Winkel dieses Sektors graphisch dar! c) Wie groß müsste der rote Sektor gewählt werden, damit das Spiel fair wird? d) Wie groß müsste der rote Sektor gewählt werden, damit der durchschnittliche Gewinn eines Spielers möglichst groß wird? Punkteverteilung: 48 ≥ Sehr gut Aufg. 1: 10 P. ≥ 44 > Aufg. 2: 14 P. (10+4) Gut ≥ 38 > Aufg. 3: 14 P. (4+5+5) Befriedigend ≥ 29 Aufg. 4: 10 P. (6+4) > Genügend insgesamt 48 Punkte möglich ≥ 23 > Nicht genügend ≥ 0 BG/BRG Kufstein Schriftliche Reifeprüfung Lösung Klasse 8D Mathematik Mag. Armin Schützinger Haupttermin 2010/2011 : a) (ohne Verwendung des TI Voyage) b² = h² + x² = = a² – y² + x² = = a² – y² + (c–y)² = y cos() a b = a² – y² + c² – 2·c·y + y² = b² = a² + c² – 2·c·y = = a² + c² – 2·c·a·cos() a h A x = a² + c² – 2·a·c·cos() B y c b) (graphisch) Maßstäbliche Zeichnung mit beliebiger Länge dZ: z.B. dZ = 6 cm Man erhält: sZ 3,75 cm D dz sz = d= d s dz s sz 6 cm 100 m 3,75 cm = = 160 m s a (rechnerisch mit Verwendung des TI Voyage) TI 100 s 100 TI 25,7 25.7 TI 28,3 28.3 TI 43,1 43.1 C b TI 29,6 TI 180 – – 108.6 TI –– 53.3 b sin() TI TI 29.6 A d sin() = dsin() sin() a sin( ) b = dsin( ) sin() .720929·d d sin() a 1.19081·d TI a² + b² – 2·a·b·cos() = s² .390635·d² = 10000 TI solve(ans(1),d) d = 159.998 or d = -159.998 Die Entfernung von A nach B beträgt 160 m. B BG/BRG Kufstein Schriftliche Reifeprüfung Lösung Klasse 8D Mathematik Mag. Armin Schützinger Haupttermin 2010/2011 : a) (ohne Verwendung des TI Voyage) orange Daten: Weltbevölkerung in absoluten Zahlen zu verschiedenen Zeitpunkten graue Daten: Zunahme der Weltbevölkerung innerhalb von zehn Jahren in absoluten Zahlen. Die Skala rechts gilt nur für die grauen Daten. Zusammenhang: Die grauen Daten entsprechen der Zunahme/Änderung der orangen Daten, also der ersten Ableitung der orangen Daten. Der höchste Punkt der grauen Statistik entspricht dem Zeitpunkt, als die Weltbevölkerung am stärksten wuchs, also dem Wendepunkt der orangen Funktion. Logistisches Wachstum, denn: Die Zunahme ist anfangs annähernd proportional zur bestehenden Weltbevölkerung, später zu einem noch vorhandenen Sättigungsmanko. Andere Wachstumsmodelle treffen nicht zu: lineares Wachstum exponentielles Wachstum P P beschränktes Wachstum P P(t) P(t) P(t) t t t b) (mit Verwendung des TI Voyage) Data-Matrix-Editor Data 1 2 3 4 5 6 c1 1804 1927 1960 1974 1987 1999 c2 1 2 3 4 5 6 F5 Calc Calculation Type … x… y… Store RegEQ to … Logistic c1 c2 y1(x) Ergebnis: y= a= b= c= d= Home: TI y1(∞) 18.6211 TI y1(2050) 11.8589 TI solve(y1(x)=10,x) x = 2034.2 Auf der Erde könnten maximal 18,62 Mrd. Menschen leben. 2050 würde die Weltbevölkerung 11,86 Mrd. Menschen betragen. Die 10 Mrd.-Grenze würde 2034 überschritten. STAT VARS a/(1+b∙e^(c∙x))+d 17.638706 1.102023E24 -.027236 .98235 BG/BRG Kufstein Schriftliche Reifeprüfung Lösung Klasse 8D Mathematik Mag. Armin Schützinger Haupttermin 2010/2011 : a) F1 = 20 20 2a 2 g = = (20 + a) 400 a F2 = 20 2a 20 2a 2b 2 20 F2 2 h = 20 + 2a b = (20 + 2a + b) 400 b2 20 F1 a (20 + a) 400 a2 + (20 + 2a + b) 400 b2 f(a,b) TI (f(a,b)) = 0 gl1 a TI (f(a,b)) = 0 gl2 b TI solve(gl2,a) TI solve(gl1,b)ans(1) 16.1803 TI ans(2)ans(1) TI cos1 5 TI TI g mit Verwendung des TI Voyage: TI h Done 400 a2 – a(a20) 2 400a + 2 400 b2 = 0 400 b2 – a= b(b2(a10)) 400b2 =0 (b2 10b 200) b 5 1 6.18034 a = 5 5 1 16.1803 b = 5 5 1/ 20 cos 5 5 1 / 20 f(5 5 1 ,5 5 1) 36 1 72 1538.84 Die mittleren Bretter müssen unter 36°, die äußeren unter 72° zur Waagrechten geneigt sein. Die maximale Querschnittsfläche beträgt ungefähr 1539 cm². b) mit Verwendung des TI Voyage: Im 3D-Modus des TI Voyage kann man Funktionen in 2 Variablen analysieren. TI f(a,b)a=x and b=y (x + 20) 400 x2 + (2x + y + 20) 400 y2 ans(1) z1(x,y) Window-Einstellungen: Done Für a = x und b = y sind nur Werte zwischen 0 und 20 sinnvoll. Für F = z werden Werte bis maximal 1600 angenommen. Im Auf- und Kreuzriss kann man mit Hilfe der Trace-Funktion die Koordinaten des höchsten Punktes ungefähr ablesen. Diese stimmen mit den berechneten Werten überein. TI Aufriss: Window-Einstellungen Graph Kreuzriss: Window-Einstellungen Graph BG/BRG Kufstein Schriftliche Reifeprüfung Lösung Klasse 8D Mathematik Mag. Armin Schützinger Haupttermin 2010/2011 : (mit Verwendung des TI Voyage) 3-stufiges Experiment mit gleich bleibenden Wahrscheinlichkeiten Binomialverteilung n=3 k Gewinn P(R=k) 3 0 ·p ·(1-p) = 1 – 3p + 3p2 – p3 0 3 0 -5 1 5 3 ·p1·(1-p)2 1 = 3p – 6p2 + 3p3 2 15 3 ·p2·(1-p)1 2 = 3p2 – 3p3 3 -5 3 ·p3·(1-p)0 3 = p3 TI -5(1–3p+3p2–p3)+5(3p–6p2+3p3)+15(3p2–3p3)–5p3 ew(p) TI ew(p) Done -30p³+30p–5 a) p= TI 120 360 = 1 3 ew(1/3) 3.889 Ein Spieler gewinnt durchschnittlich 3,89 €. EW [€] b) p 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 0 36 72 108 144 180 216 252 288 324 360 ew(p) -5,00 -2,03 0,76 3,19 5,08 6,25 6,52 5,71 3,64 0,13 -5,00 5 EW() 90 180 0,5 270 360 0,5 [°] p -5 c) TI solve(ew(p)=0,p) p=0.903 or p=0.172 (or p=-1.075) = 360°·0,903 = 325,08° = 360°·0,172 = 61,82° Das Spiel wäre dann fair, wenn der Sektor 61,8° oder 325,1° groß wäre. d) TI d(ew(p),p) ews(p) TI solve(ews(p)=0,p) TI ew(0.577) Done p=0.577 (or p=-0.577) 6.547 = 360°·0,577 = 207,85° Bei einem 207,85° großen Sektor hätte der Spieler durchschnittlich einen maximalen Gewinn von 6,55 € zu erwarten.