Inkommensurable Strecken

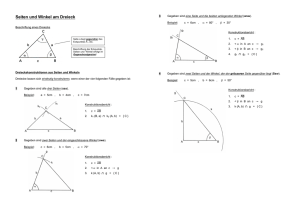
[email protected]
Inkommensurable Strecken
Zwei Zahlen a und b heißen kommensurabel (lat.: zusammen messbar), wenn sie ganzzahlige
Vielfache einer geeigneten dritten Zahl c sind. Die Zahl (Streckenlänge) c ist dann das
gemeinsame Maß, mit dem man beide Zahlen (Streckenlängen) a und b ausmessen kann,
indem man sie als ganzzahlige Vielfache von c darstellt. Gibt es kein auch noch so kleines
gemeinsames Maß c für a und b, so heißen sie inkommensurabel.
Schon um 450 v. Chr. fand der Pythagoreer HIPPASOS einen Beweis dafür, dass es für die
Diagonale und die Seite eines regelmäßigen Fünfecks kein gemeinsames Maß gibt.
Regelmäßiges Fünfeck
Im Folgenden wird unterschieden zwischen „dem alten (großen) und dem neuen (kleinen)
Fünfeck“. Es ist zunächst zu zeigen, dass Winkel, die gleich groß aussehen, es auch wirklich
sind. Zum Nachweis der Zusammenhänge zwischen den Seiten (mit der Bezeichnung a) und
den Diagonalen d beachte man geeignete Parallelogramme.
d alt  aalt  d neu und aalt  d neu  aneu bzw. d alt  aalt  d neu und aalt  d neu  aneu
Haben also die alten Diagonalen- und Seitenlängen ein gemeinsames Maß, dann haben dieses
gemeinsame Maß auch die neuen Diagonalen- und Seitenlängen. Diesen Prozess kann man zu
immer kleiner werdenden Fünfecken (der Streckfaktor ist kleiner als 0.5) fortsetzen. Dabei
wird jedes noch so kleine Maß unterschritten – Widerspruch zur Annahme eines
gemeinsamen Maßes c. (Beachtenswert ist die Nähe der Überlegungen zum Euklidischen
Algorithmus.)
d
d a
d a
Weiterhin gilt x  

 2ad  d 2  ad  a 2  x 2  x  1  0 .
a d  2  d  a  2  a  d
Das Quadrat: Untersuchung von Seiten- und Diagonalenlänge; beachte: Tangentenabschnitte
Ein weiteres Beispiel: das halbe gleichseitige Dreieck
Der Winkel BAC hat die Größe 30° und der Winkel CBA ist ein rechter Winkel. Die Strecke
ED ist ein Tangentenabschnitt (und D halbiert nicht die Strecke BC).
AC  2a und BAC  30 und AB  h  EC  2a  h und CD  4a  2h und
BD  a  4a  2h   2h  3a  a neu  2a  h und hneu  2h  3a
Wegen der Ähnlichkeit der Dreiecke ABC und DCE erhält man:
a 2a  h

 h 2  3a 2 .
h 2h  3a