SCHRIFTLICHE REIFEPRÜFUNG

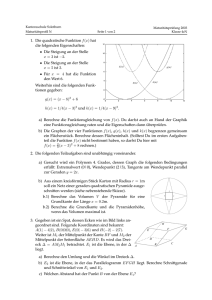
MATHEMATIK
8A, 8B
Mag. Margit Wagner, Mag. Thomas Mairold
1) DIFFERENTIAL- UND INTEGRALRECHNUNG:
Ein Trinkglas hat, wie in der nebenstehenden Abbildung zu sehen,
folgende Form:
Der äußere Teil entsteht durch Drehung eines Hyperbelsegments um die
y-Achse.
Der innere Teil entsteht durch Drehung eines Parabelsegments, das in
B(3,5/12) dieselbe Steigung besitzt wie die Tangente im Punkt
A(3,75/12) der Hyperbel, um dieselbe Achse (Maße in cm).
a) Zeige, dass die Hyperbelgleichung 256 x ²  9 y ²  2304 lautet!
b) Zeige, dass die Parabelgleichung y 
80
63
x²  329 lautet!
c) Wie viel Flüssigkeit kann in das Glas gefüllt werden?
d) Wie viele mm vom oberen Rand entfernt ist auf der Innenseite des
Glases die Markierung für ¼ Liter anzubringen?
e) Berechne das Volumen und die Masse des Glases (Dichte
Glas  2,5 g/cm³)
2) TRIGONOMETRIE / WIRTSCHAFTSMATHEMATIK:
Von einem (konvexen) fünfeckigen Grundstück ABCDE sind folgende
Maße bekannt: AB = 60 m, BC = 25 m, CD = 62 m, DE = 17 m, AE = 37
m,  =  EAB = 108°,  =  ABC = 90°.
a) Zeichne einen maßstabsgetreuen Plan des Grundstücks und berechne den Flächeninhalt!
b) Das Grundstück soll in ein flächengleiches Parallelogramm umgewandelt werden, wobei die
Seite AE und der Winkel  gleich bleiben sollen. Wie lang muss die zweite Seite AB’ sein?
c) Herr Maier kauft dieses Grundstück um 135.000 € und nimmt dafür einen Kredit zu einem
Zinssatz von 5% auf, den er in 60 vorschüssigen Monatsraten abzahlen will. Berechne die Höhe
der monatlichen Rate!
d) Nach 3 Jahren ist es ihm allerdings finanziell möglich, die Schulden zu tilgen. Wie hoch ist der
einmalige Restbetrag?
e)
3) ANALYTISCHE GEOMETRIE:
 2 
  1




Gegeben sind ein Punkt A(1/2/3) und eine Gerade g: X    6   t    4  .
 8 
 1 




a) Spiegle A an der Geraden g und zeige, dass der gespiegelte Punkt identisch mit C(7/2/9) ist.
b) Auf g liegt die Diagonale BD des Quadrates ABCD. Bestimme die Koordinaten von B und D.
c) ABCD ist die Seitenfläche eines Würfels ABCDEFGH. Bestimme die fehlenden Eckpunkte und
zwar so, dass E möglichst hoch liegen soll (d. h. die z-Koordinate des Punktes E soll möglichst
groß sein).
d) Berechne den Winkel zwischen Raumdiagonale und Seitenfläche eines Würfels!
e) Gib jeweils eine Gleichung für die Inkugel und die Umkugel des Würfels ABCDEFGH an! Wie
viel Prozent des Würfelvolumens nimmt die Inkugel ein?
4) WAHRSCHEINLICHKEITSRECHNUNG:
W1: Interpretation:
In einer Schachtel befinden sich 20 Kugeln, 6 davon sind schwarz, 14 weiß. Es werden 5 Kugeln
gezogen. Für die Berechnung der Wahrscheinlichkeit, dass unter den 5 gezogenen Kugeln genau 2
schwarze sind, haben 2 Schüler folgende Ansätze geschrieben:
5
A : P( X  2)     0,3 2  0,7 3
 2
 6    14 
  
2
3
B : P( X  2)     
 20 
5
 
Welcher Ansatz ist nach deiner Ansicht der richtige? Begründe deine Antwort und erkläre die
einzelnen "Teile" dieses Ansatzes. Gib auch eine Interpretation für den anderen Ansatz.
W2: Normalverteilungs-Beispiele sind an der Gauß-Glocken-Kurve darzustellen!
Eine Firma produziert Fußbälle mit einem Ausschuss von 4%.
Für die EM in Wien werden 250 Bälle benötigt.
a) Wie viele schlechte Bälle werden im Mittel darunter sein?
b) Mit welcher Wahrscheinlichkeit sind es mehr als 15?
c) In welchem Bereich liegt mit 90% Wahrscheinlichkeit die Zahl der
brauchbaren Bälle?
d) Wie viele Bälle müssen mindestens bestellt werden, wenn man 150
Stück benötigt und zu 99% nicht in Schwierigkeiten kommen will?
e) Nach dem Spiel können die Zuseher den Fußball um 100 € erwerben Geburtstagskinder zahlen allerdings nichts! Wie groß ist die W., dass unter 300 Interessierten
höchstens 2 Geburtstagskinder sind?
Rechne mit Binomialverteilung und überprüfe, ob sie durch die Poissonverteilung angenähert
werden kann. Vergleiche die beiden Ergebnisse!