Kapitel 6: Materie, Atome und Moleküle

Kapitel 6: Materie, Atome und
Moleküle
6.1 Die Phasen der Materie
6.2 Moleküle
6.3 Atome
6.4 Die Avogadro-Zahl
6.5 Die elektrische Ladung
6.6 Das Coulombsche-Gesetz: die elektrostatische Kraft
6.7 Das klassische Atom-Modell
6.1 Die Phasen der Materie (I)
• Vor etwa 2500 Jahren im antiken Griechenland
! Man hatte bereits ein Wissen über die physikalischen Eigenschaften der
verschiedensten Materialien.
! Man versuchte Ordnung in die Vielfalt der Materialien und ihrer
Bearbeitungsmöglichkeiten zu bringen.
! Man wollte vereinheitlichende Prinzipien finden.
! Frage nach der inneren Struktur der Materie
• Obwohl die Materie eine kontinuierliche Struktur zu haben scheint,
setzt sie sich in Wirklichkeit aus Einheiten zusammen, welche sich zu
regelmässigen Anordnungen gruppieren:
! Diese fundamentalen Grundbausteine werden als Atome bezeichnet.
! Man findet aber selten isolierte Atome. Atome bilden viel eher gebundene
Systeme, sogenannte Moleküle.
• Alle Körper (lebend wie tot) sind aus verschiedenen Gruppierungen
solcher Grundbausteine aufgebaut.
6.1 Die Phasen der Materie (II)
• Grob gesprochen erscheint Materie in drei physikalischen Zuständen
oder Phasen (wir vernachlässigen das Plasma):
! Festkörper,
! Flüssigkeiten und
! Gase
• Um die verschiedenen Anordnungen der Atome oder Moleküle in den
verschieden Phasen zu illustrieren, werden wir die drei Phasen des
Wassers diskutieren
! Eis
! Wasser
! Dampf
1. Phase: Festkörper (Eis)
• Die Moleküle sind dicht gepackt.
• Die Kräfte, die die Moleküle in festen Positionen halten, sind von etwa
der gleichen Grössenordnung wie die Kräfte, die die Atome
zusammenhalten ! Wegen diesen starken Kräften bleiben die Gestalt
und das Volumen eines Festkörpers praktisch konstant.
• Die dicht gepackten Moleküle werden sich nicht als isolierte Moleküle
verhalten.
• Regelmässigkeit der Anordnung
der Moleküle = eine wichtige
Eigenschaft von Festkörpern
• Diese Periodizität konstituiert
das Kristallgitter.
2. Phase: Flüssigkeit (Wasser)
• Moleküle in Flüssigkeiten sind durch Abstände in der Grössenordnung
der Moleküldimensionen voneinander getrennt und sie werden durch
relativ starke Kräfte zusammengehalten ! Flüssigkeiten haben ein
festes Volumen und eine geringe Kompressibilität.
• Die Moleküle weisen eine grosse Beweglichkeit auf und können
unabhängig voneinander umeinander gleiten ! Flüssigkeiten haben
keine eigene Gestalt.
3. Phase: Gase (Dampf)
• In Gasen ist die mittlere Entfernung zwischen Molekülen viel grösser als
die Ausdehnung der Moleküle ! die zwischenmolekularen Kräfte sind
viel schwächer als die Kräfte, welche die Atome in Molekülen
zusammenhalten.
• Die Moleküle behalten daher ihre Individualität.
• Die Moleküle bewegen sich ständig durch den gesamten Raum, den das
Gas einnimmt ! Gase diffundieren leicht.
• Im Dampf ist der mittlere
Abstand der Moleküle (bei
Standardbedingungen)
ungefähr 10-mal der
Durchmesser der einzelnen
Moleküle ! die Dichte des
Dampfes ist ungefähr 103 Mal
kleiner als die des Wassers.
6.2 Moleküle
• Ein Molekül besteht aus mehreren Atomkernen und einer
Gruppe von Elektronen. Die Elektronen bewegen sich um die
Kerne in solcher Weise, dass eine stabile Anordnung entsteht.
! Wenn sich ein Molekül bildet, verlieren die Atome bis zu einem
gewissen Grad ihre Identität.
• Man kennt mehrere tausend verschiedene Arten von Molekülen.
! Einige enthalten nur wenige Atome (wie z.B. das Wassermolekül)
! Andere Moleküle können bis zu mehreren hundert Atomen
enthalten, wie z.B. (1) die biologischen Moleküle (Proteine, Enzyme
und Nukleinsäuren DNA und RNA) (2) einige Polymere (Polyäthylen
oder Polyvinylchlorid PVC)
• Geometrische Muster: Die Atomkerne in Molekülen sind in
wohldefinierten geometrischen, regelmässigen Mustern
angeordnet. Diese Muster sind für jedes Molekül
charakteristisch.
Geometrie des Wasser-Moleküls
• Die drei Kerne liegen an den Eckpunkten eines Dreiecks.
• Der Abstand zwischen dem Sauerstoffkern und den
Wasserstoffkernen beträgt ungefähr 10–10 m = 1 Angström
• Der Winkel zwischen den Wasserstoffkernen ist ungefähr
104.5°.
Geometrie verschiedener Moleküle
Biologische Moleküle
• Moderne experimentelle Techniken (wie Röntgen- und
Elektronenstrahlen oder Kernspinresonanz (NMR)) haben
wertvolle Informationen über die Struktur von Molekülen
geliefert (Interdisziplinarität Physik-Biologie-Informatik).
! Diese Messungen in Zusammenhang mit fortgeschrittenen Analysen
mit Hilfe des Computers liefern völlständige drei-dimensionale
Darstellungen der Moleküle.
• Seit 1950 hat man auch viele biologische Moleküle studiert.
Heutzutage findet sich der Bereich der Biophysik und der
Molekularbiologie in starker Expansion.
! Die biologischen Moleküle zeigen eine grosse Komplexität .
• Heutzutage hat sich das Gebiet sehr entwickelt, und man
benutzt den Computer, um eine detaillierte graphische
Darstellung der Moleküle zu gewinnen.
Myoglobin-Molekül
• Kendrew und Peritz
(Nobel-Preis in Chemie,
1963): das MyoglobinMolekül wurde mit Hilfe von
Röntgenstrahlen studiert.
• Das Molekül enthält mehr als
2500 Atome.
• Die häufigsten sind
Kohlenstoff, Wasserstoff,
Sauerstoff, Stickstoff und ein
Eisenatom.
Ein Virus (http://www.mol.biol.ethz.ch)
6.3 Atome
• Atome sind nicht elementar, sondern besitzen selbst eine innere
Struktur:
! Atome können in sogenannte Elementarteilchen getrennt werden.
! Drei Arten von Elementarteilchen sind besonders wichtig: das Elektron, das
Proton und das Neutron.
• Experimentell beobachten wir:
! Elementarteilchen verhalten sich wie “kleine Körper” mit bestimmter Energie
und bestimmtem Impuls.
! Die Elementarteilchen werden miteinander wechselwirken: während diesen
Wechselwirkungen werden die Gesamtenergie und der Gesamtimpuls immer
erhalten.
• Die Elementarteilchen werden deshalb oft als “kleine Kugeln”
dargestellt werden, die miteinander stossen, wie in einem Billardspiel.
Protonen, Neutronen und Elektronen
mp = (1,67262158 ± 0,00000013) ! 10 "27 kg
• Massen:
mn = (1,67492716 ± 0,00000013) ! 10
"27
kg
me = (9,10938188 ± 0,00000072) ! 10 "31 kg
• Protonen ! Neutronen = NUKLEONEN
! Nukleonmasse
#27
mN ! 1,67 " 10
kg
• Wieviele Nukleonen sind in einem Gramm enthalten?
"3
1 g
10 kg
23
N=
!
!
6
#
10
mN 1,67 # 10 "27 kg
• In gewöhnlicher Materie:
Ne = N p ! Nn
! Die Nukleonen tragen den grössten Teil der Masse eines Körpers.
Die Elektronen tragen weniger als ein Promille zur Masse bei.
Das Elektronvolt (eV)
• Eine praktische Einheit für die Energie der Teilchen, wenn wir
Elementarteilchen wie Elektronen oder Protonen betrachten.
! Das Elektronvolt ist ein Mass der Energie.
! Die Umrechnung von Elektronenvolt in Joule ist die folgende
1 eV = 1,60217 ! 10
"19
J
• Beispiel: Energie der Ruhemasse des Protons, Neutrons und Elektrons
(
m p c = 1, 67 ! 10
2
"27
)(
kg 3 ! 10 m / s
8
)
2
= 1, 5 ! 10 "10 J
1, 5 ! 10 "10
6
=
eV
#
938
!
10
eV = 938 MeV # 1 GeV
"19
1, 602 ! 10
mp c 2 = 938,271998 ± 0,000038 MeV
Genaue
Messungen
mn c 2 = m p c 2 + (1,2933318 ± 0,0000005 MeV )
me c 2 = 0,510998902 ± 0,000000021 MeV
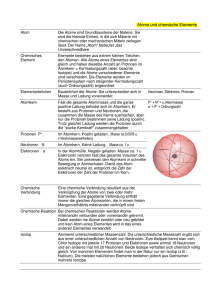
Das Atom und die Elemente
• Zur Zeit kennen wir 114 Elemente, von denen 92 in der Natur
vorkommen.
• Jedes Atom ist charakterisiert durch:
! Z Protonen und ebenso viele Elektronen
! N Neutronen
• Definitionen:
! Die Protonenzahl = Ordnungzahl Z
A=Z+N
! Die Gesamtzahl der Protonen und Neutronen ist die Massenzahl A
• Alle Atome mit der gleichen Ordnungszahl gehören zum gleichen
chemischen Element
• Im Jahr 1870 hat Mendelejev die Elemente im Periodensystem der
Elemente klassifiziert. In diesem System wurden die Atome als
Funktion ihrer Ordnungszahl und durch ihre chemischen Eigenschaften
organisiert.
Struktur der Atome
• Ein Atom besteht aus einem elektrisch positiv geladenen Kern
aus Nukleonen (Protonen, Neutronen) mit einer elektrisch
negativ geladenen Elektronenhülle darum herum.
• Typ. Durchmesser eines Kerns
"15
dKern ! 1 fm = 10
m
• Typ. Abstand der Elektronen vom Kern
"10
rElektron ! 1 Å = 10
Kern
m = 100000 fm
Elektronen
Struktur der Atome
• Die Elektronen sind in Schalen um den Kern angeordnet, die
umso mehr Elektronen aufnehmen können, je weiter aussen sie
sich befinden.
! Z.B. enthält die erste Schale maximal 2 Elektronen, die zweite 8,
die dritte 18 und die vierte 32, ...
Anordnung der Elektronen um den Kern in einigen einfachen
Atomen (Helium, Neon, Argon und Krypton)
Elektronenhülle
• Obwohl Elementarteilchen als “kleine Kugeln” dargestellt werden
können, können die Elektronen um den Kern nicht mit Hilfe einer Bahn
beschrieben werden!
! Eine Berechnung der “räumlichen Verteilung der Elektronen” muss mit Hilfe
der sogenannten Quantenmechanik durchgeführt werden.
• Da die Bahnen der Elektronen nicht wohldefiniert werden können,
zeigen die dunklen Bereiche diejenigen Zonen an, die mit grosser
Wahrscheinlichkeit mit Elektronen besetzt sind.
Die richtige Berechnung der
Elektronenkonfigurationen und
die damit mögliche Deutung
der chemischen Eigenschaften
gehörten zu den grossen
Erfolgen der
Quantenmechanik.
1,5 Å
Die Isotope
• Atome mit der gleichen Ordnungszahl Z können verschiedene
Massenzahl A besitzen.
! Isotope = Atome mit gleicher Ordnungszahl Z aber verschiedener
Massenzahl A.
• Zur Zeit kennt man mehr als 1300 verschiedene Isotope.
Kerne der Isotope des
Wasserstoffs:
6.4 Die Avogadro-Zahl
•
Materie besteht aus einer sehr grossen Zahl von Atomen oder Molekülen. Ein
Gramm enthält !6x1023 Nukleonen.
•
Die Avogadro-Zahl = Anzahl der
12C
Atome in genau 12g Kohlenstoff
12C
0,012kg
N A = 6,02213665 ! 10 "
6m p + 6mn + 6me
23
•
Eine praktische Einheit, um die Menge von Atomen oder Molekülen zu
definieren:
! Stoffmenge = Anzahl der Mole =
N
n!
NA
Anzahl Atome
oder
Moleküle
• 1 Mol einer beliebigen Substanz enthält NA (die Avogadro-Zahl) Atome
oder Moleküle
• Molare Masse m = Masse eines Mols einer Substanz
M = nm
Gesamtmasse der Substanz
6.5 Die elektrische Ladung
• Elektronen, Protonen, Neutronen werden durch ihre physikalischen
Eigenschaften unterschieden.
• Sie werden durch zwei unabhängige und fundamentale Eigenschaften
charakterisiert:
! Ruhemasse m0 und elektrische Ladung q
• Die elektrische Ladung (wie die Ruhemasse) ist wirklich eine
fundamentale Eigenschaft der Materie
• Elementarteilchen, die elektrisch geladen sind, werden durch die
elektromagnetische Wechselwirkung wechselwirken.
• Diese Wechselwirkung ist sehr wichtig:
! Sie hält ein Atom zusammen
! Sie ist verantwortlich für die Bindung einzelner Atome in Molekülen und für
die Wechselwirkungen zwischen den Molekülen.
! Die dichte Packung von Atomen in Festkörpern und die Wechselwirkungen
zwischen den Molekülen von Flüssigkeiten sind von der elektrischen
Wechselwirkung beherrscht ! die Phasen der Materie sind durch sie
bestimmt.
Die Ladungen der Elementarteilchen
• Experimentell beobachten wir
1. Elektronen sind “elektrisch negativ geladen”
" jedes Elektron besitzt eine negative elementare Ladung
qe = !e
2. Protonen sind “elektrisch positiv geladen”
" Das Proton hat genaue die gleiche Ladung wie das Elektron,
aber mit entgegengesetztem Vorzeichen
q p = +e
3. Neutronen sind “elektrisch ungeladen”, d.h. neutral
qn = 0
Eigenschaft der Ladung (I)
1. Ladungquantisierung:
! Die gesamte Ladung eines beliebigen Körpers kommt immer nur als
Vielfaches der Elementarladung “e” vor (die ist Ladung quantisiert)
2. Einheit der Ladung:
! Die SI-Einheit ist das Coulomb (C) :
e ! 1,60217 " 10
! Definition des Elektronvolts:
#19
C
1 eV = (e) J = 1,60217 ! 10 "19 J
! d.h. das Elektronvolt entspricht einer Energie von e Joule.
! (Kap. 10: das Elektronvolt ist gleich der Energiezunahme, wenn ein
Teilchen mit der Elementarladung e durch einen
Potentialunterschied von 1 Volt beschleunigt wird).
Eigenschaft der Ladung (II)
3. Addition der Ladung:
! Die Gesamtladung eines Körpers wird als die Summe der einzelnen
Ladungen bestimmt
! Ein neutraler Körper hat eine verschwindende Gesamtladung. D.h.,
er besitzt eine gleiche Anzahl von positiven und negativen Ladungen
! Atome sind daher elektrisch neutral.
! In gewöhnlicher Materie: Anzahl von Protonen und Elektronen gleich
! die positiven und negativen Ladungen kompensieren sich und die
gewöhnliche Materie ist elektrisch neutral.
4. Ladungserhaltung:
! Die Gesamtladung eines Systems wird immer erhalten. Wir kennen
keine Ausnahme dafür. Wie im Fall der Impulserhaltung muss jede
Reaktion, die in der Natur geschieht, die Gesamtladung erhalten
! Die Gesamtladung des Universums ist eine Konstante: elektrische
Ladungen können nie erzeugt oder vernichtet werden.
Eigenschaft der Ladung (III)
• Leiter und Nichtleiter:
! Elektrische Leiter: Stoffe, in denen sich Elektronen frei bewegen können.
Z.B. Metalle
! Nichtleitern: die Elektronen fest an die einzelnen Atome und deren nähere
Umgebung gebunden. Z.B. Holz, Glas, ...
• Elektrostatische Aufladung von Körpern
! Man kann (freie) Elektronen zu einem Körper bringen oder wegnehmen.
• Anzahl von Elektronen > die der Protonen: der Körper ist negativ geladen.
• Anzahl von Elektronen < die der Protonen: der Körper wird positiv geladen.
! Graphische Darstellung:
Demonstrationsexperiment
Das Elektroskop
• Elektroskop = Apparat, mit welchem gemessen werden kann, ob ein
Körper elektrisch geladen ist.
• Bemerkung: Das Elektroskop unterscheidet das Vorzeichen der
Ladung nicht, es zeigt nur, ob die Kugel geladen ist oder nicht
Kugel wird geladen
Gleichnamige
Ladungen stossen
sich ab
Die zwei „Beine“ sind Leiter (metallisch)
6.6 Die elektrostatische Kraft
• Die Kraft zwischen ruhenden elektrischen Ladungen: Experimente von
Coulomb und anderen Forschern führten zum Coulombschen Gesetz
! Zwei Punktladungen q1 und q2, die sich im Abstand r voneinander befinden,
üben eine Kraft aufeinander aus. Die Kraft wirkt entlang der
Verbindungslinie zwischen q1 und q2, und ist umgekehrt proportional zum
Quadrat des Abstandes r der Ladungen und proportional zu deren Produkt.
• Demonstrationsexperiment: Coulombsches Gesetz mit Drehwaage
! Die Abstossung zwischen zwei geladenen Kugeln wird gemessen.
! Sie ist umgekehrt proportional zum Quadrat des Abstands der Kugeln.
Das Coulombsche Gesetz
Ruhende elektrische Ladungen:
Gleichnamige Ladungen stossen sich
ab, ungleichnamige ziehen sich an.
q1q2 > 0 !
abstossend
q1q2 < 0 !
anziehend
Elektrostatische Kraft:
!
!
q1q2 r12
F12 = K 2
r12 r12
K ist eine Konstante,
die die benötigte
Einheit besitzt, um das
Produkt zweier
Ladungen geteilt durch
das Quadrat einer
Länge in die Einheit
der Kraft umzuwandeln
Proton-Proton, Elektron-Elektron, Proton-Elekton
Konstante K
• Die Konstante K wird durch die Definition der Ladung bestimmt.
• Heutzutage wird die Einheit der Ladung durch die Definition des
Ampère definiert (Siehe Kap. 1.2). Das Coulomb wird nicht als
fundamentale Einheit angenommen.
• Aus der Definition des Ampère folgt:
! Das Coulomb ist die Ladung, welche eine gleiche Ladung in der
Entfernung von 1 m im Vakuum mit einer Kraft von 10–7c2 Newton
(wobei c die Lichtgeschwindigkeit in m/s ist) abstösst.
1[C]1[C ]
!7 2
10 c [ N ] = K
(1[m]) 2
K ! 10
"7
(3 # 10 )
8 2
2
[ Nm ]
[C ]
2
"
Nm / C
2
K = 10 !7 c 2
! 9 # 10
2
9
2
Nm / C
2
Dielektrizitätskonstante des Vakuums "0
• Die Konstante K wird als Funktion der sogenannten
Dielektrizitätskonstante des Vakuums oder elektrische
Feldkonstante "0 definiert (Die Bedeutung dieser Definition wird
im Kap. 10 besser erklärt):
1
K=
4!" 0
!
!
1 q1q2 r12
F12 =
4!" 0 r12 2 r12
• Die elektrische Feldkonstante "0 hat den Wert
!0 " 8,854 # 10
$12
2
$1
C N m
$2
Gravitation versus elektrostatische Kraft
!
!G
m1m2 r12
F12 = !G
2
r12 r12
G = 6,67 #
10–11
Nm2/kg2
proportional zum Produkt der Massen
!
!
q1q2 r12
F12 = K 2
r12 r12
K ! 10 "7 c 2 ! 9 # 109 Nm 2 / C 2
proportional zum Produkt der Ladungen
Gleichnamige Ladungen stossen sich
ab, ungleichnamige ziehen sich an.
Immer anziehend
umgekehrt proportional zum
Quadrat des Abstandes
q1q2 > 0 !
q1q2 < 0 !
abstossend
anziehend
umgekehrt proportional zum
Quadrat des Abstandes
Gravitation versus elektrische Kraft
• Im Vergleich zur Gravitationskraft ist die elektrische Kraft sehr
stark.
• Das Verhältnis der elektrischen Kraft zur Gravitationskraft für
das Elektron und Proton ist (unabhängig vom Abstand, weil
beide Kräfte proportional zu r–2 sind)
1 e2
Fe
4!"0 r 2
1
e2
=
=
me m p 4!" 0 G me m p
FG
G 2
r
9 $ 109
(1,602 $ 10%19 ) 2
39
#
#
2
$
10
6,67 $ 10%11 (9,10 $ 10%31)(1,67 $ 10 %27 )
Gravitation versus elektrische Kraft
•
Nur wenn ein Körper elektrisch neutral ist, ist seine Gravitationskraft wichtig.
! kein Gleichgewicht zwischen positiven und negativen Ladungen ! die elektrische Kraft
ist immer viel grösser als die Gravitationskraft
•
Die elektrische Ladung des Elektrons und des Protons kompensieren sich exakt.
Eine sehr wichtige Eigenschaft der Natur: damit sind Atome elektrisch neutral !
! Die Bewegung makroskopischer Körper (wie z.B. der Mond, die Erde, die Planeten, die
Galaxien oder ein frei fallender Ball in der Nähe der Erdoberfläche) ist von der
Gravitation beherrscht, während die innere Struktur dieser Körper (z.B. ihre Phase
(fest, flüssig, ...), ihre Härte, ihre Weichheit, usw...) von der elektrischen Kraft
bestimmt wird.
•
Wegen der elektrischen Neutralität der gewöhnlichen Materie sind die Rollen der Gravitation
und der elektrischen Kraft im Universum unterschiedlich.
•
Die Kompensation der Ladungen des Elektrons und des Protons ist ein Rätsel der modernen
Physik.
! Wir kennen keine “Erklärung” dafür.
! Was man sucht, ist eine überprüfbare Theorie, die die Kompensation der Ladung des Elektrons und
des Protons als eine Folge von grundlegenden Prinzipien erzwingt.
Die elektrische potentielle Energie
•
Wir suchen nun die potentielle Energie der elektrischen Kraft.
•
Die potentielle Energie der Gravitationskraft (Kap. 4) mit dem Nullpunkt im
Unendlichen
•
!
!
GMm r
FG = ! 2
r
r
Mit einer ähnlichen Herleitung: die potentielle Energie der elektrischen Kraft ist
!
F12 =
•
"
!
GMm
E pot (r ) = !
r
G
!
!
F = ! "E pot
!
1 q1q2 r12
4!" 0 r12 2 r12
#
!
E pot (r ) =
e
1 q1q2
4!" 0 r
Wenn die zwei Ladungen unendlich weit voneinander entfernt sind, spüren die
Ladungen einander nicht. In diesem Fall verschwindet ihre elektrische potentielle
Energie.
•
Wenn sich die Ladungen nähern, kann die elektrische potentielle Energie
abnehmen oder zunehmen. Die Situation hängt vom Vorzeichen des Produkts
der Ladungen ab.
6.7 Das klassische Atom-Modell
• Historisch dachte man, dass Atome Elektronen und Protonen enthalten.
! Die Gesamtbewegung dieser Elektronen und Protonen konnte aber nicht
gelöst werden. Man brauchte ein Atom-Modell.
• Atommodell von Thompson
! Die Atome werden als Kugeln mit einer gleichmässig verteilten positiven
und negativen Ladung betrachtet.
• Streuexperiment von Rutherford (1910): H. Geiger, E. Marsden
und E. Rutherford führten eine Reihe von Streuexperimenten mit $Teilchen durch.
! Ein $-Teilchen ist ein schweres Teilchen (ungefähr 7400-mal die Masse des
Elektrons). Es enthält zwei Protonen und zwei Neutronen.
• Mit diesen Experimenten bewies Rutherford, dass ein Atom aus einem
positiv geladenen Kern mit einer äusseren Elektronenhülle besteht.
Rutherford Streuexperiment
Ein paralleler Strahl von $Teilchen wurde senkrecht
auf eine 0,4µm dünne
Goldfolie gerichtet. Dabei
fanden Stösse zwischen
den $-Teilchen und den
Gold-Atomen statt.
Während des Stosses
wurde Impuls zwischen
den $-Teilchen und den
Atomen übertragen
Streuung des $-Teilchens
• Experimentell beobachtete Rutherford, dass die meisten $-Teilchen in
Vorwärtsrichtung gestreut wurden. Eine geringe Anzahl wurde nach
rückwärts gestreut. Nach der Impulserhaltung (d.h. Teilchen
=Kugeln) muss die Masse des Stosspartners viel grösser als die des $Teilchens sein.
! Rutherford stellte daraufhin sein Atommodell vor, bei dem ein positiv
geladener massereicher Kern von einer fast masselosen Hülle von negativ
geladenen Elektronen umgeben ist.
Elektrische Abstossung im Kern
• Protonen und Neutronen eines Atoms sind in seinem Kern
konzentriert. Die elektrische Abstossung zwischen zwei Protonen
im Kern ist viel grösser als ihre Anziehung aufgrund der
Gravitationskraft:
! Eine zusätztliche Wechselwirkung, die sogenannte starke
Wechselwirkung, hält Protonen im Kern zusammen, trotz ihrer
elektrischen Abstossung.
• Die starke Wechselwirkung wirkt zwischen Protonen und
Neutronen, und hat eine kleine Reichweite (in der
Grössenordnung des Kerndurchmessers).
! Wenn Protonen oder Neutronen sich in einem Abstand kleiner als
einige Kerndurchmesser voneinander befinden, werden sie dank der
starken Kraft zusammengebunden.
Spektroskopie von isolierten Atomen
•
Ende des 19. Jahrhunderts: viele experimentelle Daten über die
Linienspektren von isolierten Atomen und Molekülen.
•
Linienspektren = Charakteristika, mit denen man Atome oder Moleküle
identifizieren kann.
•
Durch die Untersuchung der Linienspektren wird die Struktur der Atome
aufgeklärt.
•
Die Spektren werden mit Hilfe eines Prismas analysiert. Das Prisma zerlegt das
Licht in Farben (d.h. Frequenzen)
Bildschirm
Zunehmende
Frequenz
Frequenzen des sichtbaren Lichts
• Licht einer bestimmten Farbe entspricht einer harmonischen
elektromagnetischen Welle bestimmer Wellenlänge
1 " kc 2# c
c
Frequenz: ! = =
=
=
=
T 2# 2#
$ 2# $
Zwei Arten von Spektren
• Emissionspektrum: die Wellenlänge des vom Atom emittierten
Lichtes.
! Das Atom muss angeregt werden (in der Praxis verwendet man ein heisses
Gas) und das emittierte Licht wird analysiert (z.B. mit einem Prisma, das das
Licht in Farben zerlegt).
• Absorptionsspektrum: die Wellenlänge des vom Atom absorbierten
Lichtes.
! Man verwendet weisses Licht und schickt es durch die Atome (in der Praxis
durch Dampf) des gewählten Elements. Die Absorption erscheint als
schwarze Linie (fehlendes Licht).
Absorption von Natriumdampf
• Demonstrationsexperiment: Zwei Kohlestäben mit einem mit
Natriumkarbonat gefüllten Loch.
! Ein Lichtbogen wird mit Hilfe eines elektrischen Stromes erzeugt.
! Die Elektroden emittieren wegen ihrer hohen Temperatur ein quasikontinuierliches Spektrum. Gleichzeitig verdampft das Natrium.
! Die Natrium-Absorptions-Linie ist sichtbar
Spektrum von atomarem Zink
• Demonstrationsexperiment: Eine Messing- und eine Kohlelektrode
werden verwendet, um einen Lichtbogen zu erzeugen. Wir beobachten
die einzelnen Emissionslinien des Zinks.
Spektrum des atomaren Wasserstoffs
• Die Wellenlängen der Linien im Spektrum des atomaren Wasserstoffs
waren schon seit langem bekannt. Das Wasserstoff-Atom ist das
einfachste Atom zu beschreiben (Ein Proton und ein Elektron)
• Die beobachteten Linien des atomaren Wasserstoffs:
Wellenlänge %
Balmer-Rydberg-Formel
• Es gab eine sehr genaue empirische Formel, die zuerst 1885 von
Balmer, einem Schweizer Lehrer an der Universität Basel, angegeben
wurde. Die Formel wurde später von Rydberg verbessert:
1
1%
# 1
= R$ 2 " 2 &
!
m
n
R = Rydberg-Konstante
c
1'
$ 1
! = = Rc & 2 # 2 )
%m
"
n (
Balmer " Rydberg " Formel
R = 1,097 ! 10
7
m
"1
Rc ! (1,097 " 107 m #1)( 3" 10 8 m / s)
! 3,29 " 10
15
Hz
Für ein festes m liefert die Balmer-Rydberg-Formel eine Serie
von Linien mit Wellenlängen , die sich nähern, wenn die Zahl n
zunimmt.
Für m=2: die Balmer-Serie
1
1&
# 1
= R% 2 " 2 (
$m
!
n '
n=5, 6, …
n=4
n=3
Die Linien nähern
sich , wenn die Zahl n
zunimmt.
Wellenlänge %
Lyman- und Paschen-Serie
Andere Linienspektren: die sogenannte Lyman-Serie und Paschen-Serie, die den
Zahlen m=1 und m=3 entsprechen. Sie sind nicht sichtbar!
m=3
m=1
Das Bohrsche Atom-Modell
• Niels Bohr (1913): Die Theorie des einfachsten Atom-Systems
(Wasserstoff-Atom mit Z=1, A=1)
! Weil die Form der elektrischen Kraft ähnlich derjenigen der Gravitationskraft
ist, wird man mit Hilfe der klassischen Mechanik voraussagen, dass das
Elektron sich um das Proton bewegt wie ein Planet um die Sonne.
m p ! 2000me
Annahme: das Proton befindet sich in Ruhe und das
Elektron bewegt sich um das Proton
Energie des Atoms (I)
• Die Energie des Atoms ist
E = Ekin + E pot,interne
1 !2
! me ve + E pot,elektrische Kraft
2
• Die elektrische potentielle Energie (Proton und Elektron ziehen einander
an)
2 !
!
1 e r
Fe = !
4"#0 r 2 r
$
2
!
1
e
E e pot ( r ) = !
4"#0 r
Entfernung des
Elektrons
2
1 !2
1 e
E = mev e !
2
4"# 0 r
Energie des Atoms (II)
• Annahme: Wasserstoff & symmetrisch & Bahn ist ein Kreis
!2
!
mev e
1 e2
Fe =
=
r
4!" 0 r2
#
!2
me v e =
1 e2
4!" 0 r
1 # 1 e2 &
1 e2
1 # 1 e2 &
E(r) = %
)
=) %
2 $ 4!" 0 r (' 4!" 0 r
2 $ 4!" 0 r ('
• Diese Gleichung entspricht der Energie des Systems, wenn das
Elektron sich auf einem Kreis mit Radius r um das Proton bewegt
1 $ 1 e2 '
E(r) = ! &
)
2 % 4"# 0 r (
• Da die Energie einen negativen Wert besitzt, ist das Elektron-ProtonSystem “gebunden”. Das Elektron wird ständig um das Proton kreisen.
• Beschreiben diese Ergebnisse die Eigenschaften des Wasserstoffatoms?
Nicht genau. Wie können die Linienspektren erklärt werden?
Geniale Postulate von Niels Bohr (1913)
1. Postulat der stationären Zustände: Bohr nahm
an, dass das Wasserstoffatom in einer Anzahl von
stationären Zuständen bestimmter Energie existieren
kann. Diese Annahme ist in grossem Widerspruch
zur klassischen Mechanik.
2. Postulat der Frequenz: Bohr postulierte, dass das
Wasserstoffatom Licht (Strahlung) nur emittieren
oder absorbieren kann, wenn das Atom von einem
stationären Zustand in einen anderen übergeht.
Dabei ist die Frequenz des Lichts zur Differenz der
Energien dieser beiden Zustände proportional.
Zustandsübergang
• Geht ein Atom von einem Anfangszustand mit der Energie En in einen
Endzustand mit der (niedrigeren) Energie Em über, so ist die Frequenz
des emittierten Lichts gleich
1
! = (E n " E m )
h
wobei h die sogenannte Plancksche Konstante ist, die eine Energie in
eine Frequenz umwandelt (die Einheit der Konstante ist ein Produkt von
Energie und Zeit, d.h. J.s)
Energie des Wasserstoff-Atoms
• Im Vergleich mit der empirischen Balmer-Rydberg-Formel
1
1%
# 1
! = (E n " E m ) = Rc $ 2 " 2 &
h
m
n
En
hcR
" 1$
= Rc# ! 2 % & E n ' ! 2
h
n
n
n=1,2,3,..
• Die Energie der Elektronenbewegung im Atom ist quantisiert.
! Im Rahmen der klassischen Mechanik sind den möglichen Werten
für die Energie des Elektrons in einem Atom keine Grenzen gesetzt.
! Im Gegensatz dazu zeigen die Linienspektren, dass die Energie
eines Elektrons in einem Atom auf bestimmte Werte beschränkt ist!
Für den Fall des Wasserstoffatoms findet man experimentell, dass
die Energie des Elektrons von der folgenden Form ist:
13, 6 eV
En = !
n = 1, 2, 3,...
2
n
hcR ! 13, 6 eV ! 2,177 " 10 #18 J
Damit ist der Wert der Planckschen Konstante gleich
2,177 " 10#18 J
2,177 " 10 #18 J
h!
!
cR
( 3" 10 8 m / s)(1,097 " 107 m #1 )
! 6,63" 10 #34 Js
Erlaubte Energieniveaus des Wasserstoffatoms
Werte der Energie der
stationären Zustände:
13, 6 eV
En = !
n2
n = 1, 2, 3,...
Der Übergang zwischen zwei
erlaubten Werten der Energie
erzeugt Licht mit bestimmten
Frequenzen, die den bekannten
Serien entsprechen
ultraviolett
sichtbar
infrarot
1
! = (E n " E m )
h
Weitere Erklärung von Bohr
• Niels Bohr behauptete, dass seine Postulate erzwingen, dass die
möglichen Werte des Drehimpulses des Elektrons durch den
folgenden Ausdruck gegeben sind:
nh
L = rp = rm ev !
= n!
2"
wobei
n = 1,2,3,...
! die folgende Konstante ist
h
#34
!=
= 1, 05045 " 10 Js
2!
• Der Drehimpuls eines Elektrons in einem Atom ist auf
bestimmte Werte beschränkt!
Energie des Elektrons
2
2
1
e
m
e
2
2 2 2
2
e
L
=
r
m
v
=
r
m
=
r
• Weil
e e
e
4!" 0 r 4!" 0
gilt
• Mit
1 $ 1 e2 '
1 me e 4 1
E(r) = ! &
)=!
2 % 4"# 0 r (
2 (4"# 0 )2 L2
L ! n!
n = 1,2,3,...
4
die Energie
hcR
En ! " 2
n
1 mee
1
En = !
2
2 2
2 (4"# 0 ) n !
En n 2
me e 4
1
R=!
=
2
3
hc
4" ( 4"# 0 ) ! c
Radius der Elektron-Bahnen
• Es gilt:
4!"0 L2 # 4!" 0 ! 2 & 2
2
r=
=
n
)
a
n
%$ m e 2 ('
0
mee 2
e
4!" 0 !
%11
a0 =
#
5,292
$
10
m
2
mee
2
wobei
Der Bohrsche Radius
• Der Radius r = a0n2 darf nicht zu genau genommen werden.
Man sollte ihn nur als einen Hinweis auf die Grössenordnung des
Bereichs werten, in welchem das Elektron mit grösster
Wahrscheinlichkeit gefunden wird.
4!"0 L2 # 4!" 0 ! 2 & 2
2
r=
=
n
)
a
n
%$ m e 2 ('
0
mee 2
e
hcR
En = ! 2
n
c
1
= " = ( En # E m )
!
h
s
diu
Ra
Das Elektron ändert “seinen Index” von n zu m, verliert Energie und
ändert seinen Radius. Es emittiert Licht bestimmter Frequenz, die durch
die Energiedifferenz bestimmt wird.
Zustand eines Elektrons im Atom
• Zusammenfassend werden der Radius, der Drehimpuls und die Energie
des Elektrons vollständig durch eine Zahl n bestimmt. D.h., der
Zustand des Elektrons wird durch n bestimmt.
+ # 4!" ! 2 &
2
2
0
-r = %
n
)
a
n
0
- $ me e 2 ('
nh
= n!
,L =
2!
# 1 m e4 & 1
e
-E n = * %
2 2(
2
2
n
$ (4!" 0 ) ! '
.
n = 1,2,3,...
Die Zahl n wird als Hauptquantenzahl bezeichnet. Wir
werden später sehen, dass es zusätzliche Quantenzahlen gibt,
die den Zustand des Elektrons definieren.