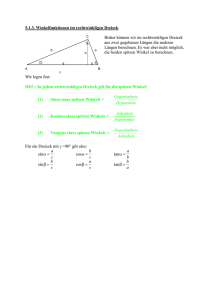
Grundbegriffe in rechtwinkligen und gleichschenkligen Dreiecken

Konstruktionen und Berechnungen
an rechtwinkligen und gleichschenkligen Dreiecken
Eine Werkstatt
In den kommenden 5 Wochen werden Sie individuell und in Ihrem Tempo
Konstruktions- und Rechenverfahren im Zusammenhang mit rechtwinkligen und
gleichschenkligen Dreiecken erlernen. Die Lernform, die ich Ihnen dazu anbiete, ist der
Werkstattunterricht. Dabei wird der gesamte Stoff in einzelne Posten unterteilt. Die
Reihenfolge, in der Sie die Posten bearbeiten, ist nur so weit festgelegt, als es für
einen sinnvollen Aufbau unumgänglich ist. Somit haben Sie (fast) immer eine grosse
Auswahl, welchen Posten Sie als nächstes bearbeiten wollen. Um Ihre Wahl zu
erleichtern, liegen alle Posten (bis auf den Prüfungsposten) zur Ansicht auf dem
Lehrerpult.
Wie die einzelnen Posten voneinander abhängen, ist auf Ihrem Werkstattpass
dargestellt. Sie können dort erkennen, dass auch die Prüfung ein Posten ist, und dass
Sie nicht alle Posten bearbeiten müssen, um die Prüfung schreiben zu können. Die
Posten, die nicht Voraussetzung für die Prüfung sind, sind freiwillig und behandeln
grösstenteils Bezüge des Themas zu anderen Fächern wie Deutsch, Geschichte und
Geographie.
Das Thema wird am 13. März schriftlich geprüft.
Damit Sie sich in der Freiheit, die Ihnen auf diese Art gewährt wird, zurecht finden,
gelten die folgenden Regeln:
1. Sie erhalten erst dann einen neuen Posten, wenn Sie einen anderen Posten fertig
bearbeitet und mir zur Kontrolle vorgelegt haben.
2. Ein neu gewählter Posten darf keine Posten voraussetzen, die Sie noch nicht
bearbeitet haben. Um den Überblick zu behalten, erhalten Sie im Werkstattpass für
jeden bearbeiteten Posten eine Bestätigung.
3. Grundsätzlich steht Ihnen der Arbeitsort frei. Zumindest am Anfang und Schluss
jeder Lektion (bzw. Doppellektion) müssen Sie jedoch im Klassenzimmer
erscheinen.
4. Im Klassenzimmer wird ausschliesslich ruhig und konzentriert gearbeitet.
Copyright © 2009 Michael Weiss.
Permission is granted to copy, distribute and/or modify this document under the terms of
the GNU Free Documentation License, Version 1.3 or any later version published by the
Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no
Back-Cover Texts. A copy of the license is included in the section entitled "GNU Free
Documentation License".
Grundbegriffe in rechtwinkligen und gleichschenkligen Dreiecken
Rechtwinklige Dreiecke
In rechtwinkligen Dreiecken heisst die Seite, die dem rechten Winkel gegenüber liegt,
Hypotenuse. Die anderen beiden Seiten heissen Katheten.
Hypotenuse
Kathete
.
Kathete
Die Seiten werden mit den Buchstaben a, b und c beschriftet, die Ecken mit A, B und
C, die Winkel mit α und β (γ ist der rechte Winkel und wird mit einem Punkt
bezeichnet). Dabei gelten folgende Regeln:
•
•
•
c ist immer die Hypotenuse
a, b und c umlaufen das Dreieck im sogenannten positiven Drehsinn, das bedeutet
im Gegenuhrzeigersinn.
A und α liegen gegenüber von a, B und β liegen gegenüber von b. C liegt dort, wo
der rechte Winkel liegt.
Beispiel:
B
B
β
β
a
C
c
c
b
richtig
.
α
A C
b
falsch
.
α
a
A
Warnung:
Man stösst immer wieder auf anders angeschriebene Dreiecke. Daher
sollten Sie Formeln (z.B. a2 + b2 = c2) nicht mit Buchstaben auswendig lernen, sondern
mit Worten. Im folgenden rechtwinkligen Dreieck ist a 2 + b2 = c2 falsch:
B
β
a
b
C
.
c
α
Wenn Sie sich dagegen merken: (1. Kathete) 2 + (2. Kathete)2 = (Hypotenuse)2, können
Sie sofort sagen, dass in diesem Dreieck die richtige Beziehung b 2 + c2 = a2 ist.
Wenn man sich entweder auf α oder auf β bezieht, kann man bei den Katheten
zwischen Ankathete und Gegenkathete unterscheiden:
•
•
Bezogen auf α ist b die Ankathete, weil b an
weil a auf der gegenüberliegenden Seite von
Bezogen auf β ist a die Ankathete, weil a an
weil b auf der gegenüberliegenden Seite von
B
B
β
c
Gegenkathet
e
C
α anliegt, und a ist die Gegenkathete,
α liegt.
β anliegt, und b ist die Gegenkathete,
β liegt.
c
Ankathete
.
α
Ankathete
A
C
.
A
Gegenkathet
e
B
Bei rechtwinkligen Dreiecken meint man mit der
Höhe immer die Höhe hc auf c, also das Lot von C
auf c. Die Höhe ha auf a ist nämlich die Seite b,
und die Höhe hb auf b ist die Seite a. Statt h c nennt
man die Höhe auf c daher einfach h.
β
a
C
.
c
h
.
α
b
Gleichschenklige Dreiecke
In einem gleichschenkligen Dreieck sind zwei
Seiten gleich lang. Diese Seiten heissen Schenkel
und werden mit dem Buchstaben s bezeichnet. Die
dritte Seite heisst Basis und wird mit a
angeschrieben. Die Ecken bekommen keine
Namen. Die beiden Winkel zwischen einem
Schenkel und der Basis sind gleich gross und
heissen beide β. Der Winkel zwischen beiden
Schenkeln heisst α.
Ein
gleichschenkliges
Dreieck
hat
eine
Symmetrieachse. Diese ist gleichzeitig die Höhe
auf a. Diese Höhe nennt man meistens einfach h,
weil
die
Höhen
auf
die
Schenkel
eher
uninteressant sind.
α
s
s
h
β
.
β
a
Die Symmetrieachse teilt das gleichschenklige
Dreieck in zwei rechtwinklige Dreiecke auf.
Ein Spezialfall für ein gleichschenkliges Dreieck ist
das gleichseitige Dreieck. Es hat 3 gleich lange
Seiten, die alle mit a bezeichnet werden. Alle
Winkel messen 60°.
a
60°
60°
a
60°
a
A
Aufgabe 1: Beschriften Sie die Dreiecke korrekt. Sie sind entweder rechtwinklig oder
gleichschenklig.
Aufgabe 2: Entscheiden Sie, um welche Art von Dreieck es sich bei Ihrem Geodreieck
handelt!
Kongruente Dreiecke
Das Wort "kongruent" bedeutet deckungsgleich. Zwei geometrische Figuren heissen
kongruent, wenn man sie so übereinander legen kann, dass sie genau
übereinstimmen. Daher sind zwei Figuren auch dann noch kongruent, wenn sie
zueinander verdreht oder gespiegelt sind.
Wenn man testen will, ob zwei Dreiecke kongruent sind, muss man nicht alle Seiten
und alle Winkel der beiden Dreiecke vergleichen. Wenn ein Teil dieser Seiten und
Winkel übereinstimmt, stimmen die übrigen automatisch auch überein. Das Wort
"übereinstimmen" ist so zu verstehen:
• Zwei Seiten stimmen überein, wenn sie gleich lang sind. Sie müssen nicht
parallel sein.
• Zwei Winkel stimmen überein, wenn sie gleich gross sind. Sie müssen nicht
gleich liegen.
Zwei allgemeine Dreiecke sind in folgenden Fällen sicher kongruent:
•
•
•
•
wenn drei Seiten übereinstimmen
wenn zwei Seiten und der Zwischenwinkel übereinstimmen
wenn eine Seite und zwei Winkel übereinstimmen
wenn zwei Seiten und der an der kürzeren dieser beiden Seiten anliegende
Winkel übereinstimmen.
In all diesen Fällen lässt sich das Dreieck auch
übereinstimmenden Seiten und Winkel bekannt sind.
konstruieren,
wenn
die
Aufgabe 1: Erklären Sie, was der Unterschied zwischen Kongruenz und Ähnlichkeit ist.
Gibt es kongruente Figuren, die nicht ähnlich sind? Gibt es ähnliche Figuren, die nicht
kongruent sind? Wenn ja, zeichnen Sie zwei solche!
Aufgabe 2: Untersuchen Sie, in welchen Fällen zwei rechtwinklige Dreiecke kongruent
sind, oder anders gesagt, welche Teile (Seiten und Winkel) genügen, um ein
rechtwinkliges Dreieck zu konstruieren.
Aufgabe 3: Gleiche Aufgabe wie zuvor für gleichschenklige Dreiecke.
Aufgabe 4: Gleiche Aufgabe wie zuvor für gleichseitige Dreiecke.
Pythagoras – Mathematiker oder Sektenführer?
Pythagoras von Samos
rund 580 – 500 v. Chr.
Die Person des Pythagoras und der
nach ihm benannte religiöse Bund
der Pythagoreer sind bereits in der
Antike
durch
die
Geschichtsschreibung zur Legende
geworden. Die meisten schriftlichen
Darstellungen über Pythagoras und
seine
Anhänger
gehen
auf
Darstellungen zurück, welche im 3.
bis 4. Jahrhundert n. Chr., also rund
800 Jahre nach dem Tod von
Pythagoras, geschrieben worden
sind.
Die
bekannteste
und
ausführlichste,
aber
auch
am
stärksten parteiische und in diesem
Sinn
geschichtlich
besonders
verdächtige
Lebensbeschreibung
stammt
vom
Neupythagoreer
Jamblichos, der Ende der Antike
lebte, als durch die damalige
mystische
und
abergläubische
Anschauung
jener
Zeit
eine
Neubelebung der inzwischen unter
gegangenen religiösen Sekte der
Pythagoreer erfolgte.
Kein Wunder also, dass Jamblichos den Stammvater seiner eigenen Ansichten zum
Helden des Denkens und Forschens erheben wollte. Objektivere, aber trotzdem wenig
aufschlussreichere Berichte über Pythagoras stamme auch vom "Vater der
griechischen Geschichtsschreibung", von Herodotos, und dem bedeutenden
Philosophen Aristoteles. All diese überlieferten und wissenschaftlich ausgewerteten
Informationen sowie Rückschlüsse über die Möglichkeiten und Wahrscheinlichkeiten
der echten historischen Situation liefern etwa das folgende Bild über Pythagoras und
seine Anhängerschaft.
Es gilt als sicher, dass Pythagoras wirklich existiert hat. Das Geburtsjahr kann etwa auf
das Jahr 580 v. Chr. festgesetzt werden. Sein Vater soll Gemmenschneider auf der Insel
Samos gewesen sein, die zu dieser Zeit vom Tyrannen Polykrates beherrscht wurde.
Derselbe Tyrann wurde viel später vom deutschen Schriftsteller Friedrich Schiller in
seinem Gedicht "Der Ring des Polykrates" als ein vom Glück begünstigter Herrscher
idealisiert. Pythagoras verliess die Insel Samos wie viele andere wahrscheinlich aus
Furcht vor der drohenden Eroberung durch die aggressiven Perser. Zuerst soll er sich
nach Milet begeben haben, wo Thales seine mathematische Begabung erkannte und
ihm von den in Phönizien und Ägypten vorhandenen Wissensschätzen erzählte. In
Phönizien (heutige Küstenregion von Syrien) und Ägypten wurde Pythagoras während
eines lang dauernden Aufenthaltes mit den Mysterien verschiedenster religiöser Kulte
bekannt gemacht und lernte dort wahrscheinlich auch die überlieferte und
hochentwickelte Mathematik und Astronomie der Babylonier und Ägypter kennen.
Nach einem weiteren zwölfjährigen Aufenthalt in Babylon erreichte Pythagoras über
viele Zwischenstationen schliesslich die von Griechen bewohnte Stadt Croton in
Süditalien und gründete dort eine religiöse Sekte, die im Verlaufe der Zeit zu
beträchtlicher politischer Macht gelangte. Die Sekte der Pythagoreer wurde
schliesslich aus Croton vertrieben und liess sich darauf in einer anderen
süditalienischen Stadt, in Metapontum, nieder. Dort verbrachte Pythagoras selbst
seine letzten Lebensjahre, bevor er rund 500 v. Chr. verstarb.
Die pythagoreische Sekte vereinte die antiken mythischen Anschauungen über die
Welt mit dem sich entwickelnden Interesse für wissenschaftliche Erklärungen. Die
Pythagoreer lehrten und praktizierten eine Lebensweise, die sich auf den Glauben von
der Gefangenheit der Seele im Körper stützte. Durch den Tod werde die Seele
schliesslich befreit und in einer höheren oder niedrigeren Daseinsform, entsprechend
dem Grad der erreichten Tugend, wieder geboren. Als höchstes Ziel des Menschen
betrachteten sie die Läuterung der Seele durch die Pflege intellektueller Tugenden,
durch die Enthaltung von Sinnesfreuden und die Ausübung verschiedener religiöser
Riten. Die Pythagoreer lehrten, die Bewegung der Planeten erzeuge eine Art
"Sphärenmusik". Sie entwickelten auch eine "Musiktherapie", um die Menschheit in die
Sphärenharmonie des Himmels einzustimmen. Die Pythagoreer identifizierten die
Wissenschaft mit der Mathematik. Die Zahlen seien nicht nur das Prinzip des
Mathematischen, sondern auch des Seienden.
Von Details abgesehen, erscheint diese Schilderung des Lebens von Pythagoras
plausibel. Zumindest gibt sie auch den Hinweis, dass die damalige griechische
Wissenschaft in starkem Masse an die überlieferte babylonische und ägyptische
Wissenschaft anknüpfte. Dies gilt in besonderem Masse für die Mathematik. So ist mit
Sicherheit der nach Pythagoras benannte Satz am rechtwinkligen Dreieck schon in der
babylonischen Mathematik bekannt gewesen. Erhalten gebliebene Aufzeichnungen auf
Kelischrifttafeln zeugen davon. Wann der Lehrsatz allgemein formuliert und bewiesen
wurde, kann man heute nicht mehr genau feststellen. Die Legende schreibt
Pythagoras selbst diese Entdeckung zu. Wahr ist vermutlich, dass Pythagoras
zumindest einen Beweis für den nach ihm benannten Satz gefunden hat. Das
überrascht allerdings nicht weiter, denn heute sind über 400 verschiedene Beweise für
die Gültigkeit des Satzes von Pythagoras bekannt!
Aufgaben:
1. Suchen Sie in einem historischen Atlas (Mediothek!) die Aufenthaltsorte von
Pythagoras und stellen Sie auf der beigelegten Karte den Weg dar, den Pythagoras
in seinem Leben (vermutlich) zurückgelegt hat.
2. Suchen Sie im Internet nach weiteren Informationen über Pythagoras und sein
mathematisches und religiöses Wirken.
3. Sehen Sie Gemeinsamkeiten zwischen der pythagoreischen Sekte und heutigen
Religionen?
Pythagoras, die Wahrheit, und die Ochsen
Adelbert von Chamisso (1781 − 1838) hat den Satz von Pythagoras zur Grundlage
eines sehr ironischen Gedichts gemacht:
Vom Pythagoräischen Lehrsatz
Die Wahrheit, sie besteht in Ewigkeit,
Wenn erst die blöde Welt ihr Licht erkannt;
Der Lehrsatz nach Pythagoras benannt
Gilt heute, wie er galt in seiner Zeit.
Ein Opfer hat Pythagoras geweiht
Den Göttern, die den Lichtstrahl ihm gesandt;
Es taten kund, geschlachtet und verbrannt,
Einhundert Ochsen seine Dankbarkeit.
Die Ochsen seit dem Tage, wenn sie wittern,
Dass eine neue Wahrheit sich enthülle,
Erheben ein unmenschliches Gebrülle;
Pythagoras erfüllt sie mit Entsetzen;
Und machtlos sich dem Licht zu widersetzen
Verschließen sie die Augen und erzittern.
Fragen:
-
Was unterscheidet die Ochsen zur Zeit von Pythagoras von den Ochsen von heute?
Geschichtlich gab es immer wieder neue Wahrheiten, die ein "unmenschliches
Gebrülle" hervorgerufen haben. Welche Beispiele kennen Sie?
Der Satz von Pythagoras und sein Beweis
Der Satz von Pythagoras lautet in Worten:
In einem rechtwinkligen Dreieck haben die Quadrate über den Katheten zusammen den gleichen
Flächeninhalt wie das Quadrat über der Hypotenuse.
Statt "Quadrat über der Kathete" und "Quadrat über der
Hypotenuse" sagt man oft auch "Kathetenquadrat" und
"Hypotenusenquadrat". In der Zeichnung rechts sind a2
und
b2
die
Kathetenquadrate,
c2
ist
das
Hypotenusen-quadrat. Der Satz von Pythagoras lautet mit
diesen Bezeichnungen
b
2
a
b
2
a
c
a2 + b2 = c2
c
2
Der einfachste Beweis für den Satz von Pythagoras ist aus etwa 2000 Jahre alten chinesischen
Quellen überliefert. Vermutlich hat unabhängig davon auch Pythagoras diesen Beweis selbst
entdeckt.
a
b
b
b
a
c
c
a2
a
a
b
b b2
a
2
c
a
c
c
b
a
c2
b
b
=
b2
a
+ a2
Das grosse Quadrat mit Seitenlänge (a+b) enthält links und rechts viermal das
rechtwinklige Dreieck mit den Seiten a, b und c. Die restliche Fläche wird links durch c 2
ausgefüllt, rechts durch a2 und b2.
Aufgabe 1: Lernen Sie den Beweis auswendig. Sie sollen in der Lage sein, ihn mit
Geodreieck, Bleistift und Papier selbst durchzuführen und vorzuzeigen.
Aufgabe 2: Studieren Sie die Zeichnungen auf der Rückseite und erklären Sie, wie
man daraus den Satz des Pythagoras ableiten kann.
B e w e is v o n N A IR IZ I
K U K M A LD H A
S C H A U H IN
c2
2
a
b2
Der Höhensatz
Der Höhensatz besagt:
Im rechtwinkligen Dreieck ist das Quadrat der Höhe gleich gross wie das Rechteck aus
den Hypotenusenabschnitten. Es gilt also
h2 = pq
h
h2
.
a
b
h
.
q
p
q
pq
q
Mit Hypotenusenabschnitten sind die Teile der Hypotenuse gemeint, die links und
rechts von der Höhe liegen. Sie werden mit q und p bezeichnet.
Die Richtigkeit des Satzes kann man aus den folgenden beiden Figuren ablesen:
b
q
h
h
a
h
a
h2
h
q
p
b
pq
q
h
p
p
q
h
Die beiden grossen rechtwinkligen Dreiecke haben die Katheten (h+q) und (h+p),
sowie die Hypotenuse (a+b). In beide werden das rechtwinklige Dreieck mit den Seiten
b, h und q sowie das rechtwinklige Dreieck mit den Seiten a, h und p eingefüllt. Übrig
bleibt links die Fläche h2, rechts die Fläche pq.
Aufgabe: Zeigen Sie, dass das Dreieck mit den Seiten b, h und q ähnlich ist zum
Dreieck mit den Seiten a, h und p. Verwenden Sie dazu das oberste Bild.
Der Kathetensatz (Satz von Euklid)
Im Gegensatz zum Satz von Pythagoras ist es ziemlich sicher, dass der Satz von Euklid
wirklich von Euklid entdeckt und bewiesen wurde.
Der Kathetensatz besagt:
In einem rechtwinkligen Dreieck ist ein Kathetenquadrat so gross wie das Rechteck
aus der Hypotenuse und dem anliegenden Hypotenusenabschnitt. Also:
a2 = pc
a
a2
b
2
a
b
h
q
p
              
c
c
qc
c
pc
c
Hypotenusenabschnitte nennt man die Teile der Hypotenuse, die links und rechts von
der Höhe liegen.
Der Satz gilt natürlich nicht nur für den rechten Hypotenusenabschnitt und die rechte
Kathete, sondern auch für den linken Hypotenusenabschnitt und die linke Kathete.
Daher ist auch
b2 = qc
Um zu zeigen, dass der Satz richtig ist, kann man benutzen, dass das Dreieck aus den
Seiten p, h und a zum Dreieck aus den Seiten a, b und c ähnlich ist. Wegen dieser
Ähnlichkeit ist
a
c
=
p
a
Indem man beide Seiten dieser Gleichung mit ap multipliziert, erhält man a 2 = pc.
Aufgabe 1: Kennzeichnen Sie die genannten Dreiecke mit verschiedenen Farben und
erklären Sie, warum sie ähnlich sind.
Aufgabe 2: Wiederholen Sie den Beweis mit dem linken Teildreieck und zeigen Sie
damit, dass b2 = qc ist.
Wie sind Sinus, Cosinus und Tangens definiert, und was kann man
damit berechnen?
Um ein rechtwinkliges Dreieck zu konstruieren, braucht man nicht die Grössen aller
Winkel und die Längen aller Seiten zu kennen. Es genügt
• wenn man die Längen beider Katheten kennt
• wenn man die Länge eine Kathete und die Länge der Hypotenuse kennt
• wenn man die Länge der Hypotenuse und die Grösse eines Winkels (zusätzlich zum
rechten Winkel) kennt.
• wenn man die Länge einer Kathete und die Grösse eines Winkels (zusätzlich zum
rechten Winkel) kennt.
Der Satz des Pythagoras erlaubt es auch, die Länge einer Seite zu berechnen, wenn
die Längen der anderen beiden Seiten bekannt sind. Was Sie heute neu lernen, ist, wie
man die Längen der fehlenden Seiten berechnen kann, wenn man die Länge einer
Seite und die Grösse eines Winkels (zusätzlich zum rechten Winkel) kennt. Man benutzt
dazu Sinus, Cosinus und Tangens.
Im folgenden sind alle möglichen Fälle aufgelistet. Damit Sie sie nachrechnen können,
sind jeweils auch Zahlen angegeben, die natürlich nur als Beispiele zu verstehen sind.
1. Fall: Sie kennen die Hypotenuse c = 5 und einen Winkel (z.B. α = 40°).
Gesucht sind die Längen der Katheten a und b.
Lösung: Der Winkel α bestimmt, wie gross die
Verhältnisse a : c und b : c sind. Theoretisch muss
es daher möglich sein, a : c und b : c zu
berechnen, wenn man nur α kennt. Nur wie? a : c
ist nicht α selbst, es ist auch nicht das Quadrat
von α, es ist auch nicht die Wurzel von α, sondern
etwas anderes: Man nennt es den Sinus von α
und schreibt dafür sin α. b : c nennt man den
Cosinus von α und schreibt dafür cos α.
α
c
b
a
Gegenkathe
te
Hypotenuse
Ankathete
Cosinus von α = cos α = b : c =
Hypotenuse
Sinus von α = sin α = a : c =
Warnung: Sagen Sie für sin α niemals "Sinus mal α". sin α ist der Sinus von α.
Den Sinus von α und den Cosinus von α kann man mit dem Taschenrechner
berechnen, und zwar gleich, wie die das Quadrat oder die Wurzel einer Zahl.
Berechnung von sin 40°:
4 0
sin ⇒ Ergebnis: 0.6427876097
Berechnung von cos 40°:
4 0
cos ⇒ Ergebnis: 0.7660444431
Wie lassen sich nun a und b berechnen? Zunächst zu a: Sie lösen die Gleichung sin α =
a : c nach a auf:
a
sinα =
|⋅c
c
c ⋅ sinα = a
Wenn Sie für c = 5 und für α = 40° nehmen, sollten Sie 3.213938048 erhalten. Es ist
allerdings unsinnig, so viele Stellen anzugeben. Im Normalfall genügen zwei Stellen
nach dem Komma, also a = 3.21.
Aufgabe: Berechnen Sie nun auch b. Sie sollten 3.83 erhalten!
2. Fall: Sie kennen den Winkel α = 70° und die Gegenkathete a = 4.5.
Gesucht sind die Hypotenuse und die Ankathete b.
α
Lösung: Um die Hypotenuse c auszurechnen,
gehen Sie zunächst vor wie im 1. Fall: Sie
benutzen
sinα =
c
a
c
b
a
Dieses Mal müssen Sie die Gleichung aber nicht nach a, sondern nach c auflösen:
a
|⋅c
c
c ⋅ sinα = a | : sinα
a
c=
sinα
sinα =
a
können Sie so in den
sinα
4 .
5 ÷
7
0
sin
Es ist also ein zusätzlicher Schritt erforderlich.
Taschenrechner eintippen (mit a = 4.5, α = 70°):
=
Das Ergebnis sollte 4.79 (gerundet auf 2 Stellen nach dem Komma) sein!
Jetzt, wo Sie c kennen, ist auch b einfach zu berechnen, nämlich mit dem Satz von
Pythagoras: Aus a2 + b2 = c2 folgt b2 = c2 – a2 und daraus b = c2 − a2 . Allerdings wäre
es eleganter, wenn man b ohne den Umweg über c ausrechnen könnte. Nur wie? Mit
a
b
sinα =
und cosα = lässt sich der Umweg über c nicht vermeiden, weil in beiden
c
c
Gleichungen c vorkommt. Wir brauchen nicht das Verhältnis a : c und auch nicht das
Verhältnis b : c, sondern das Verhältnis a : b. Auch dieses Verhältnis hängt nur vom
Winkel α ab und hat einen Namen: Man nennt es den Tangens von α.
Tangens von α = tan α = a : b =
Gegenkathe
te
Ankathete
Wenn Sie diese Gleichung nach b auflösen, erhalten Sie die Ankathete, ohne den
Umweg über c zu machen:
a
| ⋅b
b
b ⋅ tanα = a | : tanα
tanα =
b=
Sehen Sie oben nach, wie Sie
a
tanα
a
in den Taschenrechner eintippen. Auf die gleiche
sinα
a
eintippen. Sie sollten (mit a = 4.5, α = 70°) den Wert 1.64
tanα
(gerundet auf zwei Stellen nach dem Komma) erhalten.
Art können Sie
Aufgaben
12
10
4.31
,
,
, 5 ⋅ sin30°, 3 ⋅ cos30°, 6 ⋅ tan60°
tan15° cos 60° sin1°
Ergebnisse: 44.78, 20, 246.96, 2.5, 1.5, 4.24
1. Berechnen Sie
a
für a = 3 und α = 60°, b ⋅ tan β für b = 0.3, β = 45°
sinα
Ergebnisse: 3.46, 0.3
2. Berechnen Sie
3. Fall: Sie kennen den Winkel α = 55° und die Ankathete b = 10. Gesucht
sind die Gegenkathete a und die Hypotenuse c.
Lösung: Mit dem Tangens erhalten Sie eine
Verknüpfung zwischen den gegebenen Grössen
(Ankathete b und Winkel α) und der Gegenkathete
a:
tanα =
a
b
α
c
b
a
Um a zu berechnen, lösen Sie die Gleichung nach a auf:
a
| ⋅b
b
b ⋅ tanα = a
tanα =
Mit b = 10 und α = 55° erhalten Sie a = 14.28.
Eine Verknüpfung zwischen den gegebenen Grössen (Ankathete b und Winkel α) und
der Hypotenuse c liefert der Cosinus:
b
cosα =
c
Aufgabe: Lösen Sie die Gleichung nach c auf und berechnen Sie c. Sie sollten 17.43
erhalten.
Aufgabe: Lösen Sie das beigelegte Rätsel!
Wann immer ein Winkel und eine Seite eines rechtwinkligen Dreiecks gegeben sind,
liegt einer der drei Fälle vor, die Sie jetzt gelesen haben. Sie können also stets die
Längen alle fehlenden Seiten berechnen. Nun lernen Sie noch, wie Sie einen Winkel
berechnen, wenn Sie zwei Seiten eines rechtwinkligen Dreiecks kennen. Auch hier gibt
es wieder drei Fälle, die wir die Fälle 4 bis 6 nennen.
Fall 4: Sie kennen die Gegenkathete a = 12 und die Hypotenuse c = 19.
Gesucht ist der Winkel α.
a
. Sie
c
kennen a und c, können also die rechte Seite der
Gleichung berechnen:
Lösung: Wie Sie schon wissen, ist sinα =
sinα =
a 12
=
= 0.6315789474
...
c 19
α
c
b
a
Wie kommt man auf α, wenn man nur den Sinus von α kennt? Überlegen Sie sich dazu,
wie Sie auf x kommen, wenn Sie nur das Quadrat von x kennen: Sie führen eine
Operation aus, die das Quadrieren gerade wieder rückgängig macht. Diese Operation
ist das Wurzelziehen. Wenn Sie z. B. wissen, dass x 2 = 81 ist, bekommen Sie x, indem
Sie die Wurzel von 81 berechnen: x = 81 = 9. Das können Sie so schreiben:
x2 = 81 ⇒ x =
81
Die Operation, die den Sinus rückgängig macht, hat den Namen Arcussinus. Man
schreibt sie kurz als arc sin. Ganz analog zur Methode, die das Quadrieren rückgängig
macht, wird der Sinus also so rückgängig gemacht:
sinα = 0.63157894
74...⇒ α = arc sin0.63157894
74...
Um nicht die langen Dezimalbrüche zu haben, können Sie auch schreiben:
12
12
⇒ α = arc sin
19
19
Auf dem Taschenrechner wird der Arcussinus mit sin -1 bezeichnet. sin-1 steht als zweite
12
Tastenbelegung über der sin-Taste. Um den Arcussinus von
zu berechnen, tippen
19
Sie
1 2 ÷ 1 9 = 2nd sin
sinα =
Sie sollten α = 39.17° erhalten.
Hinweis: Auf einigen Taschenrechnern gibt es keine 2nd-Taste, statt dessen aber
eine Shift- oder eine INV-Taste.
Aufgaben:
1. Berechnen Sie α, wenn sin α = 0.5. Ergebnis: α = 30°.
2. Berechnen sie α, wenn sin α =
13
.
15
Ergebnis: α = 60.07°.
Fall 5: Sie kennen die Ankathete b = 16 und die Hypotenuse c = 18. Gesucht
ist der Winkel α.
Lösung: Die Beziehung, die beide gegebenen und die
gesuchte Grösse enthält, ist
cosα =
α
c
b
b
c
a
Ganz analog zum Arcussinus nennt man die Operation, die den Cosinus rückgängig
macht, Arcuscosinus, kurz arc cos. Auf dem Taschenrechner wird sie cos -1 genannt. Sie
berechnen α daher so:
b
b
16
cosα = ⇒ α = arc cos = arc cos
c
c
18
und auf dem Taschenrechner
1 6 ÷ 1 8 = 2nd cos
Das Ergebnis ist α = 27.27°.
Fall 6: Sie kennen die Ankathete b = 3 und die Gegenkathete a = 2. Gesucht
ist der Winkel α.
Lösung: Dieser Fall ist ganz analog zu den Fällen 5 und 6. Der Unterschied liegt darin,
dass Sie mit der Gleichung
a
tanα =
b
starten und die Operation Arcustangens (kurz arc tan, auf dem Taschenrechner tan -1)
verwenden, um den Tangens rückgängig zu machen. Das Resultat ist α = 33.69°.
Zusammenfassung
Berechnungsaufgaben am rechtwinkligen Dreieck können so gelöst werden:
1. Wählen Sie die Beziehung, die die gegebenen Grössen mit der gesuchten Grösse
verknüpft. Dabei stehen folgende Beziehungen zur Auswahl:
Gegenkathe
te bezgl.ϕ
Hypothenus
e
Ankathete
bezgl.ϕ
cosϕ =
Hypothenus
e
Gegenkathe
te bezgl.ϕ
tanϕ =
Ankathete
bezgl.ϕ
sinϕ =
(Gegenkathete)2 + (Ankathete)2 =
(Hypotenuse)2
2. Schreiben Sie diese Beziehung mit den Buchstaben auf, mit denen die Seiten und
Winkel in der Aufgabe bezeichnet werden.
3. Lösen Sie die Beziehung algebraisch nach der gesuchten Grösse auf.
4. Setzen Sie Zahlen für die Buchstaben ein und berechnen Sie die gesuchte Grösse
mit dem Taschenrechner.
Aufgabe
Von einem rechtwinkligen Dreieck sind einige der Grössen a, b, c, α und β gegeben, die
übrigen sind zu berechnen. Um Ihnen den Einstieg zu erleichtern, wird a) vorgelöst.
a)
b)
c)
d)
e)
f)
g)
a
a
b
b
b
a
a
= 4, β = 20°
= 5, α = 30°
= 4, c = 9
= 8, α = 12°
= 11, β = 25°
= 8, c = 19
= 3, b = 1
α
c
b
β
a
Ergebnisse:
a) Wir berechnen zuerst die Hypotenuse c. Bezüglich β ist a die Ankathete. Die
geeignete Beziehung ist daher
cosϕ =
Ankathete
bezgl.ϕ
Hypothenus
e
Mit den in der Aufgabe benutzten Buchstaben:
a
cosβ =
c
Nach c auflösen:
Einsetzen:
cosβ =
a
a
⇒ c ⋅ cosβ = a ⇒ c =
c
cosβ
c=
4
= 4.26.
cos20°
Nun berechnen wir die Gegenkathete b. Mit den in der Aufgabe benutzten
Buchstaben gilt
b
tanβ =
a
b
tanβ = ⇒ a ⋅ tanβ = b
Nach b auflösen:
a
Einsetzen:
b = 4 ⋅ tan20° = 1.46.
Es fehlt noch der Winkel α: Weil in jedem rechtwinkligen Dreieck α + β = 90° ist,
findet man α = 90° – β = 90° – 20° = 70°.
a
a
= 10.00, b =
= 8.66, β = 90° − α = 60°
b) c =
sinα
tanα
b
c) a = c2 − b2 = 8.06, α = arc cos = 63.61, β = 90° − α = 26.39°
c
d) c = 8.18, a =1.70, β = 78°
e) c = 26.03, a = 23.59, α = 65°
f) b =17.23, α = 24.90, β = 65.10°
g) c = 3.16, α = 71.57, β =18.43°
RÄTSEL
Die Buchstaben hinter den richtigen Beziehungen ergeben das Lösungswort.
1.
c
b
b
cos β =
c
a
tan α =
b
v
tan θ =
w
u
cos ϕ =
w
v
cos θ =
u
q
sin ρ =
r
sin α =
β
c
a
α
b
w
2.
ϕ
v
u
θ
q
3.
ω
p
sin ρ =
r
ρ
i
h
4.
σ
ϑ
j
ξ
6.
p
7.
w
ε
γ
u
s
d
δ
f
ζ
8.
Σ
f
φ
g
s
Γ
11.
n
d
τ
ϒ
r
f
12. ψ
ν
z
H
d
L
13.
N
r
a
S
ς
d
κ
G
14.
I
d
ι
T
s
U
η
15.
E
λ
N
2
3
4
5
6
7
r
o
f
G
r
F
χ
o
1
Lösungswort:
I
Ξ
c
Ü
j
i
i
j
o
R
cos ϑ =
l
10.
E
S
d
α
A
r
p
a
m
m
cos µ =
r
m
sin µ =
a
p
tan γ =
w
p
cos ε =
w
p
sin ε =
w
d
sin δ =
s
f
cos ζ =
d
s
cos δ =
f
g
cos Σ =
f
g
sin φ =
o
m
h
F
8
9
0
11
12
13
l
h
d
tan Ω =
l
l
cos α =
d
s
cos Γ =
c
c
sin Ξ =
s
s
sin Γ =
o
n
sin ϒ =
d
n
tan ϒ =
r
n
cos τ =
r
z
tan ν =
d
f
cos ψ =
z
z
cos ν =
f
r
sin κ =
d
a
sin ς =
r
a
tan κ =
d
d
cos ι =
r
r
cos η =
s
s
sin ι =
r
o
tan λ =
f
r
cos χ =
f
o
sin λ =
f
o
tan χ =
f
r
sin χ =
o
sin Ω =
Ω
I
tan ξ =
r
9.
D
tan ω =
sin σ =
a µ
5.
r
q
R
14
15
S
N
A
W
A
L
A
L
N
F
H
E
A
N
R
Ä
N
P
R
Z
E
G
D
Pythagoreische Halbkreise und andere Figuren
F
Nach
Pythagoras
hat
die
Summe
der
Kathetenquadrate den gleichen Flächeninhalt wie das
Hypotenusenquadrat. Der Satz stimmt aber auch
dann noch, wenn man die Quadrate durch andere
Figuren ersetzt, z.B. durch Halbkreise. So ist in der
nebenstehenden Figur Fa + Fb = Fc. Die
Katheten-halbkreise haben zusammen den gleichen
Flächeninhalt wie der Hypotenusenhalbkreis.
b
b
a
F
a
c
F
c
Um zu verstehen, warum das so ist, zeichnen wir die
Quadrate, die beim "gewöhnlichen" Satz von
Pythagoras vorkommen, neben diese Halbkreise:
b
2
a
b
Fb
c
b
2
a
2
c
Fa
2
a
Fc
2
c
2
Die drei Figuren, die dabei entstehen, sind zueinander ähnlich. Daher ist
Fa Fb Fc
=
=
a2 b2 c2
Wenn
wir
dieses
Verhältnis
mit
k
bezeichnen,
bedeutet
das,
dass
Fa
F
F
π
.. ). Daraus
= k, b2 = k und c2 = k ist (man kann ausrechnen, dass k = = 0.392699
2
8
a
b
c
folgt nun, dass Fa = k·a2, Fb = k·b2 und Fc = k·c2 ist. Somit ist
Fa + Fb = k·a2 + k·b2 = k·(a2 + b2) = k·c2 = Fc.
Aufgabe: Denken Sie sich weitere Figuren aus, die man an Stelle der Quadrate an die
Seiten eines rechtwinkligen Dreiecks legen könnte. Ein Beispiel sehen sie hier:
Pythagoras in drei Dimensionen
Raumdiagonale eines Quaders
Mit dem Satz von Pythagoras lässt sich die Länge der Diagonale in einem Rechteck
leicht bestimmen:
d
b
.
a
Da die Diagonale das Rechteck in zwei rechtwinklige Dreiecke zerteilt, gilt d 2 = a2 +
b2.
c
b
D
.
d
.
a
In einem Quader nennt man die Linie, die von einer Ecke zur quer gegenüberliegenden
Ecke führt, Raumdiagonale. In der Zeichnung ist sie mit D beschriftet. Da die Seite c
senkrecht steht und die Flächendiagonale d waagrecht liegt, ist das Dreieck mit den
Seiten c, d und D rechtwinklig. D ist die Hypotenuse. Darum ist D 2 = d2 + c2.
d ist die Diagonale in einem Rechteck. Daher wissen wir bereits, dass d 2 = a2 + b2 ist.
Wenn man beide Gleichungen kombiniert, erhält man daraus
D2 = a2 + b2 + c2
Weil diese Gleichung sehr ähnlich aussieht wie der Satz des Pythagoras selbst, nennt
man sie auch den dreidimensionalen Satz des Pythagoras.
Aufgabe 1: Berechnen Sie die Länge der Raumdiagonale eines Quaders mit a = 3, b
= 4, c = 12
Aufgabe 2: Die Raumdiagonale eines 4 m breiten und 5 m langen Quaders misst 21
m. Wie hoch ist der Quader?
Aufgabe 3: Ein Würfel hat die Kantenlänge 5. Wie lang ist seine Raumdiagonale?
Aufgabe 4: Welche Kantenlänge hat ein Würfel, dessen Raumdiagonale 81 cm lang
ist?
Kantenlänge einer Pyramide
Die
nebenstehende
Pyramide
hat
eine
quadratische Grundfläche mit Seitenlänge a und
eine Höhe h. Wie gross ist die Kantenlänge s?
Das fett gezeichnete Dreieck in der Grundfläche
ist rechtwinklig. Beide Katheten haben je die
Seitenlänge
a
2
. Die Hypotenuse ist halb so lang
h
s
a
wie die Diagonale des Quadrats, hat also die
Länge
man
d
2
d
2
. Mit dem Satz von Pythagoras kann
ausrechnen, wenn man a kennt. Es gilt
2
2
2
2
d
2
a
2
.
.
a
2
a
2
a
a
a2
 d
 a
 a
+
=
  =   +  =
4
4
2
 2
 2
 2
Das Dreieck mit den Seiten h,
2
d
2
und s ist ebenfalls rechtwinklig. s ist die Hypotenuse.
2
d
d
2
Daher ist s2 = 
 
 + h . Da wir 
 
 bereits ausgerechnet haben, erhalten wir
2
2
 
 
s2 =
a2
+ h2
2
Aufgabe 5: Berechnen Sie die Seitenlänge einer Pyramide mit der Höhe h = 63 und
der Kantenlänge s = 100.
Aufgabe 6: Angenommen, die Pyramide habe statt der quadratischen eine
rechteckige Grundfläche mit den Seitenlängen a und b. Wie lässt sich die Kantenlänge
dann aus a, b und h berechnen?
Gleichschenklige Dreiecke und Pythagoras
α
Die Höhe teilt ein gleichschenkliges Dreieck in zwei
kongruente rechtwinklige Dreiecke. Für diese Teildreiecke
gilt der Satz von Pythagoras natürlich auch. Allerdings
a
2
sind die Katheten jetzt h und
s
(die Hälfte der Seite a).
Die Hypotenuse ist s. Daher lautet der Satz von
Pythagoras jetzt
s
h
a
2
β
a
2
β
a
2
 a
  + h2 = s2
 2
Ein Spezialfall des gleichschenkligen Dreiecks ist das
gleichseitige Dreieck. Hier sind Schenkel und Basis gleich
lang. Im halbierten gleichseitigen Dreieck sind die
Katheten h und
a
2
a
a
2
, die Hypotenuse ist a. Also ist
a
h
a
2
a
2
 a
  + h2 = a2
 2
Im gleichseitigen Dreieck kann man die Höhe ausrechnen, wenn man die Länge einer
 a
 2
2
Seite kennt. Dazu löst man die Gleichung   + h2 = a2 nach h auf:
2
 a
  + h2 = a2
 2
 a
|-  
 2
2
2
a2
4a2 − a2 3a2
3
 a
h2 = a2 −   = a2 −
=
=
= a2 |
2
4
4
4
4
 
h=
3 2
a =
4
3
4
a2 =
(....)
3
a
2
Bei der letzten Umformung wurde benutzt, dass
ab =
a b
und
a
=
b
a
b
ist.
Aufgabe: Die Fläche eines Dreiecks ist Grundlinie × Höhe ÷ 2. Welche Fläche hat
dann ein gleichseitiges Dreieck mit der Grundlinie a = 5?
Konstruktionsaufgaben mit rechtwinkligen und gleichschenkligen
Dreiecken
Neben den Standardkonstruktionen lernen Sie hier, wie man mit Höhen- und
Kathetensatz zu einem gegebenen Quadrat flächengleiche Rechtecke konstruiert und
umgekehrt. Einige dieser Aufgaben benötigen ausserdem die Thaleskreiskonstruktion.
Daher beginnt der Posten mit einem Theorieteil.
C2
C1
Thaleskreis
Gegeben ist eine Strecke AB mit dem Mittelpunkt M.
Zeichnet man einen Kreis, dessen Mittelpunkt
ebenfalls M ist und dessen Radius gleich MA = MB
ist, und wählt einen beliebigen Punkt C auf dem
Kreis, so hat das Dreieck ABC immer bei C einen
rechten Winkel.
M
A
B
C3
C4
Dieser Kreis heisst Thaleskreis über der Strecke AB.
C
Um zu beweisen, dass der Winkel bei C 90° beträgt,
betrachten wir zusätzlich zum Dreieck ABC die
Strecke MC. Da MA, MB und MC Kreisradien
sind, sind sie gleich lang, und daher sind die Dreiecke
AMC und MBC gleichschenklig. Der Winkel in der Ecke
C setzt sich daher aus α und β zusammen.
Da in jedem Dreieck die Winkelsumme 180° beträgt,
ist
δ = 180° – 2α und ε = 180° – 2β. Wegen δ + ε
= 180° folgt daraus, dass 180° – 2α + 180° – 2β =
180° ist. Mit wenigen Vereinfachungsschritten kann
man daraus folgern, dass
α + β = 90° sein muss.
Damit ist der Beweis erbracht.
r
A
r
r
α
β
B
β
B
M
C
α β
A
ε
δ
α
M
Mit dem Thaleskreis kann man z.B. die folgenden
Probleme lösen (weitere finden Sie in den Aufgaben):
1. Konstruieren Sie ein rechtwinkliges Dreieck aus p und q. Lösung:



p
q
2. Konstruieren Sie ein rechtwinkliges Dreieck aus c und h.
Lösung:



c
Aufgabe 1: Beide Aufgaben haben noch eine zweite Lösung. Finden Sie sie!

h
Aufgabe 2: Benutzen Sie den Kathetensatz, um das erste Problem rechnerisch zu
lösen. Konkret:
Von einem rechtwinkligen Dreieck kennt man p = 5 und q = 2, gesucht sind a und b.
(Lösung: a = 35 , b = 14 )
Quadratur eines Rechtecks
Man benutzt manchmal umgangssprachlich den Ausdruck "Quadratur des Kreises" für
eine extrem schwierige Sache. Mathematisch ist mit der Quadratur des Kreises
gemeint: Ein Quadrat konstruieren, das den gleichen Flächeninhalt wie ein
vorgegebener Kreis hat:
?
F
F
Seit der Antike haben sich berühmte Mathematiker die Köpfe an diesem Problem
zerbrochen. Heute weiss man, dass diese Aufgabe unlösbar ist.
Viel einfacher ist es, ein Rechteck zu
quadrieren, also zu einem gegebenen
Rechteck ein flächengleiches Quadrat zu
konstruieren. Dazu benutzt man z.B. den
Höhensatz:
In Schritt 2 wurde dabei ein Thaleskreis über
der Strecke AB gezeichnet. Das rechtwinklige
Dreieck ist gestrichelt dargestellt.
h



A
q
B
p
p
Das Rechteck und das Quadrat haben die
gleiche Fläche, weil nach dem Höhensatz h 2
= pq ist.

b
Das gleiche Problem kann auch mit dem
Kathetensatz gelöst werden:

Wieder wird im 2. Schritt ein Thaleskreis über
der Strecke AB gezeichnet. Das Rechteck und
das Quadrat haben die gleiche Fläche, weil
nach dem Kathetensatz b2 = cq ist.

b
A

B
q
c

Aufgaben
B
1. Konstruieren Sie ein rechtwinkliges Dreieck aus β
a) a = 3 cm, b = 4 cm
b) c = 8 cm, α = 30°
a
c) c = 7 cm, h = 3 cm
d) c = 12 cm, a = 5 cm
.
e) h = 9 cm, β = 40°
f) h = 4 cm, a = 6 cm
2. Konstruieren Sie ein gleichschenkliges Dreieck aus
a) a = 5 cm, s = 7 cm
b) a = 8 cm, h = 11 cm
c) a = 6 cm, β = 40°
d) a = 6 cm, α = 40°
e) h = 8 cm, α = 70°
f) h = 8 cm, β = 70°
g) s = 12 cm, h = 9 cm (Thaleskreis!)
h) s = 10 cm, β = 50°
.
c
h
α
b
α
s
s
h
β
.
β
a
3. Konstruieren Sie ein Quadrat, das denselben Flächeninhalt hat wie
a) ein Rechteck mit a = 8.5 cm und b = 2 cm
b) die beiden Quadrate mit Kantenlängen 4 cm und 2.5 cm zusammen
c) die Differenz der beiden Flächeninhalte von b).
4. Zeichnen Sie ein Quadrat mit der Seitenlänge 4 cm und konstruieren Sie ein
flächengleiches Rechteck mit
a) einer Seitenlänge 3 cm
b) dem Umfang 20 cm
c) dem Seitenverhältnis 9 : 4
Formelsammlung
Diese Formelsammlung ist nicht dazu da, um an der Prüfung verwendet zu werden,
sondern um sie bis zur Prüfung auswendig zu lernen!
Rechtwinkliges Dreieck:
1
2
Flächeninhalt: F =
ab =
2
1
2
hc
2
.
2
Satz von Pythagoras: a + b = c
a
b
h
Höhensatz: h2 = p q
Kathetensatz (Satz von Euklid): a2 = c p, b2 = c q
.
p
q
c
Gleichschenkliges Dreieck:
Flächeninhalt: F =
1
2
s
s
ah
h
.
2
Satz von Pythagoras: s2 =  a  + h2
2
 
a
Gleichseitiges Dreick:
Höhe: h =
3
2
a
a
Flächeninhalt: F =
3
4
a
h
.
a2
a
Trigonometrische Funktionen:
Gegenkathe
te bzgl.ϕ
Hypothenus
e
Ankathete
bzgl.ϕ
cosϕ =
Hypothenus
e
Gegenkathe
te bzgl.ϕ
tanϕ =
Ankathete
bzgl.ϕ
sinϕ =
Aufgabe: Lernen Sie diese Formeln auswendig!
Hypotenuse
.
ϕ


Gegenkathet
e
Sinus, Cosinus und Tangens bei gleichschenkligen Dreiecken
Gleichschenklige
Dreiecke
sind
normalerweise nicht rechtwinklig, man kann
sie aber entlang ihrer Symmetrieachse (die
gleichzeitig die Höhe ist) in zwei kongruente
rechtwinklige
Dreiecke
aufteilen. Dabei
werden die Basis und der gegenüberliegende
Winkel halbiert.
αα
22
h
a
2
.
β
Wir schreiben zunächst alle Beziehungen mit
dem Winkel β auf. Bezüglich β ist h die
Gegenkathete,
s
s
Durch diese Halbierungen entstehen beim
Aufschreiben
der
Beziehungen
einige
Doppel-brüche.
Ausserdem
muss
beim
Auflösen einer Beziehung nach dem Winkel α
vorsichtig vorgegangen werden.
β
die Ankathete und s die
Hypotenuse. Daher gilt:
sinβ =
a
2
h
h
h
⇔ s ⋅ sinβ = h ⇔ s =
⇔ β = arc sin
s
sinβ
s
a
a
a
⇔ 2s ⋅ cosβ = a ⇔ s =
⇔ β = arc cos
s
2s
2 ⋅ cosβ
2s
h
2h
a
2h
2h
tanβ =
=
⇔ ⋅ tanβ = h ⇔ a =
⇔ β = arc tan
a
a
2
tanβ
a
cosβ =
=
2
Angenommen, a = 4 und β = 20° sind gegeben, gesucht ist s. Dann müssen Sie beim
Eintippen der Formel s =
a
darauf achten, dass Sie wirklich a ÷ (2 × cos β) und
2 ⋅ cosβ
nicht a ÷ 2 × cos β eingeben. Die richtige Tastenfolge ist (im Fall von a = 4 und β =
20°) daher
4 ÷ ( 2 × 2 0 cos ) =
Stellen Sie sicher, dass Sie als Ergebnis 2.128355545 und nicht 1.879385242
bekommen. Das zweite Ergebnis bekommen Sie, wenn Sie die Klammern vergessen.
Wir schreiben nun die Beziehungen mit dem Winkel
Ankathete,
a
2
α
2
auf. Bezüglich
die Gegenkathete und s die Hypotenuse. Somit ist
α
sin
2
=
a
2
=
s
a
a
a
α
⇔ 2s ⋅ sin = a ⇔ s =
⇔ α = 2 ⋅ arc sin
α
2
2s
2s
2 ⋅ sin
2
α
2
cos =
h
h
h
α
⇔ s ⋅ cos = h ⇔ s =
⇔ α = 2 ⋅ arc cos
α
2
s
s
cos
2
α
2
tan =
a
2
h
=
a
a
a
α
⇔ 2h ⋅ tan = a ⇔ h =
⇔ α = 2 ⋅ arc tan
α
2
2h
2h
2 ⋅ tan
2
α
2
ist h die
Aufgabe 1: Rechnen Sie die Umformungen nach. Ist alles richtig?
Aufgabe 2: In einem gleichschenkligen Dreieck
sind zwei der Grössen a, s, α, β und h gegeben.
α
Gesucht sind die übrigen. Als Einstieg ist die erste
Teilaufgabe vorgelöst.
a)
b)
c)
d)
e)
s
s
s = 58.6, β = 62.7°
a = 125, β = 36.3°
s = 51.4, h = 43.8
h = 9.65, α = 106.7
a = 86.4, h = 93.9
h
β
.
β
a
Lösungen:
a) Wir berechnen zuerst h. Bezüglich β ist h die Gegenkathete, s ist die Hypotenuse.
Also gilt
h
sinβ =
s
Aufgelöst nach h:
h = s · sin β
Zahlen eingesetzt:
h = 58.6 · sin 62.7° = 52.07
Nun berechnen wir a. Bezüglich β ist
a
2
die Ankathete. Daher ist
cosβ =
Aufgelöst nach a:
Zahlen eingesetzt:
Nun fehlt noch α. Da
b) s =
a
2
=
a
2s
s
a = 2 s · cos β
a = 2 · 58.6 · cos 62.7° = 53.75
α
+
2
β = 90°, ist
α
2
= 90° - β und α = 180° - 2β = 54.6°.
a
a
= 77.55, h = ⋅ tanβ = 45.91, α = 180° - 2β = 107.4°
2 ⋅ cosβ
2
h
c) a = 2 ⋅ s 2 − h2 = 53.80, β = arc sin = 58.45, α = 180° - 2β = 63.11°
s
d) a = 25.94, s = 16.17, β = 36.65
e) s = 103.36, β = 65.29, α = 49.41
Die Höhe des Schulhauses messen
1. Messen Sie mit dem Messband selbst gewählte Distanzen d 1 und d2 ab, und messen
Sie von diesen Standpunkten aus mit dem Peilgerät die Winkel α1 und α2 ab. Sie
können daraus die Höhen h1 und h2 entweder dadurch bestimmen, dass Sie die
Dreiecke in verkleinertem Massstab konstruieren und dann die entsprechenden
Seiten abmessen, oder indem Sie trigonometrische Funktionen benutzen.
h2
α2
d2
h1
α1
d1
2. Vergleichen Sie die so erhaltenen Höhen mit denjenigen, die Sie erhalten, wenn Sie
die Treppenstufen zählen und die Höhe einer Stufe abmessen.
3. Überlegen Sie sich weitere Möglichkeiten zur Bestimmung einer Gebäudehöhe.
Steigung und Steigungswinkel
Auf Strassenschildern gibt man die Steigung
in Prozent an. Eine Strasse mit 10 % Steigung
steigt pro 100 m Horizontaldistanz 10 m an:
10m
α
100m
Die Verkehrsschilder sind von links nach rechts zu lesen. So kann man unterscheiden,
ob man eine Steigung oder ein Gefälle vor sich hat.
Aufgabe 1: Wie lang ist die Strecke, die der Lastwagen auf 100 m Horizontaldistanz
zurücklegt?
Aufgabe 2: Wie viel Höhe gewinnt der Lastwagen auf 3.5 km Horizontaldistanz?
Aufgabe 3: Wie viel Höhe gewinnt der Lastwagen auf 3.5 km effektiver Fahrstrecke?
Aufgabe 4: Wie gross ist der Winkel α?
Man nennt allgemein das Verhältnis zwischen der Höhendifferenz und der
Horizontaldistanz die Steigung. Steigungen bezeichnet man mit dem Buchstaben m.
Es ist also
∆y
m=
∆x
∆y
α
∆x
10
= 0.1 . Wenn die Steigung in Prozent
100
angegeben wird (wie das bei Strassen der Fall ist), muss man sie noch mit 100%
multiplizieren:
Im vorliegenden Fall ist die Steigung also m =
m = 0.1 × 100% = 10%.
Umgekehrt teilt man die Steigung durch 100%, wenn man sie als gewöhnliche Zahl
angeben will.
∆y
∆x
ist nicht nur die Steigung m, sondern auch der Tangens von α. α heisst daher
Steigungs-winkel:
tanα = m =
∆y
∆x
α: Steigungswinkel, m: Steigung
Aufgabe 5: Eine Zahnradbahn hat eine Steigung von 82%. Wie viel steigt sie
a) pro km Horizontaldistanz?
b) pro km Fahrtstrecke?
Lösungen: 1. 100.5 m 2. 350 m 3. 348.3 m 4. 5.71° 5. a) 820 m. b) 634 m.
Warum man Sinus, Cosinus und Tangens die trigonometrischen
Funktionen nennt
Eine Funktion ist – etwas vereinfacht gesagt – eine Rechenvorschrift, wie man aus
einer Zahl x eine andere Zahl y berechnet. Der Taschenrechner hat für einige
Funktionen Funktionstasten: Tippt man erst eine Zahl und dann die Funktionstaste, so
erhält man eine andere Zahl. Der Taschenrechner hat dabei die Rechenvorschrift
ausgeführt, welche durch die Funktion vorgeschrieben wird. Beispiele für solche
Funktionen sind die Quadratfunktion, die Wurzelfunktion und eben Sinus, Cosinus und
Tangens.
"Trigonometrische" Funktionen heissen Sinus, Cosinus und Tangens deswegen, weil
man sie bei Berechnungen in Dreiecken benötigt. Das Wort Trigonometrie setzt sich
aus drei Teilen zusammen, die alle aus dem Griechischen stammen: tria = drei, gonos
= Winkel, meter = Mass.
Berechnungen in Dreiecken (auch nicht-rechtwinkligen) sind von zentraler Bedeutung
bei der Landvermessung und der Herstellung von Landkarten. Unsere heutigen
genauen Karten sind das Ergebnis einer flächendeckenden Aufteilung des Landes in
Dreiecke, die wiederum in Unter-dreiecke und Unterunterdreiecke usw. aufgeteilt
werden.
Aufgabe: Lesen Sie mehr zu diesem Thema in Oskar Bär, Geographie der Schweiz, S.
214 – 223. Das Buch liegt auf dem Lehrerpult. Beantworten Sie dann folgende Fragen:
1. Wie ist das schweizerische Kilometer-Koordinatennetz aufgebaut? Warum befindet
sich der Nullpunkt dieses Koordinatensystems nicht in der Schweiz selbst?
2. Was ist das Hauptproblem, wenn man grosse Teile der Erde auf einer Karte
darstellen will?
3. Seit wann gibt es in der Schweiz genaue Landeskarten?
Rechenaufgaben
Pythagoras
mit
Höhensatz,
Kathetensatz
und
Satz
von
1. Berechnen Sie die fehlenden Stücke des rechtwinkligen Dreiecks ABC. Benutzen Sie
dafür die Beziehungen auf der Formelsammlung (ohne sin, cos und tan)!
.
a
b
h
.
p
q
c
a)
a
b
c
7
24
h
b)
c)
q
p
25
144
Flächeninhalt F
4
15
d)
3
e)
1.5
4
5
f)
2
8.5
2. Berechnen Sie die fehlenden Stücke des gleichschenkligen Dreiecks.
a)
a
h
5
5
b)
5
c)
1.5
s
Flächeninhalt
F
29
s
s
9
h
.
a
3. Berechnen Sie fehlenden Stücke des gleichseitigen Dreiecks.
a
a)
b)
c)
h
Flächeninhalt F
6
a
5
a
h
15
3
.
a
4. Berechnen Sie die Länge der Diagonalen in
a) einem Quadrat mit a = 5
b) einem Rechteck mit a = 8 und b = 6
5. Berechnen Sie die Länge der Raumdiagonale in
a) einem Würfel mit a = 5
b) einem Quader mit a = 8, b = 9 und c = 17
6. Ein gleichseitiges Dreieck hat den Flächeninhalt F = 75. Wie gross ist sein Umfang?
7. Berechnen Sie die Länge der fettgedruckten gestrichelten Linie im folgenden
Quader:
Mitte
240
225
360
8. Eine 10 m lange Leiter soll so an einen Fenstersims angelehnt werden, dass die
Leiterspitze genau auf den Fenstersims zu liegen kommt, der 9.55 m über dem
Boden liegt. Wie weit muss der Leiterfuss von der Hauswand entfernt sein?
9. In einem Rechteck kennen Sie die Diagonale (12 dm) und die Breite (7 dm). Wie
gross ist die Rechtecksfläche?
10.Von einem gleichschenkligen Trapez kennen Sie Seiten a = 9 m, b = d = 5 m und c
= 3 m. Berechnen Sie die Höhe des Trapezes.
c
d
h
b
.
a
11.Die Grundkante einer geraden, quadratischen Pyramide misst 4 m, die Seitenkante
5 m. Berechnen Sie die Höhe der Pyramide.
Rechenaufgaben mit Sinus, Cosinus und Tangens
Lösen Sie pro Schwierigkeitsstufe (blau, rot, schwarz) mindestens 3 Aufgaben!
Probetest
1. In einem rechtwinkligen Dreieck kennt man 2 der Grössen a, b, c, h, q, p, α, β; die
übrigen sind gesucht:
B
β p
b) p = 5, α = 30°
a) h = 1, q = 1
a
C
.
c

q
.
α
b
2. Konstruieren Sie ein rechtwinkliges Dreieck mit h = 2 cm, c = 5 cm. Konstruieren
Sie dann ein Quadrat mit dem gleichen Flächeninhalt (Anleitung: Ergänzen Sie das
Dreieck zunächst zu einem Rechteck).
α1
α2
α3
α4
3.
α3
α2
α1
200m
480m
520m
α4
220m
x
=
=
=
=
28.5°
23.8°
19.6°
27.7°
B
A
Von A aus (Höhe 420 m ü. Meer) soll die Höhe von B bestimmt werden. Die
Horizontaldistanzen sind durch Luftaufnahmen bekannt, die Winkel wurden
vermessen.
a) Berechnen Sie die Höhe von B.
b) Wie lang würde ein direkter Tunnel von A nach B (Strecke x)?
4. Ein Koffer ist 0.9 m lang, 0.7 m hoch und 0.3 m dick. Ist es möglich, darin eine 1.15
m lange und 1 cm dicke Stange unterzubringen?
5. Eine Pyramide hat die Grundkante a = 10 cm und
die Höhe h = 15 cm. Berechnen Sie den Inhalt einer
Seitenfläche sowie die Länge einer Seitenkante s.
s
h
a
a
6. Ein Blitz leuchtet unter einem Winkel von 30° über dem Horizont auf, 5 Sekunden
später hört man den Donner. Auf welcher Höhe über dem Boden befand sich der
Blitz? Die Schall-geschwindigkeit ist 340 Meter pro Sekunde.
7. Welche Fläche hat das Quadrat, wenn der Kreis
einen Radius von 4 cm hat?
8. Eine Bergbahn steigt auf 100 m Fahrtstrecke 84 m
an. Wie gross ist der Winkel der Schienen zur
Horizontalen?
A
Lösungen
Pythagoras in drei Dimensionen
1. D = 32 + 42 + 22 = 13
2. h = (21m) 2 − (4 m) 2 − (5 m) 2 = 20 m
3. D = 52 + 52 + 52 = 3 ⋅ 5 = 8.66
81
2
2
4. 81 = 3a = 3 ⋅ a = 3 ⋅ a ⇒ a =
5. 1002 =
3
= 46.77
a2
a2
a2
+ 63 ⇒ 1002 − 632 =
⇒ 6031=
⇒ 12062= a2 ⇒ a = 109.82
2
2
2
 d
 2
2
 a
 2
2
 a
 2
2
6. Anstelle von   =   +   =
 d
 2
2
 a
 2
2
a2
gilt jetzt
2
 b
 2
2
wie zuvor s2 =   + h2 =   +   + h2 =
2
2
2
 d
 a
 b
  =   +   . Daraus folgt ähnlich
 2
 2
 2
a2 b2
+
+ h2
4
4
Gleichschenklige Dreiecke und Pythagoras
1. h =
3
3
1
1
3
a=
⋅ 5 ⇒ F = ⋅ a⋅ h = ⋅ 5⋅
⋅ 5 = 10.83
2
2
2
2
2
Konstruktionsaufgaben mit rechtwinkligen und gleichschenkligen
Dreiecken
Aufgabe 1:
2. Lösung
h
p
q
c
2. Lösu ng
Aufgabe 2:
a2 = pc
a2 = 5⋅(5+2) = 35
b2 = qc
b2 = 2⋅(5+2) = 14
a=
b = 14 = 3.742
35 = 5.916
1. a)
Konstruktionsbeschreibung:
1. b = AC zeichnen
2. a = CB senkrecht zu b durch C
3. c = AB zeichnen
Lösung:
c = 5 cm
b)
Konstruktionsbeschreibung:
1. c = AB zeichnen
2. α bei A abtragen, das ergibt
einen Strahl b1 in Richtung von b
3. Thaleskreis k über c einzeichnen
4. b1 geschnitten mit k gibt C
5. a = BC zeichnen
Lösung:
a = 4 cm, b = 6.9 cm
c)
Konstruktionsbeschreibung:
1. Lösung:
(die Konstruktion ist auch im Theorieteil a = 6.09 cm, b = 3.45 cm
des Postens erklärt!):
2. Lösung
1. c = AB zeichnen
a = 3.45 cm, b= 6.09 cm
2. Parallele pc zu c im Abstand h zeichnen
3. Thaleskreis k über c einzeichnen
4. pc geschnitten mit k gibt C1 und C2
5. 1. Lösung: Dreieck ABC1, 2. Lösung: Dreieck ABC2
d)
Konstruktionsbeschreibung:
Lösung:
1. c = AB zeichnen
b = 10.9 cm
2. Kreis k1 um B mit Radius a = 5 cm
3. Thaleskreis k2 über c
4. k1 geschnitten mit k2 gibt C
5. Punkte A, B und C verbinden
e)
Konstruktionsbeschreibung:
Lösung:
1. h einzeichnen: h geht vom
a = 14 cm, b = 11.7, c = 18.3 cm
Punkt C zum Fusspunkt auf c,
der Fc heissen soll
2. Senkrechte zu h durch Fc ergibt
einen Strahl c1 in Richtung von c
3. Irgendwo eine Gerade a1 im
Winkel β = 40° zu c1 einzeichnen
4. a1 parallel verschieben, bis sie durch
C geht, diese Parallele soll a 2 heissen
5. a2 geschnitten mit c1 gibt B
6. Senkrechte a2 durch C (sie soll b1
heissen) zeichnen
7. b1 geschnitten mit c1 gibt A
8. Punkte A, B und C verbinden
f)
Konstruktionsbeschreibung:
1. h einzeichnen: h geht vom
Punkt C zum Fusspunkt auf c,
der Fc heissen soll
2. Senkrechte zu h durch Fc,
die c1 heissen soll
3. Kreis k um C mit Radius a = 6 cm
4. k geschnitten mit c1 gibt B
5. Senkrechte zu h durch C, die
Lösung:
b = 5.4 cm c = 8.0 cm
b1 heissen soll
6. b1 geschnitten mit c1 gibt A
7. Punkte A, B und C verbinden
2. a) Konstruktionsbeschreibung:
1. a = BC zeicnen
2. Kreis k1 mit Radius s um B
3. Kreis k2 mit Radius s um C
4. k1 geschnitten mit k2 gibt A
5. Punkte A, B und C verbinden
Lösung:
h = 6.5 cm, α = 42°, β = 69°
b) Konstruktionsbeschreibung:
Lösung:
1. a = BC zeichnen
s = 11.7 cm, α = 40°, β = 70°
2. M = Mittelpunkt von a konstruieren
3. h = MA senkrecht zu a auf M
4. Punkte A, B und C verbinden
c) Konstruktionsbeschreibung:
1. a = BC zeichnen
2. β von B aus abtragen ⇒ s1
3. β von B aus abtragen ⇒ s2
4. s1 geschnitten mit s2 gibt A
5. Punkte A, B und C verbinden
Lösung:
s = 3.9 cm, h = 2.5 cm, α = 100°
d) Konstruktionsbeschreibung:
Lösung:
1. a = BC zeichnen
s = 8.8 cm, h = 8.2 cm, β = 70°
2. h1 als Mittelsenkrechte von BC
konstruieren
3. Eine Gerade s1 im Winkel α/2 = 20°
zu h1 durch einem beliebigen Punkt
von h1 zeichnen.
4. s1 parallelverschieben, bis sie durch
C geht, die verschobene Gerade soll
s2 heissen
5. s2 geschnitten mit h1 gibt A
6. Punkte A, B und C verbinden
e) Konstruktionsbeschreibung:
Lösung:
1. h = MA (M = Mittelpunkt der
s = 9.8 cm, a = 11.2 cm, α = 50°
Seite a) zeichnen
2. Eine Senkrechte a1 zu h durch M
zeichnen
3. Eine Gerade s1 im Winkel α/2 = 35°
zu h durch A zeichnen
4. s2 wie s1, aber auf der anderen Seite von h
zeichnen
5. s1 geschnitten mit a1 gibt B (oder C)
6. s2 geschnitten mit a1 gibt C (oder B)
7. A, B und C verbinden
f) Konstruktionsbeschreibung:
1. h = MA (M = Mittelpunkt der
Seite a) zeichnen
Lösung:
s = 8.5 cm, a = 5.8 cm, β = 40°
2. Eine Senkrechte a1 zu h durch M
zeichnen
3. α = 180° – 2β konstruieren
4. Eine Gerade s1 im Winkel α/2 = 35°
zu h durch A zeichnen
5. s2 wie s1, aber auf der anderen Seite von h
zeichnen
6. s1 geschnitten mit a1 gibt B (oder C)
7. s2 geschnitten mit a1 gibt C (oder B)
8. A, B und C verbinden
g) Konstruktionsbeschreibung:
Lösung:
1. s = AB zeichnen
a = 15.9 cm, α = 83°, β = 48.5°
2. Thaleskreis k1 über s zeichnen
3. Kreis k2 mit Radius h = 9 cm um A
4. k1 geschnitten mit k2 gibt M
5. Strecke BM verdoppeln gibt C
6. A, B und C verbinden
3.
h) Konstruktionsbeschreibung:
1. s = AB zeichnen
2. Thaleskreis k über s zeichnen
3. Gerade a1 im Winkel β = 50° zu s
durch B zeichnen
4. a1 geschnitten mit k gibt M
5. Strecke BM verdoppeln gibt C
6. A, B und C verbinden
Lösung:
h = 7.7 cm, a = 12.9 cm, α = 80°
a)
Lösung:
Quadratseite = 4.1 cm.



(Die Skizze ist stark verkleinert)
b

a
b) Man konstruiert ein rechtwinkliges Dreieck mit den Katheten a = 4 cm und b
= 2.5 cm.
Aus dem Satz von Pythagoras ergibt sich, dass das
Hypotenusenquadrat das gesucht Quadrat ist.
Lösung: Die Kantenlänge ist 4.7 cm.
c) Man konstruiert ein rechtwinkliges Dreieck mit der Hypotenuse c = 4 cm und
der Kathete a = 2.5 cm. Aus dem Satz von Pythagoras ergibt sich, dass das
Quadrat über der anderen Kathete das gesuchte Quadrat ist.
Lösung: Die Kantenlänge
ist 3.1 cm.


4. a)

Die Skizze ist stark verkleinert. ist das
gegebene Quadrat, hat die Länge 3

cm.

Lösung:
2. Rechteckseite = 5.3 cm

b)
Die Skizze ist stark verkleinert. ist das
gegebene Quadrat, hat die Länge 10

cm,

also halb so viel wie der Umfang.

Lösung:
Die Rechtecksseiten sind 8 cm und 2
cm
c)









Die Skizze ist stark verkleinert. ist das gegebene Quadrat, hat die Länge
9 cm, somit hat das grössere rechtwinklige Dreieck die
Hypotenusenabschnitte 9 cm und 4 cm, das Verhältnis der
Hypotenusenabschnitte ist also gleich wie das Seitenver-hältnis des
gesuchten Rechtecks. Das kleinere rechtwinklige Dreieck ist ähnlich zum
grösseren (daher haben seine Hypotenusenabschnitte p und q ebenfalls
das Verhältnis 9 : 4), seine Höhe ist aber gerade 4 cm, daher ist das
Rechteck, das aus seinen Hypotenusenabschnitten gebildet wird, das
gesuchte Rechteck.
Lösung:
Die Seitenlängen sind 6 cm und 2.7 cm (exakt: 6 cm und 8/3 cm)
Steigung und Steigungswinkel
1.
(100m) 2 + (10 m) 2 = 100.5 m
10 m
x
=
⇒ x = 350m
100m 3500m
x
10 m
⇒ x = 348m
3. 3500m =
(100m) 2 + (10 m) 2
2.
4. tanα =
10 m
⇒ α = 5.7°
100m
5. a) 820 m
b) 634 m
Rechenaufgaben mit Höhensatz, Kathetensatz und Satz von
Pythagoras
1.
a
b
c
h
q
p
F
a)
7
24
25
6.72
23.04
1.96
84
b)
156
65
169
60
25
144
5070
c)
7.5
4
8.5
3.53
1.88
6.62
15
d)
6.71
3.35
7.5
3
1.5
6
11.25
5
4
1
4
10
e*)
f**)
oder
20
5
1.0071
8.4401
8.5
2
8.3867
0.1193
8.5
8.4401
1.0071
8.5
2
0.1193
8.3867
8.5
* : schwierig (freiwillig)
** : sehr schwierig (freiwillig)
2.
a
h
s
F
a)
5
5
5.59
12.5
b)
4
5
29
c)
12
1.5
6.18
10
9
3.
exakt
a
a)
4. a)
6
b)
2
3
⋅ 5
c)
2·
15
50 = 7.071
h
3·
F
3
5
45
9·
3
5
3
15·
3
gerunde
t
a)
a
h
F
6
5.196
15.588
b)
2.582
2.236
2.887
c)
7.746
6.708
25.981
b) 10
5. a) 75 = 8.660
b) 434 = 20.833
6. F =
3 2
4
a ⇒ a2 =
F ⇒ U = 3a = 39.48
4
3
7. D2 = 1802 + 2252 + 2402 = 140625⇒ D = 375
8. x2 = (10 m) 2 − (9.55 m) 2 = 8.7975m2 ⇒ x = 2.97 m
9. a2 + b2 = d2 ⇒ a = 95 dm
F = a ⋅ b = 7 dm⋅ 95 dm = 68.23 dm2
10.
h=√ (5 m) 2−( 3 m)2 =4 m
3m
5m
h
3m
3m
3m
c2 = (2 m)2 + (2 m)2
11.
c = √8 m
(5 m)2 = c2 + h2
h2 = (5 m)2 – c2 = 25 m2 – 8 m2 = 17
m2
h = 4.12 m
h
5m
c
.
.
4m
2m
2m
Rechenaufgaben mit Sinus, Cosinus und Tangens
blau
1.
2.
3.
4.
5.
6.
rot
137 m
1. 50°
a) 20.6° b) 128 m 2. 8 m
18°, 117.7 m
3. 0.53°
6.84°
4. 0.18°
123 m
5. 15.8°
2.38 m
6. auf dem Schild muss "13 %"
stehen
schwarz
1.
2.
3.
4.
5.
6.
7.
U = 147 cm, F = 1629
cm2
2865 m
Sparren 5 m, Breite 5.74
m
12.87 m
36 m, 42660 m3
α = 55.3°, β = 65.2°
1.73°
Probetest
1. a) b= √ 12 +1 2= √ 2
h 2 = pq ⇒ p=
b)
2
h
=1
q
c=p+q=2
a= √ c 2−b 2 =√ 2
h 1
sin α= = ⇒ α=45°
b √2
q = c – p = 15
b= √ c 2 −a 2 =17 .32
β = 90° – α = 45°
2.
h
c
3. a) tan α1 =
β=90 °−α=60 °
p
p
cos β= ⇒ a=
=10
a
cos β
a
a
cos β= ⇒ c=
=20
c
cos β
h
sin β= ⇒ h=a⋅sin β=8 . 66
a
Die Skizze ist massstäblich. Das Quadrat
wird am Schluss noch einmal halbiert, da
es nur so gross sein soll wie das rechtwinklige Dreieck mit c = 5 cm, h = 2 cm, nicht
so gross wie das daraus konstruierte Rechteck.
Δh1
⇒ ∆h1 = 200 m ⋅ tan α1 = 108.59 m
200 m
∆h2 = 200 m ⋅ tan α2 = 229.35 m
∆h3 = 200 m ⋅ tan α3 = 170.92 m
∆h4 = 200 m ⋅ tan α4 = 115.50 m
Höhe von B = Höhe von A + ∆h1 + ∆h2 − ∆h3 − ∆h4 = 471.52 m ≈ 472 m
√
b) x= ( 200 m+520 m+ 480 m+220 m)2 +(51. 52 m)2 =1421 m
√
4. Diagonallänge des Koffers: d = ( 0 .9 m)2 +( 0 . 7 m) 2 +(0 . 3 m) 2=1 . 179 m>1. 15 m⇒ Ja.
2
2
a
a
a
+
=
2
2
2
() ()
c 2=
5.
2
s 2=c 2 + h2 =
s=
√
a2 2
+h
2
a2 2
+ h =16 . 58 cm
2
Höhe der Seitenfläche:
s
a
2
2
( ) +h
a
ℓ= ( ) + h =15 .81 cm
√2
ℓ 2=
h

2
c
a/2
.
.
a/2
a
2
2
Inhalt der Seitenfläche:
F=
ℓ ⋅a
=79 . 06 cm 2
2
Entfernung des Blitzes: 5 ⋅ 340 m = 1700 m
6.
h
1700 m
h=850 m
sin 30 °=
17
h
00
m
30°
7.
a
F = a2 = r2 + r2 = 32 cm2
r
r
8.
10
α
0 m
84 m
84 m
100 m
α=57 . 14°
sin α=
                                           
W er k sta tt- P a ss
N a m e : ..........................
                            
Pythagoras, die
Wahrheit, und die
Ochsen *
Grundbegriffe in
rechtwinkligen und
gleichschenkligen
Dreiecken
Der Satz von
Pythagoras
und sein
Beweis
Pythagoreische
Halbkreise und
andere Figuren
*
Pythagoras
in drei
Dimensione
n
Der
Höhensatz
Gleich-schen
klige
Dreiecke
und
Pythagoras
Kongruent
e Dreiecke
Der
Kathetensatz
(Satz von
Euklid)
Konstruktions-au
fgaben mit
rechtwinkligen
und
gleichschenklige
n Dreiecken *
Formel
-samm
-lung *
Rechenaufgaben mit
Höhensatz, Kathetensatz
und Satz von Pythagoras
Pythagoras –
Mathematiker oder
Sektenführer? *
Wie sind Sinus, Cosinus
und Tangens definiert, und
was kann man damit
berechnen?
Sinus, Cosinus
und Tangens
bei
gleichschenklig
en Dreiecken
Wie hoch
ist unser
Schulhau
s? *
Steigung
und
Steigungs
-winkel
Warum man
Sinus, Cosinus
und Tangens die
trigonometrischen
Funktionen nennt
*
Rechenaufgaben mit
Sinus, Cosinus und
Tangens
Probetest
Prüfung
Freiwillige Posten sind mit einem Stern
markiert.
Pythagoras, die Wahrheit, und die Ochsen
Grundbegriffe in rechtwinkligen und gleichschenkligen Dreiecken
Kongruente Dreiecke
Pythagoras – Mathematiker oder Sektenführer?
Der Satz von Pythagoras und sein Beweis
Der Höhensatz
Der Kathetensatz (Satz von Euklid)
Wie sind Sinus, Cosinus und Tangens definiert, und was kann man damit berechnen?
Pythagoreische Halbkreise und andere Figuren
Pythagoras in drei Dimensionen
Gleichschenklige Dreiecke und Pythagoras
Konstruktionsaufgaben mit rechtwinkligen und gleichschenkligen Dreiecken
Formelsammlung
Sinus, Cosinus und Tangens bei gleichschenkligen Dreiecken
Wie hoch ist unser Schulhaus?
Steigung und Steigungswinkel
Warum man Sinus, Cosinus und Tangens die trigonometrischen Funktionen nennt
Rechenaufgaben mit Höhensatz, Kathetensatz und Satz von Pythagoras
Rechenaufgaben mit Sinus, Cosinus und Tangens
Probetest
Prüfung
GNU Free Documentation License
Version 1.3, 3 November 2008
Copyright © 2000, 2001, 2002, 2007, 2008 Free Software Foundation, Inc. <http://fsf.org/>
Everyone is permitted to copy and distribute verbatim copies of this license document, but changing it is not allowed.
0. PREAMBLE
The purpose of this License is to make a manual, textbook, or other functional and useful document "free" in the sense of freedom: to assure everyone the effective freedom to copy and redistribute it, with or without modifying it, either commercially or noncommercially. Secondarily, this License
preserves for the author and publisher a way to get credit for their work, while not being considered responsible for modifications made by others.
This License is a kind of "copyleft", which means that derivative works of the document must themselves be free in the same sense. It complements the GNU General Public License, which is a copyleft license designed for free software.
We have designed this License in order to use it for manuals for free software, because free software needs free documentation: a free program should come with manuals providing the same freedoms that the software does. But this License is not limited to software manuals; it can be used for any
textual work, regardless of subject matter or whether it is published as a printed book. We recommend this License principally for works whose purpose is instruction or reference.
1. APPLICABILITY AND DEFINITIONS
This License applies to any manual or other work, in any medium, that contains a notice placed by the copyright holder saying it can be distributed under the terms of this License. Such a notice grants a world-wide, royalty-free license, unlimited in duration, to use that work under the conditions
stated herein. The "Document", below, refers to any such manual or work. Any member of the public is a licensee, and is addressed as "you". You accept the license if you copy, modify or distribute the work in a way requiring permission under copyright law.
A "Modified Version" of the Document means any work containing the Document or a portion of it, either copied verbatim, or with modifications and/or translated into another language.
A "Secondary Section" is a named appendix or a front-matter section of the Document that deals exclusively with the relationship of the publishers or authors of the Document to the Document's overall subject (or to related matters) and contains nothing that could fall directly within that overall
subject. (Thus, if the Document is in part a textbook of mathematics, a Secondary Section may not explain any mathematics.) The relationship could be a matter of historical connection with the subject or with related matters, or of legal, commercial, philosophical, ethical or political position
regarding them.
The "Invariant Sections" are certain Secondary Sections whose titles are designated, as being those of Invariant Sections, in the notice that says that the Document is released under this License. If a section does not fit the above definition of Secondary then it is not allowed to be designated as
Invariant. The Document may contain zero Invariant Sections. If the Document does not identify any Invariant Sections then there are none.
The "Cover Texts" are certain short passages of text that are listed, as Front-Cover Texts or Back-Cover Texts, in the notice that says that the Document is released under this License. A Front-Cover Text may be at most 5 words, and a Back-Cover Text may be at most 25 words.
A "Transparent" copy of the Document means a machine-readable copy, represented in a format whose specification is available to the general public, that is suitable for revising the document straightforwardly with generic text editors or (for images composed of pixels) generic paint programs or (for
drawings) some widely available drawing editor, and that is suitable for input to text formatters or for automatic translation to a variety of formats suitable for input to text formatters. A copy made in an otherwise Transparent file format whose markup, or absence of markup, has been arranged to
thwart or discourage subsequent modification by readers is not Transparent. An image format is not Transparent if used for any substantial amount of text. A copy that is not "Transparent" is called "Opaque".
Examples of suitable formats for Transparent copies include plain ASCII without markup, Texinfo input format, LaTeX input format, SGML or XML using a publicly available DTD, and standard-conforming simple HTML, PostScript or PDF designed for human modification. Examples of
transparent image formats include PNG, XCF and JPG. Opaque formats include proprietary formats that can be read and edited only by proprietary word processors, SGML or XML for which the DTD and/or processing tools are not generally available, and the machine-generated HTML, PostScript
or PDF produced by some word processors for output purposes only.
The "Title Page" means, for a printed book, the title page itself, plus such following pages as are needed to hold, legibly, the material this License requires to appear in the title page. For works in formats which do not have any title page as such, "Title Page" means the text near the most prominent
appearance of the work's title, preceding the beginning of the body of the text.
The "publisher" means any person or entity that distributes copies of the Document to the public.
A section "Entitled XYZ" means a named subunit of the Document whose title either is precisely XYZ or contains XYZ in parentheses following text that translates XYZ in another language. (Here XYZ stands for a specific section name mentioned below, such as "Acknowledgements",
"Dedications", "Endorsements", or "History".) To "Preserve the Title" of such a section when you modify the Document means that it remains a section "Entitled XYZ" according to this definition.
The Document may include Warranty Disclaimers next to the notice which states that this License applies to the Document. These Warranty Disclaimers are considered to be included by reference in this License, but only as regards disclaiming warranties: any other implication that these Warranty
Disclaimers may have is void and has no effect on the meaning of this License.
2. VERBATIM COPYING
You may copy and distribute the Document in any medium, either commercially or noncommercially, provided that this License, the copyright notices, and the license notice saying this License applies to the Document are reproduced in all copies, and that you add no other conditions whatsoever to
those of this License. You may not use technical measures to obstruct or control the reading or further copying of the copies you make or distribute. However, you may accept compensation in exchange for copies. If you distribute a large enough number of copies you must also follow the conditions
in section 3.
You may also lend copies, under the same conditions stated above, and you may publicly display copies.
3. COPYING IN QUANTITY
If you publish printed copies (or copies in media that commonly have printed covers) of the Document, numbering more than 100, and the Document's license notice requires Cover Texts, you must enclose the copies in covers that carry, clearly and legibly, all these Cover Texts: Front-Cover Texts on
the front cover, and Back-Cover Texts on the back cover. Both covers must also clearly and legibly identify you as the publisher of these copies. The front cover must present the full title with all words of the title equally prominent and visible. You may add other material on the covers in addition.
Copying with changes limited to the covers, as long as they preserve the title of the Document and satisfy these conditions, can be treated as verbatim copying in other respects.
If the required texts for either cover are too voluminous to fit legibly, you should put the first ones listed (as many as fit reasonably) on the actual cover, and continue the rest onto adjacent pages.
If you publish or distribute Opaque copies of the Document numbering more than 100, you must either include a machine-readable Transparent copy along with each Opaque copy, or state in or with each Opaque copy a computer-network location from which the general network-using public has
access to download using public-standard network protocols a complete Transparent copy of the Document, free of added material. If you use the latter option, you must take reasonably prudent steps, when you begin distribution of Opaque copies in quantity, to ensure that this Transparent copy will
remain thus accessible at the stated location until at least one year after the last time you distribute an Opaque copy (directly or through your agents or retailers) of that edition to the public.
It is requested, but not required, that you contact the authors of the Document well before redistributing any large number of copies, to give them a chance to provide you with an updated version of the Document.
4. MODIFICATIONS
You may copy and distribute a Modified Version of the Document under the conditions of sections 2 and 3 above, provided that you release the Modified Version under precisely this License, with the Modified Version filling the role of the Document, thus licensing distribution and modification of the
Modified Version to whoever possesses a copy of it. In addition, you must do these things in the Modified Version:
A.
Use in the Title Page (and on the covers, if any) a title distinct from that of the Document, and from those of previous versions (which should, if there were any, be listed in the History section of the Document). You may use the same title as a previous version if the original
publisher of that version gives permission.
B.
List on the Title Page, as authors, one or more persons or entities responsible for authorship of the modifications in the Modified Version, together with at least five of the principal authors of the Document (all of its principal authors, if it has fewer than five), unless they release
you from this requirement.
C.
State on the Title page the name of the publisher of the Modified Version, as the publisher.
D.
Preserve all the copyright notices of the Document.
E.
Add an appropriate copyright notice for your modifications adjacent to the other copyright notices.
F.
Include, immediately after the copyright notices, a license notice giving the public permission to use the Modified Version under the terms of this License, in the form shown in the Addendum below.
G.
Preserve in that license notice the full lists of Invariant Sections and required Cover Texts given in the Document's license notice.
H.
Include an unaltered copy of this License.
I.
Preserve the section Entitled "History", Preserve its Title, and add to it an item stating at least the title, year, new authors, and publisher of the Modified Version as given on the Title Page. If there is no section Entitled "History" in the Document, create one stating the title, year,
authors, and publisher of the Document as given on its Title Page, then add an item describing the Modified Version as stated in the previous sentence.
J.
Preserve the network location, if any, given in the Document for public access to a Transparent copy of the Document, and likewise the network locations given in the Document for previous versions it was based on. These may be placed in the "History" section. You may omit a
network location for a work that was published at least four years before the Document itself, or if the original publisher of the version it refers to gives permission.
K.
For any section Entitled "Acknowledgements" or "Dedications", Preserve the Title of the section, and preserve in the section all the substance and tone of each of the contributor acknowledgements and/or dedications given therein.
L.
Preserve all the Invariant Sections of the Document, unaltered in their text and in their titles. Section numbers or the equivalent are not considered part of the section titles.
M.
Delete any section Entitled "Endorsements". Such a section may not be included in the Modified Version.
N.
Do not retitle any existing section to be Entitled "Endorsements" or to conflict in title with any Invariant Section.
O.
Preserve any Warranty Disclaimers.
If the Modified Version includes new front-matter sections or appendices that qualify as Secondary Sections and contain no material copied from the Document, you may at your option designate some or all of these sections as invariant. To do this, add their titles to the list of Invariant Sections in the
Modified Version's license notice. These titles must be distinct from any other section titles.
You may add a section Entitled "Endorsements", provided it contains nothing but endorsements of your Modified Version by various parties—for example, statements of peer review or that the text has been approved by an organization as the authoritative definition of a standard.
You may add a passage of up to five words as a Front-Cover Text, and a passage of up to 25 words as a Back-Cover Text, to the end of the list of Cover Texts in the Modified Version. Only one passage of Front-Cover Text and one of Back-Cover Text may be added by (or through arrangements made
by) any one entity. If the Document already includes a cover text for the same cover, previously added by you or by arrangement made by the same entity you are acting on behalf of, you may not add another; but you may replace the old one, on explicit permission from the previous publisher that
added the old one.
The author(s) and publisher(s) of the Document do not by this License give permission to use their names for publicity for or to assert or imply endorsement of any Modified Version.
5. COMBINING DOCUMENTS
You may combine the Document with other documents released under this License, under the terms defined in section 4 above for modified versions, provided that you include in the combination all of the Invariant Sections of all of the original documents, unmodified, and list them all as Invariant
Sections of your combined work in its license notice, and that you preserve all their Warranty Disclaimers.
The combined work need only contain one copy of this License, and multiple identical Invariant Sections may be replaced with a single copy. If there are multiple Invariant Sections with the same name but different contents, make the title of each such section unique by adding at the end of it, in
parentheses, the name of the original author or publisher of that section if known, or else a unique number. Make the same adjustment to the section titles in the list of Invariant Sections in the license notice of the combined work.
In the combination, you must combine any sections Entitled "History" in the various original documents, forming one section Entitled "History"; likewise combine any sections Entitled "Acknowledgements", and any sections Entitled "Dedications". You must delete all sections Entitled
"Endorsements".
6. COLLECTIONS OF DOCUMENTS
You may make a collection consisting of the Document and other documents released under this License, and replace the individual copies of this License in the various documents with a single copy that is included in the collection, provided that you follow the rules of this License for verbatim
copying of each of the documents in all other respects.
You may extract a single document from such a collection, and distribute it individually under this License, provided you insert a copy of this License into the extracted document, and follow this License in all other respects regarding verbatim copying of that document.
7. AGGREGATION WITH INDEPENDENT WORKS
A compilation of the Document or its derivatives with other separate and independent documents or works, in or on a volume of a storage or distribution medium, is called an "aggregate" if the copyright resulting from the compilation is not used to limit the legal rights of the compilation's users
beyond what the individual works permit. When the Document is included in an aggregate, this License does not apply to the other works in the aggregate which are not themselves derivative works of the Document.
If the Cover Text requirement of section 3 is applicable to these copies of the Document, then if the Document is less than one half of the entire aggregate, the Document's Cover Texts may be placed on covers that bracket the Document within the aggregate, or the electronic equivalent of covers if the
Document is in electronic form. Otherwise they must appear on printed covers that bracket the whole aggregate.
8. TRANSLATION
Translation is considered a kind of modification, so you may distribute translations of the Document under the terms of section 4. Replacing Invariant Sections with translations requires special permission from their copyright holders, but you may include translations of some or all Invariant Sections
in addition to the original versions of these Invariant Sections. You may include a translation of this License, and all the license notices in the Document, and any Warranty Disclaimers, provided that you also include the original English version of this License and the original versions of those notices
and disclaimers. In case of a disagreement between the translation and the original version of this License or a notice or disclaimer, the original version will prevail.
If a section in the Document is Entitled "Acknowledgements", "Dedications", or "History", the requirement (section 4) to Preserve its Title (section 1) will typically require changing the actual title.
9. TERMINATION
You may not copy, modify, sublicense, or distribute the Document except as expressly provided under this License. Any attempt otherwise to copy, modify, sublicense, or distribute it is void, and will automatically terminate your rights under this License.
However, if you cease all violation of this License, then your license from a particular copyright holder is reinstated (a) provisionally, unless and until the copyright holder explicitly and finally terminates your license, and (b) permanently, if the copyright holder fails to notify you of the violation by
some reasonable means prior to 60 days after the cessation.
Moreover, your license from a particular copyright holder is reinstated permanently if the copyright holder notifies you of the violation by some reasonable means, this is the first time you have received notice of violation of this License (for any work) from that copyright holder, and you cure the
violation prior to 30 days after your receipt of the notice.
Termination of your rights under this section does not terminate the licenses of parties who have received copies or rights from you under this License. If your rights have been terminated and not permanently reinstated, receipt of a copy of some or all of the same material does not give you any rights
to use it.
10. FUTURE REVISIONS OF THIS LICENSE
The Free Software Foundation may publish new, revised versions of the GNU Free Documentation License from time to time. Such new versions will be similar in spirit to the present version, but may differ in detail to address new problems or concerns. See http://www.gnu.org/copyleft/.
Each version of the License is given a distinguishing version number. If the Document specifies that a particular numbered version of this License "or any later version" applies to it, you have the option of following the terms and conditions either of that specified version or of any later version that
has been published (not as a draft) by the Free Software Foundation. If the Document does not specify a version number of this License, you may choose any version ever published (not as a draft) by the Free Software Foundation. If the Document specifies that a proxy can decide which future
versions of this License can be used, that proxy's public statement of acceptance of a version permanently authorizes you to choose that version for the Document.
11. RELICENSING
"Massive Multiauthor Collaboration Site" (or "MMC Site") means any World Wide Web server that publishes copyrightable works and also provides prominent facilities for anybody to edit those works. A public wiki that anybody can edit is an example of such a server. A "Massive Multiauthor
Collaboration" (or "MMC") contained in the site means any set of copyrightable works thus published on the MMC site.
"CC-BY-SA" means the Creative Commons Attribution-Share Alike 3.0 license published by Creative Commons Corporation, a not-for-profit corporation with a principal place of business in San Francisco, California, as well as future copyleft versions of that license published by that same
organization.
"Incorporate" means to publish or republish a Document, in whole or in part, as part of another Document.
An MMC is "eligible for relicensing" if it is licensed under this License, and if all works that were first published under this License somewhere other than this MMC, and subsequently incorporated in whole or in part into the MMC, (1) had no cover texts or invariant sections, and (2) were thus
incorporated prior to November 1, 2008.
The operator of an MMC Site may republish an MMC contained in the site under CC-BY-SA on the same site at any time before August 1, 2009, provided the MMC is eligible for relicensing.