Stromteilerregel
Werbung
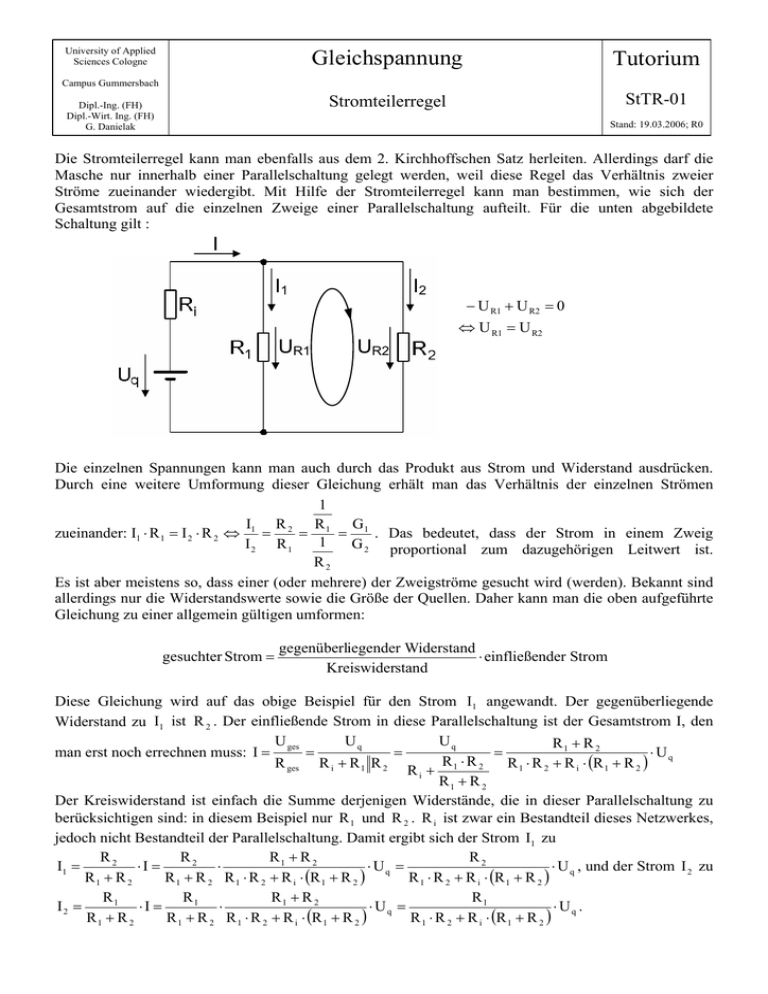
University of Applied Sciences Cologne Gleichspannung Tutorium Stromteilerregel StTR-01 Campus Gummersbach Dipl.-Ing. (FH) Dipl.-Wirt. Ing. (FH) G. Danielak Stand: 19.03.2006; R0 Die Stromteilerregel kann man ebenfalls aus dem 2. Kirchhoffschen Satz herleiten. Allerdings darf die Masche nur innerhalb einer Parallelschaltung gelegt werden, weil diese Regel das Verhältnis zweier Ströme zueinander wiedergibt. Mit Hilfe der Stromteilerregel kann man bestimmen, wie sich der Gesamtstrom auf die einzelnen Zweige einer Parallelschaltung aufteilt. Für die unten abgebildete Schaltung gilt : I I1 I2 − U R1 + U R2 = 0 ⇔ U R1 = U R2 UR1 UR2 Die einzelnen Spannungen kann man auch durch das Produkt aus Strom und Widerstand ausdrücken. Durch eine weitere Umformung dieser Gleichung erhält man das Verhältnis der einzelnen Strömen 1 I R G R zueinander: I1 ⋅ R 1 = I 2 ⋅ R 2 ⇔ 1 = 2 = 1 = 1 . Das bedeutet, dass der Strom in einem Zweig 1 I2 R1 G 2 proportional zum dazugehörigen Leitwert ist. R2 Es ist aber meistens so, dass einer (oder mehrere) der Zweigströme gesucht wird (werden). Bekannt sind allerdings nur die Widerstandswerte sowie die Größe der Quellen. Daher kann man die oben aufgeführte Gleichung zu einer allgemein gültigen umformen: gesuchter Strom = gegenüberliegender Widerstand ⋅ einfließender Strom Kreiswiderstand Diese Gleichung wird auf das obige Beispiel für den Strom I1 angewandt. Der gegenüberliegende Widerstand zu I1 ist R 2 . Der einfließende Strom in diese Parallelschaltung ist der Gesamtstrom I, den U ges Uq Uq R1 + R 2 man erst noch errechnen muss: I = = = = ⋅ Uq R1 ⋅ R 2 R ges R i + R 1 R 2 R 1 ⋅ R 2 + R i ⋅ (R 1 + R 2 ) Ri + R1 + R 2 Der Kreiswiderstand ist einfach die Summe derjenigen Widerstände, die in dieser Parallelschaltung zu berücksichtigen sind: in diesem Beispiel nur R 1 und R 2 . R i ist zwar ein Bestandteil dieses Netzwerkes, jedoch nicht Bestandteil der Parallelschaltung. Damit ergibt sich der Strom I1 zu R2 R2 R1 + R 2 R2 I1 = ⋅I = ⋅ ⋅ Uq = ⋅ U q , und der Strom I 2 zu R1 + R 2 R 1 + R 2 R 1 ⋅ R 2 + R i ⋅ (R 1 + R 2 ) R 1 ⋅ R 2 + R i ⋅ (R 1 + R 2 ) R1 R1 R1 + R 2 R1 I2 = ⋅I = ⋅ ⋅ Uq = ⋅ Uq . R1 + R 2 R 1 + R 2 R 1 ⋅ R 2 + R i ⋅ (R 1 + R 2 ) R 1 ⋅ R 2 + R i ⋅ (R 1 + R 2 ) University of Applied Sciences Cologne Gleichspannung Tutorium Stromteilerregel Ü-StTR-01 Campus Gummersbach Dipl.-Ing. (FH) Dipl.-Wirt. Ing. (FH) G. Danielak Stand: 19.03.2006; R0 Aufgabe 1: Bestimme sämtliche Ströme mittels Stromteilerregel. Folgende Werte liegen vor: R1 = 470Ω ; R2 = 390Ω ; R3 = 150Ω ; R4 = 220Ω I = 2,5A ; U = 20V a) b) I2 I2 I I I1 I1 c) d) I2 I I I2 I1 I1 Aufgabe 2: Bestimme sämtliche Ströme mittels Stromteilerregel, wenn U und alle Widerstände gegeben sind : a) I I2 b) I2 I I1 I1 U U University of Applied Sciences Cologne Gleichspannung Tutorium Stromteilerregel Ü-StTR-02 Campus Gummersbach Dipl.-Ing. (FH) Dipl.-Wirt. Ing. (FH) G. Danielak Stand: 19.03.2006; R0 Bestimme hier die Ausgangsspannung mit der Stromteilerregel. c) d) I I I1 I2 I2 I1 U U UA UA