Übungsblatt 12

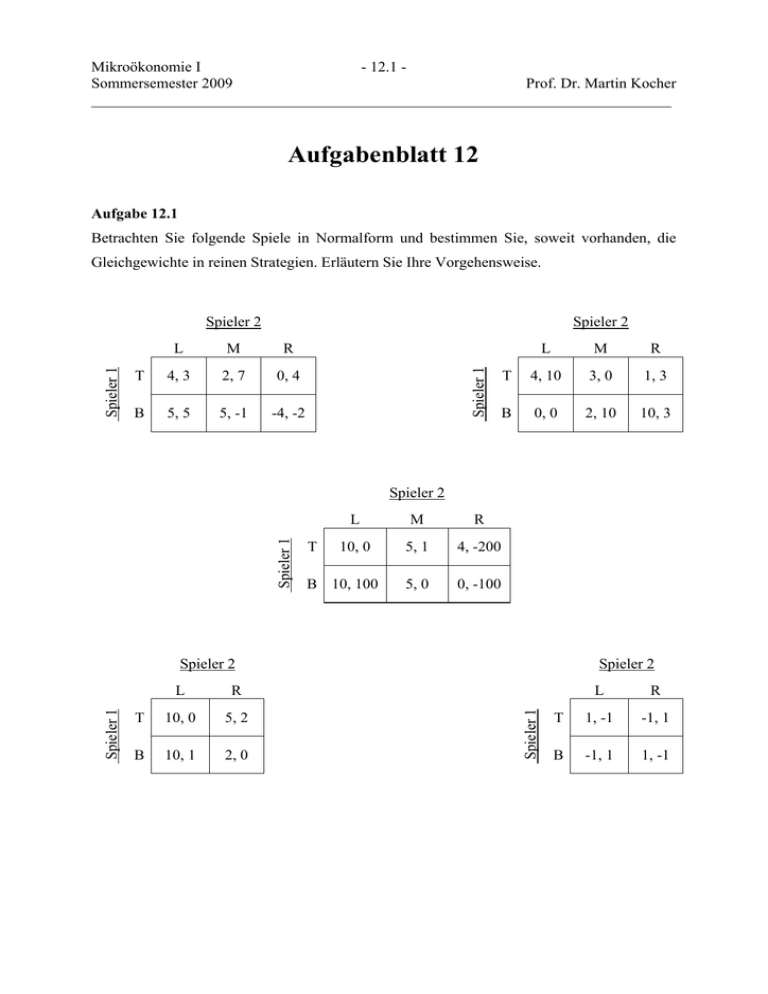
Mikroökonomie I
- 12.1 Sommersemester 2009
Prof. Dr. Martin Kocher
___________________________________________________________________________
Aufgabenblatt 12
Aufgabe 12.1
Betrachten Sie folgende Spiele in Normalform und bestimmen Sie, soweit vorhanden, die
Gleichgewichte in reinen Strategien. Erläutern Sie Ihre Vorgehensweise.
Spieler 2
L
M
R
T
4, 3
2, 7
0, 4
B
5, 5
5, -1
-4, -2
Spieler 1
Spieler 1
Spieler 2
L
M
R
T
4, 10
3, 0
1, 3
B
0, 0
2, 10
10, 3
T
L
M
R
10, 0
5, 1
4, -200
5, 0
0, -100
B 10, 100
Spieler 2
Spieler 2
L
R
L
R
T
10, 0
5, 2
T
1, -1
-1, 1
B
10, 1
2, 0
B
-1, 1
1, -1
Spieler 1
Spieler 1
Spieler 1
Spieler 2
Mikroökonomie I
- 12.2 Sommersemester 2009
Prof. Dr. Martin Kocher
___________________________________________________________________________
Aufgabe 12.2
Gegeben ist die folgende Auszahlungsmatrix mit den Strategien T, M, B für Spieler 1 und L,
C, R für Spieler 2:
Spieler 1
Spieler 2
L
C
R
T
2, 0
1, 1
4, 4
M
3, 3
0, 1
2, 2
B
1, 3
0, 2
3, 0
a) Vereinfachen Sie die Spielmatrix durch die Eliminierung streng dominierter Strategien.
b) Geben Sie die Nash-Gleichgewichte in reinen Strategien des Spiels an.
Aufgabe 12.3
Betrachten Sie das folgende Spiel in extensiver Form:
Spieler 1
A
B
Spieler 2
Spieler 2
L
4, 2
R
1, 1
L
5, 1
R
2, 3
a) Lösen Sie das Spiel durch Rückwärtsinduktion.
b) Bestimmen Sie die Normalform dieses Spiels.
c) Bestimmen Sie die Nash-Gleichgewichte in reinen Strategien. Sind alle NashGleichgewichte gleich plausibel?
Mikroökonomie I
- 12.3 Sommersemester 2009
Prof. Dr. Martin Kocher
___________________________________________________________________________
Aufgabe 12.4
Betrachten
Sie
das
folgende
dreistufige
Spiel
zwischen
einem
selbständigen
Softwareentwickler (S) und einem Konzern (K), für den S ein Programm entwickelt:
Auf Stufe 1 muss sich S entscheiden, ob er sich bei der Entwicklung des Programms anstrengt
oder nicht. Wenn S sich nicht anstrengt, so ist das Programm für K wertlos, das Spiel endet
und beide erhalten eine Auszahlung von 0. Wenn S sich anstrengt, so hat er Kosten von Euro
c unabhängig davon, ob er die Erfindung später an den Konzern verkauft oder nicht. Das
Programm hat in diesem Fall einen Wert von Euro v (wobei v / 2 > c > 1 ) für K und das Spiel
geht weiter auf Stufe 2.
Auf Stufe 2 macht K ein Kaufangebot an S. Das Angebot kann entweder hoch sein, so dass K
einen Preis von Euro v / 2 bietet, oder es ist niedrig, so dass K einen Preis von nur Euro 1
bietet.
Auf Stufe 3 entscheidet sich S, ob er das Angebot von K annimmt. Wenn er es annimmt, so
erhält er den angebotenen Kaufpreis, lehnt er ab, so erhält er kein Geld, da das Programm
firmenspezifisch ist und an niemand anderen verkauft werden kann.
a) Zeichnen Sie die extensive Form dieses Spiels.
b) Wie viele Strategien haben die beiden Spieler? Nennen Sie alle Strategien!
c) Wie viele Teilspiele hat dieses Spiel? Veranschaulichen Sie alle Teilspiele in der
extensiven Form!
d) Bestimmen Sie das teilspielperfekte Nash-Gleichgewicht dieses Spiels.
e) Angenommen, K könnte sich vor Beginn des Spiels entscheiden, ob er sich verpflichtet,
auf jeden Fall ein Angebot von Euro v / 2 an S zu machen, wenn dieser sich bei der
Entwicklung anstrengt. Wie sieht die extensive Form dieses Spiels aus? Welches
teilspielperfekte Gleichgewicht ergibt sich?
f) Würde K eine solche freiwillige Selbstverpflichtung eingehen wollen? Erläutern Sie kurz
verbal Ihre Antwort.