Aufgabe 5 (Bellman
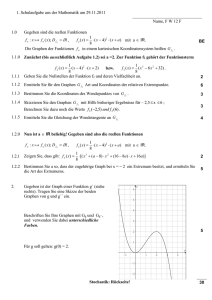
Werbung

Aufgabe 5 (Bellman-Ford)
Andreas Beer (086/9625203)
Patrick Traxler (931/0027287)
18. November 2004
1
Aufgabenstellung
1. Erläutern Sie das Verfahren von Bellman-Ford zur Bestimmung der kürzesten
Wege in einem gerichteten Graphen mit negativen Kantengewichten.
Abschnitt 2 weiter unten.
2. Rechnen Sie den Algorithmus an einem Beispiel vor.
Abschnitt 3 auf Seite 2.
3. Argumentieren Sie die Korrektheit des Verfahrens.
Abschnitt 4 (Seite 6).
4. Wie ist die Worst Case Laufzeit? Begründung.
Beides in Abschnitt 5 auf Seite 8.
2
Der Algorithmus
Der Bellman-Ford Algorithmus – auch bekannt als Moore-Algorithmus – wird in seiner
Urform verwendet um die kürzesten Wege von einem fixen Knoten s zu allen anderen
Knoten eines gegeben gerichteten Graphen G = (V, E) zu bestimmen. Eine einfache
Pseudo-Implementation ist in Abbildung 1 (Seite 2) zu sehen.
In d(x) wird die Länge des momentan kürzesten Weges von s nach x gespeichert. p(x)
ist der Vorgängerknoten auf diesem Weg. Beide Arrays werden in den Zeilen 3 und
4 auf offensichtliche Art initialisiert: Kein Knoten hat einen Vorgängerknoten und die
Distanz von s zu s ist natürlich Null. Alle anderen Knoten sind zur Zeit unerreichbar.
(Distanz Unendlich.)
Im Hauptteil des Algorithmus (Zeilen 6 bis 13) wird nun (|V | − 1)-mal für jede Kante
(u, v) untersucht, ob nicht vielleicht der Endknoten v über u schneller zu erreichen ist
als bisher. Falls ja, so werden die Werte entsprechend adaptiert.
Warum wird die äußere Schleife gerade (|V | − 1)-mal durchlaufen? Nun man sieht leicht, dass
man nicht mit weniger Iterationen auskommen kann. Ein entarteter Baum, in dem die Wurzel s
und jeder innere Knoten Weggrad Eins und alle Knoten Hingrad Null haben würde genau besagte
|V | − 1 Schritte benötigen, um den „kürzesten“ Weg von s zum Blatt zu finden.
Auf der anderen Seite kann ein kürzester Weg jeden Knoten nur maximal einmal enthalten.
(Vorausgesetzt natürlich, dass es keine Zyklen negativer Länge gibt. Dazu später mehr.) Also
wird man auch nicht mehr als |V | − 1 Iterationen brauchen.
1
1 # G = (V, E), s ∈ V , w : E → R;
3 d(s) ← 0, p(s) ← NIL;
4 foreach (v ∈ V \{s}) { d(v) ← ∞ , p(v) ← NIL; }
5
6 for (i = 1, . . . , |V | − 1) {
7
foreach ((u, v) ∈ E ) {
8
if (d(v) > d(u) + w(u, v)) {
9
d(v) ← d(u) + w(u, v);
10
p(v) ← u;
11
}
12
}
13 }
15 foreach ((u, v) ∈ E ) {
16
if (d(v) > d(u) + w(u, v)) {
17
return false ;
18
}
19 }
20 return true ;
# ∃ neg. Zyklus
# d(v) . . . min. Distanz s → v
Abbildung 1: Bellman-Ford für festes s
Auch für das Auffinden von negativen Zyklen wird besagtes |V | − 1 gerade ausreichen. Der
interessierte Leser ist eingeladen sich dies an einem Graphen, der nur aus einem negativen Zyklus besteht, selbst zu überlegen.
Die Behauptung ist nun, dass nach dem Durchlaufen dieser Schleifen die Länge des kürzesten
Wegs von s zu v in d(v) gespeichert ist. Finden wir in der Schleife von Zeile 15 trotzdem über u
einen kürzeren Weg zu v, so muss es wohl einen Zyklus negativer Länge (auf dem Weg von s zu
u) geben.
Finden wir keinen solchen Widerspruch, so wissen wir, dass es keinen Zyklus negativer
Länge gibt.1 Außerdem kennen wir mit d(v) die Länge des kürzesten Wegs von s nach v für alle
Knoten v. (Den Weg selbst können wir leicht mithilfe der p(v)’s rekonstruieren.
Damit wäre das Problem des Bestimmens der kürzesten Wege von s zu allen Knoten bewältigt.
Führt man diesen Algorithmus nun für alle s ∈ V aus, so erhält man entweder entsprechende
Information über eventuelle Zyklen negativer Länge, oder eine Matrix in der die kürzesten Wege
zwischen allen Knoten verzeichnet sind.
3
Das Beispiel
Die Vorlesungsunterlagen von Prof. Erickson [2] enthalten ein sehr anschauliches Beispiel, das
im folgenden präsentiert werden soll.
Direkt nach der Initialisierung (Zeile 5 in Abbildung 1 weiter oben) haben wir die in Abbildung
2 (Seite 3) dargestellte Situation: Nur Knoten s ist von s aus (mit Distanz Null) erreichbar. Alle
1 Genauer: Es gibt keinen Zyklus negativer Länge, der von s aus erreichbar ist. Streng genommen hat ja
niemand behauptet, dass alle Knoten von s aus erreichbar sind.
2
Abbildung 2: nach der Initialisierung
e
89:;
?>=<
∞ Og O
OOO
ooo
−8 ooo
OO2O
o
OOO
o
o
f
o
d
OO
o
woo o
1
?>=<
89:;
89:;
?>=<
∞ Og O
∞
7
OOO
ooo
OO0O
5 ooo
o
OOO b
ooo
OO
ooo
89:;
?>=<
−3
−3
7 ∞ Og
ooo O OOOOO −1
8 ooo
OOO
oo
OOO ooooo
O
?>=<
89:;
89:;
?>=<
∞ Og O
4
o7 ∞
OOO
o
o
a
c
OOO
ooo
O
ooo3
o
6 OOOO
o
oo
0
s
anderen liegen in unendlicher Weite.
Der Algorithmus wird nun alle Kanten auf eine Verbesserungsmöglichkeit überprüfen. Wir
wissen aber, dass dies nur bei Kanten, die von einem Knoten endlicher Distanz ausgehen, einen
Sinn macht. Diese Knoten werden im Weiteren doppelt rechteckig umrandet dargestellt.
Im ersten Durchlauf – dargestellt in Abbildung 3 (Seite 4) – haben wir drei Knoten gefunden,
die sich nun über einen kürzeren Weg ereichen lassen. Die Distanzen wurden aktualisiert und die
Vorgänger entsprechend auf s gesetzt.
Man kann sich leicht überlegen, dass die (momentan) kürzesten Wege von s aus einen Baum
bilden.2 Dieser Baum wird in den folgenden Graphen durch gewellte Kanten dargestellt. Wie
eingangs erwähnt ergeben sich besagte kürzeste Wege durch die jeweiligen p(v) Einträge der
einzelnen Knoten v.
Es wird angenommen, dass die Wahl der betrachteten Kanten im zweiten Schritt – siehe Abbildung 4 auf Seite 4 – gleichzeitig bzw. in einer etwas unglücklichen Reihenfolge erfolgt: Würde
zuerst die Kante (c, b) betrachtet werden, so könnten die Gesamtdistanzen zu den Knoten d und
f noch niedriger gesetzt werden. Man würde sich also „einen Schritt ersparen“.
Auf jeden Fall wird in diesem Schritt (über c) ein neuer kürzester Weg zu b gefunden. Nachdem alle Distanzen und Vorgänger entsprechend gesetzt wurden geht es mit Schritt Drei in Abbildung 5 (Seite 5) weiter.
Die weiteren Abbildungen sprechen eigentlich für sich: In jedem Schritt werden alle Kanten auf
eine eventuelle Verbesserungsmöglichkeit untersucht.
Die oben erwähnte (etwas verspätete) Aktualisierung der Distanz von b pflanzt sich im dritten Schritt (Abbildung 5, Seite 5) zu f fort und erreicht im vierten Schritt (Abbildung 6 auf Seite
5) Knoten e.
Im fünften Schritt (Abbildung 7 auf Seite 6) führt sie zu einem besseren Weg nach d. Im sechsten
2 Streng genommen können bei nullwertigen Kanten auch Zyklen entstehen. Diese kann man aber ohne
größere Schwierigkeiten aufbrechen.
3
Abbildung 3: nach dem 1-ten Durchlauf
e
89:;
?>=<
∞ Og O
OOO
ooo
−8 ooo
OO2O
o
OOO
oo
f
o
d
OO
o
o
o
w
1
?>=<
89:;
89:;
?>=<
o
∞ Og O
7 ∞
OOO
ooo
OO0O
5 ooo
o
OOO b
ooo
OO
ooo
−3
−3
7 4 gO
ooo O O OOOOO −1
8 ooo
O
OOO
oo
O
OOO oooo
O
o
O
4
6 g g'
O
7w 7 3
g' g'
c
a
7w 7w
O
g' g'
w
7
7w
O
'
g
w
7
3
g' g'
6
7w 7w
89:;
?>=<
0
s
Abbildung 4: nach dem 2-ten Durchlauf
e
89:;
?>=<
∞
Og OO
OOO 2
ooo
−8 ooo
OOO
o
o
OOO
o
f
o
d
o
O
o
wo
o
1
9
4 g g'
7
g' g' 0
7w 7w
5 7w 7w
g' g'
g' g'
7w 7w
g' b 7w 7w
−3
7 2 g
ooo O 'g 'g 'g −1
o
o
'g 'g
ooo
g' 'g
oooo
'g o
?>=<
89:;
89:;
?>=<
4
6 g g'
7 3
7w 7w
g' g'
7
w
a
c
7w
g' g'
7w 7w 3
w
7
6 g' g' g'
7w
89:;
?>=<
0
s
−3
8
4
Abbildung 5: nach dem 3-ten Durchlauf
e
11 g 'g
oo
'g 'g 2
'g 'g
o
o
o
'g 'g
f
o
o
'g
o
wo
1
og
7 7
g' g'
7w 7w
g' g' 0
5 7w 7w
g' g'
7w
g' g' b 7w 7w 7w
89:;
?>=<
−3
oo7 2O g g' g'
o
o
g' g' −1
8 oo
o
g' g'
ooo
g' g' ooo
89:;
?>=<
4
7 3
gOOO
7w 7w
OOO
w
7
c
w
7
OOO
7w
w
7
O
OOO
3
6
7w 7w
89:;
?>=<
0
s
−8 ooo
d
2
O
O
O
−3 O
O
O
O
1
a
Abbildung 6: nach dem 4-ten Durchlauf
e
9 g 'g
oo
'g 'g 2
'g 'g
o
o
'g 'g
oo
d
o
'g
o
w
o
1
?>=<
89:;
2 g o g'
w
7
g' g' 0
7w
O
5 7w 7w
g' g'
w
7
O
g' g'
w
7
O
g' b 7w 7w
89:;
?>=<
−3 O
7 2 g
O
ooo O g' g' g' −1
O
8 ooo
g' g'
O
oo
g' g'
oooo
g'
4
−1 gO
w
7
OOO
7w 7w
OOO
a
7w 7w
O
w
7
O
OOO
3
6
7w 7w
89:;
?>=<
0
−8 oooo
s
5
89:;
?>=<
7 7
f
−3
89:;
?>=<
3
7
c
Abbildung 7: nach dem 5-ten Durchlauf
e
89:;
?>=<
9 g 'g
7w 7w
'g 'g 2
−8 7w 7w
'g 'g
w7
7
w
'g 'g
w7
d
'g
wo w7
1
1 gOO
w
7
OOO
7w
O
5 7w 7w
OO0O
7w
OOO b
O
w
7
OO
O
7w 7w
89:;
?>=<
−3 O
2
g
7
O
ooo O g' g' g' −1
O
8oooo
g' g'
o
O
g' g'
ooooo
g'
@ABC
GFED
4
−1 Og O
w
7
OOO
7w 7w
a
OOO
7w 7w
O
w
7
O
OOO
3
6
7w 7w
89:;
?>=<
0
s
89:;
?>=<
7 7
f
−3
89:;
?>=<
7 3
c
und letzten Schritt (Abbildung 8, Seite 7) gibt es schlussendlich noch eine Aktualisierung der
Distanz von a.
Man sieht, dass der kürzeste Weg von s nach a über alle anderen Knoten des Graphen läuft.
Es waren also wirklich die eingangs erwähnten |V | − 1 Schritte notwendig um alle kürzesten
Wege zu berechnen.
4
Die Korrektheit
Frei nach dem Motto „Talk is cheap!“ wollen wir uns nun der Korrektheit dieses Algorithmus
zuwenden. Zuerst einmal ist leicht zu sehen, dass unerreichbare Knoten Distanz ∞ haben.
Behauptung 1. Ein Knoten v ist genau dann nicht von s aus erreichbar, wenn seine Distanz
nach Ablauf des Algorithmus mit ∞ angegeben wird.
Beweis. Die Distanz aller Knoten (außer s) wird mit ∞ initialisiert und nur dann geändert, wenn
besagter Knoten über einen seiner Vorgänger erreicht werden kann.
⇒ Da v aber nicht von s aus erreichbar ist, lässt sich auch keiner seiner Vorgänger von s
aus erreichen. Somit bleibt während aller |V | − 1 Schritte die Distanz von v gleich ∞.
⇐ Die Distanz von v kann nur dann ∞ bleiben, wenn wir v nicht innerhalb von |V | − 1
Durchläufen erreichen können. Wir wissen aber, dass der längste kürzeste3 Weg in einem Graphen jeden Knoten nur maximal einmal enthalten darf. Wenn wir v also nicht innerhalb von
|V | − 1 Schritten erreicht haben, so ist v von s aus überhaupt nicht erreichbar. Wenden wir uns nun dem interessantesten Teil der Korrektheit zu.
Behauptung 2. Enthält (V, E) keinen negativen Zyklus, der von v aus erreichbar ist, so ist d(v)
nach Ablauf des Algorithmus die minimale Distanz von s nach v (δ(s, v)).
3 ‚Kürzeste‘
bezieht sich in diesem Fall nur auf die Anzahl der Kanten.
6
Abbildung 8: Endergebnis
e
89:;
?>=<
9 g 'g
7w 7w
'g 'g 2
−8 7w 7w
'g 'g
w7
7
w
'g 'g
d
w7 w7
'g
w
1
?>=<
89:;
o
1 gOOO
w
7
7w
OOO 0
O
5 7w 7w
OOO
7w
O
w
7
OOO b
O
7w 7w
O
89:;
?>=<
−3 O
2
7
g
O
ooo O g' g' g' −1
O
8oooo
g' g'
o
O
g' g'
ooooo
g'
@ABC
GFED
4
−2 Og O
w
7
OOO
7w 7w
a
OOO
7w 7w
O
w
7
O
OOO
3
6
7w 7w
89:;
?>=<
0
s
89:;
?>=<
7 7
f
−3
89:;
?>=<
7 3
c
Beweis. Ist v nicht von s aus erreichbar, so sind wir bereits mit Satz 1 von Seite 6 fertig. Es
existiere also ein Pfad4 von s nach v und
s = v0 , v1 , v2 , . . . , vk−1 , vk = v
sei der5 kürzeste dieser Wege. Wir wissen, dass k ≤ |V | − 1 gilt.
Können wir nun zeigen, dass nach dem i-ten Durchlauf
d(v j ) = δ(s, v j )
j = 0, 1, . . . , i
gilt, so hätten wir unsere Behauptung bewiesen: Spätestens nach der (|V | − 1)-ten Iteration wäre
d(vk ) = d(v) = δ(s, v).
Unser Mittel zum Zweck wird natürlich die vollständige Induktion sein.
Anfang: i = 0 d(s) ist korrekterweise Null.
Voraussetzung: Für festes i gelte
d(v j ) = δ(s, v j )
j = 0, 1, . . . , i.
Schluß: i i + 1 Im (i + 1)-ten Durchlauf wird unter anderem (vi , vi+1 ) betrachtet. Somit gilt
nach dieser Iteration sicher
d(vi+1 )
≤
=
=
d(vi ) + w(vi , vi+1 )
δ(s, vi ) + w(vi , vi+1 )
δ(s, vi+1 ).
(Induktionsvoraussetzung)
(kürzester Weg)
Die letzte Gleichheit folgt daraus, dass v0 , v1 , . . . , vk ein kürzester Weg ist. Insbesondere
ist also der kürzeste Weg von s nach vi+1 derjenige, der über vi läuft.
4 Damit
5 Ist
so ein Pfad existiert muss angenommen werden, dass kein Zyklus negativer Länge existiert.
der kürzeste Weg nicht eindeutig, so wählen wir zufällig einen der in Frage kommenden Pfade aus.
7
Summa summarum wissen wir also, dass nach dem (i+1)-ten Durchlauf zumindest d(vi+1 ) ≤
δ(s, vi+1 ) gilt. Da d(vi+1 ) aber nicht echt kleiner sein kann,6 muss die Gleichheit gelten.
Laut Konstruktion des Algorithmus können die Werte in d(v) nie zunehmen. Wir wissen somit
also, dass uns auch während bzw. nach allen übrigen Iterationen der korrekte Wert δ(s, v) in
d(v) erhalten bleibt. Abschließend wollen wir uns noch Zyklen negativer Länge zuwenden.
Behauptung 3. Der Algorithmus informiert uns genau dann über einen Zyklus negativer Länge,
wenn ein solcher existiert.
Beweis. Existieren keine Zyklen negativer Länge, so wissen wir aus Satz 2 (Seite 6), dass d(v) =
δ(s, v) ∀v gilt. Klarerweise ist die Länge des minimalen Weges nie größer als die eines beliebigen.
Mit anderen Worten gilt
d(v) ≤ d(u) + w(u, v)
∀(u, v) ∈ E
und der Algorithmus meldet (richtigerweise) keinen Zyklus.
Sei nun v0 , v1 , . . . , vk , vk+1 = v0 ein Zyklus negativer Länge. Dann gilt logischerweise
k
∑ w(vi , vi+1 ) < 0.
i=0
Der Beweis läuft nun indirekt: Angenommen wir erhalten keine Rückmeldung über die Existenz
des Zyklus. Dann muss aber wiederum
d(v) ≤ d(u) + w(u, v)
∀(u, v) ∈ E
gelten. Einsetzen, subtrahieren und aufsummieren führt uns nun zu
d(vi+1 )
d(vi+1 ) − d(vi)
∑ki=0 d(vi+1 ) − d(vi )
≤
≤
d(vi ) + w(vi , vi+1 )
w(vi , vi+1 )
i = 0, . . . , k
i = 0, . . . , k
≤
∑ki=0 w(vi , vi+1 )
(Teleskopsumme)
v0
k
z}|{
d(vk+1 ) − d(v0 )
|
{z
}
=0
≤
∑ w(vi , vi+1 )
i=0
|
{z
<0
}
und somit zu einem Widerspruch. Vorausgesetzt dass ein negativer Zyklus existiert, werden wir
also auch über dessen Existenz informiert. Diese drei Sätze – Satz 1 von Seite 6, Behauptung 2 (Seite 6) und Aussage 3 von weiter oben –
liefern uns in Summe die gesuchte Korrektheit des Algorithmus.
Natürlich ist somit auch der Gesamtalgorithmus (also das Hintereinanderausführen für jeden
Knoten) korrekt.
5
Die Laufzeit
Diese lässt sich ganz einfach aus der Pseudo-Implementation in Abbildung 1 auf Seite 2 ersehen:
Zuerst wird |V | mal initialisiert, danach durchlaufen wir (ca.) |V | mal eine Schleife in der wir |E|
mal etwas überprüfen. Zum Schluss wird abermals |E| mal nachgeschaut.
In Summe erhalten wir für die Berechnung der kürzesten Wege eines Knotens zu allen anderen einen Aufwand von
O(|V | + |V |·|E| + |E|) = O(|V |·|E|).
6 d(v) ist ja immer die Länge des kürzesten bisher gefundenen Weges von s nach v. Diese kann logischerweise nie kleiner als die des allerkürzesten welchen sein.
8
Schlussendlich werden diese Berechnungen für jeden Knoten ausgeführt, was zu einer Worst
Case Laufzeit von
O(|V |·|V |·|E|) = O(|V |2 ·|E|)
führt.
Literatur
[1] B RAINY E NCYCLOPEDIA: Bellman-Ford algorithm.
http://tinyurl.com/5kbrr.
[2] E RICKSON , J EFF: Combinatorial Algorithms. uploaded at
http://compgeom.cs.uiuc.edu/~jeffe/teaching/373/, Fall 2002. Lecture 11: Shortest Paths. 2
[3] K RUMKE , S VEN O LIVER, H ARTMUT N OLTEMEIER, S TEFAN S CHWARZ und H ANS C HRISTOPH W IRTH: Graphentheoretische Konzepte und Algorithmen. Skriptum zur gleichnamigen Vorlesung an der Universität Würzburg, 9. März 2000.
9