Locker Aufsteigen Mathematik 2-Seite 29

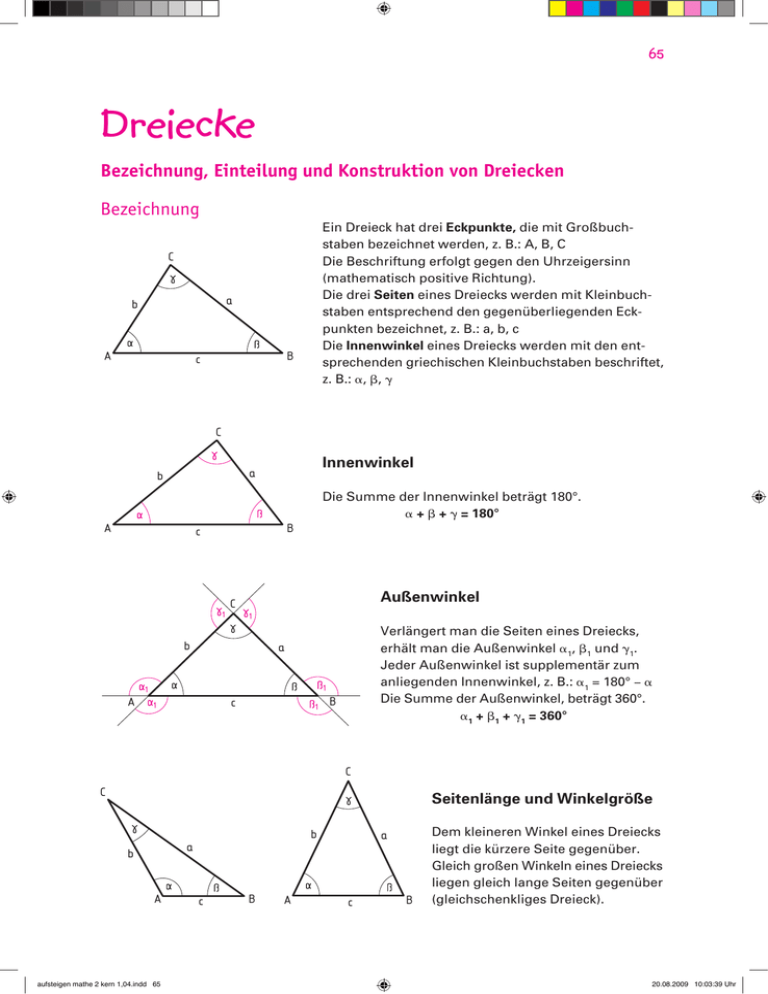
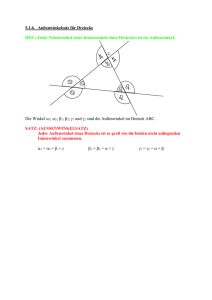
Kopfzeile
65
Dreiecke
Bezeichnung, Einteilung und Konstruktion von Dreiecken
Bezeichnung
Ein Dreieck hat drei Eckpunkte, die mit Großbuch­
staben bezeichnet werden, z. B.: A, B, C
Die Beschriftung erfolgt gegen den Uhrzeigersinn
(mathematisch positive Richtung).
Die drei Seiten eines Dreiecks werden mit Kleinbuchstaben entsprechend den gegenüberliegenden Eckpunkten bezeichnet, z. B.: a, b, c
Die Innenwinkel eines Dreiecks werden mit den entsprechenden griechischen Kleinbuchstaben beschriftet,
z. B.: a, b, g
C
a
b
A
B
c
C
Innenwinkel
a
b
Die Summe der Innenwinkel beträgt 180°.
a + b + g = 180°
A
B
c
1
Außenwinkel
C
1
b
1
1
A
Verlängert man die Seiten eines Dreiecks,
erhält man die Außenwinkel a1, b1 und g1.
Jeder Außenwinkel ist supplementär zum
anliegenden Innenwinkel, z. B.: a1 = 180° - a
Die Summe der Außenwinkel, beträgt 360°.
a1 + b1 + g1 = 360°
a
c
1
1
B
C
C
Seitenlänge und Winkelgröße
b
a
b
A
aufsteigen mathe 2 kern 1,04.indd 65
c
B
A
a
c
B
Dem kleineren Winkel eines Dreiecks
liegt die kürzere Seite gegenüber.
Gleich großen Winkeln eines Drei­ecks
liegen gleich lange Seiten gegen­­über
(gleichschenkliges Dreieck).
20.08.2009 10:03:39 Uhr
66
Dreiecke
Einteilung
nach den Seiten
gleichseitiges Dreieck
gleichschenkliges Dreieck
C
C
b
b
a
A
ungleichseitiges Dreieck
C
A
B
c
a
b
a
A
alle drei Seiten sind gleich lang a = b = c
B
c
B
c
zwei Seiten sind gleich lang a = b
alle Seiten sind
verschieden lang
rechtwinkliges Dreieck
stumpfwinkliges Dreieck
nach den Winkeln
spitzwinkliges Dreieck
C
C
C
b
a
b
A
A
c
a
a
b
B
c
B
alle Winkel sind spitze Winkel
a < 90°, b < 90°, g < 90°
A
ein Winkel ist ein rechter Winkel
g = 90°
B
c
ein Winkel ist ein
stumpfer Winkel
a > 90°
Konstruktion
Um ein Dreieck konstruieren zu können, muss die Summe zweier Seitenlängen größer
sein als die dritte Seitenlänge.
C
Dreiecke, von denen man drei Seitenlängen kennt:
a
b
nABC, gegeben: a = 4 cm,
b = 3 cm,
c = 5 cm
A
1. Beginne mit c = AB
2. Nimm die Länge der Seite b bzw. der Seite a
in den Zirkel und zeichne einen Kreis­bogen.
3. Der Schnittpunkt der Bögen ist der
Punkt C.
c
B
C
a
b
A
c
B
Wenn du das Dreieck auf einem anderen Blatt Papier nochmals zeichnest erhältst du ein
deckungsgleiches (kongruentes) Dreieck. Dreiecke sind kongruent, wenn sie in den drei
Seitenlängen übereinstimmen = Seiten-Seiten-Seiten-Satz: SSS-Satz.
aufsteigen mathe 2 kern 1,04.indd 66
20.08.2009 10:03:41 Uhr