Waermelehre-2-2
Werbung

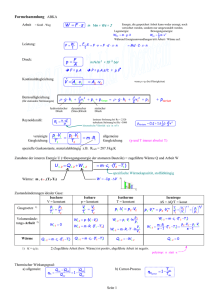
Jan Philip Nissen und Francis Wilken 27.11.2006 Physikalisches Praktikum für Anfänger - Teil 1 Gruppe 2 – Wärmelehre 2.2 Spezifische und latente Wärmen 1 Einleitung Die spezifische Wärme von Wasser gibt an, wieviel Energie man zu 1 kg Wasser zuführen muss, um diese um 1°C zu erwärmen. Beim Kochen ist diese Zahl ein leider nicht zu verändernder Kostenfaktor. Wenn man die spezifische Wärme c kennt, welche bei Wasser temperaturabhängig ist, so kann man berechnen, wie viel Energie (Arbeit) man mindestens aufbringen muss, um den Topf mit Wasser zum Sieden zu bringen. Mit Hilfe der latenten Wärme von Wasser können wir außerdem berechnen, wie viel Energie man mindestens aufbringen muss, um das Wasser vollständig zu Wasserdampf zu erhitzen. Dabei muss man allerdings noch die Abwärme an die Umgebung berücksichtigen. Die latente Wärme (Verdampfungswärme) gibt nämlich an, wie viel Energie man aufbringen, um eine 1 kg Wasser zum Verdampfen zu bringen, ohne dass die Temperatur dabei ansteigt. Latent heißt sie deshalb, weil die Aufnahme bzw. Abgabe dieser Wärme nicht zu einer Temperaturänderung führt. Die latente Wärme spielt auch in der Meteorologie eine wichtige Rolle, in Bezug auf die Phasenübergänge des Wassers in der Erdatmosphäre. Auf einer feuchten Erdoberfläche oder gar Wasserfläche wird ein Großteil der Sonnenenergie in die Verdunstung von Wasser investiert. Dabei werden 2257 Kilojoule pro Kilogramm Wasser umgesetzt. Eine Änderung der Lufttemperatur tritt dabei nicht auf, die Energie wird also sozusagen im gasförmigen Aggregatzustand des Wassers gespeichert. Die große spezifische Wärmekapazität von Wasser hat eine wichtige Bedeutung für das Klima unserer Erde. Das Meer speichert im Sommer infolge seiner hohen spezifischen Wärmekapazität bedeutende Energiemengen, ohne sich dabei stark zu erwärmen. Diese Energie wird im Winter wieder abgegeben. Das Klima am Meer ist daher das ganze Jahr über relativ ausgeglichen. Die spezifische Wärme von Wasser: – fest(0°C) 2,060 – flüssig 4,183 – gasförmig 2,020 Jan Philip Nissen und Francis Wilken 27.11.2006 2 Aufbau Die spezifische Wärme von Wasser Das Kalorimeter wird mit 120g destillierten Wasser gefüllt. Von nun an wird alle 30 Sekunden die Temperatur T notiert. Nach 3 Minuten wird die Heizung eingeschaltet und erwärmt. Nach einer gewissen Zeit wird die Heizung ausgeschaltet und wieder 3 Minuten gewartet. Dabei werden die Zeit t, die Spannung U und die Stromstärke I notiert. Von der Spannung und der Stromstärke wird nachher der Mittelwert gebildet. Die Schmelzwärme des Wassers Bei diesem Versuch wird ein ähnliches Kalorimeter verwendet wie beim vorigen Versuch. Das Kalorimeter wird mit 120g destillierten Wasser gefüllt. Von nun an wird alle 30 Sekunden die Temperatur T notiert. Nach 3 Minuten werden ein oder zwei Eiswürfel in das Wasser gelegt. Wenn das Eis komplett geschmolzen ist wird wieder 3 Minuten gewartet. Dabei wird immer auch die Zeit t notiert. Spezifische Wärme von Metallen Bei diesem Versuch wird ein ähnliches Kalorimeter verwendet wie beim vorigen Versuch. Das Kalorimeter wird mit 120g destillierten Wasser gefüllt. Nach 3 Minuten wird das bereits erhitzte Metall in das Wasser gegeben. Dabei wird in kurzen Abständen die Temperatur gemessen. Wenn die Temperatur sich angeglichen hat wird wieder 3 Minuten gewartet. Jan Philip Nissen und Francis Wilken 27.11.2006 3 Die spezifische Wärme von Wasser - Messwerte Durchführung 1 t /min U /V I /A T /° C Jan Philip Nissen und Francis Wilken 27.11.2006 Durchführung 2 t /min U /V I /A T /° C Jan Philip Nissen und Francis Wilken 27.11.2006 4 Die spezifische Wärme von Wasser - Auswertung Als erstes wird der Mittelwert von der Stromstärke I berechnet. Dies geschieht nach folgender Formel: n I = 1⋅∑ I k n k=1 Nun wird der Mittelwert von der Spannung U berechnet: n 1 U = ⋅∑ U k n k =1 Jetzt lesen wir die Werte für T aus dem Graphen ab: Wir stellen die Formel (2) um: 1 U⋅I⋅t Heiz c= ⋅ −W m T m=120 g W =40 J K Jan Philip Nissen und Francis Wilken 27.11.2006 5 Die Schmelzwärme des Wassers - Messwerte Durchführung 1 t /min T /° C t /min T /° C Jan Philip Nissen und Francis Wilken 27.11.2006 Durchführung 2 t /min T /° C t /min T /° C Jan Philip Nissen und Francis Wilken 27.11.2006 6 Die Schmelzwärme des Wassers - Auswertung Das Eis erwärmt sich nicht auf über 0°C, weil zuerst die Schmelzwärme überwunden werden muss. Außerdem wird die Außenschicht vom Eis permanent durch den Kern des Eiswürfels gekühlt. Der Kern hat nämlich eine Temperatur von maximal 0°C. Jetzt lesen wir die Werte für T A und T E aus dem Graphen ab und bestimmen m E : Wir stellen die Formel (4) um: m ⋅c W ⋅T A−T E −mE⋅c W⋅T E −T 0 q s= W W mE mW =120 g W =40 J K Jan Philip Nissen und Francis Wilken 27.11.2006 7 Spezifische Wärme von Metallen - Messwerte Durchführung 1 t /s T /° C t /s T /° C Jan Philip Nissen und Francis Wilken 27.11.2006 Durchführung 2 t /s T /° C t /s T /° C Jan Philip Nissen und Francis Wilken 27.11.2006 8 Spezifische Wärme von Metallen - Auswertung Jetzt lesen wir die Werte für T A und T m aus dem Graphen ab und bestimmen m M : Wir stellen die Formel (5) um: c ⋅m W ⋅T m−T A c M= W W m M⋅T M −T m mW =120 g W =40 J K