Berechnung eines Trapezwiderstandes

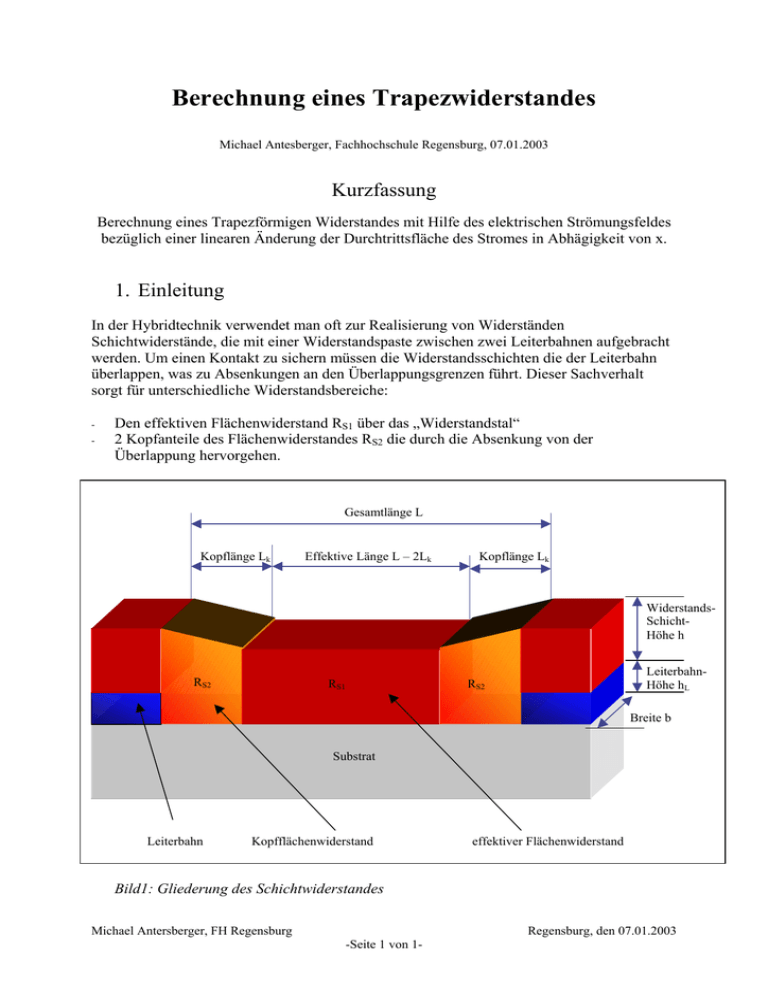
Berechnung eines Trapezwiderstandes
Michael Antesberger, Fachhochschule Regensburg, 07.01.2003
Kurzfassung
Berechnung eines Trapezförmigen Widerstandes mit Hilfe des elektrischen Strömungsfeldes
bezüglich einer linearen Änderung der Durchtrittsfläche des Stromes in Abhägigkeit von x.
1. Einleitung
In der Hybridtechnik verwendet man oft zur Realisierung von Widerständen
Schichtwiderstände, die mit einer Widerstandspaste zwischen zwei Leiterbahnen aufgebracht
werden. Um einen Kontakt zu sichern müssen die Widerstandsschichten die der Leiterbahn
überlappen, was zu Absenkungen an den Überlappungsgrenzen führt. Dieser Sachverhalt
sorgt für unterschiedliche Widerstandsbereiche:
-
Den effektiven Flächenwiderstand RS1 über das „Widerstandstal“
2 Kopfanteile des Flächenwiderstandes RS2 die durch die Absenkung von der
Überlappung hervorgehen.
Gesamtlänge L
Kopflänge Lk
Effektive Länge L – 2Lk
Kopflänge Lk
WiderstandsSchichtHöhe h
RS2
RS1
LeiterbahnHöhe hL
RS2
Breite b
Substrat
Leiterbahn
Kopfflächenwiderstand
effektiver Flächenwiderstand
Bild1: Gliederung des Schichtwiderstandes
Michael Antersberger, FH Regensburg
Regensburg, den 07.01.2003
-Seite 1 von 1-
• Der Gesamtwiderstand:
R =R
S1
⋅
L − 2 ⋅L
b
k + 2⋅R
L
⋅ k
S2 b
Hat man bereits mehrere Widerstände bemessen, die unterschiedliche Längen- und BreitenVerhältnisse aufweisen kann man durch die Anwendung der Linearen Regression den RS1 aus
der Steigung herauslesen. Dies geschieht mit folgender Formel einer Geradengleichung:
R ⋅ b = RS1 ⋅ L + 2 ⋅ (RS2 − RS1 ) ⋅ LK
y = m⋅ x
+
b
Die Kopfanteile RS2 kann man nur über eine Plausibilitätsbetrachtung vermuten. Unter der
Annahme eines an ein Trapez angenäherten Form des Kopfanteiles kann man bei Kenntnis
entsprechender Geometrieparameter diesen Flächenwiderstand in erster Annäherung
berechnen.
2. Hauptteil
In der obigen Abbildung (Bild1) sind die Kopfanteile des Flächenwiderstandes RS2 in
vereinfachter Annahme in Form eines Trapezes abgebildet. Es wird weiter vereinfacht
angenommen dass sich die Stromlinien und damit auch die Stromdichten homogen in diesem
Widerstandsblock verteilen. Die Durchtrittsfläche des Stromes ändert seinen Querschnitt A
linear, so dass man eine von x abhängige Querschnittsfläche A(x) bekommt:
A(x)
A1
I
A1
A2
I
A2
x
0
0
Lk
Lk
x
Bild2: Querschnittsfläche A(x)
Michael Antersberger, FH Regensburg
Regensburg, den 07.01.2003
-Seite 2 von 2-
• Formel für die in x-Richtung abhängige Querschnittsfläche A(x)
A( x ) = −
( A1 − A 2 )
( A − A1)
⋅ x + A1 = 2
⋅ x + A1
LK
LK
• Elektrisches Strömungsfeld
Unter der Annahme eines homogen im Trapez verteilten elektrischen Strömungsfeldes
kann man für die Stromdichte ebenfalls eine Abhängigkeit in x-Richtung feststellen:
j( x ) =
I
I
=
A( x ) ( A 2 − A1) ⋅ x + A
1
LK
• Elektrisches Feld
Im Zusammenhang der Stromdichte mit dem elektrischen Feld in Abhängigkeit von x
ergibt sich die nächste Formel:
E( x ) = ρ ⋅ j( x ) = ρ ⋅
I
( A 2 − A1)
⋅ x + A1
LK
• Spannungsabfall im Trapezwiderstand
Durch eine Integration der elektrischen Feldstärke mit den Integrationsgrenzen 0 nach Lk
bekommt man den Spannungsabfall über den Trapezwiderstand:


A 
1
Lk

 ⋅ dx = ρ ⋅ I ⋅
⋅ ln 2 
U = ∫ E( x ) ⋅dx = ρ ⋅ I ⋅ ∫
 ( A 2 − A1)

( A 2 − A1)  A1 
0
0
x + A1 

Lk


Lk

Lk 
Michael Antersberger, FH Regensburg
Regensburg, den 07.01.2003
-Seite 3 von 3-
• Trapezwiderstand
Der Widerstand der Trapezform berechnet sich durch die Division der anliegenden
Spannung durch den durchfließenden Strom:
R=
A 
U
Lk
= ρ⋅
⋅ ln 2 
( A 2 − A1)  A1 
I
Mit dieser Formel kann man nun in erster Näherung Trapezwiderstände berechnen. Für
unseren Spezialfall, der Berechnung des Flächenwiderstandes RS2 in einer
Hybridschaltung muss diese Formel entsprechend modifiziert werden.
• Definition des Flächenwiderstands Rq
R q= R ⋅
b
L
In unserem Fall ist es der Flächenwiderstand RS2 der aus dem Kopfwiderstand R2
hervorgeht.
RS2 = R 2 ⋅
b
Lk
• Definition des spezifischen Widerstands ρ
ρ = Rq ⋅h
In unserem Fall entnimmt man ρ aus dem schon bekannten Flächenwiderstandes RS11 mit
der Annahme eines gleichen ρ innerhalb der gesamten Widerstandspaste.
ρ = R S1 ⋅ h
• Der Flächenwiderstand RS2
RS2 =
A 
b
Lk
⋅ RS1 ⋅ h ⋅
⋅ ln 2 
Lk
( A 2 − A1)  A1 
1
Aus linearer Regression bekannt
Michael Antersberger, FH Regensburg
Regensburg, den 07.01.2003
-Seite 4 von 4-
• Definition der Flächen A1 und A2
Die beiden Flächen ergeben sich gemäß der beiden Abbildungen (Bild1 und Bild2) aus
Breite mal Höhe. Die Breite b ist bei beiden Flächen gleich. Die Höhe von A2 ist die der
Widerstandsschicht h, die Höhe von A1 ist die der Widerstandsschicht h addiert mit der
Höhe der der Leiterbahn hL. Die Flächen ergeben sich zu:
A1 = b ⋅ (h + hL )
A2 = b ⋅h
• Der Flächenwiderstand des Kopfanteils RS2
R
R

L
b
b ⋅ h 
k
⋅R ⋅h⋅
ln
S1
L
b ⋅ h − b ⋅ (h + h )  b ⋅ (h + h ) 
k
L 
L 
S2
=
S2
=−


S1 ⋅ ln h 
h+h 
h
L
L

h⋅R
3. Zusammenfassung
Zusammenfassend läst sich sagen, dass dies nur eine Abschätzung des RS2 ermöglicht. Mit
dieser Formel, der Formel aus der Plausibilitätsbetrachtung und den Ergebnissen aus der
Linearen Regression lässt sich auch die Länge des Kopfanteiles Lk abschätzen. Die
Schwierigkeiten Der Berechnung des RS2 besteht darin, dass das Strömungsfeld durch den
Kopfblock nicht homogen ist, und für diese Berechnung vereinfacht als homogen
angenommen wurde. Zusätzlich ist die Form des Kopfblockes mit einer Wölbung versehen,
die ebenfalls vereinfacht als linear abfallende Kante eines Trapezes angenommen wurde.
4. Literatur
[1]
[2]
Prof. Dr. Schiek, Script Grundlagen der Elektrotechnik 1b
Prof. Dr. Schlicht, Skript Praktikum Technologie Integrierter Schaltungen
Michael Antersberger, FH Regensburg
Regensburg, den 07.01.2003
-Seite 5 von 5-