Ts_phys3_2_ueaufg_sc..

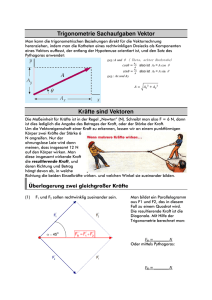
Fach: Physik/ L. Wenzl
|
Datum:
3.2.5 Zerlegung von Kräften (am Beispiel der schiefen Ebene)
Aus der Statik ist bekannt, dass sich resultierende Kräfte aus einzelnen Kräften zusammensetzen können
(Addition einzelner Kräfte).
Ebenso kann man umgekehrt eine angreifende Kraft in mehrere Komponenten (Teilkräfte) zerlegen.
(s. Buch S. 45, Kräfte an der geneigten Ebene)
Geneigte Ebene: z. B. Schlittenfahrt oder Schneelast, die auf Solarpanels liegt
FH
α
α
α
FG
FG
Am Schwerpunkt des Körpers greift die
Gewichtskraft FG an.
Sie ist der Auslöser, damit z. B. ein
Schlitten hangabwärts rutscht oder
dass eine Schneelast auf dem Dach (nicht)
abrutscht.
Je flacher der Winkel α ist, desto mehr
nähert man sich der waagr. Ebene.
der Körper rutscht dann nicht mehr.
Die Gewichtskraft FG teilt sich auf in
- eine Normalkraft FN und in eine
- eine Hangabtriebskraft FH
FN steht senkrecht auf der geneigten Ebene und
übt auf diese Druckkräfte aus.
Sie ist z. B. dafür verantwortlich, dass Schnee
nicht vom Dach rutscht
FH verläuft parallel zur geneigten Ebene und beschleunigt
Körper (z. B. Abrutschen von Schnee)
Der Winkel α, den die ebene mit der Waagrechten bildet, findet sich auch zwischen FG und FN wieder.
Mit diesem Winkel lassen sich die beiden Teilkräfte FN und FH berechnen.
FH = FG * sin α
Extremfälle: α ~ 0° (ganz flache Ebene) FN ~ FG; FH ~ 0 Es gibt keine Hangabtriebskraft (Flachdach)
Begründung: sin 0° = 0; cos 0° = 1
FN = FG * cos α
α
α ~ 90° (ganz steile Ebene) FN ~ 0; FH ~ FG Es gibt keine Normalkraft (Fassadenmontage)
Begründung: sin 90° = 1; cos 90° = 0
Übungsaufgabe: Auf einem Solarpanel (Fläche A ? 1,00 m2) liegt eine 0,400 m dicke Schicht Pappschnee mit der
Dichte 200 kg/m3. Das Panel ist mit einer Neigung von α = 30° gegenüber der Waagrechten
montiert.
a) Welche Masse hat der Schnee auf dem Panel und welche Gewichtskraft FG übt dieser
auf das Dach aus?
b) Welchen Betrag hat die Normalkraft FN, die auf das Panel drückt. Welche Flächenlast ergibt
sich für die PV Anlage?
c) Welche Hangabtriebskraft ergibt sich?
d) Welche Haftreibungszahl µo hat die Materialkombination Schnee-Glas, wenn der Schnee
gerade noch nicht abrutscht?
Fach: Physik/ L. Wenzl
|
Datum:
3.2.5 Zerlegung von Kräften (am Beispiel der schiefen Ebene)
Aus der Statik ist bekannt, dass sich resultierende Kräfte aus einzelnen Kräften zusammensetzen können
(Addition einzelner Kräfte).
Ebenso kann man umgekehrt eine angreifende Kraft in mehrere Komponenten (Teilkräfte) zerlegen.
(s. Buch S. 45, Kräfte an der geneigten Ebene)
Geneigte Ebene: z. B. Schlittenfahrt oder Schneelast, die auf Solarpanels liegt
FH
α
α
α
FG
FN
FG
Am Schwerpunkt des Körpers greift die
Gewichtskraft FG an.
Sie ist der Auslöser, damit z. B. ein
Schlitten hangabwärts rutscht oder
dass eine Schneelast auf dem Dach (nicht)
abrutscht.
Je flacher der Winkel α ist, desto mehr
nähert man sich der waagr. Ebene.
der Körper rutscht dann nicht mehr.
Die Gewichtskraft FG teilt sich auf in
- eine Normalkraft FN und in eine
- eine Hangabtriebskraft FH
FN steht senkrecht auf der geneigten Ebene und
übt auf diese Druckkräfte aus.
Sie ist z. B. dafür verantwortlich, dass Schnee
nicht vom Dach rutscht
FH verläuft parallel zur geneigten Ebene und beschleunigt
Körper (z. B. Abrutschen von Schnee)
Der Winkel α, den die ebene mit der Waagrechten bildet, findet sich auch zwischen FG und FN wieder.
Mit diesem Winkel lassen sich die beiden Teilkräfte FN und FH berechnen.
FH = FG * sin α
Extremfälle: α ~ 0° (ganz flache Ebene) FN ~ FG; FH ~ 0 Es gibt keine Hangabtriebskraft (Flachdach)
Begründung: sin 0° = 0; cos 0° = 1
FN = FG * cos α
α
α ~ 90° (ganz steile Ebene) FN ~ 0; FH ~ FG Es gibt keine Normalkraft (Fassadenmontage)
Begründung: sin 90° = 1; cos 90° = 0
Übungsaufgabe: Auf einem Solarpanel (Fläche A ? 1,00 m2) liegt eine 0,400 m dicke Schicht Pappschnee mit der
Dichte 200 kg/m3. Das Panel ist mit einer Neigung von α = 30° gegenüber der Waagrechten
montiert.
a) Welche Masse hat der Schnee auf dem Panel und welche Gewichtskraft FG übt dieser
auf das Dach aus?
b) Welchen Betrag hat die Normalkraft FN, die auf das Panel drückt. Welche Flächenlast ergibt
sich für die PV Anlage?
c) Welche Hangabtriebskraft ergibt sich?
d) Welche Haftreibungszahl µo hat die Materialkombination Schnee-Glas, wenn der Schnee
gerade noch nicht abrutscht?
Fach: Physik/ L. Wenzl
|
Datum:
3.2.6 Addition von Kräften
Bei Bewegungsvorgängen kommt es oft vor, dass verschiedene Kräfte am Bewegungsobjekt angreifen
(Bsp.: Ein Wagen erfährt eine beschl. Kraft FB, dieser wirkt aber eine verzögernde Reibungskraft FR entgegen)
Beispielaufgabe 1: (verschiedene Kräfte an der schiefen Ebene)
Anfahren am Berg = Beschleunigungsvorgang an der geneigten Ebene
Ein Pkw (m=1,20 t) fährt nach einer Bremsung am Chamer Schulberg (α =33,0°) wieder aus dem
Stillstand an. Er beschleunigt in 5,00 s auf v = 36,0 km/h. Als Rollreibung verwenden Sie
Gummi auf Teer (µr = 0,0500)
a) Geben Sie alle Kräfte an, die einen direkten Einfluss auf den Beschleunigungsvorgang des
Wagens haben! Zeichnen Sie diese in die Skizze ein! (FG ist z. B. nur indirekt beteiligt, weglassen)
Es wirken:
- ______________________________
- ______________________________
α
- ______________________________
Berechnen Sie die einzelnen Kräfte und bestimmten Sie daraus die Gesamtkraft FM,
die vom Motor für diesen Bewegungsvorgang aufzubringen ist.
Geg.:
Ges.:
FH
Beispielaufgabe 2: (Zugkräfte am Seil)
Ein Kran soll eine Palette Ziegel (m=1,00 t) so anheben, dass diese in 3,00 s die Geschwindigkeit v = 3,00 m/s erreicht. Welche Kräfte wirken, wie groß ist die Gesamtkraft Fges
während und nach dem Beschleungigungsvorgang?
Geg.:
Ges.:
Es wirken: _____________________________ + ______________________________
Warum reissen Abschleppseile besonders „gerne“ beim Anfahren?
Fach: Physik/ L. Wenzl
|
Datum:
3.2.6 Addition von Kräften
Bei Bewegungsvorgängen kommt es oft vor, dass verschiedene Kräfte am Bewegungsobjekt angreifen
(Bsp.: Ein Wagen erfährt eine beschl. Kraft FB, dieser wirkt aber eine verzögernde Reibungskraft FR entgegen)
Beispielaufgabe 1: (verschiedene Kräfte an der schiefen Ebene)
Anfahren am Berg = Beschleunigungsvorgang an der geneigten Ebene
Ein Pkw (m=1,20 t) fährt nach einer Bremsung am Chamer Schulberg (α =33,0°) wieder aus dem
Stillstand an. Er beschleunigt in 5,00 s auf v = 36,0 km/h. Als Rollreibung verwenden Sie
Gummi auf Teer (µr = 0,0500)
a) Geben Sie alle Kräfte an, die einen direkten Einfluss auf den Beschleunigungsvorgang des
Wagens haben! Zeichnen Sie diese in die Skizze ein! (FG ist z. B. nur indirekt beteiligt, weglassen)
Es wirken:
FB
- beschleunigende Kraft FB
- Reibungskraft FR
FR
FH
α
- Hangabtriebskraft FH
Berechnen Sie die einzelnen Kräfte und bestimmten Sie daraus die Gesamtkraft FM,
die vom Motor für diesen Bewegungsvorgang aufzubringen ist.
Geg.:
Ges.:
FH
Beispielaufgabe 2: (Zugkräfte am Seil)
Ein Kran soll eine Palette Ziegel (m=1,00 t) so anheben, dass diese in 3,00 s die Geschwindigkeit v = 3,00 m/s erreicht. Welche Kräfte wirken, wie groß ist die Gesamtkraft Fges
während und nach dem Beschleungigungsvorgang?
Geg.:
Ges.:
Warum reissen Abschleppseile besonders „gerne“ beim Anfahren?