Feder-Schwere-Pendel - mathphys

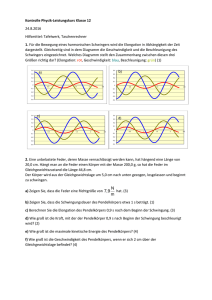
mathphys-online
Das Feder-Schwere-Pendel
Theorie
Am unteren Ende einer vertikal aufgehängten Feder mit der Federkonstanten D wird ein Körper
befestigt, dessen Masse m so groß ist, dass die Masse der Feder vernachlässigt werden kann.
Der Körper und die Schraubenfeder bilden zusammen ein Feder-Schwere-Pendel.


Durch die Gewichtskraft FG des Pendelkörpers wird die Feder um Δy vorgedehnt (siehe die in


der Skizze eingezeichnete Vordehnung Δy).
Wird das Pendel in vertikaler Richtung
ausgelenkt und dann losgelassen, so
schwingt der Pendelkörper längs einer
vertikalen Achse auf und ab.
Für die bei der Schwingung auftretenden Dehnungen der Feder gilt
das Hookesche Gesetz. Dämpfungsverluste sind vernachlässigbar klein.

Zum Nachweis, dass das System harmonisch schwingt, wird für die rücktreibende Kraft Frück ein
lineares Kraftgesetz nachgewiesen.
___________________________
Das Feder-Schwere-Pendel
Seite 1 von 3
mathphys-online
Gleichgewichtslage:
FG = FF
m  g = D  Δy
⇔


Frück = FF  FG = D  Δy  y0  m  g
Rücktreibende Kraft:
Frück = D  Δy  D  y0  D  Δy
Frück = D  y0



Frück und y0 haben entgegengesetztes Vorzeichen:



Frück = D  y0
lineares Kraftgesetz, also harmonische Schwingung.
Bemerkung: Die Schwingung ist unabhängig von der Vorspannung.
Bei einer harmonschen Schwingung gilt für die Bewegungsgleichung:
y ( t) = y0  sin ( ω  t  φ)
Befindet sich der Massenschwerpunkt zum Zeitpunkt t0 = 0  s im oberen Umkehrpunkt, so gilt:
Momentane Elongation:
y ( t) = y0  cos ( ω  t)
Geschwindigkeit:
v ( t) =
d
dt
Beschleunigung:
a ( t) =
d
( s ( t) ) = y0  ω  sin ( ω  t) = v0  sin ( ω  t)
d
v ( t) =
2
dt
⇒
2
dt
2
y ( t) = y0  ω  cos ( ω  t) = a0  cos ( ω  t)
2
a ( t) = ω  s ( t)
Beispiel
Gegeben ist das Feder-Schwere-Pendel der Masse m 1  1  kg , die Federkonstante beträgt
N
D  2  .
m
a) Berechnen Sie die Schwingungsdauer T.
b) Stellen Sie das schwingende System und die Bewegungsgleichungen graphisch dar.
Teilaufgabe a)
Schwingungsdauer: T  2  π 
___________________________
Das Feder-Schwere-Pendel
Seite 2 von 3
m1
D
T  4.443 s
mathphys-online
Darstellung und Animation
Weg, Geschwindigkeit und Beschleunigung
0.4
T
2 T
rot: Elongation
blau: Geschwindigkeit
grün: Beschleunigung
0.3
0.2
ymax
0.1
0
10
20
 0.1
 ymax
 0.2
 0.3
Zeit t
Elongation:
2
t  27 s
Elongation:
Geschwindigkeit:
Beschleunigung:
y  0.11 m
m
vK  0.08
s
m
aK  0.21
2
s
___________________________
Das Feder-Schwere-Pendel
Seite 3 von 3
30