1 Tabellen Angenommen, wir wollen eine Datenbank
Werbung
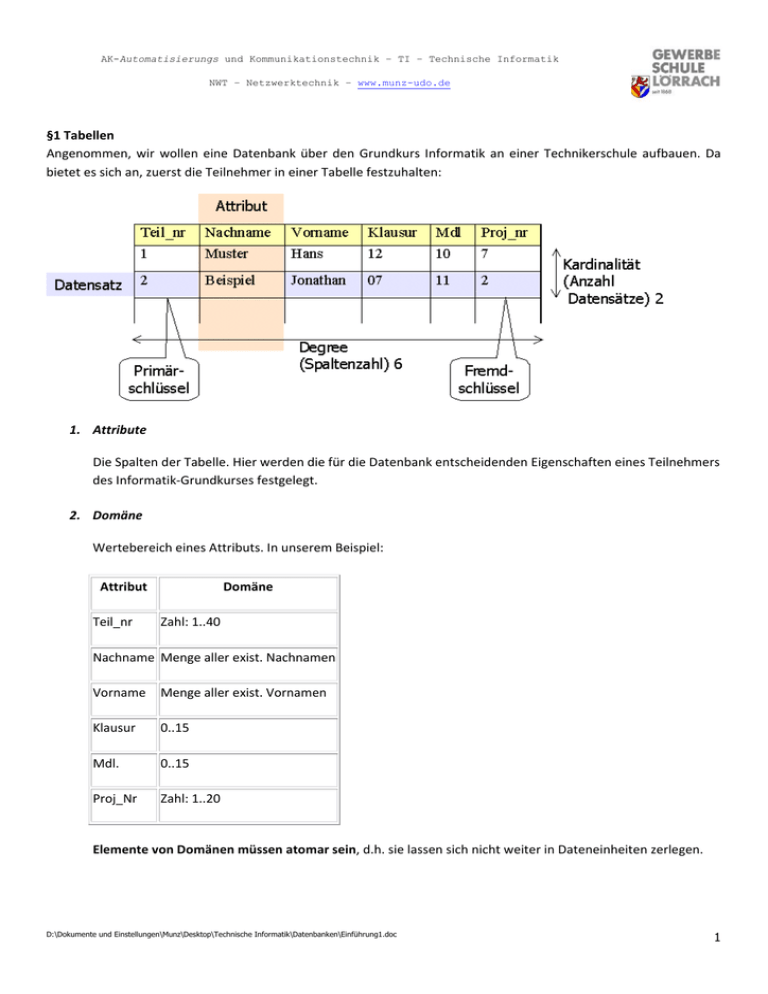
AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de §1 Tabellen Angenommen, wir wollen eine Datenbank über den Grundkurs Informatik an einer Technikerschule aufbauen. Da bietet es sich an, zuerst die Teilnehmer in einer Tabelle festzuhalten: 1. Attribute Die Spalten der Tabelle. Hier werden die für die Datenbank entscheidenden Eigenschaften eines Teilnehmers des Informatik‐Grundkurses festgelegt. 2. Domäne Wertebereich eines Attributs. In unserem Beispiel: Attribut Teil_nr Domäne Zahl: 1..40 Nachname Menge aller exist. Nachnamen Vorname Menge aller exist. Vornamen Klausur 0..15 Mdl. 0..15 Proj_Nr Zahl: 1..20 Elemente von Domänen müssen atomar sein, d.h. sie lassen sich nicht weiter in Dateneinheiten zerlegen. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 1 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Beispiel 1: Eine Adresse ist nicht atomar, denn sie lässt sich in Ort, Postleitzahl, Straße und Hausnummer zerlegen. Beispiel 2: Eine Zahl ist atomar. Zwei verschiedene Attribute können zur gleichen Domäne gehören. (In unserem Beispiel „Klausur" und „Mdl" ) 3. Datensätze Zeilen der Tabelle. Die Zahl der Zeilen entspricht der Zahl der Teilnehmer des Grundkurses. Jeder Schüler entspricht einem Datensatz in der Tabelle. Eine Tabelle muss eindeutig sein, d.h. kein Schüler darf mehr als einmal vorkommen (mathematischer: keine zwei Zeilen dürfen identisch sein!). 4. Bedingungen an eine Tabelle Eindeutigkeit Zu keinem Zeitpunkt existieren zwei identische Datensätze in der Tabelle. atomare Attribute Eine Tabelle einer Datenbank besitzt ausschließlich atomare Domänen, bzw. Attribute. Sortierung Die Datensätze sind zu jedem Zeitpunkt als unsortiert anzusehen Reihenfolge der Attribute Auch die Attributreihenfolge ist zu keinem Zeitpunkt fest definiert. Die letzten zwei Bedingungen lassen keinen Zugriff über einen Index zu, z.B. "Wie lautet der Wert des 4. Attributs in der 3. Zeile". Zugriffe erfolgen nur über die zugehörigen "Schlüsselwörter", z.B. "Wie lautet der Wert des Attributs "Klausur" im Datensatz "Muster" ? D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 2 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 5. Operationen auf Tabellen Folgende Operationen sind auf Tabellen definiert: (leeren) Datensatz hinzufügen Daten(satz) suchen Datenfelder ändern Datensatz löschen (Attribute hinzufügen/löschen) Der letzte Punkt wird nur von einigen Datenbanksystemen erlaubt. §2 Modelle Um eine möglichst sinnvolle Beschreibung des Informatikgrundkurses in einer Datenbank unterzubringen, stellt sich die Frage was für Informationen wie gespeichert werden sollen. Dabei macht man sich ein Abbild von der "Wirklichkeit", ein "Modell". Was ist ein Modell? Heinrich Hertz (Ende 19. Jahrhundert) "Wir machen uns innere Scheinbilder oder Symbole der äußeren Gegenstände, und zwar machen wir sie von solcher Art, dass die denknotwendigen Folgen der Bilder stets wieder Bilder seien von den Folgen der abgebildeten Gegenstände." Prinzip der Modellbildung Der beobachtete Sachverhalt kann durch ein Modell nicht in seiner Gesamtheit erfasst werden. Dies wird in der Zeichnung durch eine "Projektion" angedeutet: Es findet ein Verlust an Information statt, das "Bild" des Sachverhalts ist nur noch zweidimensional. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 3 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Deshalb wird ein Projekt unter einem bestimmten "Aspekt" erstellt, es ist dann umso "brauchbarer" je eher sich der tatsächliche Sachverhalt mit dem Modell simulieren lässt. Î s. Jeckle UML‐Modell Beispiele für Modelle Reiz‐ Reaktionsreflex (Psychologie) Der russische Psychologe Iwan Petrowitsch Pawlow erhielt 1904 für seine Untersuchung des Speichelflussreflexes bei Hunden den Nobelpreis. Normalerweise müsste bei einem Hund der Speichelfluss ausgelöst werden, wenn er Kontakt mit der Nahrung aufgenommen hat. Pawlow konnte aber nachweisen, dass der Speichelfluss des Hundes bei regelmäßiger Fütterung bereits mit Erscheinen des Wärters stattfand. In weiteren Versuchen konnte er sogar den Speichelfluss durch unterschiedliche Reize, wie zum Beispiel dem Ertönen einer Klingel auslösen. Daraus leitete er das folgende "Lernmodell" ab (Reiz‐Reaktions‐Lernen oder klassisches Konditionieren). Schema des Reiz‐Reaktionslernens Das Modell vom Massenpunkt (Physik) In der Physik der 11. Klasse (Mechanik) werden verschiedene Bewegungen beschrieben: Horizontaler und schiefer Wurf, Kreisbewegung, Bewegungen bei linearem Kraftgesetz usw. Die Beschreibung erfolgt durch Angabe von x‐ und y‐ Koordinate des Körpers in der Zeit. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 4 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Aber werfen Sie einmal einen Bumerang. Wo (am Bumerang) befindet sich diese x‐ und y‐ Koordinate? Wurf eines Bumerangs Die Antwort scheint klar: Die (berechnete) Wurfparabel beschreibt die Bahn des Schwerpunkts. Ist dann der Wurf auf diese Weise vollständig beschrieben? Angenommen der Bumerang fliegt nah einem Baum vorbei (dessen x‐ und y‐ Koordinaten auch bekannt sind). Wann wird der Baum getroffen? Oder betrachten wir die für die "Rückkehr" so wichtige Drehung des Wurfgeschosses: Wird sie bei der Bahnbeschreibung mitberücksichtigt? All diese Fragen entstehen, weil man dem Modell von der Bahnbeschreibung zuviel zumutet; es handelt sich lediglich um die Beschreibung der Bewegung eines Massenpunktes, in dem man sich die gesamte Masse des Objektes konzentriert denkt. Ein typisches Problem bei der Modellierung ist die Verwechslung des Modells mit der Wirklichkeit. Das kann zu scheinbaren Paradoxien führen. Scheinbare Paradoxien In der Physik lässt sich das Verhalten von Elektronen unter bestimmten Bedingungen mit dem Verhalten eines "Teilchens" erklären, unter bestimmten Bedingungen aber nur mit dem Verhalten einer "Welle". Vergisst man, dass man sich nur ein Modell vom Elektron gemacht hat, so widerspricht sich dieses Verhalten: Ö Quantenphysik Ö Psychologie = Die Kunst der Wahrnehmung D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 5 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Zylinderparadoxon Erst mit der Existenz des Elektrons als "Quantenobjekt" (das sich der bildhaften Vorstellung entzieht) lässt sich dieser scheinbare Widerspruch aufklären. Achilles und die Schildkröte (Grenzwerte – Limes – Mathematik) Achilles und die Schildkröte laufen um die Wette. Da Achilles schneller ist, gibt er der Schildkröte einen Vorsprung. Wettlauf Betrachten wir den Lauf aus folgender Sicht: In der Zeit, in der Achilles den Vorsprung der Schildkröte gelaufen ist, hat die Schildkröte selbst einen bestimmten Weg zurückgelegt; jetzt befindet sich Achilles an ihrer alten Position, die Schildkröte hat aber nach wie vor wieder einen Vorsprung. Ab hier lässt sich dieses Spiel unendlich oft wiederholen. Also wird Achilles die Schildkröte niemals einholen! Welcher Fehler wurde hier bei der Modellbildung gemacht? Der Ansatz ist vollkommen in Ordnung, nur spielt uns hier unsere Erfahrung einen Streich. Achilles holt die Schildkröte ein, wenn sich der Vorgang unendlich oft wiederholt hat, das ist aber trotzdem ein endliches Zeitintervall. Beispiel: Wenn man zu einer Zahl unendlich oft die Hälfte und die Hälfte ihrer Hälfte, usw. addiert, so erhält man (nach unendlichem Wiederholen) nur das Doppelte: D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 6 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Unendliche Summe mit endlichem Ergebnis Es ist also immer zu testen, ob Erfahrungseindrücke und Assoziatonen, die mit der Modellbildung verbunden sind, den Modellannahmen widersprechen, oder ihnen gerecht werden. Oder mit den Worten aus einem Physikbuch: "Modelle sind also Vorstellungshilfen und Wirklichkeitshilfen, nicht die Wirklichkeit selbst." (Metzler Physik). §3 Das Entitiy‐Relationship‐Modell Ziel der folgenden Kapitel ist es, Daten eines realen Systems in die Tabellenstruktur einer Datenbank zu transformieren. Dazu benutzt man das sogenannte "Entity‐Relationship‐Modell". Durch Festlegung aller, für den Grundkurs relevanten Attribute erhält man eine große Menge an Daten, die zuerst einmal völlig unstrukturiert sind. Beispielsweise Projektdaten, Personendaten, Noten, Lehrer, ... usw. Um eine Struktur der Daten zu erfassen, ist es notwendig, ihre Beziehungen zu erfassen. Dazu versucht man, Attribute bestimmten "Entities" zuzuordnen, deren Beziehungen dann geklärt werden müssen. Entity‐Relationship‐Diagramme Entities werden hier durch rechtecke Symbole dargestellt: Eine Entität (entity) ist ein individuelles Exemplar von Elementen der realen oder der Vorstellungswelt. Um die Struktur unter den Enitities zu klarzumachen, werden sie mit Linien verbunden, die den Bezug kennzeichnen. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 7 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Beziehungsgrad Schauen wir uns folgende Beziehung genauer an: Man unterscheidet drei verschiedene Beziehungsgrade: • • • 1:1 1:N N:M Eins‐zu‐Eins‐Beziehung Eins‐zu‐viele‐Beziehung Viele‐zu‐viele‐Beziehung 1:1‐Beziehung Genau ein Schüler erarbeitet genau einen (oder keinen) CD‐ROM‐Beitrag oder umgekehrt jeder Beitrag wird auch genau von einem (oder keinem) Schüler erzeugt. Man könnte auch sagen: Bei einer 1:1 Beziehung wird jedem Datensatz von Entity A nicht mehr als ein Datensatz der Entity B zugeordnet und umgekehrt. 1:N‐Beziehung Ein Schüler kann keinen, einen oder mehrere Beiträge zur CD‐ROM liefern. Allerdings muss jeder Beitrag von einem (oder keinem) Schüler kommen. N:M‐Beziehung Ein Schüler kann keinen, einen oder mehrere Beiträge liefern und jeder Beitrag kann von keinem, einem oder mehereren Schülern erstellt worden sein. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 8 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Beziehungen im Informatik‐Grundkurs Aus den alltägliche Erfahrungen gilt wohl der folgende Zusammenhang: Dieses Diagramm gibt die Beziehungen zwischen Schülern und Projekten und zwischen Schülern und CD‐ROM‐ Beiträgen schon ganz gut wieder. Obligatorische Mitgliedschaft Jetzt ist noch der Fall erlaubt, dass ein Schüler kein Projekt hat. Dieser Fall darf aber in der Realität nicht möglich sein. Deshalb kann man im ER‐Modell auch sogenannte "obligatorische Mitgliedschaften" definieren: Ein Schüler muss genau ein Projekt bearbeiten, während ein Projekt nach wie vor von keinem, einem oder mehreren Schülern bearbeitet werden kann. Die obligatorische Mitgliedschaft schließt bei der Entity den Fall aus, dass ein Datensatz nicht an der Beziehung teilnimmt. §4 Ein einfaches Beispiel Im Folgenden wird versucht, ein Modell der wichtigsten Daten des Grundkurses Informatik zu entwickeln und daraus eine Datenbank zu erstellen. Entities des Grundkurses Informatik Bei einer Sammlung von Daten‐Hauptgruppen kommt man vielleicht auf folgende Skizze: http://beat.doebe.li/bibliothek/w00887.html http://www.topic‐maps.at/ Î semantische Netze Î AI D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 9 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Nun werden die einzelnen "Entities" über Beziehungen miteinander verbunden. Der Text weist dabei vom Subjekt zum Objekt. Jetzt fehlen nur noch die (für die Datenbank wichtigen) Arten der Relationen. • • • • • Während ein Team N Teilnehmer haben kann, hat ein Teilnehmer genau ein Team: 1 : N (obligatorisch) Jeder Teilnehmer schreibt genau eine Klausur: 1:1 (obligatorisch) Jedes Team arbeitet an genau einem Projekt: 1:1 (obligatorisch) Ein Projekt ist Thema von N Sitzungen, eine Sitzung handelt von genau einem Projekt: 1:N (obligatorisch) Jeder Teilnehmer muss in eine oder mehrere Sitzungen, in jeder Sitzung befinden sich einer oder mehrere Teilnehmer: N:M (obligatorisch) D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 10 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Daraus ergibt sich nun folgendes Diagramm: Ein ER‐Modell des Grundkurses Informatik Einige Anmerkungen zum Modell: Natürlich sind nicht alle Beziehungen eingezeichnet; man wird sich im jeweiligen Fall überlegen, ob man weitere Verbindungen hinzufügt. Interessant sind hier auch "Doppelwege": Die Sitzung hat eine direkte Beziehung zum Teilnehmer (N:M) und eine indirekte über "Projekte" und "Teams". Das macht in diesem Fall sogar einen Sinn. In der direkten Verbindung kann man die tatsächlich in einer Sitzung anwesenden Teilnehmer eines Teams sehen (gut für die Beurteilung durch den Lehrer), während der Umweg über die Projekte und die Teams immer alle Teammitglieder einer Sitzung zuordnet. Ideen zur Umwandlung in das Tabellenmodell Ziel der Modellierung ist es, die Daten möglichst einfach und sinnvoll in verschiedenen Tabellen der Datenbank zu speichern (wobei die Tabellen selbst natürlich auch ein Modell der Realität sind). Dabei ist das ER‐Diagramm bereits eine große Hilfe. In einem ersten Ansatz wird man z.B. jede Entität mit einer Tabelle in Verbindung bringen: • • • • • Tabelle Teilnehmer: Enthält alle für den Grundkurs wichtigen Angaben zu den Teilnehmern (also Name und Vorname) Tabelle Klausuren: Kann die einzelnen Punkte der Aufgaben und die Endnote speichern. Tabelle Teams: Enthält die Nummer der jeweiligen Teilnehmer. Tabelle Projekte: Enthält Projektnamen und evtl. Projektstand, Aufgabenstellung, Termine etc... Tabelle Sitzungen: Enthält die Protokolle mit den jeweilig erreichten und gesetzten Zielen. Eine "Kopplung" von Tabellen fordert im Datenbanksystem evtl. Mehraufwand. Deshalb kann man sich überlegen, ob man bestimmte Entitäten mit 1:1 Relationen in eine Tabelle zusammenfasst: Teams Projekte 1 : 1 Projektname Beschreibung Name 1 Name 2 Name 3 D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 11 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de wird also zu einer Tabelle: Projekte Projektname Beschreibung Name 1 Name 2 Name 3 Die 1:1 Relation zwischen Teilnehmer und Klausuren würde dann so ausschauen: Teilnehmer Name Vorname Punkte für Aufgabe 1 Punkte für Aufgabe 2 Punkte für Aufgabe 3 Klausurnote §5 Tabellenmodell des Grundkurses Informatik Aus den Angaben der vorhergehenden Kapitel entsteht nun ein Datenbankmodell mit den einzelnen Tabellen. Umsetzung der Entitäten Aus dem ER‐Modell und der Verbindung von 1:1‐Relationen entstehen nun folgende Tabellen: Teilnehmer Name Vorname Punkte für Aufgabe 1 Punkte für Aufgabe 2 Punkte für Aufgabe 3 Punkte für Aufgabe 4 Klausurnote Mündliche Note Projekte Projektname Beschreibung Teilnehmer 1 Teilnehmer 2 Teilnehmer 3 Sitzungen Datum Projektname Erreichte Ziele Angestrebte Ziele D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 12 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Umsetzung der Relationen Um die Relation (1:N) zwischen Sitzungen und Projekten aufzulösen, muss man die zugehörige Information mit im Datenbanksystem speichern. Man braucht also entweder in der Tabelle "Projekte" oder in der Tabelle "Sitzungen" ein zusätzliches Attribut für die Zuordnung. Würde diese Information bei "Projekte" mitgespeichert, so ergäben sich Mehrfachzuordnungen (ein Projekt hat mehrere Sitzungen). Wegen der 1:N Beziehung klappt aber der umgekehrte Fall: Zu jeder Sitzung wird die Nummer des Projektes gespeichert. Dies setzt voraus, dass sich jedes Projekt eindeutig über eine Nummer ansprechen lässt. Wie aber in § 1 gezeigt, darf man nicht annehmen, dass der gleiche Datensatz immer in der gleichen Zeile liegt. Deshalb muss für die Projekte ein zusätzliches Attribut mit einer Identifikationsnummer ("ID") definiert werden, deren Inhalt eindeutig ist. Solche Attribute eignen sich gut als Primärschlüssel und werden nach ihrer Definition von der Datenbank eigenständig verwaltet. Es ergeben sich folgende neue Tabellen: Projekte ID Projektname Beschreibung Teilnehmer 1 Teilnehmer 2 Teilnehmer 3 Sitzungen Datum Projektnummer (‐»Projekt.ID) Erreichte Ziele Angestrebte Ziele Durch diesen "Trick" wurde gleichzeitig vermieden, dass man bei der Sitzung einen anderen Projektnamen einträgt, als tatsächlich vorhanden ist. Da die Zuordnung eindeutig ist, kann man jederzeit den Namen des Projektes in der Sitzung weiterverwenden. Eine weitere Relation ist auch noch nicht optimal gelöst: Die Beziehung zwischen Projekten und Teilnehmern. In der obigen Struktur werden die Namen der Teilnehmer im Projekt eingetragen. Auch hier ist sozusagen ein Name in der Datenbank doppelt vorhanden (In "Projekt" einmal und in "Teilnehmer" einmal) und kann zu Fehlern führen. Betrachten wir uns die Relation genauer: In einem Projekt können sich mehrere Teilnehmer befinden, jeder arbeitet aber an genau einem Projekt. (1:N) Auch hier ist es am einfachsten, die eindeutige Projektnummer beim Teilnehmer zu speichern und dafür die Namen der Teilnehmer aus der Projekttabelle zu entfernen. Nebenbei ist es nun auch möglich, Projekte mit mehr oder weniger als drei Teilnehmern zu starten. Jetzt bleibt nur noch die Beziehung zwischen den Teilnehmern und den Sitzungen aufzulösen. Wie schon erwähnt, soll hier mitgeführt werden, welche Teilnehmer eines Projekts in der Sitzung anwesend waren. Da es sich hier um eine N:M ‐ Relation handelt lässt sie sich weder bei den Sitzungen (mehrere Teilnehmer pro Sitzung) noch bei den Teilnehmern (mehrere Sitzungen pro Teilnehmer) speichern. Deshalb müssen Teilnehmer und Sitzungen ebenfalls eindeutig identifizierbar werden und es wird eine eigene Tabelle für diese Zuordnung eingeführt: D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 13 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Teilnehmer ID Name Vorname Punkte für Punkte für Punkte für Punkte für Mündliche Projektnummer (‐ Klausurnote Aufgabe 1 Aufgabe 2 Aufgabe 3 Aufgabe 4 Note »Projekt.ID) Sitzungen ID Datum Projektnummer (‐»Projekt.ID) Erreichte Ziele Angestrebte Ziele Anwesenheit Teilnehmernr. (‐»Teilnehmer ID) Sitzungsnr. (‐»Sitzung ID) Hier nun das vorläufig fertige Tabellenmodell: Das Tabellenmodell Teilnehmer Punkte Punkte Punkte Punkte Mündliche Projektnummer ID Name Vorname für für für für Klausurnote Note (‐»Projekt.ID) Aufgabe 1 Aufgabe 2 Aufgabe 3 Aufgabe 4 Projekte Projektname Beschreibung Sitzungen ID Datum Projektnummer (‐»Projekt.ID) Erreichte Ziele Angestrebte Ziele D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 14 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Anwesenheit Teilnehmernr. (‐»Teilnehmer ID) Sitzungsnr. (‐»Sitzung ID) Aufgaben zum Thema Datenbanken 1. Zählen Sie Attribute und Domänen für Tabellen auf, die folgendes speichern: a) Adressen b) CDs c) Schriftliche und mündliche Noten aller Grundkurse 2. Welche Bedingungen werden an eine Tabelle gestellt? 3. Welche Operationen sind auf einer Tabelle definiert? 4. Erklären Sie anhand eines Beispiels, was man unter einem "Modell" versteht. 5. Ein Modell stellt immer eine Projektion der "Wirklichkeit" dar. Erklären Sie diesen Sachverhalt am Beispiel des "Zylinderparadoxons". 6. Eine "Modelleisenbahn" ist das Modell einer wirklichen Eisenbahn. Belegen Sie diese Aussage anhand eines Beispiels und zeigen Sie Grenzen dieses Modells auf. 7. Skizzieren Sie jeweils ein ER‐Modell für Datenbanken, die folgende Daten speichern: a) Lehrer, Klassen und Schüler einer Schule (ohne Noten) b) Artikel, Lieferscheine und Kunden einer Firma 8. Versuchen Sie, die folgenden ER‐Modelle in Tabellen einer Datenbankanwendung umzusetzen: D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 15 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de a) b) Lösungen 1. Zählen Sie Attribute und Domänen für Tabellen auf, die folgendes speichern: a) Adressen b) CDs c) Schriftliche und mündliche Noten aller Grundkurse 1a) Im Allgemeinen speichert man bei Adressen Name, Vorname, Postleitzahl, Ort, Straße und Telefonnummer. Domänen sind hier alle Namen, alle Vornamen, alle Postleitzahlen, alle Orte, alle Straßennamen und alle Telefonnummern. 1b) Eine CD‐Sammlung wird etwa den Titel, den Interpreten, das Veröffentlichungsjahr und die Länge speichern. Domänen sind alle Title, alle Interpreten, 1960..2001 (Jahr) und 0..160 (Minuten). 1c) Jeder Grundkurs findet in einem Fach statt, hat eine Bezeichnung und einen Lehrer. Es wird eine Klausurnote geben und vielleicht drei mündliche Noten. Die Fachbezeichnung stammt aus einer der Domäne aller Kollegstufenfächer, die Kurzbezeichnung aus der aller Grundkurskürzel, der Lehrer aus der Menge aller Lehrernamen, die Klausurnote und die mündlichen Noten aus 0..15. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 16 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 2. Welche Bedingungen werden an eine Tabelle gestellt? Die Bedinungen sind: • • • • Eindeutigkeit: Zu keinem Zeitpunkt existieren zwei identische Datensätze in der Tabelle. Atomare Attribute: Eine Tabelle einer Datenbank besitzt ausschließlich atomare Domänen, bzw. Attribute. Sortierung: Die Datensätze sind zu jedem Zeitpunkt als unsortiert anzusehen Reihenfolge der Attribute: Auch die Attributreihenfolge ist zu keinem Zeitpunkt fest definiert. 3. Welche Operationen sind auf einer Tabelle definiert? Die Operationen sind: • • • • • (leeren) Datensatz hinzufügen Daten(satz) suchen Datenfelder ändern Datensatz löschen (Attribute hinzufügen/löschen) 4. Erklären Sie anhand eines Beispiels, was man unter einem "Modell" versteht. Ein Modell ist eine "Projektion" der Wirklichkeit. Bei einem guten Modell lassen sich Schlüsse in der Projektion unter bestimmten Bedingungen auf die Realität zurückübertragen. Da man sich aber nur in einem "Abbild" befindet, kann eine Schlussfolgerung auch zu falschen Aussagen führen, die mit dem Verhalten der Realität dann nicht mehr übereinstimmen. Monopoly zeigt wesentliche Prinzipien des Mietens, Erwerbens und Handelns von Immobilien. Aus ein paar Grundgegebenheiten (Existenz von "Geld", Spielfeld) ergeben sich mit einem einfachen Regelwerk Spielsituationen, die der Realität schon ziemlich nah kommen. (Um z.B. bestimmte Immobilien zu erwerben, kann man sich bei einem Mitspieler zu "Wucherzinsen" etwas ausborgen) 5. Ein Modell stellt immer eine Projektion der "Wirklichkeit" dar. Erklären Sie diesen Sachverhalt am Beispiel des "Zylinderparadoxons". Die Projektion eines Zylinders kann einen Kreis oder ein Rechteck ergeben. Beide "Schatten" stammen vom gleichen Objekt. Ist es nun ein Rechteck oder ein Kreis? Dieser scheinbare Widerspruch löst sich erst, wenn man die Projektion (das Modell) nicht mit dem Objekt (der Realität) gleichsetzt und akzeptiert, dass man bei der Projektion (Modellierung) Information verliert. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 17 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 6. Eine "Modelleisenbahn" ist das Modell einer wirklichen Eisenbahn. Belegen Sie diese Aussage anhand eines Beispiels und zeigen Sie Grenzen dieses Modells auf. Eine Modelleisenbahn hat viel von der Funktionalität einer echten Eisenbahn. Es können Weichen und Signale gestellt werden, es können Wagen an‐ und abgekuppelt werden, es gibt unterschiedliche Lokomotiven, Bahnhöfe und freie Strecken usw... Die Grenzen des Modells liegen dort, wo die Funktion des Modells nicht gebraucht wird. Wenn sich zum Beispiel in der Kulisse Menschen und Autos befinden, so bewegen sie sich im allgemeinen nicht. (Das tut dem "Spielspaß" normalerweise keinen Abbruch, denn es geht ja darum, Züge zu bewegen). Häufig werden bei Modellbahnen auch die Kurvenradien deutlich enger sein als es nach dem Maßstab möglich ist. Dies liegt daran, dass man nicht beliebig viel Platz für das Modell zur Verfügung hat. Wegen der engeren Kurvenradien haben die einzelnen Wagen einen größeren Abstand gegnüber einem maßstabsgetreuen Original. 7. Skizzieren Sie jeweils ein ER‐Modell für Datenbanken, die folgende Daten speichern: a) Lehrer, Klassen und Schüler einer Schule (ohne Noten) b) Artikel, Lieferscheine und Kunden einer Firma a) b) D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 18 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de 8. Versuchen Sie, die folgenden ER‐Modelle in Tabellen einer Datenbankanwendung umzusetzen: a) b) a) Im ersten Fall haben wir eine 1:1 Beziehung; die läßt sich in einer Tabelle auflösen. Lehrer Name Vorname Straße Postleitzahl Ort b) Wir brauchen sowohl für die CD einen "Foreign‐Key" , der den Interpreten speichert, als auch bei den Songs einen "Foreign‐Key", der die zugehörige CD speichert. Das ganze schaut dann etwa so aus: D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 19 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Songs ID Name Zeit CD* CDs ID Titel Zeit Interpret* Interpreten ID Name Vorname Haargel ... Die "Sternchen"‐Attribute sind jeweils die "Foreign‐Keys". D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 20 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de §6 Anforderungen an eine Datenbank Die folgenden Anforderungen sind optional. Je mehr von ihnen erfüllt sind, desto weniger Fehler können im laufenden Betrieb gemacht werden. Rererentielle Integrität Wie im letzten Kapitel gezeigt, werden 1:N Relationen über einen "Foreign Key" (Zeiger in eine andere Tabelle) und einen "Primary Key" (Primärschlüssel) in der anderen Tabelle aufgelöst. "Referentielle Integrität" bedeutet, dass in der Datenbank jeder "Foreign‐Key" auf einen existierenden Datensatz zeigt ("referenziert"). Gegenbeispiel: Würde man im zweiten Datensatz der Tabelle Sitzungen, nach dem Projekt fragen, so bekäme man eine undefinierte Antwort. Die gesamte Datenbank hätte also keine referentielle Integrität. Erste Normalform Eine Datenbank ist in der ersten Normalform (1NF), wenn alle Attribute nur atomare Werte beinhalten. D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 21 AK-Automatisierungs und Kommunikationstechnik – TI – Technische Informatik NWT – Netzwerktechnik – www.munz-udo.de Gegenbeispiel: Solch ein "Fehler" passiert nur, wenn eine 1:N Relation nicht über eine eigene Tabelle aufgelöst wird. Es tauchen beispielsweise folgende Probleme auf: • • • Die Tabelle kann nach Projekten sortiert werden, nicht aber nach Sitzungen. Die einzelnen Datensätze haben unterschiedliche Länge Wie fügt man eine Sitzung hinzu, wie löscht man sie? Zweite Normalform Eine Datenbank befindet sich in der zweiten Normalform (2NF), wenn sie in der ersten Normalform ist und wenn ihre Tabellen keine redundanten Daten enthalten. (Daten tauchen nicht doppelt auf) Gegenbeispiel: Sitzungen Datum Projektname Teilnehmer Teilnehmer Teilnehmer 1 2 3 Erreichte Ziele Angestrebte Ziele 24.4.2001 Webmaster Oliver K. ‐ ‐ Forum installiert Präsentation für die 5.Klassen 31.4.2001 Webmaster Oliver K. ‐ ‐ Material nicht erhalten. Gemeinsamer Termin im Direktorat In diesem Fall tauchen alle Projekteigenschaften in den Sitzungen immer wieder auf. Aus dieser Datenredundanz ergeben sich einige Probleme. Angenommen der Projektname ändert sich in "Webdesign" oder der Name des ersten Teilnehmers war falsch geschrieben. Dann müssen alle Einträge in "Sitzungen" durchsucht und geändert werden. Lösung: Hier fehlt ein "Foreign‐Key" auf eine eigene Tabelle "Projekte". D:\Dokumente und Einstellungen\Munz\Desktop\Technische Informatik\Datenbanken\Einführung1.doc 22