4.14 Spannung, Strom und Leistung im Wechselstromkreis

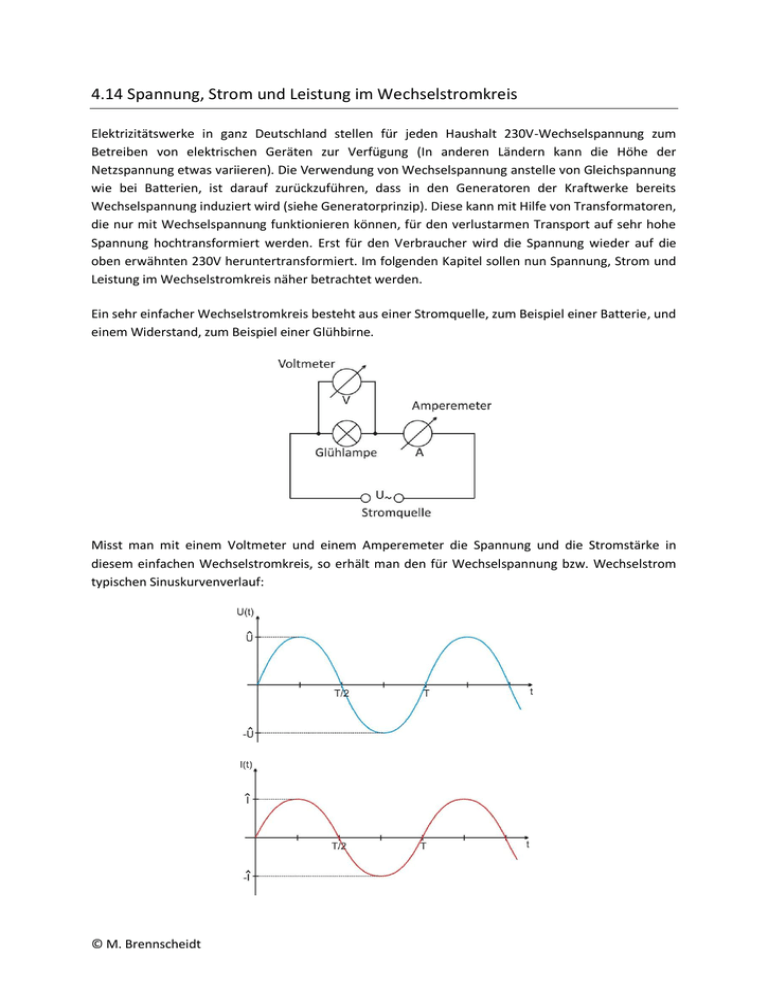
4.14 Spannung, Strom und Leistung im Wechselstromkreis
Elektrizitätswerke in ganz Deutschland stellen für jeden Haushalt 230V-Wechselspannung zum
Betreiben von elektrischen Geräten zur Verfügung (In anderen Ländern kann die Höhe der
Netzspannung etwas variieren). Die Verwendung von Wechselspannung anstelle von Gleichspannung
wie bei Batterien, ist darauf zurückzuführen, dass in den Generatoren der Kraftwerke bereits
Wechselspannung induziert wird (siehe Generatorprinzip). Diese kann mit Hilfe von Transformatoren,
die nur mit Wechselspannung funktionieren können, für den verlustarmen Transport auf sehr hohe
Spannung hochtransformiert werden. Erst für den Verbraucher wird die Spannung wieder auf die
oben erwähnten 230V heruntertransformiert. Im folgenden Kapitel sollen nun Spannung, Strom und
Leistung im Wechselstromkreis näher betrachtet werden.
Ein sehr einfacher Wechselstromkreis besteht aus einer Stromquelle, zum Beispiel einer Batterie, und
einem Widerstand, zum Beispiel einer Glühbirne.
Misst man mit einem Voltmeter und einem Amperemeter die Spannung und die Stromstärke in
diesem einfachen Wechselstromkreis, so erhält man den für Wechselspannung bzw. Wechselstrom
typischen Sinuskurvenverlauf:
© M. Brennscheidt
Mathematisch können Strom und Spannung ebenfalls durch Sinusfunktionen beschrieben werden.
Anmerkung:
An dieser Stelle soll explizit darauf hingewiesen werden, dass bei einem „normalen“ elektrischen
Widerstand wie zum Beispiel einer Glühbirne Spannung und Stromstärke in Phase sind. Das heißt,
dass die Stromstärke simultan mit der Spannung ansteigt bzw. abfällt. Dies ist zum Beispiel bei einem
Kondensator im Wechselstromkreis nicht so. Dort fließt zunächst ein Strom und erst dann baut sich
eine Spannung zwischen den Kondensatorplatten auf. Bei einer Spule ist es genau umgekehrt. Hier
baut sich zunächst eine Spannung auf und erst dann fließt aufgrund der Eigeninduktivität mit etwas
Verzögerung ein Strom durch die Spule.
Elektrische Leistung:
Die elektrische Leistung kann in einem Gleichstromkreis sehr einfach mit der Formel
berechnet werden. Diese Formel gilt auch für Wechselstromleistung. Da jedoch die Stromstärke und
die Spannung zu jedem Zeitpunkt verschieden sind, spricht man im Wechselstromkreis von
momentaner Wechselstromleistung. Diese ist somit abhängig von der Zeit :
Durch Einsetzen der Wechselspannung und des Wechselstroms ergibt sich dann:
Die momentane Wechselstromleistung setzt sich somit zusammen aus dem Produkt aus Scheitelspannung, Scheitelstromstärke und dem Quadrat der Sinusfunktion. Ziel der nun folgenden Überlegung soll es nun sein, den zeitlichen Verlauf der Wechselstromleistung darzustellen. Hierbei stellt
sich das Problem, dass das Quadrat einer Sinusfunktion aus dem Mathematikunterricht noch nicht
bekannt ist. Dieses wird deshalb mit Hilfe von Additionstheoremen aus der Trigonometrie durch eine
andere bereits bekannte Funktion ersetzt:
1.
2.
Löst man das zweite Additionstheorem nach
© M. Brennscheidt
(Trigonometrischer Pythagoras)
auf, so erhält man:
Durch Einsetzen in das erste Additionstheorem ergibt sich schließlich:
Hiermit kann man nun das Quadrat der Sinusfunktion durch die „bekannte“ Kosinusfunktion
ersetzen.
Die momentane Wechselstromleistung ändert sich somit periodisch mit der Winkelgeschwindigkeit
. Diese ist doppelt so groß hoch wie die Winkelgeschwindigkeit von Spannung und Stromstärke.
Somit ist auch die Frequenz der Momentanleistung doppelt so groß wie die Frequenz von Spannung
und Stromstärke:
In der Praxis ist meistens nicht der Momentanwert der Leistung von Interesse, sondern lediglich die
durchschnittliche Leistung einer Wechselstromquelle. Diese erhält man durch Bildung des
Mittelwertes von
. Da
gemittelt über eine Periode gleich Null ist, fällt der zweite
Summand der Momentanleistung bei der Bildung des Mittelwertes weg und es ergibt sich die
mittlere Leistung:
Da es für Rechnungen in der Praxis zweckmäßiger ist die gleiche Formel für Gleich- und Wechselstromleistung zu haben, wird die Formel für die mittlere Leistung noch etwas umgeformt:
© M. Brennscheidt
Mit der Effektivspannung
und der Effektivstromstärke
ergibt sich für die sog. Wirkleistung (mittlere Leistung):
Messgeräte zur Strom und Spannungsmessung zeigen in der Regel Effektivwerte von Strom und
Spannung an, so dass bei Gleich- und Wechselstromkreisen mit der gleichen Formel gerechnet
werden kann.
© M. Brennscheidt