Anwendungen von Reihen- und Parallelschaltung

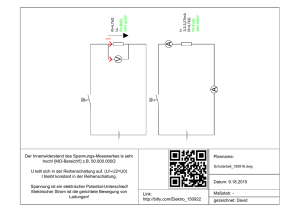
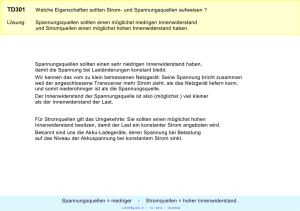
Anwendungen von Reihen- und Parallelschaltung
1.
Vorwiderstand
Ein Vorwiderstand RV wird verwendet, wenn an einem
elektrischen Bauteil eine bestimmte Spannung UB anliegen soll
und die von der Elektrizitätsquelle gelieferte Spannung Ug zu
groß ist.
Beispiel:
Ug = 20V
Glühlämpchen (6,0V/0,20A)
(siehe Skizze)
UV = 20V – 6V = 14V
RV =
2.
14 V
= 70 Ω
0,2 A
UV = ?
UB = 6,0V
V
V
RV
Ig = I = 0,2A
Ug = 20V
Schaltung elektrischer Geräte im Haushalt
Im Haushaltsnetz sind alle Geräte parallel geschaltet, denn:
• bei Reihenschaltung könnte man nur alle ein- oder alle aus- schalten
• jedes Gerät benötigt eine bestimmte Spannung. Bei der Reihenschaltung wäre die
jeweils anliegende Spannung davon abhängig, welche weiteren Geräte eingeschaltet
wären. Darum baut man alle Geräte so, dass sie 230V benötigen.
3.
Innenwiderstand und Schaltung von Strom- und Spannungsmessgeräten
3.1
Strommessgeräte
Ein Strommessgerät (Amperemeter) muss so in den Stromkreis geschaltet werden, dass der
ganze zu messende Strom durch es hindurchfließt.
Auch ein Strommessgerät besitzt einen Innenwiderstand Ri. Dieser muss sehr klein sein,
damit der Strom, der gemessen werden soll, nicht durch den Widerstand des Messgerätes
kleiner wird.
MERKE:
Reihenschaltung und sehr kleiner Innenwiderstand Ri
3.2
Spannungsmessgeräte
Spannungsmessgeräte (Voltmeter) sollen die Spannung messen, die z.B. über einem
Widerstand abfällt.
Sie müssen deshalb parallel angeschlossen werden (Spannung gleich), aber durch sie darf
(fast) kein Strom fließen (sonst würde der Strom durch den Widerstand kleiner werden). Der
Innenwiderstand eines Spannungsmessgerätes muss also sehr groß sein.
MERKE:
Parallelschaltung und sehr großer Widerstand
4.
Innenwiderstand von Elektrizitätsquellen
Elektrizitätsquellen besitzen selbst einen Widerstand, den Innenwiderstand Ri.
Elektrizitätsquelle
Man kann sich eine Elektrizitätsquelle so
vorstellen (siehe Skizze):
Die Ruhe-, Leerlauf- oder Quellenspannung U0
Ri
wird
dann
gemessen,
wenn
nur
ein
U0
Spannungsmessgerät an die Elektrizitätsquelle
angeschlossen ist. (Ra = ∞)
Wird ein weiterer Widerstand (Außenwiderstand Ra) angeschlossen, so heißt die am äußeren
Widerstand gemessene Spannung Belastungsspannung oder Betriebsspannung UB.
Die Belastungsspannung ist kleiner als die Leerlaufspannung, denn am Innenwiderstand der
Spannungsquelle fällt die Spannung Ui = R i ⋅ I ab (Reihenschaltung).
Also: UB = U0 – Ui = U0 – R i ⋅ I
Bei Belastung sinkt die Leerlaufspannung U0 um die Teilspannung Ui = R i ⋅ I am
Innenwiderstand Ri der Spannungsquelle.
Die Belastungsspannung UB sinkt, wenn der äußere Widerstand Ra kleiner wird.
Erklärung:
Die Widerstände Ri und Ra sind in Reihe geschaltet, also teilt sich die
Spannung auf die einzelnen Widerstände auf.
(Am kleineren Widerstand fällt die kleinere Spannung ab.)
Die Kurzschlussstromstärke IK wird gemessen, wenn der äußere Widerstand Ra = 0 Ω ist.
Die Belastungsspannung ist dann 0 V, denn über einem Widerstand von 0 Ω fällt keine
Spannung ab.
Der Innenwiderstand Ri der Elektrizitätsquelle berechnet sich dann so:
U0
UB = 0 V = U0 – R i ⋅ IK ⇒ R i =
(siehe AP 99 B).
IK
5.
Stromrichtige und spannungsrichtige Messung
5.1
Stromrichtig
V
Im Strommessgerät fließt derselbe Strom wie im Widerstand
(Reihenschaltung).
Die gemessene Spannung ist „falsch“, da über R und RA
(Innenwiderstand des Strommessgerätes) eine Spannung
Ug = UR + URA abfällt.
5.2
R
A
Spannungsrichtig
Am Spannungsmessgerät liegt die Spannung an, die am
Widerstand anliegt (Parallelschaltung).
Der gemessene Strom ist „falsch“, da die Gesamtstromstärke
Ig = IR + IA beträgt.
V
R
A
Nicht mehr im Lehrplan!
6.
Spannungsteilerschaltung
Ersatzschaltbild:
V
V
R1
R1
R2
R2
6.1
Unbelasteter Spannungsteiler
Durch das Voltmeter fließt (fast) kein Strom. Wir messen dort die Spannung U2, die nur über
dem Rest des Schiebewiderstands (entspricht dem Teilwiderstand R2) abfällt.
6.2
Belasteter Spannungsteiler
Wird statt dem Voltmeter ein elektrisches Bauteil B verwendet, durch das ein nicht zu
vernachlässigender Strom fließt, so ändert sich der Gesamtwiderstand. Wir haben
1
R1 +
1
1 .
jetzt eine Kombination aus Reihen- und Parallelschaltung: Rges =
+
R 2 RB
UB = Rges . I
Damit ändert sich auch die am Bauteil anliegende Spannung UB:
7.
Messbereichserweiterung bei Strom- und Spannungsmessgeräten
7.1
Wir haben ein Spannungsmessgerät, das nur bis 1,0 V Spannungen messen kann.
Mit diesem Messgerät möchten wir gerne noch größere Spannungen messen.
Wie geht das ?
RV = ?
Wir erweitern den Messbereich durch einen „Trick:“:
Wir schalten einen Vorwiderstand vor das Messgerät
(Reihenschaltung) und berechnen die eigentliche
UV
Spannung mithilfe der Formel
U1 R 1
=
für die Reihenschaltung (siehe FS. S
)
U2 R 2
(am größeren Widerstand fällt die größere Spannung ab)
RV
Am Vorwiderstand fällt ein Teil der Spannung ab, die insgesamt
zu groß für das Messgerät wäre.
Wir berechnen die Größe von RV ,(das Messgerät hat den
Innenwiderstand RM).
Wenn wir den Messbereich um das 10 - fache erweitern wollen:
1
Die gemessene Spannung UM muss
von der anliegenden Spannung Ug sein.
10
9
Dann müssen am Vorwiderstand
von Ug abfallen.
10
9
RM ⋅
Ug
U1 R 1
10
=
= RM ⋅ 9
Mit der Formel
: RV =
1
U2 R 2
Ug
10
Allgemein gilt, wenn der Messbereich auf das n-fache erweitert werden soll:
RV = RM . (n-1)
UM
7.2
Wir haben ein Strommessgerät, das nur bis 1,0 A Stromstärken messen kann.
Wir möchten gerne Stromstärken messen, die größer sind.
Wir leiten den zu großen Strom außen vorbei (parallel) und messen den Rest.
Aus dem Reststrom können wir den ganzen, ursprünglichen Strom bestimmen, denn
I1 R 2
=
es gilt:
(UMGEKEHRT!)
(FS Seite
)
I2 R 1
(durch den kleineren Widerstand fließt der größere Strom)
Wir berechnen die Größe des Nebenwiderstands Rn (das Messgerät hat
Innenwiderstand RM), wenn wir den Messbereich um das 10 - fache erweitern wollen:
1
Der gemessene Strom IM muss
von dem anliegenden Strom Ig sein.
10
9
Dann müssen durch den Nebenwiderstand
von Ig fließen.
10
Mit der Formel :
I1 R 2
=
I2 R 1
IM R n
=
In R M
den
1
⋅I ⋅R
IM ⋅ R M 10 g M 1
=
= ⋅ RM
Rn =
9
In
9
⋅ Ig
10
Allgemein gilt, wenn der Messbereich auf das n-fache erweitert werden soll:
Rn =
1
⋅ RM
n− 1
Aber: Wenn der neue Messbereich kein ganzes Vielfaches des alten ist, geht es ohne die
Formeln für RV bzw. Rn einfacher!