WHB11 - Mathematik Klausurübungen für die
Werbung

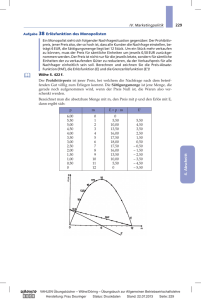
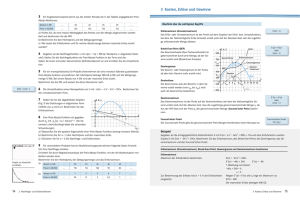
WHB11 - Mathematik Klausurübungen für die Klausur am 3. Juni 2015 Datum: Mai 2015 Themen: • Marktgleichgewicht, Prohibitivpreis, Sättigungsmenge, Angebots- und Nachfrageüberschuss • Monopolist: Preis-Absatz-Funktion, Erlösfunktion, Sättigungsmenge, erlösmaximale Menge, maximaler Erlös • Monopolist: Gewinnfunktion, Gewinnzone, gewinnmaximale Menge, maximaler Gewinn Übungen zum Thema Marktgleichgewicht: Aufgabe 1 Auf dem Markt für ein bestimmtes Gut können Angebot und Nachfrage gemäß folgender Funktionen beschrieben werden. Angebotsfunktion pA(x) = x + 5 Nachfragefunktion pN(x) = -0,2x + 20 a) Berechnen Sie die Mengen, die bei einem Preis von 10 GE/ME angeboten und nachgefragt werden und geben Sie an, welches Marktungleichgewicht (Angebotsüberschuss oder Nachfrageüberschuss) vorliegt. b) Bestimmen Sie das Marktgleichgewicht. c) Geben Sie den ökonomischen Definitionsbereich der Nachfragefunktion an. d) Stellen Sie die Marktsituation in einer Skizze dar und kennzeichnen Sie die Sättigungsmenge und den Höchstpreis (Prohibitivpreis). Aufgabe 2 Auf dem Markt für ein bestimmtes Gut können Angebot und Nachfrage gemäß folgender Funktionen beschrieben werden. Angebotsfunktion pA(x) = 1 x + 28 3 Nachfragefunktion pN(x) = -0,6x + 70 a) Berechnen Sie die Mengen, die bei einem Preis von 60 GE/ME angeboten und nachgefragt werden und geben Sie an, welches Marktungleichgewicht (Angebotsüberschuss oder Nachfrageüberschuss) vorliegt. b) Bestimmen Sie das Marktgleichgewicht. c) Geben Sie den ökonomischen Definitionsbereich der Nachfragefunktion an. d) Stellen Sie die Marktsituation in einer Skizze dar und kennzeichnen Sie die Sättigungsmenge und den Höchstpreis (Prohibitivpreis). Aufgabe 3 Auf dem Markt für ein bestimmtes Gut können Angebot und Nachfrage gemäß folgender Funktionen beschrieben werden. Angebotsfunktion pA(x) = 2x + 2 Nachfragefunktion pN(x) = 32 – 0,5x² a) Berechnen Sie die Mengen, die bei einem Preis von 16 GE/ME angeboten und nachgefragt werden und geben Sie an, welches Marktungleichgewicht (Angebotsüberschuss oder Nachfrageüberschuss) vorliegt. b) Bestimmen Sie das Marktgleichgewicht. c) Geben Sie den ökonomischen Definitionsbereich der Nachfragefunktion an. d) Stellen Sie die Marktsituation in einer Skizze dar und kennzeichnen Sie die Sättigungsmenge und den Höchstpreis (Prohibitivpreis). Hinweise: a) Zwei Mengen (x-Werte) ausrechnen und vergleichen. b) Schnittpunkt berechnen c) y-Abschnitte, Nullstelle und Schnittpunkt aus b) verwenden. Sättigungsmenge ausrechnen. c) Dök = [0;Sättigungsmenge] WHB11 - Mathematik Klausurübungen für die Klausur am 3. Juni 2015 Datum: Mai 2015 Übungen zum Thema Monopolist Aufgabe 4 Für die Nachfrage nach einem Produkt gilt die Nachfragefunktion p(x) = -12x + 600. a) Bestimmen Sie den Höchstpreis und die Sättigungsmenge. b) Bestimmen Sie die Erlösfunktion. c) Bestimmen Sie den ökonomischen Definitionsbereich. d) Bestimmen Sie die erlösmaximale Menge sowie den maximalen Erlös! e) Skizzieren Sie die beiden Funktionen in einen Koordinatensystem. f) Erklären Sie die Begriffe Sättigungsmenge und Höchstpreis. Aufgabe 5 Ein Monopolist bestimmt seine Preise auf Basis der Preis-Absatz-Funktion p(x) = - 30x + 480. a) Bestimmen Sie den Höchstpreis und die Sättigungsmenge. b) Bestimmen Sie die Erlösfunktion. c) Bestimmen Sie den ökonomischen Definitionsbereich. d) Bestimmen Sie die erlösmaximale Menge sowie den maximalen Erlös! e) Skizzieren Sie die beiden Funktionen in einen Koordinatensystem. f) Erklären Sie die Begriffe Sättigungsmenge und Höchstpreis. Aufgabe 6 Ein Monopolist arbeitet mit einer linearen Preis-Absatzfunktion p(x) = -10x + 70. Seine Kostenfunktion ist linear. Die fixen Kosten betragen 50 GE und die variablen Stückkosten 15 GE. a) Bestimmen Sie den Höchstpreis und die Sättigungsmenge. b) Bestimmen Sie die Kostenfunktion, die Erlösfunktion und die Gewinnfunktion! c) Bestimmen Sie den ökonomischen Definitionsbereich. d) Bestimmen Sie die erlösmaximale Menge sowie den maximalen Erlös! e) Bestimmen Sie die Gewinnzone! f) Bestimmen Sie die gewinnmaximale Menge und den maximalen Gewinn! g) Skizzieren Sie die vier Funktionen in einen Koordinatensystem. Aufgabe 7 Ein Monopolist bestimmt seine Preise auf Basis der Preis-Absatz-Funktion p(x) = - 5x + 850. Bei der Produktion fallen variable Stückkosten in Höhe von 20 € und fixe Kosten in Höhe von 500 € an. a) Bestimmen Sie den Höchstpreis und die Sättigungsmenge. b) Bestimmen Sie die Kostenfunktion, die Erlösfunktion und die Gewinnfunktion! c) Bestimmen Sie den ökonomischen Definitionsbereich. d) Bestimmen Sie die erlösmaximale Menge sowie den maximalen Erlös! e) Bestimmen Sie die Gewinnzone! f) Bestimmen Sie die gewinnmaximale Menge und den maximalen Gewinn! g) Skizzieren Sie die vier Funktionen in einen Koordinatensystem. Aufgabe 8 Ein Monopolist kalkuliert seine Produktionsplanung aufgrund der Gewinnfunktion G(x) = -0,3x² + 3,3x – 3. a) Berechnen Sie die Gewinnschwelle und die Gewinngrenze und geben Sie die Gewinnzone an. b) Der Monopolist weiß bereits, dass die gewinnmaximale Produktionsmenge bei 5,5 ME liegt und der maximale Gewinn 6,10 GE beträgt. Zeichnen Sie den Graphen der Gewinnfunktion unter Berücksichtigung der Ergebnisse aus a) in ein Koordinatensystem. (Hinweis: x-Achse: 0 ≤ x ≤ 12; y-Achse: -5 ≤ y ≤ 10) WHB11 - Mathematik Klausurübungen für die Klausur am 3. Juni 2015 Datum: Mai 2015 Aufgabe 9 Der Produzent einer Spezialkamera ist Monopolist. Die gesamten Produktionskosten ergeben sich aus der Funktion K(x) = 0,2x + 1,6. Die Preispolitik erfolgt auf Grundlage einer linearen Preis-Absatz-Funktion. Bei einem Angebot von x Stück kann ein Stückpreis von p(x) erzielt werden, wobei gilt: p(x) = -0,2x + 2. a) Bestimmen Sie den Höchstpreis und die Sättigungsmenge. b) Bestimmen Sie die Erlösfunktion und die Gewinnfunktion! c) Bestimmen Sie den ökonomischen Definitionsbereich. d) Bestimmen Sie die erlösmaximale Menge sowie den maximalen Erlös! e) Bestimmen Sie die Gewinnzone! f) Bestimmen Sie die gewinnmaximale Menge und den maximalen Gewinn! g) Skizzieren Sie die vier Funktionen in einen Koordinatensystem. Aufgabe 10 Der Produzent einer Werkzeugmaschine ist Monopolist. Die gesamten Produktionskosten ergeben sich aus der Funktion K(x) = 4.000x + 32.000. Die Preispolitik erfolgt auf Grundlage einer linearen Preis-Absatz-Funktion. Bei einem Angebot von x Stück kann ein Stückpreis von p(x) erzielt werden, wobei gilt: p(x) = -4.000x + 40.000. a) Bestimmen Sie den Höchstpreis und die Sättigungsmenge. b) Bestimmen Sie die Erlösfunktion und die Gewinnfunktion! c) Bestimmen Sie den ökonomischen Definitionsbereich. d) Bestimmen Sie die erlösmaximale Menge sowie den maximalen Erlös! e) Bestimmen Sie die Gewinnzone! f) Bestimmen Sie die gewinnmaximale Menge und den maximalen Gewinn! g) Skizzieren Sie die vier Funktionen in einen Koordinatensystem. Zusatzaufgabe: Überlegen Sie für die Monopolisten in Aufgabe 9 und 10 welchen Preis Sie für die Spezialkameras bzw. die Werkzeugmaschinen verlangen sollten. (Stichwort: Cournotscher Punkt) Lösungen: Aufgabe 1: a) angebotene Menge: 5 ME, nachgefragte Menge: 50 ME => Nachfrageüberschuss: 45 ME b) (12,5/17,5) c) Dök = [0;100] Aufgabe 2: a) angebotene Menge: 96 ME, nachgefragte Menge: 16,67 ME => Angebotsüberschuss: 79,33 ME b) (45/43) c) Dök = [0;116,67] Aufgabe 3: d) angebotene Menge: 7 ME, nachgefragte Menge: 5,67 ME => Angebotsüberschuss: 1,33 ME e) (6/14) f) Dök = [0;8] Aufgabe 4: a) Höchstpreis: 600 GE/ME; Sättigungsmenge: 50 ME b) E(x) = -12x² + 600x c) Dök = [0;50] d) Erlösmaximale Menge: 25 ME und maximaler Erlös: 7.500 GE Aufgabe 5: a) Höchstpreis: 480 GE/ME; Sättigungsmenge: 16 ME b) E(x) = -30x² + 480x c) Dök = [0;16] d) Erlösmaximale Menge: 8 ME und maximaler Erlös: 1.920 GE Aufgabe 6: a) Höchstpreis: 70 GE/ME; Sättigungsmenge: 7 ME b) K(x) = 15x + 50; E(x) = -12x² + 600x; G(x) = -12x² + 585x - 50 WHB11 - Mathematik Klausurübungen für die Klausur am 3. Juni 2015 c) d) e) f) Datum: Mai 2015 Dök = [0;7] Erlösmaximale Menge: 3,5 ME und maximaler Erlös: 122,5 GE Gewinnzone: [1,15; 4,35] Gewinnmaximale Menge: 2,75 ME und maximaler Gewinn: 25,625 GE Aufgabe 7: a) Höchstpreis: 850 GE/ME; Sättigungsmenge: 170 ME b) K(x) = 20x+500; E(x) = -5x² + 850x; G(x) = -5x² + 830x - 500 c) Dök = [0;170] d) Erlösmaximale Menge: 85 ME und maximaler Erlös: 36.125 GE e) Gewinnzone: [0,60; 165,40] f) Gewinnmaximale Menge: 83 ME und maximaler Gewinn: 33.945 GE Aufgabe 8: a) Gewinnzone: [1;10] b) G(x) 10 8 6 4 2 O 2 4 6 8 10 12 x -2 -4 -6 Aufgabe 9: a) Höchstpreis: 2 GE/ME; Sättigungsmenge: 10 ME b) E(x) = -0,2x² + 1,6x; G(x) = -0,2x² + 1,8x – 1,6 c) Dök = [0;10] d) Erlösmaximale Menge: 5 ME und maximaler Erlös: 5 GE e) Gewinnzone: [1; 8] f) Gewinnmaximale Menge: 4,5 ME und maximaler Gewinn: 2,45 GE Aufgabe 10: a) Höchstpreis: 40.000 GE/ME; Sättigungsmenge: 10 ME b) E(x) = -4.000x² + 40.000x; G(x) = -0,2x² + 1,8x – 1,6 c) Dök = [0;10] d) Erlösmaximale Menge: 5 ME und maximaler Erlös: 100.000 GE e) Gewinnzone: [1; 8] f) Gewinnmaximale Menge: 4,5 ME und maximaler Gewinn: 49.000 GE Zusatzaufgabe: Einsetzen der gewinnmaximalen Menge in Preis-Absatz-Funktion ergibt: Aufgabe 9: p(4,5) = 1,1 GE/ME. Die Spezialkamera sollte 1,1 GE/ME kosten. Cournotscher Punkt (4,5/1,1) Aufgabe 10: p(4,5) = 22.000. Die Werkzeugmaschine sollte 22.000 GE/ME kosten. Cournotscher Punkt (4,5/22.000)