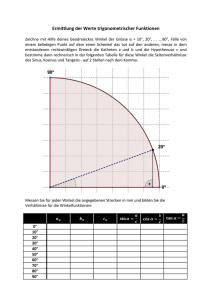
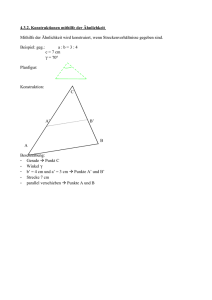
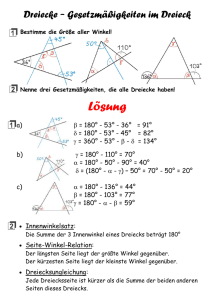
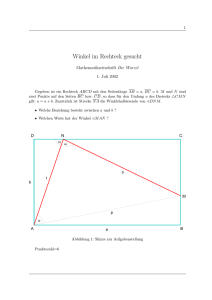
Mathematische Billardspiele

Mathematische Billardspiele
am Tag der Mathematik
an der Carl von Ossietzky Universität Oldenburg
am 5. November 2003
Zusammenfassung:
Der Lauf einer Billardkugel hängt entscheidend von der Geometrie des Billardtisches
ab. Unterschiedliche Formen der Banden führen auf ganz verschiedene dynamische
Phänomene.
Am Beispiel eines Billardtisches mit der geometrischen Gestalt einer Ellipse sind entweder alle Bahnen der Kugeln periodisch oder keine. Im letzteren Fall kommt die Bahn
einer Billardkugel jedem Punkt auf dem Rand des Tisches beliebig oft beliebig nah.
Doch existieren in beiden Fällen sogenannte ,,Konstanten der Bewegung”: Es gibt eine
Ellipse oder eine Hyperbel mit denselben Brennpunkten wie bei der Billardtisch-Ellipse,
die jeder geradlinige Teil der Bahn tangential berührt.
Billard auf einem kreisrunden Tisch
Hier geht es um die Bewegung eines Billardballes auf Tischen mit unterschiedlich geformten Banden. Wenden wir uns zunächst einem kreisrunden Billardtisch zu. Neben der Forderung, dass sich eine Kugel abseits vom Rand nur
geradlinig fortbewegt, braucht man als Voraussetzung noch das Reflexionsgesetz: Stößt die Billardkugel in einem gewissen Winkel auf die Bande, so wird
sie mit demselben Winkel reflektiert.
Abbildung 1: Beispiel, bei dem die Kugel im 45o -Winkel auftrifft
Bei der Definition von Einfalls- und Ausfallswinkel muss man sich behelfen,
weil ja hier keine geraden Begrenzungsstücke vorliegen, sondern gekrümmte.
Deshalb definiert man Einfalls- und Ausfallswinkel in einem Punkt der Ellipse
durch den Einfalls- und Ausfallswinkel, den man an der Tangente an die Ellipse
in diesem Punkt haben würde. Eine Tangente 1 ist die Gerade, die die Ellipse
in diesem Punkt berührt. Sie ist diejenige Gerade, die dem Verlauf der Kurve
in der Nähe des Punktes am nächsten kommt.
1
tangere (lat.): berühren
1
Nach diesem Reflexionsprinzip würde auch ein Lichtstrahl an einem kreisrunden Spiegel reflektiert. Ob wir nun einen solchen Versuch in der Optik oder in
diesem Problem der Mechanik mit Billardkugeln betrachten: Wir nehmen dafür
das gleiche mathematische Modell. Die eingezeichneten Strecken stehen für den
Weg, auf denen die Billiardkugel rollt bzw. entlang dessen die Lichtstrahlen verlaufen. Und die Bande des Billardtisches kann ebenso gut einen kreisförmigen
Spiegel beschreiben.
In unserer Idealisierung kümmern wir uns nicht um Fragen der Reibung; ja im
Grunde ist uns selbst die Geschwindigkeit gleichgültig, mit welcher die Kugel
ihren Weg zurücklegt. Dies mag angesichts des Themas der Dynamik zunächst
verwundern. Wir gehen davon aus, dass die Kugel mit konstanter Geschwindigkeit immer weiter rollt, und interessieren uns für den Weg, den sie zurücklegt.
Unser dynamisches System wird durch die Folge der Punkte beschrieben, an
denen die Kugel auf die Bande trifft. Zwischen zwei Punkten auf der Bande ist
die Bewegung gleichförmig und geradlinig; an einem Bandenpunkt wechselt die
Richtung.
Periodische Bahnen
Als erstes Beispiel betrachten wir eine Billardkugel, die in einem Winkel von
45o auf die Bande trifft. Auf einer Kreislinie von einem gewissen Radius – der
Einfachheit halber nehmen wir den Radius 1 – möchten wir diese Dynamik
beschreiben, wenn die Kugel zum ersten Mal mit einem 45o -Winkel vom Süden
kommend im östlichsten Punkt mit den Koordinaten (1, 0) auftrifft. Dort wird
sie mit demselben Winkel reflektiert und bewegt sich geradlinig auf den Nordpol
zu, wird wieder mit 45o reflektiert und läuft zum Westpol, dann zum Südpol und
dann schließt sich der Kreis im wahrsten Sinne des Wortes. Die Kugel durchläuft
immer wieder dieselben Strecken; man nennt so eine Bahn der Kugel periodisch.
A: Erstes
Auftreffen
B:
Zweites
Auftreffen
C: Drittes
Auftreffen
D: Viertes
Auftreffen
E:
Fünftes
Auftreffen
Abbildung 2: Dynamik beim Auftreffen von 45o
Wenn wir nur die Bahn der Bandenpunkte betrachten, kommt man von einem
Auftreffpunkt zum nächsten durch eine Rotation R90o um 90o . Führt man diese
viermal hintereinander aus, so kommt man an den Ausgangspunkt zurück. Diese
Vierteldrehung, die Rotation um 14 ·360o , also 90o , ist ein Beispiel für Rotationen,
die periodische Bahnen liefern. Gleichgültig, mit welchem Punkt man startet,
er liegt wieder auf dem Ausgangspunkt, wenn man viermal mit 90o rotiert.
2
Allgemeiner hat jede Rotation zu einem Winkel mit einem rationalen Vielfachen
von 360o , also solche, die man durch Multiplikation von 360o mit einer Bruchzahl
erhält, periodische Bahnen. Denn ist nz die Bruchzahl mit Zähler z und Nenner
n, so bringt eine Rotation zum Winkel α = nz · 360o , wenn man sie n-mal
hintereinander ausführt, jeden Punkt wieder zu seinem Ausgangspunkt zurück.
P1
P4
P5
P7
P2
P6
P3
Abbildung 3: Eine periodische Bahn mit n = 7 und z = 2
Das Rotationsmodell für die Bandenpunkte einer Bahn ist in der Tat nur ein
anderes Modell für dieselbe Sache bei der Billardkugelbahn. Schon bei dem
Beispiel eingangs, bei dem die Kugel mit einem Winkel von 45o auf die Bande
trifft, wurde diese Tatsache verschwiegen, weil sie dort so offensichtlich ist: Wenn
eine Billardkugel mit einem Winkel von 45o auf den Ostpol trifft, wird sie genau
so reflektiert, dass sie auch auf alle weiteren Bandenpunkte mit diesem Winkel
auftrifft.
Das Reflexionsgesetz beim kreisförmigen Billard
Dies ist nun kein Spezialfall bei diesem Winkel, wie ein wenig Kreisgeometrie
zeigt: Wir wollen zeigen, dass nach einem Berührpunkt P1 , auf den die Kugel
mit irgendeinem Winkel α trifft, der nächste Berührpunkt P2 unter dem gleichen
Winkel α angesteuert wird.
Dazu ziehen wir vom Mittelpunkt zwei Strecken zu den Punkten P1 bzw. P2 . Auf
diesen Strecken stehen die Tangenten an den Kreis in P1 und in P2 senkrecht.
Der Winkel zwischen den Strecken M P1 und P1 P2 besitzt deshalb die Größe
90o − α. Da das Dreieck mit den Eckpunkten M , P1 und P2 gleichschenklig ist,
handelt es sich bei dem Auftreffwinkel in P2 um einen derselben Größe. Wegen
3
M
o
90 − α
P1
90o − α
α
α
P2
der Orthogonalität der Strecke M P2 zur Tangente in P2 sieht man, dass der
Reflexionswinkel im Punkt P2 die Größe 900 − (90o − α) = α besitzt.
Nicht-periodische Bahnen
Ein völlig anderes Bild erhält man, wenn als Winkel nicht nur rationale Vielfache von 360o erlaubt sind, sondern auch irrationale. Machen wir uns zunächst
klar, dass es dann keine periodischen Bahnen gibt. In der Beschreibung mit
Rotationen bedeutet eine periodische Bahn, dass ein Punkt nach endlich vielen
Drehungen um denselben Winkel α wieder zum Ausgangspunkt zurückkehrt.
Mit anderen Worten: Es gibt eine natürliche Zahl n – nämlich die Anzahl der
Bandenberührungen, bis der Ball wieder zum Ausgangspunkt zurückkehrt, –
so dass das n-fache des Winkels α ein Vielfaches von 360o ist: Für eine andere
natürliche Zahl z mit 2 · z < n ist
n · α = z · 360o .
Also können wir die Beobachtung festhalten, dass eine Bahn genau in dem Fall
periodisch ist, dass α ein rationales Vielfaches von 360o ist. Denn wenn wir die
Gleichung durch n dividieren, erhalten wir
α=
mit der rationalen Zahl
z
n
z
· 360o
n
mit Zähler z und Nenner n.
Dichte Bahnen
Nun wollen wir untersuchen, was bei einem Winkel α geschieht, der irrationales Vielfaches von 360o ist, z. B. α = √117 · 360o . Wir wissen schon, dass für
solche Winkel eine Billardkugel nie mehr an ihren Ausgangspunkt zurückkommen kann, selbst wenn sie unendlich oft an der Bande reflektiert wird. Jeder
4
Punkt auf der Band wird also höchstens einmal getroffen, wenn der Rotationswinkel ein irrationales Vielfaches von 360o ist. Wir werden nun sehen, dass bei
einem solchen Winkel eine Billardkugel jedem Punkt auf der Bande beliebig oft
beliebig nahe kommt.
Wir haben also einen Startpunkt P1 und schießen die Billardkugel in einem
irrationalen Winkel auf den Punkt P2 und erhalten so nach und nach eine Folge
von Berührpunkten P1 , P2 , P3 , . . . , Pn , . . . auf der Kreislinie. Um zu zeigen, dass
die Kugel einem Punkt Q auf der Kreislinie beliebig oft beliebig nahe kommt,
müssen wir folgendes zeigen: Wenn wir um Q ein noch so kleines Kreissegment
wählen (gegeben beispielsweise durch einen Winkel um den Mittelpunkt, so dass
die Winkelhalbierende durch Q verläuft), wird irgendwann die Kugel innerhalb
dieses Kreissegments einen Punkt der Bande berühren.
Abbildung 4: Gleichlange Schubfächer-Einteilung des Kreisrandes
Wir können ein kleineres Kreissegmentwählen, das durch ein rationales Vielfaches n1 · 360o gegeben ist, so dass in das vorgegebene Kreissegment dieses
zweimal2 hineinpasst und der Punkt Q in der Mitte zwischen den beiden Segmente liegt. Denn wenn wir das Segment kleiner machen, erschweren wir uns die
Aufgabe ja eher noch. Die Kreislinie wird in n Segmente dieser Größe zerteilt.
Wenn wir nun mindestens n + 1 Bandenberührungen warten, können wir sicher
sein, dass in irgendeinem der n Segmente zwei Bandenberührungen stattfinden. Man kann nicht n + 1 Punkte auf n Segmente verteilen, so dass in keinem
Segment mehr als ein Punkt liegt. Dies ist das ein Prinzip, das der Mathematiker Dirichlet3 für seine Studierenden Schubfachprinzip“ genannt hat: Wenn
”
man n + k Dinge in n Schubfächer legen möchte, liegen in einem Schubfach
mindestens zwei Dinge.
Da der Kreis nun aber völlig symmetrisch ist, können wir die Situation so
herumdrehen, dass unser kleines Segment nach endlichen Schritten die Kugel
bekommt. Denn wir haben nun in einem der Kreissegmente der Größe n1 · 360o
einen Punkt Pk und einen weiteren Punkt Pk+l . Da Rotationen aber nun einmal
völlig symmetrische Operationen sind, weiss man über den ursprünglich gewählten Punkt P1 = Q, dass in dem doppelten Kreissegment der Größe n2 ·360o auch
der Punkt P1+l liegt. Da wir bei unserer Argumentation nicht genau wissen
konnten, wie die Punkte P1 und P1+l angeordnet sind, haben wir zu dem Trick
gegriffen, eine noch feinere Zerlegung des Kreissegments zu wählen, so dass
2
Dass es zweimal hineinpassen soll, ist lediglich ein kleiner Trick, der unten erläutert wird,
aber getrost überlesen werden kann.
3
∗ 1805 (Düren), † 1859 (Göttingen)
5
wir sicher sein können, dass beide Punkte im ursprünglich gewählten Segment
enhalten sind.
Wir haben also zwei verschiedene Klassen von Bahnen kennengelernt: Die periodischen durchlaufen immer wieder einen Zyklus von endlich vielen Bandenberührungen. Die nicht-periodischen berühren keinen Bandenpunkt zweimal
und kommen jedem Bandenpunkt beliebig oft beliebig nah. Eine Menge, die
jedem Punkt der umgebenden Menge beliebig oft beliebig nahe kommt, nennt
man dicht in der umgebenden Menge. Die Berührpunkte auf der Bande im
nicht-periodischen Fall liegt dicht in der Menge aller Bandenpunkte. Es bedarf
– dies sei am Rande bemerkt – einiger Vorbereitungen und Definitionen, um zu
verstehen, dass es sehr viele Punkte entlang der Bande gibt, die nicht getroffen
werden.4
Bahnen auf einem ellipsenförmigen Billardtisch
Abbildung 5: Ein ellipsenförmiger Billardtisch
Ein Kreis in der Ebene oder eine Kugel im Raum gelten seit jeher als perfekte geometrische Formen. Eine – unvollkommenere – Verallgemeinerung eines
Kreises stellt eine Ellipse dar. Der griechische Ursprung des Wortes Ellipse bezeichnet einen Mangel“, nämlich die Abweichung vom perfekten Kreis. Am
”
einfachsten zu beschreiben ist sie als sogenannte Gärtnerellipse.
l1
l2
F1
F2
Abbildung 6: Gärtnerellipse
So kann ein Gärtner sein weidendes Schaf unter Kontrolle halten: Zwei Pflöcke
werden in den Boden geschlagen und die Enden eines Seiles an dem einen und
4
Wer den Begriffe der Abzählbarkeit kennt sieht ein, dass die Menge der Berührpunkte
abzählbar und die Menge der Bandenpunkte überabzählbar ist.
6
an dem anderen befestigt und durch das Halsband des Schafes gefädelt. Eine
Ellipse ist nun der Rand der Fläche, auf der das Schaf grasen kann.
Die beiden Stellen, an denen die Pflöcke in dem Boden stecken, werden Brennpunkte genannt; denn ein ellipsenförmiger Spiegel hat die Eigenschaft, dass jeder
Lichtstrahl, der von dem einen Brennpunkt ausgesandt und an dem Spiegel reflektiert wird, geht auch durch den anderen Brennpunkt.
F1
F2
Abbildung 7: Lichtstrahlen, die von einem der Brennpunkte F1 bzw. F2 ausgehen
Abhörsichere Ferngespräche im Mittelalter
In der Kathedrale La Chaise du Dieu hat der salle des échos, in dem die Beichte
abgenommen wurde, die Form einer Ellipse. Allerdings findet man dort keine
Beichtstühle; zwei Plätze sind markiert: An den beiden Brennpunkten der Ellipse etliche Meter voneinander. An dem einen Brennpunkt nahm ein Geistlicher
die Beichte ab – die beichtende Person stand entfernt auf dem anderen Brennpunkt. Wenn man normal spricht, ist dies in einer Kathedrale schon wenige
Meter entfernt nicht mehr zu verstehen. Die Schallwellen werden an den Mauern reflektiert und verlieren sich in der Weite des Raumes.
Die Brennpunkteigenschaft bewirkt nun allerdings etwas Besonderes, wenn Schallwellen von einem Brennpunkt ausgehen: Diese Wellen durchqueren auf ihren
unterschiedlichen Wegen alle den anderen Brennpunkt, und zwar zur gleichen
Zeit. Das liegt an der Gärtnerkonstruktion: Alle Wege, die von einem Brennpunkt zum anderen zurückgelegt werden, stimmen in ihrer Länge überein.
Die Worte des Beichtenden und des Beichtvaters sind also für Personen in der
Kirche, die sich nicht in der Nähe der Brennpunkte aufhalten, kaum vernehmbar; in der Tat kommt das, was an einem Brennpunkt normal gesprochen wird,
an dem anderen gut verständlich an.
Für das elliptische Billardspiel bedeutet dies: Schießt man eine Kugel von einem
Brennpunkt aus an den Rand, dann wird sie dort so reflektiert, dass sie durch
den anderen Brennpunkt läuft. Gehen wir wieder davon aus, dass diese Bahn
niemals stoppt, so wird die Kugel zwischen zwei Randberührungen abwechselnd
7
durch einen der beiden Brennpunkte laufen. Etwas mathematischer ausgedrückt
sind die Punkte auf der Ellipse durch die Eigenschaft definiert, dass die Summe
der Abstände zu den beiden Brennpunkten F1 und F2 konstant ist – nämlich
entsprechend der Länge des Seiles.
Nach dem Billiardspiel und der optischen Anwendung auf ellipsenförmige Spiegel ist unser Modell auch auf akustische Wellen in einem ellipsenförmigen Raum
anwendbar. Die ellipsenförmige Geometrie des umgebenden Raumes, das Reflexionsgesetz und die geradlinigen Verbindungsstrecken führen in allen drei Fällen
auf dasselbe Modell.
Die Bahnen einer Kugel beim elliptischen Billard
Wir nähern uns einer Beschreibung der dynamischen Phänomene bei der Ellipse mit der ersten qualitativen Aussage für einen allgemeineren Fall als den von
Bahnen durch die Brennpunkte. Wir werden zunächst folgendes zeigen: Wenn
die Strecke zwischen zwei Randpunkten der Bahn und die Strecke zwischen den
beiden Brennpunkten sich nicht schneiden, schneidet auch die nächste Strecke
zu dem folgenden Randpunkt die Verbindungsstrecke zwischen den Brennpunkten nicht. Da man aufgrund des völlig symmetrischen Reflexionsgesetzes jede
Bahn umkehren kann, läßt sich unsere Beobachtung auch so formulieren: Wenn
eine Strecke der Bahn die Strecke zwischen den Brennpunkten schneidet, dann
schneidet jede Strecke zwischen zwei Randpunkten der Bahn die Brennpunktstrecke.
P2
11
00
P1 00
11
11
00
F1
F2
1
0
1
0
0 P3
1
Abbildung 8: Skizze zu Bahnen, die nicht zwischen den Brennpunkten verlaufen
Betrachten wir also drei aufeinanderfolgende Randpunkte der Bahn, nennen
wir sie P1 , P2 , P3 und nehmen wir an, die Strecke P1 P2 schneide die Brennpunktstrecke F1 F2 nicht. Da die Brennpunktstrecke nicht getroffen wird und
das Reflexionsgesetz sowohl für die Strecken P1 P2 und P2 P3 als auch für die
Strecken F1 P2 und P2 F1 gilt, ist der Winkel zwischen der Tangente und der
Strecke P1 P2 kleiner als zwischen der Tangente und F1 P2 .
Aus der Reflexionseigenschaft folgt damit, dass der Winkel, den die Strecken
F1 P2 und P2 F1 einschließen, ganz in dem Winkel zwischen P1 P2 und P2 P3
enthalten ist.
Insbesondere kann die Strecke P2 P3 die Brennpunktstrecke F1 F2 nicht schneiden. Also schneidet entweder jede Teilstrecke der Bahn die Brennpunktstrecke
oder keine.
8
Im Fall eines Billards mit kreisförmiger Bande haben wir gezeigt, dass die Dynamik durch immer wieder angewandte Rotationen stets mit dem gleichen Winkel beschrieben werden kann. Nun kann diese Beschreibung nicht mit Hilfe von
Winkeln auf Ellipsen übertragen werden. Man kann die Situation auf dem Kreis
auf eine andere Weise beschreiben, die dann eine Verallgemeinerung auf die Situation auf der Ellipse erlaubt.
Konfokale Ellipsen
Da bei dem Kreis-Billard die Winkel, mit denen die Kugeln an einem Bandenpunkt reflektiert werden, stets gleiche Größe haben, gibt es einen konzentrischen5 Kreis, so dass jede der Sekanten, entlang derer die Billardkugel rollte,
tangential an diesen Kreis ist. Wir haben diese Situation hier für einen Winkel
von 45o skizziert.
Abbildung 9: Konzentrischer Kreis, an den alle Bahn-Sekanten tangential sind
Wir möchten nun – lediglich Eigenschaften von Winkeln und Kongruenzsätze
von Dreiecken werden dafür benötigt – beweisen, dass wie beim kreisförmigen
Billard im Fall der Ellipse alle Bahnensegmente tangential an Ellipsen sind, die
dieselben Brennpunkte wie die ursprüngliche Ellipse, aber kleiner sind, m. a.
W.: die einbeschriebene Ellipse unterscheidet sich von der Billardtisch-Ellipse
nur durch die Länge des Seiles. Dazu betrachten wir eine Kugel, die vom Punkt
A0 am Rand der Ellipse aus in Bewegung gesetzt wird, und verfolgen ihren
Weg, bis sie danach zum zweiten Mal die elliptische Bande berührt. Zum ersten
Mal berührt sie die Ellipse im Punkt A1 , zum zweiten Mal in A2 . Das Ziel
besteht nun darin zu zeigen, dass es möglich ist, eine Ellipse mit denselben
Brennpunkten F1 und F2 zu finden, die die Strecken zwischen A0 und A1 sowie
zwischen A1 und A2 berührt.
Als erstes stellen wir fest, dass der Winkel zwischen der Strecke von A0 nach
A1 und der Strecke von F1 nach A1 und der Winkel zwischen der Strecke von
A2 nach A1 und der Strecke zwischen F2 und A1 gleich sind. Der Grund dafür
liegt darin, dass sowohl der Winkel zwischen der Tangente und der Strecke von
A0 nach A1 und der Winkel zwischen der Tangente und der Strecke von A1 und
A2 übereinstimmen als auch die Winkel zwischen der Tangente und der Strecke
5
ein konzentrischer Kreis mit kleinerem Radius ist einer mit demselben Mittelpunkt wie
der ursprüngliche Kreis
9
A1
A2
A0
F1
F2
von F1 bis A1 sowie von F2 bis A1 maßgleich sind. Da es sich bei dem Verlauf
von A0 über A1 nach A2 und von F1 über A1 nach F2 um mögliche Bahnen
einer Billardkugel handelt, rühren die Übereinstimmungen der o. g. Winkel vom
Reflexionsprinzip her, dass Einfallswinkel und Ausfallswinkel gleich sind.
A1
A2
A0
F1
F2
Nun finden wir uns eine konfokale Ellipse, also eine mit denselben Brennpunkten
F1 und F2 , die die Strecke von dem Punkt A0 zum Punkt A1 berührt. Wenn
man nämlich die Seillänge einer Gärtnerellipse verändert, deformiert sich die
Gestalt der Ellipse stetig. Ist die Seillänge klein, so schneiden sich die Strecke
von A0 zu A1 und die Ellipse nicht. Es gibt eine minimale Seillänge, bei der
es zum ersten Mal einen Berührpunkt B gibt. Die ist nun die Ellipse, zu der
die Strecke von A0 nach A1 tangential liegt. Die Form der Ellipse läßt übrigens
nicht zu, dass bei dieser Ellipse mehrere Berührpunkte gibt. Eine Fläche mit
einer Ellipse als Rand ist konvex: Mit zwei Punkten auf der Fläche liegt auch
die verbindende Strecke zwischen diesen Punkten auf der Strecke. Würde eine
Strecke nun genau zwei Berührpunkte haben und sonst außerhalb liegen, dann
könnte man die Ellipse auf einer (schnurgeraden) Strecke erst verlassen und
dann wieder zurückkommen.
In derselben Weise findet man eine konfokale Ellipse, die die Strecke von A1 nach
A2 in genau einem Punkt C berührt. Wir haben nun zu zeigen, dass diese beiden
Ellipsen übereinstimmen. M. a. W.: Wir müssen beweisen, dass die jeweiligen
10
F2
A1
F1
A2
C
B
F1
A0
F2
Seillängen, zum einen die Summe aus den Längen der Strecken von F1 nach B
sowie von B nach F2 und zum anderen die Summe aus den Längen der Strecken
von F1 nach C sowie von C nach F2 gleich sind: |F1 B| + |BF2 | = |F1 C| + |CF2 |.
Dazu spiegeln wir den Punkt F1 an der Strecke von A0 nach A1 und erhalten
den Punkt F1 :
F2
A1
F1
A2
A0
F1
F2
Nun werden wir zeigen, dass die Strecke von F2 nach F1 die Strecke von A0
nach A1 im Punkt B schneidet, in dem die Ellipse diese Strecke berührt. Wir
nennen den Schnittpunkt von der Geraden von F2 nach F1 mit der Geraden
durch A0 und A1 zunächst S, denn wir haben diesen Punkt anders als B enthalten, und suchen nach eine Begründung, warum S mit B übereinstimmt. Wegen
des Spiegelns sind die Strecken von F1 nach S und von F1 nach S gleich lang.
Deshalb ist das Dreieck mit dem Eckpunkten S, F1 und F1 gleichschenklig, und
die Winkel zwischen den Strecken von F1 nach S und von A0 nach S, sowie zwischen den Strecken von F1 nach S und von A0 nach S stimmen überein. Da die
Winkel zwischen den Strecken von F1 nach S und von S nach A0 sowie zwischen
F2 und S sowie zwischen S und A1 als Scheitelwinkel übereinstimmen, erfüllt
S also genau die Reflexionseigenschaft einer Ellipse mit dem Brennpunkten F1
und F2 und der Geraden durch A0 und A1 als Tangente. Der Schnittpunkt S
ist B.
11
F2
A1
F1
B
A2
C
A0
F1
F2
Der Rest ist nun einfach. Auf Grund unserer Voruntersuchungen können wir
jetzt zeigen, dass die beiden Dreiecke ∆(F1 A1 F2 ) und ∆(F1 A1 F2 ) kongruent
sind, weil nach den Spiegelungseigenschaften die Strecken F1 B und F1 B die gleiche Länge besitzen – ebenso wie die Strecken F2 A1 und A1 F2 . Unsere Betrachtungen der Winkel zeigen, dass die beiden Dreiecke ∆(F1 A1 F2 ) und ∆(F1 A1 F2 )
in A1 kongruente Winkel besitzen und deshalb nach einem Kongruenzsatz, der
auch gern mit WSW “abgekürzt wird, kongruente Dreiecke sind.
”
Insbesondere sind die Strecken F1 F2 und F1 F2 kongruent, und es folgt
|F1 B| + |BF2 | = |F1 F2 | = |F1 F2 | = |F1 C| + |CF2 |.
Und dies war zu zeigen.
Abbildung 10: Schon nach einigen Bandenberührungen läßt sich die konfokale
Ellipse erahnen, die alle Bahnen tangential berühren.
Entweder sind alle Bahnen periodisch oder keine
Mit Lichtstrahlen in Ellipsen hatten sich schon Euler und Lagrange im 18.
Jahrhundert beschäftigt. Das persönliche Schicksal eines Kriegsgefangen brachte Bewegung in diese Fragen. Der Franzose Jean Poncelet war mit Napoleon
12
im Rußlandfeldzug als Soldat in Gefangenschaft geraten, als sich Napoleon in
Richtung Waterloo aus dem Staub machte. In den Jahren von 1811 bis 1814
saß Poncelet in der russischen Stadt Rubikov in Kriegsgefangenschaft und hatte
Zeit zum Nachdenken.
Poncelet betrachtete eine Ellipse, in deren Innerem eine andere Ellipse enthalten
ist. Ausgehend von einem Strahl zwischen zwei Endpunkten der großen Ellipse
betrachtete er nun Bahnen, die immer die einbeschriebene Ellipse berühren.
Offenbar betrifft dies allgemeinere Bahnen als diejenigen, die aus Spiegelungen
hervorgehen.
Zu zwei derartigen Ellipsen bewies Poncelet dann nun folgenden Satz: Wenn
es eine periodische Bahn gibt (also eine, die an ihren Ausgangspunkt zurückkommt), dann ist jede Bahn eine periodische Bahn. Er konnte sogar zeigen, dass
jede Bahn nach der gleichen Anzahl an Bandenberührungen zurückkommt. Für
unsere Situation bedeutet dies, dass wie beim eingangs diskutierten Kreis entweder jede Bahn, deren Streckenabschnitte die einbeschriebene Ellipse tangential
berühren, periodisch durchlaufen wird oder keine.
Dichte, nicht-periodische Bahnen
Wenn es also eine periodische Bahn gibt, weiss man gleich sehr viel über die
Qualität jeder Bahn. Im Fall keiner periodischen Bahn hilft uns ein klassischer
Satz von Denjoy weiter: Denjoy zeigt, dass man in diesem Fall die Ellipse so
zu einem Kreisrand verformen kann, dass die entsprechende Abbildung von
Kreisrandpunkt zu Kreisrandpunkt einer Drehung um einen irrationalen, d. h.
nicht zu 2π kommensurablen, Winkel entspricht.
Insbesondere greift unsere Beschreibung zu Beginn über die Punkte einer irrationalen Drehung, die jedem Bahnpunkt beliebig oft beliebig nah kommt. Die
Punkte auf der Bahn liegen dicht auf dem Einheitskreis. Dies kann man auch
so ausdrücken, dass es auf der Kreislinie keinen zusammenhängenden Abschnitt
mit mehr als einem Punkt gibt, die von keiner Bahn getroffen wird.
Ein Wort zu konfokalen Hyperbeln
Abbildung 11: Bahnen durch die Brennpunktstrecke sind alle tangential an eine
konfokale Hyperbel
Was geschieht nun, wenn wir die Billardkugel so schießen, dass sie zwischen
den beiden Brennpunkten hindurch geht? Wir wissen schon, dass dann alle
Streckenabschnitte der Bahn auch durch die Brennpunktstrecke hindurchgehen.
13
Dann kann es keine konfokalen Ellipsen tangential an jeden Bahnabschnitt mehr
geben. Denn jede Bahn verliefe quer durch eine konfokale Ellipse hindurch.
Dennoch verlaufen die Bahnen geordnet weiter: Es sind nun nicht mehr Ellipsen,
sondern Hyperbeln mit denselben Brennpunkten F1 und F2 der ursprünglichen
Ellipse, an die die Bahnabschnitte tangential sind. Eine Hyperbel zwischen zwei
Brennpunkten ist die Menge aller Punkte, so dass die Differenz der Abstände zu
den beiden Brennpunkten konstant ist – nach Definition einer Ellipse ist dort
die Summe dieser Abstände konstant. Wer sich für diesen Fall interessiert kann
den Fall der Hyperbeln mit denselben Mitteln wie in unserem Fall der Ellipsen
behandeln.
Konstanten der Bewegung
Auch in dem Fall, dass es keine periodischen Bahnen zu einer Ellipse und ihrem
konfokalen Zwilling gibt und jede Bahn jedem Punkt auf dem Rand beliebig
oft beliebig nah kommt, ist die Geometrie der Bahn in der Ebene also alles
andere als willkürlich chaotisch. Es gibt eine Konstante der Bewegung: Jeder
Streckenabschnitt ist tangential an eine konfokale Ellipse bzw. Hyperbel.
Man macht sich diese Tatsache beispielsweise bei der Datenübertragung im
Glasfaserkabel zunutze: Ist ein solches Kabel von elliptischem – also vertikal zur
Ausbreitungsrichtung des Laserstrahls –, so weiß man von den Laserstrahlen,
die man z. B. auf der einen Seite des Atlantik losgesendet hat, besser, wie man
sie auf der anderen Seite wieder entlang der konfokalen Ellipse einfangen kann.
14