Lösungen der Aufgaben - pythagoras-club

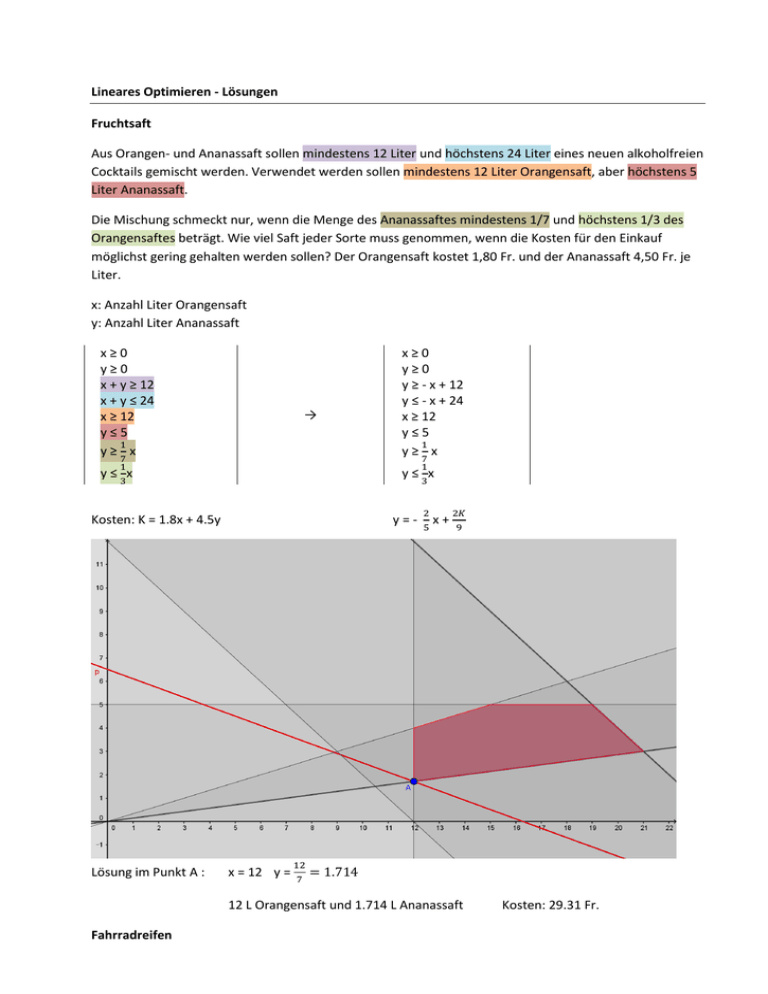
Lineares Optimieren - Lösungen
Fruchtsaft
Aus Orangen- und Ananassaft sollen mindestens 12 Liter und höchstens 24 Liter eines neuen alkoholfreien
Cocktails gemischt werden. Verwendet werden sollen mindestens 12 Liter Orangensaft, aber höchstens 5
Liter Ananassaft.
Die Mischung schmeckt nur, wenn die Menge des Ananassaftes mindestens 1/7 und höchstens 1/3 des
Orangensaftes beträgt. Wie viel Saft jeder Sorte muss genommen, wenn die Kosten für den Einkauf
möglichst gering gehalten werden sollen? Der Orangensaft kostet 1,80 Fr. und der Ananassaft 4,50 Fr. je
Liter.
x: Anzahl Liter Orangensaft
y: Anzahl Liter Ananassaft
x≥0
y≥0
x + y ≥ 12
x + y ≤ 24
x ≥ 12
y≤5
1
y≥7x
→
1
1
y ≤ 3x
y ≤ 3x
Kosten: K = 1.8x + 4.5y
Lösung im Punkt A :
x≥0
y≥0
y ≥ - x + 12
y ≤ - x + 24
x ≥ 12
y≤5
1
y≥7x
y=-
x = 12 y =
12
7
2
5
x+
2𝐾
9
= 1.714
12 L Orangensaft und 1.714 L Ananassaft
Fahrradreifen
Kosten: 29.31 Fr.
Eine Fabrik stellt zwei Sorten Fahrradreifen her. Pro Tag können insgesamt maximal 200 Reifen produziert
werden. Vom Typ A dürfen nicht mehr als 150 Stück angefertigt werden. Vom Typ B sollten höchstens
doppelt so viel wie vom Typ A produziert werden.
Der Reingewinn beim Typ A beträgt Fr. 2.- pro Stück, beim Typ B Fr. 3.- pro Stück.
Wie viele Reifen von jeder Sorte sollen produziert werden, wenn der Reingewinn möglichst gross sein
soll?
x: Anzahl Fahrradreifen Typ A
y: Anzahl Fahrradreifen Typ B
x≥0
y≥0
x + y  200
x ≤ 150
y ≤ 2x
→
Gewinn: G = 2x + 3y
Lösung im Punkt A :
x≥0
y≥0
y  - x +200
x ≤ 150
y ≤ 2x
y=-
2
3
x+
𝐺
3
x = 67 y = 133
67 Fahrradreifen Typ A und 133 Fahrradreifen Typ B
Der Reingewinn beträgt 533 Fr.
Teemischung
Ein Teehändler will eine aus zwei Sorten bestehende Teemischung herstellen, die er zu einem Preis von 40
Fr. je Kilogramm verkaufen möchte. Zur Verfügung stehen 15 kg der ersten Sorte, die zu einem Preis von
48 Fr. je Kilogramm verkauft werden kann. Mindestens 6 Kilogramm dieser Sorte sind für die Mischung
bestimmt. Von der zweiten Sorte sollen maximal 60% in der Mischung enthalten sein, von der er 12 kg auf
Lager hat. Diese Sorte kann zum Kilogrammpreis von 36 Fr. verkauft werden.
Wie ist zu mischen, damit beim Verkauf der Mischung sowie der Restmengen der beiden Sorten ein
möglichst grosser Gewinn erwirtschaftet wird?
x: Anzahl kg teurere Teesorte in der Mischung
y: Anzahl kg billigere Teesorte in der Mischung
x≥0
y≥0
x ≤ 15
x≥6
y ≤ 0.6(x+y)
y ≤ 12
→
Preis: P = 40(x+y) + 48(15 – x) + 36(12 – y)
Lösung im Punkt A :
x=6
y=9
x≥0
y≥0
x ≤ 15
x≥6
y ≤ 1.5x
y ≤ 12
𝑃
y = 2 x + 4 – 288
Verkaufspreis = 40 x 15 + 9 x 48 + 3 x 36 = 1140 Fr.
Autos
Ein Automobilwerk stellt zwei Wagentypen A und B her. Vom Typ A können täglich maximal 600 Stück
fertiggestellt werden, vom Typ B maximal 300 Stück, wegen Mangel an Personal jedoch nicht mehr als
750 Stück insgesamt.
Der Reingewinn für einen Wagen vom Typ A beträgt durchschnittlich Fr. 2400.-, für einen Wagen vom Typ
B Fr. 3600.-.
a)
Wie viele Wagen werden täglich von jedem Typ produziert, wenn der Reingewinn maximal werden
soll? Wie gross ist dieser Reingewinn?
b)
Wie ändert sich die Sachlage, wenn sich herausstellt, dass vom Typ B höchstens halb so viele Wagen
verkauft werden können wie vom Typ A? Wie gross ist nun der Reingewinn?
x: Anzahl Wagen Typ A
y: Anzahl Wagen Typ B
x≥0
y≥0
x ≤ 600
y ≤ 300
x + y ≤ 750
→
1
y≤2x
Reingewinn: G = 2400x + 3600y
a) Lösung im Punkt A x = 450 y = 300
450 Wagen Typ A und 300 Wagen Typ B
Gewinn G = 2400450 + 3600300 =2'160'000 Fr.
x≥0
y≥0
x ≤ 600
y ≤ 300
y ≤ – x +750
1
y≤2x
2
𝐺
y = − 3 x + 3600
b) Lösung im Punkt A x = 500
y = 250
500 Wagen Typ A und 250 Wagen Typ B
Gewinn G = 2400500 + 3600250 =2'100'000 Fr.
Zwei Zahlen
Zwei Zahlen x und y sollen die folgenden 4 Bedingungen erfüllen:
y+6
≤ 3x
2y – x ≥ 0
x+y
≥6
2y + x ≤ 16
Stelle die Lösungsmenge graphisch dar und beantworte durch ablesen aus der Zeichnung die folgenden
Fragen:
a) Welches ist für y der grösste mögliche Wert?
b) Welches ist für x der kleinste mögliche Wert?
Die 4 Bedingungen:
y  3x – 6
y≥-x+6
1
y x
2
1
2
y– x+8
a) Lösung im Punkt A: y = 6
b) Lösung im Punkt B: x = 3