Effektivwert - antriebstechnik.fh
Werbung

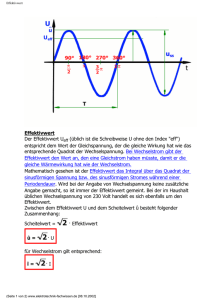
Effektivwert Mess- und Sensortechnik HTA Biel Effektivwert Es ist eigentlich nicht ganz einzusehen, weshalb der Effektivwert in der Elektrotechnik eine derart dominierende Bedeutung hat. Vermutlich wollte man damit erreichen, dass - wie beim Gleichstrom - das Produkt aus Strom und Spannung der mittleren Leistung entspricht. Messtechnisch viel einfacher zu erfassen wäre aber der Spitzen- oder Scheitelwert. Den (wahren oder wirklichen) Effektivwert können nämlich für beliebige Kurvenformen nur relativ teure und aufwendige Instrumente genau messen. Die kostengünstigen Dreheisenmessgeräte eignen sich nur für tiefe Frequenzen (bis einige hundert Hertz) und niedrige Crestfaktoren. Zudem weisen sie einen recht grossen Eigenverbrauch auf, wodurch sie für die Elektronik von geringer Bedeutung sind. Drehspulinstrumente mit Gleichrichter eignen sich wiederum nur für sinusförmige Signale. Gebräuchliche Verfahren zur Messung des Effektivwertes sind Geräte mit Thermoumformer und elektronische Wandler. Beim Thermowandler wird die Wärmewirkung des Messstromes an einem Widerstand gemessen. Auf diese Weise lassen sich recht präzise von der Kurvenform und von der Frequenz unabhängige Geräte bauen. Sie sind aber durch das Verfahren bedingt ziemlich träge und werden bei Ueberlastung leicht zerstört. Sogenannte True RMS Instrumente 'berechnen' den Effektivwert auf Grund der Definition des Effektivwertes. Sie sind aber recht teuer und erlauben nur genaue Messungen bis zu einem spezifizierten maximalen Crestfaktor (2..5). In der folgenden Laborübung sollen am Beispiel eines Lichtreglers nichtsinusförmige Signalformen gemessen und diskutiert werden. Wichtiger Hinweis: Sie arbeiten am 220V Wechselspannungsnetz. Aus messtechnischen Gründen muss zudem die Schutzerde, die gewöhnlich mit dem KO-Gehäuse verbunden ist, unterbrochen werden! Arbeiten Sie deshalb mit Bedacht und vermeiden Sie blanke Anschlüsse, damit Berührungen mit spannungsführenden Teilen ausgeschlossen werden können. Vermeiden Sie unter allen Umständen, dass der Masseanschluss der Sonde mit der Netzphase verbunden wird! Kontrollieren Sie Ihre Schaltung genau, bevor Sie das Netz einschalten! Kontrollieren Sie mit Messgeräten und Phasenprüfer ob nicht fälschlich die Phase mit dem KO-Gehäuse verbunden ist, bevor Sie metallische Teile (KO) berühren! Ueberlegen und bestimmen Sie genau, welcher Anschluss der Phase und welcher dem Nulleiter entspricht. Verwenden Sie eine 100:1 KO-Sonde, um Netzspannungen auf dem KO darzustellen. AC und DC True RMS Die meisten True RMS anzeigenden Instrumente messen nur den AC-Anteil (AC True RMS) zwischen AC und DC True RMS gilt die folgende Beziehung: X DC EFF = X 2 DC + X 2 AC EFF X EFF Formfaktor kf = Crestfaktor X ks = X EFF X ^ Laborübung Seite 1 Effektivwert Mess- und Sensortechnik HTA Biel Drehspulinstrumente mit Gleichrichter Bei Drehspulinstrumenten mit (Vollweg-) Gleichrichter kann der Effektivwert näherungsweise wie folgt bestimmt werden: X EFF Signal = X EFF abgelesen 1.11 ⋅ k f Signal Lichtregler In einem Lichtregler wird mittels eines elektronischen Schalters (Thyristor resp. Triac) nur während eines einstellbaren Teils einer Periode Spannung an die Lampe gelegt. Der Winkel αz wird Zündwinkel genannt und der Winkel bis 180° wird als Stromflusswinkel bezeichnet. Mit den üblichen Lichtreglern kann der Zündwinkel etwa im Bereich von 20° bis 160° verändert werden. Der Effektivwert bei Phasenanschnittsteuerung Auf Grund der Definition des Effektivwertes ergibt sich bei einer Phasenanschnittsteuerung folgender vom Zündwinkel αz abhängiger Effektivwert: 2π U EFF = 1 2 U(ϕ ) dϕ = ∫ 2π 0 π π − α z + sinα z ⋅ cosα z Û2 2 sin ϕ ⋅ d ϕ = Û ⋅ π α∫z 2π Der Betragsmittelwert bei Phasenanschnittsteuerung U = Laborübung 1 2π 2π ∫ 0 U(ϕ ) dϕ = π Û Û sinϕ ⋅ dϕ = (1 + cos α z ) ∫ π αz π Seite 2 Effektivwert Mess- und Sensortechnik HTA Biel Der Formfaktor bei Phasenanschnittsteuerung Der Formfaktor ergibt sich aus dem Verhältnis des jeweiligen Effektivwertes zum Betragsmittelwert: kf = X EFF (α z ) X (α z ) = π[(π − α z ) + sinα z ⋅ cosα z ] 2 ⋅ (1 + cosα z ) Der Crestfaktor bei Phasenanschnittsteuerung Der Crestfaktor ergibt sich aus dem jeweiligen Verhältnis des Spitzenwertes zum Effektivwert. Bei Zündwinkeln unter 90° ist der Spitzenwert gleich dem Spitzenwert des sinusförmigen Signals. Bei grösseren Zündwinkeln hingegen muss der jeweilige Spitzenwert errechnet werden. 2π π ; α ≤ z ^ 2 (π - α z ) + sinα z ⋅ cosα z X ks = = X EFF 2π π ; αz > sinα z ⋅ (π - α z ) + sinα z ⋅ cosα z 2 Messanordnung Mit der folgenden Messanordnung soll die veränderliche Spannung an einer Glühlampe gemessen werden: Geräteliste: ! ! ! ! ! ! ! ! ! Variac, Lampe 60 W Lichtregler KO mit 100:1 Sonde Dreheiseninstrument Siemens VAeff Multizet Drehspulinstrument mit Gleichrichter Metravo 4S BBC Goerz Metrawatt Digitalvoltmeter MA 2D BBC Goerz Metrawatt (zeigt etwa den Betragsmittelwert an) Digitalinstrument Philips PM 2518 (AC-TRUE-RMS) Digitalmultimeter Hewlett Packard 34401A (AC-TRUE-RMS) Handmultimeter ROLINE 187 (TRUE-RMS) Mit dem Variac wird die Netzspannung während der Messung auf 220 V geregelt. Laborübung Seite 3 Effektivwert Mess- und Sensortechnik HTA Biel Aufgaben 1. Studieren Sie die Messanordnung genau und beachten Sie den Hinweis über die Messung am 220 V Netz. Stellen Sie genau fest, welcher Netzanschluss dem Null-Leiter und welcher der Phase entspricht. 2. Betrachten Sie mit dem KO und einer 100:1 Sonde (Abgleich nicht vergessen) die 220V Netzspannung. Sie werden feststellen, dass die Netzspannug namentlich in Biel ziemliche Verzerrungen aufweist. Dies ist vor allem eine Folge der in der Stadt verteilten Gleichrichter für die Busse der Verkehrsbetriebe. W ichtig: Der Erdstift des KO-Netzsteckers darf nicht geerdet sein! 3. Lesen Sie in 30°Schritten des Zündwinkels die Anzeigen der verschiedenen Instrumente ab, wobei Sie mit dem Variac die Eingangsspannung konstant halten. Ueberprüfen Sie zu Beginn ohne Lichtregler, indem Sie alle Instrumente parallel schalten, ob die Anzeigen übereinstimmen. Ermitteln Sie durch Messung und Rechnung die folgenden W erte: U1 αz U21 U22 U23 U24 U25 kf(αz) ks(αz) U24* U25* 0û αz min 30û 60û 90û 120û 150û αz max U 24 * und U 25 * sind die korrigierten Effektivwerte U eff Signal ≈ U eff abgelesen 1.11 ⋅ k f Signal 4. Vergleichen und diskutieren Sie die erhaltenen W erte. 5. Beweisen Sie durch Anwendung der Definition des Effektivwertes, dass die Beziehung zwischen DC- und AC-True-RMS für eine mit einer Gleichspannung überlagerten W echselspannung u(t) = U DC + u ac (t) richtig ist, wobei Sie u ac (t) = U p sin(ωt) setzen können. Laborübung Seite 4