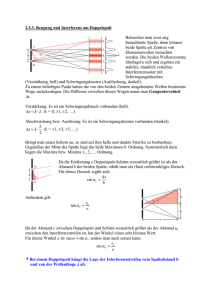
AUFBAU EINES QUANTENRADIERERS UND DER EINSATZ IM

JOHANNES GUTENBERG-UNIVERSITÄT MAINZ
INSTITUT FÜR PHYSIK
AUFBAU EINES QUANTENRADIERERS
UND
DER EINSATZ IM SCHÜLERLABOR
Wissenschaftliche Prüfungsarbeit im Rahmen der
Ersten Staatsprüfung für das Lehramt an Gymnasien
eingereicht von
Alexander Leuck
im September 2007
Gutachter:
Prof. Dr. Th. Trefzger
Prof. Dr. H. – G. Sander
„Wer über die Quantentheorie nicht entsetzt ist, der
hat sie nicht verstanden“ (Niels Bohr)
Inhaltsverzeichnis
1. Einleitung .........................................................................................1
2. Historische Entwicklung der Quantenphysik ................................3
2.1 Geschichte des Lichts..................................................................................... 3
2.2 Die Geburtsstunde der Quantenmechanik.................................................... 12
2.2.1 Die spektrale Verteilungsfunktion eines schwarzen Körpers.................. 13
2.3 EINSTEINs Deutung des Photoeffekts ............................................................ 16
2.4 Der Wellencharakter von Teilchen................................................................ 18
2.5 Das DAVISSON – GERMER – Experiment......................................................... 19
2.6 Die Wellenmechanik von ERWIN SCHRÖDINGER ............................................. 20
2.7 Die Wahrscheinlichkeitsinterpretation der Wellenfunktion ............................ 22
3. Experimente des Schülerlabors ...................................................24
3.1 Der mathematische Formalismus der Quantenmechanik ............................. 24
3.2 Das Doppelspalt – Experiment ..................................................................... 27
3.2.1 Das TAYLOR – Experiment ...................................................................... 28
3.2.2 Das JÖNSSON – Experiment.................................................................... 30
3.2.3 Das Komplementaritätsprinzip ............................................................... 34
3.3 Das MACH – ZEHNDER – Interferometer......................................................... 36
3.3.1 Der Aufbau ............................................................................................. 36
3.3.2 Interferenz an einem idealisierten MACH – ZEHNDER – Interferometer.... 37
3.3.2.1 Licht hoher Intensität ....................................................................... 37
3.3.2.2 Licht geringer Intensität ................................................................... 39
3.4 Die ‚wechselwirkungsfreie Messung’ ............................................................ 41
3.5 Interpretation der Quantenmechanik............................................................. 43
3.5.1 Die Kopenhagener Interpretation der Quantenmechanik ....................... 44
3.5.2 Die BOHMsche Interpretation der Quantenmechanik .............................. 45
4. Der Quantenradierer......................................................................49
4.1 Interferenz an einem realen MACH – ZEHNDER – Interferometer.................... 49
4.2 Polarisation von Photonen ............................................................................ 52
4.3 Die Funktionsweise des Quantenradierers ................................................... 53
4.4 Der Aufbau des Quantenradierers als Realexperiment ................................ 56
4.5 Die Justage des Quantenradierers ............................................................... 62
I
4.6 Komplementarität am realen Quantenradierer.............................................. 65
5. Planung und Durchführung des Schülerlabors...........................67
5.1 Vorbemerkung .............................................................................................. 67
5.2 Bezug zum Lehrplan ..................................................................................... 68
5.3 Das Konzept des Schülerlabors.................................................................... 71
5.4 Das Doppelspalt – Experiment als didaktischer Alleskönner ........................ 72
5.5. Erster Tag des Schülerlabors ...................................................................... 73
5.5.1 Der einführende Vortrag......................................................................... 73
5.5.2 Die Experimente des Stationenlernens .................................................. 75
5.5.2.1 Der Photoeffekt................................................................................ 76
5.5.2.2 Das Doppelspalt – Experiment ........................................................ 80
5.5.2.3 Die Elektronenbeugungsröhre ......................................................... 83
5.6 Zweiter Tag des Schülerlabors ..................................................................... 89
5.6.1 Der einführende Vortrag......................................................................... 89
5.6.2 Die Experimente der Gruppenphase ...................................................... 91
5.6.2.1 Der Computer als Experimentiertisch .............................................. 92
5.6.2.2 Das MACH – ZEHNDER – Interferometer............................................ 96
5.6.2.3 Die Kopenhagener Interpretation der Quantenmechanik ................ 97
5.6.2.4 Die BOHMsche Interpretation der Quantenmechanik ....................... 99
5.7 Durchführung und zeitlicher Rahmen des Schülerlabors .............................. 99
5.8 Evaluation und Auswertung des Schülerlabors........................................... 109
6. Zusammenfassung ......................................................................116
7. Anhang .........................................................................................118
Anhang A: Evaluationsbogen und Auswertung der Evaluation ......................... 118
Anhang B: Bauteile des Quantenradierers mit Preisinformation ....................... 127
Anhang C: Verwendete Materialien auf beiliegender CD.................................. 128
8. Referenzen ...................................................................................129
8.1 Literatur....................................................................................................... 129
8.2 Simulationen ............................................................................................... 133
8.3 Abbildungen................................................................................................ 134
8.4 Portraits ...................................................................................................... 136
Abbildungsverzeichnis ...................................................................137
Tabellenverzeichnis ........................................................................139
II
Danksagung.....................................................................................140
Erklärung..........................................................................................141
Impressum .......................................................................................142
III
1. Einleitung
Die Quantenphysik wurde 1900 durch Einführen des Energiequantums der Größe
E=h
von MAX PLANCK eingeleitet (Abschnitt 2.2), wobei h = 6,6260693(11) 10 -34 Js
[Dem05] ist und die Dimension einer Wirkung trägt. Licht der Frequenz
aus Energiequanten, sogenannten Photonen, der Größe E = h
besteht
. Die Photonen
können als ‚Teilchen’ interpretiert werden. Bis zum Einführen des Energiequantums
von MAX PLANCK wurde Licht durch eine elektromagnetische Welle beschrieben.
Des Weiteren wurde nachgewiesen, dass auch Materie durch eine Welle
beschrieben werden muss, wodurch der sogenannte Welle – Teilchen – Dualismus
entstand. Der Welle – Teilchen – Dualismus zeigt sich vor allem am Doppelspalt –
Experiment. Trifft Licht hoher Intensität auf einen Doppelspalt, so zeigt sich auf
einem hinter dem Doppelspalt befindlichen Schirm das bekannte Interferenzmuster
(Abschnitt 2.1), welches sich durch das Wellenmodell des Lichts erklären lässt.
Verringert man die Intensität des Lichts und schießt einzelne Photonen auf den
Doppelspalt, so bildet sich nach einer gewissen Belichtungszeit das bekannte
Interferenzmuster aus den stochastisch verteilten Einzeltreffern heraus (Abschnitt
3.2.1). Für ein Ensemble (Menge identisch präparierter (z.B. gleiche Frequenz)
Photonen,
die
sich
gegenseitig
nicht
beeinflussen)
kann
man
in
der
Quantenmechanik vorhersagen treffen, und so das Interferenzmuster für Licht
hoher Intensität berechnen. Aber man ist nicht in der Lage die einzelnen
Photonentreffer auf dem Schirm vorherzusagen.
Somit musste das deterministische Weltbild der Physiker des 19. Jahrhunderts
durch die Quantenphysik aufgegeben werden. Niels Bohr drückte sein Entsetzen
über die Quantenphysik im Zitat zu Beginn dieser Arbeit aus.
Heute ist die Quantenphysik nicht mehr aus unserem Alltag wegzudenken. Viele
technische
Entwicklungen
wie
Laser
und
Computer
basieren
auf
der
Quantenphysik. So hält auch die Quantenphysik immer mehr Einzug in
populärwissenschaftliche Literatur [Zei07 und Zei05], in der interessante Aspekte
wie das Phänomen der Verschränkung, die Quantenteleportation und die
Quantenkryptographie dargestellt werden. Neben der Aktualität der Quantenphysik
gibt es in ihr auch heute noch offene Fragen, die zur Zeit nicht beantwortet werden
können.
1
Dadurch bietet vor allem die Thematik der Quantenphysik einen hervorragenden
Einblick in ein modernes, kontrovers diskutiertes Themengebiet der Physik, das
neben einem neuen physikalischen Weltbild in der physikalischen Grundausbildung
nicht
fehlen
soll
[Mül05].
Aus
diesem
Grund
wird
im
Rahmen
dieser
Staatsexamensarbeit ein Schülerlabor zur Quantenphysik entwickelt. In dem
Schülerlabor werden die Charakteristika (Abschnitt 5.4) der Quantenphysik mit Hilfe
verschiedener
Experimente
(Doppelspalt
–
Experiment,
Photoeffekt,
Elektronenbeugung und MACH – ZEHNDER – Interferometer) erarbeitet. Da sich das
Schülerlabor durch Realexperimente auszeichnen soll, wird ein Quantenradierer
aufgebaut,
um
die
Komplementarität
–
ein
fundamentales
Prinzip
der
Quantenphysik – nicht nur mit Hilfe von Simulationen, sondern auch am realen
Experiment zu beobachten. Ein Quantenradierer ist ein MACH – ZEHNDER –
Interferometer, das mit drei Polarisationsfiltern aufgebaut wird. Um einen Einblick in
die
offenen
Fragen
der
Quantenphysik
zu
geben,
werden
zwei
Interpretationsrichtungen (Abschnitt 3.5) der Quantenphysik im Schülerlabor
erarbeitet. Durch die Aktualität der Quantenphysik und durch die offenen Fragen,
die dort existieren, soll das Interesse der Schüler1 an der Physik verstärkt bzw.
geweckt werden.
Zu Beginn der vorliegenden Examensarbeit wird die historische Entwicklung der
Quantenmechanik thematisiert, um die Physik, die im Schülerlabor verwendet wird,
zu verstehen. Nach der historischen Einführung in die Quantenmechanik werden
die wichtigsten Experimente des Schülerlabors beschrieben. Anschließend werden
die Funktionsweise und der Aufbau des Quantenradierers als Realexperiment
beschrieben um die Beobachtungen zu verstehen. Durch den detailliert
beschriebenen Aufbau des Quantenradierers wird ein eventueller Nachbau des
Experiments in der Schule ermöglicht, um den Quantenradierer auch in Schulen
einsetzen zu können. Danach werden das Konzept und die Durchführung des
Schülerlabors beschrieben. Um die Eindrücke und Kommentare der Schüler zu
diesem Schülerlabor darzustellen, wird eine Evaluation des Schülerlabors
durchgeführt. In der Zusammenfassung wird zusätzlich ein Ausblick für eine
mögliche Themenergänzung des Schülerlabors angeführt.
1
Schüler beinhaltet sowohl den Schüler als auch die Schülerin.
2
2. Historische Entwicklung der Quantenphysik
Im Folgenden wird ein Überblick über die Geschichte des Lichts gegeben,
beginnend bei NEWTON und HUYGENS, bis hin zu MAX PLANCKs Theorie der
Strahlung eines schwarzen Körpers Anfang des 20. Jahrhunderts. Ab diesem
Zeitpunkt
beginnt die
Entwicklung der Quantenmechanik, die
wichtigsten
Experimente und Erkenntnisse der Quantenmechanik werden im Folgenden
behandelt. Als Abschluss der geschichtlichen Entwicklung der Quantenmechanik
wird der Formalismus der Wellenfunktion thematisiert.
2.1 Geschichte des Lichts
Korpuskulartheorie des Lichts
Für ISAAC NEWTON (1634 – 1727) war Licht eine Fortbewegung von
Lichtteilchen bzw. Korpuskeln. Mit der Korpuskulartheorie des Lichts
konnte er unter anderem das Brechungsgesetz des Lichts in seinem
Werk Opticks erklären [Ne52]. Er musste allerdings annehmen, dass
sich das Licht in einem Medium wie Glas oder Wasser schneller
NEWTON
ausbreitet als in Luft. Aus heutiger Sicht weiß man natürlich, dass diese Annahme
falsch ist. Die Überprüfung dieser Annahme ließ allerdings noch anderthalb
Jahrhunderte auf sich warten [Si90].
Wellentheorie des Lichts
Im Gegensatz zu ISAAC NEWTON hat CHRISTIAAN HUYGENS (1629 –
1695) eine Wellentheorie des Lichts aufgestellt, welche er 1690 in
seiner
Abhandlung
über
das
Licht
Tractatus
de
Lumine
veröffentlichte [Hu64]. Er stellte sich die Lichtausbreitung ähnlich wie
HUYGENS
3
die Ausbreitung von Schall vor. Für die Erklärung des Brechungsgesetzes musste
bei der HUYGENSschen Theorie die Annahme gemacht werden dass sich das Licht
in einem Medium wie Glas oder Wasser, langsamer ausbreitet als in Luft. Aber wie
in NEWTONs Fall, konnte die Annahme zu dieser Zeit noch nicht überprüft werden,
so dass es zwei konkurrierende Theorien gab, die dieselben Vorhersagen machten
[Si90].
Das Prinzip der Interferenz am Doppelspalt
Bei der Entwicklung der Lichttheorie gelang erstmals THOMAS YOUNG
(1773 – 1829), Anfang des 19. Jahrhunderts, der Durchbruch. Er
benutzte ein neues Prinzip, die Interferenz, und konnte so die
meisten zu jener Zeit bekannten Phänomene erklären. Auch wenn
YOUNG zunächst dachte, Licht sei eine longitudinale Welle (analog
YOUNG
zum Schall) so waren seine Erklärungen doch sehr zutreffend [Kip90]. Da das
Prinzip der Interferenz die Wellentheorie des Lichts entscheidend untermauerte,
wird im Folgenden die Vorstellung von YOUNG zur Interferenz angeführt. YOUNG
ging von folgender Annahme aus:
„Nehmen wir an, ein Zug gleichartiger Wellen auf der Oberfläche eines stehendes
Gewässers pflanze sich mit konstanter Geschwindigkeit fort und gerate in einen engen
Kanal, der aus dem Gewässer herausführt. Nehmen wir weiter an, eine ähnliche
Ursache rege einen weiteren, ähnlichen Wellenzug an, der
mit derselben
Geschwindigkeit und gleichzeitig zum selben Kanal gelangt, wie der erste. Es wird
dann keiner der beiden Wellenzüge den anderen vernichten, vielmehr ihre Wirkung
vereint zur Geltung kommen: treten sie dermaßen in den Kanal ein, dass die
Wellenberge des einen Zuges mit denen des anderen zusammenfallen, so ergibt sich
ein Wellenzug mit höheren Bergen; wenn hingegen die Wellenberge des einen Zuges
auf die Wellentäler des anderen zu liegen kommen, so füllen sie diese letzteren genau
auf und die Oberfläche des Wassers bleibt glatt. Ich wenigstens sehe keine andere
Möglichkeit, weder aufgrund der Theorie, noch anhand der Versuche. Nun behaupte
ich, dass es zu ebensolchen Effekten kommt, wenn auf dieselbe Art zwei Wellenzügen
des Lichts vermischt werden, und ich will dies das allgemeine Gesetz der Interferenz
nennen.“
[Si90, S. 355].
4
YOUNG verdeutlichte seine Interferenz in unten stehender Abbildung (Abbildung 1).
In Punkt A und B werden simultan zwei Steine ins Wasser geworfen. Von diesen
zwei Punkten gehen Wellenzüge aus, die sich verstärken oder auch auslöschen
können. YOUNG bemerkte auch, dass die Minima und Maxima der interferierenden
Wellenzüge auf Hyperbeln liegen [Kip90].
Abb. 1: Interferenz zweier Wasserwellen
YOUNG übertrug als Erster die Vorstellung der Interferenz bei mechanischen Wellen
in die Optik und konnte so die Interferenz von Licht am Doppelspalt erklären
[Kip90]. Ihm war auch die Kohärenzbedingung (räumliche Kohärenz: die
Wellenzüge müssen länger sein als der Gangunterschied zweier Wellen) für das
Auftreten der Interferenz bewusst [Si90]. Im Wesentlichen spiegelt die heutige
Darstellung der Interferenz am Doppelspalt in physikalischen Lehrbüchern die
Gedanken YOUNGs wider, so dass an dieser Stelle die Lehrbuchdarstellung
verwendet werden kann. Wenn kohärentes monochromatisches Licht auf einen
Doppelspalt fällt, so entsteht auf einem Schirm hinter dem Doppelspalt ein Muster
aus hellen und dunklen Streifen (Abbildung 2).
Abb. 2: Interferenzmuster am Doppelspalt
5
Abb. 3: Gangunterschiede
Von Spalt A und Spalt B (Abbildung 3) gehen nach dem HUYGENschen
Elementarwellenprinzip zwei kohärente Wellen aus. Diese beiden Wellen haben
einen Gangunterschied von
s = d sin , wenn sie sich in der Richtung
wieder
vereinigen, unter der Annahme, dass die Entfernung Schirm – Doppelspalt im
Vergleich zum Spaltabstand d sehr groß ist. Im Punkt P erhält man im Fall eines
Gangunterschieds von
s=n
Helligkeit und im Fall von
Dunkelheit, wobei n = 0, 1, 2, 3, … und
s=
2n + 1
2
die Wellenlänge des Lichts ist [Ge99].
Aber es gelang weder YOUNG noch anderen Physikern, wie z.B. AUGUSTIN JEAN
FRESNEL, mit Hilfe der longitudinalen Wellen die Polarisationserscheinungen zu
erklären [Hop67].
6
Licht als transversale Welle
ÉTIENNE LOUIS MALUS (1775 – 1812) hatte das Phänomen der
Polarisation im Jahre 1808 an einem Doppelspat beobachtet
[Hop67]. AUGUSTIN JEAN FRESNEL (1788 – 1827) hatte 1820 eine
vollständig
theoretische
Beschreibung
der
Phänomene
der
Polarisation gegeben. Bei ihm begegnete man auch zum ersten Mal
einer Darstellungsform für Wellen: a sin
(t -
x
)+
c
FRESNEL
. Außerdem hatte er auch
linear und zirkular polarisierte Wellen mathematisch beschrieben. Das Phänomen
der Polarisation konnte nicht durch die Annahme, dass Licht eine longitudinale
Welle ist, erklärt werden. Licht musste also eine transversale Welle sein, womit die
Korpuskulartheorie von NEWTON endgültig ausgeschlossen werden konnte [Si90]. In
der
heutigen
Lehrbuchdarstellung
Schwingungsebene
des
elektrischen
wird
Feldes
die
um
Polarisation
die
durch
die
Ausbreitungsrichtung
beschrieben.
Abb. 4: Polarisation des Lichts
7
r
Bei einer linear polarisierten Welle zeigt der Vektor E 0 einer Welle
r r
E = E0
ei(
t - kz)
(2.1)
immer in die gleiche Richtung orthogonal zu êz (Abbildung 4 b)), d.h.
r
E 0 = E 0x eˆ x + E 0y eˆ y
(2.2)
lässt sich in zwei orthogonale Basisvektoren zerlegen (Abbildung 4 a)). Beide
Komponenten
E x = E 0x
ei(
t-kz)
(2.3)
E y = E 0y
ei(
t-kz)
(2.4)
schwingen in Phase [Dem99].
Um aus unpolarisiertem Licht, wie es von einer herkömmlichen Lichtquelle emittiert
wird, linear polarisiertes Licht zu erzeugen, wird ein Polarisationsfilter benutzt. Der
Polarisationsfilter lässt nur Licht einer Schwingungsrichtung durch (Abbildung 5).
Abb. 5: Polarisationsfilter
Hierbei wird ausgenutzt dass die Schwingungsebenen des Lichts, die nicht mit der
Durchlassrichtung (Transmissionsachse) übereinstimmen, absorbiert werden.
8
Abb. 6: Polarisator und Analysator
Durch den Polarisator P1 wird das Licht linear polarisiert und trifft auf einen zweiten
Polarisator P2, den Analysator, dessen Transmissionsachse um den Winkel
zur
ursprünglichen Transmissionsachse von Polarisator P1 verkippt ist (Abbildung 6).
r
Das elektrische Feld zwischen den Polarisatoren sei E . Der Analysator lässt nur
r
r
die Komponente von E durch, die aus der orthogonalen Projektion von E auf die
Transmissionsachse entsteht. Somit beträgt die durchgelassene Komponente nach
dem Analysator: E x = E
E y' = E sin (
cos (
).
Die absorbierte Komponente beträgt somit:
r
) . Die Intensität des Lichts ist proportional zu E 2 , wodurch nach dem
Analysator die Intensität des Lichts I = I0
cos 2 (
)
beträgt [Tip00].
Licht als elektromagnetische Welle
MICHAEL FARADAY (1791 – 1867) vermutete, dass es sich bei Licht um
elektromagnetische Wellen handelt. Er war ein sehr guter Experimentator, aber es
gelang ihm weder einen experimentellen noch einen theoretischen Beweis für diese
9
Vermutung
zu
erbringen.
Der
theoretische
Beweis
für
die
Wesensgleichheit von Licht und einer elektromagnetischen Welle
stammt
von
dem
größten
theoretischen
Physiker
des
19.
Jahrhunderts, JAMES CLERK MAXWELL (1831 – 1879) [Si90]. Er stellte
MAXWELL
vier Grundgleichungen für die Elektrodynamik auf, die alle
Informationen über die magnetischen und elektrischen Felder beinhalten:
r
div E =
(2.5)
r
div B = 0
(2.6)
r
r
B
rot E = t
(2.7)
r
r
rot B = µ0 j + µ0
0
r
E
.
t
(2.8)
Aus den MAXWELLschen Gleichungen (2.7) und (2.8) für den quellenfreien Raum
lassen sich Wellengleichungen der Form
r
r
E
1 2E
= 2 2
x2
c t
2
(2.9)
ableiten, wobei die Ausbreitungsgeschwindigkeit durch
c=
1
µ0
(2.10)
0
gegeben ist. Da die Ausbreitungsgeschwindigkeit einer elektromagnetischen Welle
gleich der Lichtgeschwindigkeit ist, und es sich bei den Lösungen der
Wellengleichung (2.9) um ebene Wellen handelt, schloss MAXWELL folgerichtig,
dass das Licht eine elektromagnetische Welle ist. Bei einer elektromagnetischen
Welle stehen das Magnetfeld und das elektrische Feld senkrecht aufeinander
10
(Abbildung 7). Dieser Sachverhalt folgt auch aus den MAXWELLschen Gleichungen
[Tip00].
Abb. 7: Elektromagnetische Welle
HEINRICH HERTZ (1857 – 1894) konnte 1888 letztendlich den
experimentellen Beweis für die Wesensgleichheit von Licht und
elektromagnetischen Wellen liefern. Somit stand Ende des 19.
Jahrhunderts fest, dass es sich bei Licht um eine transversale
elektromagnetische Welle handelt. Beachtenswert ist an dieser
Stelle, dass zwei unterschiedliche Gebiete der damaligen Physik, die
HERTZ
Optik und die Elektrodynamik, die sich nebeneinander entwickelten, in eine Theorie
gefasst werden konnten [Si90].
Wechselwirkung von Licht mit Materie
HEINRICH HERTZ und sein Schüler W ILHELM HALLWACHS (1859 – 1922) entdeckten,
dass bei Bestrahlung von Materie mit Licht geladene Teilchen ausgelöst werden.
Dieser Effekt ist heute als Hallwachseffekt oder Photoeffekt bekannt. Dass es sich
bei den geladenen Teilchen um Elektronen handelt, konnte PHILIPP LENARD (1862 –
1947) um 1900 bestätigen. Er untersuchte diesen Effekt etwas genauer und fand
zum einen heraus, dass dieser Effekt nur bei Bestrahlung von hinreichend
kurzwelligem Licht auftritt, und zum anderen, dass die Geschwindigkeit der
Elektronen nur von der Frequenz des Lichts und nicht von seiner Intensität abhängt.
Auch bei Licht mit schwacher Intensität konnten Elektronen ausgelöst werden und
der Effekt trat sofort, ohne längere Beleuchtung, auf. Diese Beobachtungen
11
konnten mit dem bekannten Wellenmodell des Lichts nicht erklärt werden. Eine
Erklärung wurde erst 1905 durch ALBERT EINSTEIN mit Hilfe der Quantenphysik
gegeben, die in Abschnitt 2.3 diskutiert wird [Hun84].
2.2 Die Geburtsstunde der Quantenmechanik
Die Entwicklung der Quantenmechanik lässt sich auf den Zeitraum von 1900 bis
1927 eingrenzen. Die Physik, die diesem Zeitraum vorausging, bezeichnet man als
klassische Physik. Die klassische Physik gegen Ende des 19. Jahrhunderts lässt
sich in drei Teilgebiete gliedern [Hun84]:
•
Die Mechanik der Systeme von Massenpunkten (Physik der Materie in
Abbildung 8)
•
Die Theorie des elektromagnetischen Feldes und des Lichts (Physik des Äthers
in Abbildung 8)
•
Die Thermodynamik und die statistische Physik
Die Physik gegen Ende des 19. Jahrhunderts war in einer Endzeitstimmung und
viele Physiker, wie A. A. MICHELSON waren überzeugt, dass
„die wichtigsten Grundgesetze und Grundtatsachen der Physik [...] alle schon entdeckt
[sind]; und diese haben sich bis jetzt so fest bewährt, dass die Möglichkeit, sie wegen
neuer Entdeckungen beiseite zu schieben, außerordentlich fern zu liegen scheint [...].
Unsere künftigen Entdeckungen müssen wir in den 6. Dezimalstellen suchen.“
[Si90,
S.393].
Allerdings taten sich auch „Wolken am Himmel der Physik des 19. Jahrhunderts“
[Si90, S.393] auf, wie LORD KELVIN 1900 die Probleme der damaligen Physik in
einem Vortrag nannte. Die Wolken, also die offenen Probleme, sind in Abbildung 8
schematisch dargestellt.
12
Abb. 8: Offene Probleme
Die
offenen
Probleme
sind
durch
ein
Fragezeichen
gekennzeichnet, und die Phänomene, die sich nicht in den
Rahmen der klassischen Physik einfügen lassen, sind farbig
markiert. Im Folgenden ist allerdings nur die Strahlung schwarzer
Körper relevant, da nach der Suche einer Theorie für die Erklärung
der
Spektralverteilung
eines
schwarzen
Körpers
die
PLANCK
Quantenmechanik von MAX PLANCK (1858 – 1947) im Jahre 1900 eingeleitet wurde.
Worin die Probleme bei der Theoriefindung für die Spektralverteilung mit Hilfe der
klassischen Physik lagen, und wie die Quantenmechanik hier den entscheidenden
Durchbruch brachte, wird im folgenden Abschnitt diskutiert [Si90].
2.2.1 Die spektrale Verteilungsfunktion eines
schwarzen Körpers
Die Spektralverteilung (Abbildung 9) der Strahlung eines schwarzen Körpers konnte
nur mit Hilfe der Quantenmechanik theoretisch beschrieben werden. Man
bezeichnet als schwarzen Körper ein System, das die gesamte einfallende
Strahlung absorbiert.
13
Abb. 9: Spektralverteilung eines schwarzen Körpers
Ein schwarzer Körper lässt sich experimentell durch einen Hohlraum mit einer
kleinen Öffnung gut realisieren (Abbildung 10). Aus diesem Grund wird auch oft von
der Hohlraumstrahlung geredet, wenn man die Strahlung eines schwarzen Körpers
meint. Die Strahlung befindet sich im Hohlraum im ständigen thermischen
Gleichgewicht mit den Wänden. Die Wände emittieren und absorbieren ständig die
Strahlung.
Abb. 10: Experimentelle Realisierung eines schwarzen Körpers
Die Strahlung kann in den Hohlraum durch das Loch ein- bzw. austreten. Die
Wände werden auf einer gleichmäßigen Temperatur gehalten, die variiert werden
kann. Damit das thermische Gleichgewicht im Hohlraum durch die ein- und
austretende Strahlung so wenig wie möglich gestört wird, muss das Loch klein
gehalten werden. Die geometrische Beschaffenheit des Körpers hat keinen Einfluss
auf die Eigenschaften der Hohlraumstrahlung, diese werden lediglich durch die
Temperatur verändert. Abbildung 9 zeigt die abgestrahlte Leistung P ( , T ) eines
14
schwarzen Körpers in Abhängigkeit von der Wellenlänge für drei verschiedene
Temperaturen.
Innerhalb der klassischen Thermodynamik konnten RAYLEIGH und JEANS folgende
Spektralverteilungsfunktion P ( , T ) herleiten:
P ( ,T ) =
8 k BT
4
,
(2.11)
wobei kB die BOLTZMANN – Konstante ist.
Abb. 11: Spektrale Verteilung der Hohlraumstrahlung bei 1600 K
Das RAYLEIGH – JEANS – Gesetz ist in Abbildung 11 als gestrichelte Kurve
dargestellt, wobei die Spektralverteilungsfunktion in Abbildung 11 u( ) genannt
wird.
Vergleicht
man
Spektralverteilungsfunktion
die
(2.11)
Kurve
bei
der
RAYLEIGH
kleinen
–
Wellenlängen
JEANSschen
mit
den
experimentellen Daten in Abbildung 11, so erkennt man, dass in diesem Bereich
keine Übereinstimmung vorliegt. Die Übereinstimmung mit den experimentellen
Daten ist nur für große Wellenlängen gegeben. Im Grenzwert
experimentell bestimmte Spektralverteilung
P ( , T)
0 geht die
gegen Null, wobei die
berechnete Spektralverteilung von RAYLEIGH und JEANS gegen unendlich geht. Man
nennt dieses Resultat auch Ultraviolettkatastrophe [Tip00].
15
MAX PLANCKs Leistung war das Auffinden der Spektralverteilungsfunktion, die mit
den
experimentellen
Daten
über
dem
gesamten
Wellenlängenbereich
übereinstimmt (Abbildung 11). Bei der Herleitung seiner Spektralverteilungsfunktion
P ( ,T ) =
8 hc
1
5
e
hc
+kt
(2.12)
-1
suchte PLANCK nach einer Korrekturmöglichkeit in den klassischen Berechnungen
[Dem05]. Sein größter Erfolg war in der Annahme, dass die Energie des schwarzen
Körpers nicht als kontinuierliche Größe betrachtet werden kann, sondern dass sie
nur in kleinen Paketen, sogenannte Quanten, emittiert und absorbiert wird. Er fand
heraus, dass die Energie eines Quantums proportional zur Frequenz ist:
E=h
wobei h = 6,6260693
(2.13)
,
10-34 Js ist und die Dimension einer Wirkung trägt. Deshalb
wird h auch als PLANCKsches Wirkungsquantum bezeichnet. PLANCK war jedoch
nicht in der Lage, diese Konstante in die klassische Physik einzupassen. Die
fundamentale Bedeutung der Energiequantisierung wurde deutlich, als EINSTEIN mit
der Hilfe der Energiequantisierung den Photoeffekt erklärte [Tip00].
2.3 EINSTEINs Deutung des Photoeffekts
In Abschnitt 2.1 wurde der Photoeffekt erwähnt, welcher nicht
durch das Wellenmodell des Lichts erklärt werden konnte.
ALBERT EINSTEIN (1879 – 1955) war der Erste, dem die
Bedeutung des Quantenbegriffs über die Strahlungsformel
hinaus bewusst war. Er lieferte im Jahre 1905 in derselben
Ausgabe
der
Annalen
der
Physik,
in
der
auch
seine
EINSTEIN
Relativitätstheorie erschienen ist, eine Erklärung für den Photoeffekt. EINSTEIN
nahm an, dass Licht mit der Frequenz
aus Energiequanten der Größe h
(sog.
Photonen) besteht, und hat die Emission eines Elektrons auf die Wechselwirkung
16
mit einem Photon zurückgeführt, wobei das Elektron die Energie des Photons
aufnimmt [Si90]. Er beschrieb den Vorgang gemäß der Gleichung:
h
=
mv2
+ P,
2
(2.14)
wobei P die zu verrichtende Arbeit ist, um die Elektronen abzulösen [Hun84]. Die
Photonen besitzen analog zu klassischen Teilchen auch einen Impuls. Man kann
einem Photon gemäß der Beziehung E = mc2 zwischen Energie E und Masse m
eines Teilchens formal die Masse
m=
E
h
2 =
c
c2
(2.15)
zuordnen. Man muss allerdings beachten, dass es keine ruhenden Photonen gibt,
so dass die ‚Masse’ nicht der Ruhemasse eines klassischen Teilchens entspricht.
Somit folgt aus dem relativistischen Energieansatz
E = p 2c2 + m02 c4
mit m0 = 0 (Ruhemasse eines Photons), dass der Impuls p =
die Energie E = h
(2.16)
E
ist. Setzt man für
c
ein, so erhält man für den Impuls eines Lichtquants folgende
Beziehung:
p=
h
.
(2.17)
Man sieht, dass die Teilcheneigenschaften Masse, Energie und Impuls des Photons
nur über die Welleneigenschaften Frequenz
bzw. Wellenlänge
definiert sind
[Dem05]. Man kann sich jetzt fragen, ob dies in analoger Weise auch für Materie
zutrifft. LOUIS
DE
BROGLIE befasste sich mit dieser Fragestellung, die im nächsten
Abschnitt dargestellt wird.
17
2.4 Der Wellencharakter von Teilchen
Wie
in
Abschnitt
2.1
gezeigt
wurde,
lässt
sich
das
Interferenzmuster am Doppelspalt mit dem Wellenmodell des
Lichts erklären. Anderseits ist der Photoeffekt ein Beweis für den
Teilchencharakter des Lichts. LOUIS
DE
BROGLIE (1892 – 1987)
hatte nun folgenden Gedanken: Bei Licht wurde von vielen
Physikern (YOUNG, FRESNEL, MAXWELL, HERTZ) über sehr lange
Zeit zu sehr der Wellenaspekt in den Vordergrund gestellt, und
DE BROGLIE
der Teilchencharakter vernachlässigt, wodurch bei der Erklärung des Photoeffekts
und der Strahlung eines schwarzen Körpers Probleme auftraten. DE BROGLIE
meinte, dass man bei Teilchen wie Elektronen nicht den gleichen Fehler begehen
sollte. Nach seiner Meinung musste auch der Wellenaspekt von Teilchen betrachtet
werden. Diesen Kerngedanken führte er 1924 in seiner Doktorarbeit Recherches
sur la Théorie des Quanta [Si90] aus und kam zu dem Ergebnis, dass auch einem
Teilchen mit dem Impuls
p=m v
(2.18)
eine Wellenlänge, analog zu der Beziehung zwischen Impuls und Wellenlänge beim
Licht (Abschnitt 2.3), zugeordnet werden kann. Für ein Teilchen der Masse m, das
sich mit der Geschwindigkeit v bewegt erhält man somit:
=
Da die Materiewellen oder
DE
h
h
=
.
p
m v
(2.19)
BROGLIE – Wellen aber erst 1927 experimentell von
C.J. DAVISSON und L.H. GERMER bestätigt werden konnten, wurde er anfangs in der
Fachwelt mit seiner Theorie von manchen Physikern, wie z.B. ERWIN SCHRÖDINGER
belächelt [Si90].
18
2.5 Das DAVISSON – GERMER – Experiment
C.J. DAVISSON und L.H. GERMER entdeckten 1927 beim Beschuss eines
Nickelkristalls mit Elektronen Beugungs- und Interferenzeffekte von Elektronen.
Abbildung 12 zeigt den Versuchsaufbau.
Abb. 12: Versuchsaufbau des DAVISSON – GERMER – Experiments
DAVISSON
und
GERMER
beobachteten
die
Maxima
und
Minima
der
Intensitätsverteilung der gestreuten Elektronen in Abhängigkeit des Streuwinkels. In
Abbildung 13 erkennt man ein typisches Beugungsmuster mit einem ausgeprägten
Maximum unter einem Winkel von 50°. Die Lage des Intensitätsmaximums hängt
von der Materiewellenlänge der Elektronen und den Gitterabständen im
Nickelkristall ab.
19
Abb. 13: Winkelabhängigkeit der Intensität der gestreuten Elektronen
Somit konnten DAVISSON und GERMER die Hypothese der Materiewellen von
DE
BROGLIE überprüfen, da die Wellenlänge der Elektronen in der Größenordnung der
Gitterabstände im Kristall liegt. Durch Variieren der Elektronenenergie und der
Winkelbestimmung der Maxima und Minima konnten DAVISSON und GERMER die
Wellenlänge
der
Elektronen
Übereinstimmung mit dem von
DE
bestimmen.
So
erzielten
sie
eine
gute
BROGLIE errechneten Wert für die Materiewellen
von Elektronen [Tip00]. Da bis zu dieser Stelle lediglich Ergebnisse und deren
Erklärungen ohne eine allumfassende, fundierte Theorie der Quantenmechanik
behandelt wurde, wird in den folgenden Abschnitten ein Formalismus der
Quantenmechanik vorgestellt.
2.6 Die Wellenmechanik von ERWIN SCHRÖDINGER
Vergleicht
man
die
Gesetze
der
geometrischen
Optik
mit
denen
der
Elektronenoptik, so stellt man fest, dass die Bahnen eines Lichtstrahls und die
Bahnen eines Elektrons in einem elektrischen Feld in engem Zusammenhang
stehen. Wenn ein bestimmter Zusammenhang zwischen dem ortsabhängigen
optischen Brechungsindex und dem ortsabhängigen Potential des elektrischen
20
Feldes erfüllt ist, fallen die Bahn eines Elektrons und eines Lichtstrahls zusammen
(Abbildung 14).
Abb. 14: Analogie zwischen klassischer Mechanik und Strahlenoptik
Für kleine Wellenlängen ist die Strahlenoptik ein Grenzfall der
Wellenoptik, in analoger Weise erwartet man, dass sich die
klassische Mechanik als Grenzfall einer neuen Mechanik entpuppt,
der ‚Wellenmechanik’. ERWIN SCHRÖDINGER (1887 – 1961) konnte
1926
über
die
oben
erwähnte
Analogiebetrachtung
eine
SCHRÖDINGER
Wellengleichung aufstellen, die das Verhalten von Elektronen als Welle und als
Teilchen beschreibt [Si90]. Die allgemeine zeitabhängige, dreidimensionale
Schrödingergleichung (Wellengleichung) für ein Teilchen der Masse m lautet
-h 2
2m
r
r
r
( r, t ) + E ( r, t ) ( r, t ) = ih
pot
r
( r, t ) ,
t
(2.20)
21
wobei h =
h
bedeutet und Epot die potentielle Energie des Teilchens ist [Dem05].
2
Eine Lösung der eindimensionalen Schrödingergleichung für ein freies, kräftefreies
Teilchen ist die Exponentialform einer harmonischen Wellenfunktion
( x, t ) = A
e(
i kx- t )
(2.21)
mit A als Konstante. Die Wellenfunktionen, die die Schrödingergleichung erfüllen,
müssen nicht notwendigerweise reell sein, wie Gleichung (2.21) zeigt. Offensichtlich
kann man solch einer Funktion keine reale Existenz zuschreiben und deshalb auch
nicht direkt messen [Tip03]. Es bedarf also einer Interpretation der Wellenfunktion,
die für die Realität relevant ist. MAX BORN entwickelte eine Interpretation, die im
nächsten Abschnitt vorgestellt wird.
2.7 Die Wahrscheinlichkeitsinterpretation der
Wellenfunktion
Die Verknüpfung der Schrödingergleichung mit Messergebnissen geht auf MAX
BORN (1882 – 1970) zurück. Einem Quantenobjekt, z.B. einem Elektron, kann im
Allgemeinen
kein
wohldefinierter
Ort
zugeordnet
werden,
lediglich
Wahrscheinlichkeitsaussagen sind möglich. Die Wahrscheinlichkeitsdichte ein
Quantenobjekt an einem Ort x zu finden wird P(x) genannt. Ein Beispiel für solch
eine Wahrscheinlichkeitsdichte ist die Intensitätsverteilung beim Doppelspalt
(Abbildung 2). Ziel quantenmechanischer Berechnungen ist das Auffinden der
Wahrscheinlichkeitsdichte, da diese reell ist. Die Wahrscheinlichkeitsdichte
berechnet man mit Hilfe der Wellenfunktion
P(x) =
Somit
wird
aus
der
komplexen
2
(x) .
Wellenfunktion
(2.22)
eine
reelle,
messbare
Wahrscheinlichkeitsdichte. Für die Wahrscheinlichkeit, ein Teilchen im Intervall dx
zu finden, setzte BORN an:
22
P(x, t)dx =
( x, t )
2
dx .
(2.23)
Man muss sich allerdings bewusst sein, dass die Wellenfunktion sich stets auf ein
Ensemble von Quantenobjekten bezieht. Unter einem Ensemble versteht man eine
Menge von identisch präparierten Quantenobjekten, die sich gegenseitig nicht
beeinflussen. Somit löst sich der Welle – Teilchen – Dualismus auf, da die
Wellenfunktion die gleichen Eigenschaften wie eine klassische Welle besitzt und so
die Interferenzeffekte erklärt werden können. Die Lokalisation der Teilchen wird
durch das Betragsquadrat der Wellenfunktion nach MAX BORN gegeben [Tip03].
23
3. Experimente des Schülerlabors
In
diesem
Kapitel
wird
der
Formalismus
der
Wellenfunktion
am
Doppelspaltexperiment und einem alternativen Doppelspaltexperiment, dem MACH
– ZEHNDER – Interferometer, verdeutlicht. Diese beiden Versuchsaufbauten bilden
die experimentelle Grundlage des Schülerlabors. Beide Experimente bieten ein
didaktisches Potential (Abschnitt 5.4) zur Verdeutlichung der Wesenszüge, die die
Quantenphysik charakterisieren. Um den Formalismus anwenden zu können,
bedarf es einiger mathematischer Operationen, wobei die wichtigsten in Abschnitt
3.1 aufgezählt werden. Anschließend wird der Formalismus auf den Doppelspalt
und
das
MACH
–
ZEHNDER
–
Interferometer
angewendet,
um
die
Versuchsergebnisse auch quantitativ zu beschreiben.
3.1 Der mathematische Formalismus der
Quantenmechanik
In der Quantenmechanik betrachtet man (reine) Zustände eines Systems. Die
Zustände werden durch Strahlen in einem separablen, komplexen Hilbertraum
beschrieben. Ein (komplex –) eindimensionaler, linearer Teilraum entspricht genau
einem Strahl. Diese Strahlen werden meist durch einen Vektor
repräsentiert, der
in solch einem Teilraum liegt. Dieser Vektor wird oft auf eins normiert, da sich somit
eine Vereinfachung der Notation ergibt. Unterscheiden sich Vektoren nur um einen
komplexen Faktor oder um Einheitsvektoren (die sich nur um eine Phase
unterscheiden), so repräsentieren die Vektoren denselben physikalischen Zustand.
Im diesem Kapitel wird die Notation von DIRAC benutzt, so dass Vektoren in einem
Hilbertraum durch sogenannte ‚kets’ gekennzeichnet werden:
. Vektoren aus
dem dualen Hilbertraum werden durch sogenannte ‚bras’ gekennzeichnet:
.
Daher wird diese Notation auch oft als ‚bra – ket’ Schreibweise bezeichnet.
24
Nach dem Satz von RIESZ [Heu06] ist der Hilbertraum H isomorph zu seinem
H ein eindeutiges
Dualraum H’ und es gibt zu jedem f
f(
)=
H , so dass gilt:
.
(3.1)
Auf dem Hilbertraum existiert ein Skalarprodukt
RIESZschen Satzes gibt es zu jedem ‚ket’
(
,
),
und wegen des
ein eindeutiges ‚bra’
im
Dualraum, so dass für das Skalarprodukt
(
,
)
(3.2)
geschrieben werden darf. Das Skalarprodukt wird im Folgenden noch wichtig sein
[Fil04].
Die Notwendigkeit ist nun eine Verbindung des mathematischen Formalismus mit
der Physik, insbesondere die Verbindung des mathematischen Formalismus mit
den Ergebnissen physikalischer Experimente. Im Folgenden wird ein ‚Kochrezept’
der Quantenmechanik vorgestellt, das sich aus der Kopenhagener Interpretation
der Quantenmechanik ergibt. An späterer Stelle wird nochmals gesondert auf die
Kopenhagener Interpretation eingegangen. Folgende Axiome sind wortgetreu aus
dem Skript zur Vorlesung Grundlagen und Probleme der Quantenmechanik von
THOMAS FILK [Fil04] entnommen:
1. (Reine) physikalische Zustände werden durch eindimensionale Teilräume
eines separablen Hilbert – Raums dargestellt. Ein normierter Vektor
dieses Teilraums kann als Repräsentant dieses Zustands dienen.
2. Die Observable an einem physikalischen System werden durch die
selbstadjungierten Operatoren des Hilbert – Raums dargestellt. Orts – und
Impulsoperatoren erfüllen dabei folgende Bedingung:
[Q, P] = h I .
i
(3.3)
25
3. Das Spektrum eines selbstadjungierten Operators entspricht den möglichen
Messwerten einer Messung der zugehörigen Observablen an dem System.
4. Die Wahrscheinlichkeit, bei einer Messung der Observablen zu einem
den Messwert
Operator A im Zustand
mit zugehörigem Eigenvektor
zu finden, ist gleich
2
5. Die
ungestörte
.
Zeitentwicklung
(3.4)
eines
abgeschlossenen
quantenmechanischen Systems wird durch die Schrödingergleichung
-
i d
h dt
=H
(3.5)
beschrieben, wobei H der Energieoperator des Systems ist.
6. Nach einer Messung der Observablen A an einem physikalischen System
und dem Ergebnis
als Messwert befindet sich das physikalische System in
dem zugehörigen Eigenzustand
.
Wie wir ein physikalisches System in den mathematischen Formalismus zu
übertragen haben wird durch Axiom 1 und 2 vorgegeben. Die physikalische
Interpretation von Resultaten im mathematischen Formalismus wird durch Axiom 3
und 4 vorgegeben. Axiom 5 und 6 repräsentieren die Zeitentwicklung des
quantenmechanischen Systems. Auf dieser Grundlage ist es nun möglich den
Formalismus am Doppelspalt und am MACH – ZEHNDER – Interferometer
anzuwenden.
26
3.2 Das Doppelspalt – Experiment
Die Lichtquantenhypothese von EINSTEIN konnte den Photoeffekt erklären (siehe
Abschnitt 2.3), allerdings führte dies zu einem neuen Problem: Ist Licht mit einem
Wellenmodell oder mit einem Teilchenmodell zu beschreiben? Die Physiker vor
1905 beschrieben das Licht durch eine elektromagnetische Welle (Abschnitt 2.1),
und hatten somit große Probleme mit der Korpuskulartheorie des Lichts. Das
Interferenzmuster bzw. die Intensitätsverteilung des Doppelspalt – Experiments mit
Licht hoher Intensität (Abschnitt 2.1) konnte durch das Wellenmodell erklärt werden.
GEOFFREY I. TAYLOR (1886 – 1975) verschärfte 1908 den Welle – Teilchen –
Dualismus, indem er sich die Frage stellte: Was wird beobachtet wenn man
einzelne Photonen durch einen Doppelspalt schickt? Würde das Interferenzmuster
verschwinden, und kann man daraus schließen, dass sich die Photonen
gegenseitig beeinflusst haben? Oder würde die Summe aller nacheinander durch
den Doppelspalt getretenen Photonen ein Interferenzmuster erzeugen? Diese
Fragen wurden von TAYLOR 1908 experimentell untersucht [Le02].
27
3.2.1 Das TAYLOR – Experiment
TAYLOR untersuchte die Beugung von Licht an einer Nadelspitze. Der Schirm wurde
von ihm durch eine Photoplatte ersetzt, um die Treffer der Photonen nachzuweisen.
TAYLOR verringerte die Intensität des Lichts, so dass sich im Mittel nur noch ein
Photon zwischen Nadelspitze und Schirm befand.
Quelle
Doppelspalt
Schirm
Abb. 15: Versuchsaufbau zum Doppelspalt – Experiment
Um ein geeignetes Ergebnis zu erhalten, musste TAYLOR die Photoplatte allerdings
mehrere Monate belichten. An Stelle einer Nadelspitze wird im Folgenden ein
Doppelspalt (Abbildung 15) verwendet, wobei die Ergebnisse übereinstimmen.
Das experimentelle Ergebnis des TAYLOR – Experiments ist verblüffend. Nach
kurzer Belichtungszeit sieht man lediglich stochastisch verteilte Einzeltreffer der
Photonen, wie in Abbildung 16 (a) dargestellt ist, wodurch sich eine körnige Struktur
ergibt. Dauert die Belichtung allerdings sehr lange, wie in Abbildung 16 (b), erkennt
man, dass sich das bekannte Interferenzmuster, aus der körnigen Struktur,
herausbildet.
28
Abb. 16: Allmählicher Aufbau des Interferenzmusters aus einzelnen Treffern
Ist es möglich, den Ort eines einzelnen Photons auf dem Schirm vorherzusagen?
Die Antwort ist nein, denn für Einzelereignisse lassen sich in der Quantenmechanik
keine Vorhersagen machen, lediglich für ein Ensemble (Abschnitt 2.7) von identisch
präparierten Quantenobjekten (z.B. Photonen der gleichen Frequenz) ist eine
Wahrscheinlichkeitsaussage über den Ort des Auftreffens möglich. Somit muss die
Intensitätsverteilung (Abbildung 16 (c)) des Doppelspalt – Experiments bei Licht
hoher Intensität als Wahrscheinlichkeitsdichte umgedeutet werden. Da Materie
nach
DE
BROGLIE auch eine Wellenlänge zugeordnet werden kann, könnte man das
Doppelspalt – Experiment auch mit Teilchen wie Elektronen durchführen, und
beobachten, ob ein Interferenzmuster wie im Falle des TAYLOR – Experiments
entsteht [Mül00].
29
3.2.2 Das JÖNSSON – Experiment
CLAUS JÖNSSON führte 1960 das Doppelspalt – Experiment mit Elektronen durch.
Bevor die Ergebnisse dieses Experiments und seine Bedeutung für die
Wissenschaft aufgezeigt werden, wird das Doppelspalt – Experiment mit
klassischen Teilchen (z.B. Kugeln) betrachtet, um die Unterschiede zwischen
klassischen Teilchen und Quantenobjekten hervorzuheben.
Abb. 17: Doppelspalt – Experiment mit Kugeln
Betrachtet wird der Aufbau in Abbildung 17 (a). Aus einer Kanone werden
nacheinander Kugeln auf einen Doppelspalt geschossen. Die Kugeln werden von
einem Detektor registriert. Der Detektor bewegt sich entlang der x – Achse und
misst
die
Wahrscheinlichkeit
für
das
Ankommen
einer
Kugel.
Die
Wahrscheinlichkeit wird somit als Funktion von x aufgezeichnet. Als Ergebnis erhält
man die Kurve in Abbildung 17 (c). In der Zeichnung wird die Wahrscheinlichkeit
nach rechts aufgetragen und x in vertikaler Richtung, so dass die x – Achse zur
Abbildung des Apparates passt. Da die Kugeln entweder durch Spalt 1 oder Spalt 2
gekommen sein können, wird die Wahrscheinlichkeitsverteilung P12 genannt. Es ist
nicht überraschend, dass P12 zur Mitte hin groß wird, aber es ist verwunderlich,
warum gerade bei x = 0 die Wahrscheinlichkeitsverteilung ihren Maximalwert
besitzt. Um diesen Sachverhalt zu verstehen, wird das Experiment wiederholt und
einmal Spalt 2 und einmal Spalt 1 abgedeckt. Die Wahrscheinlichkeitsverteilung für
30
den Fall, dass Spalt 2 abgedeckt ist und die Kugeln nur durch Spalt 1 gehen
können, ist in Abbildung 17 (b) mit P1 gekennzeichnet. Man sieht, dass der
Maximalwert von P1 an der x – Position auftritt, die auf gerader Linie mit Spalt 1
liegt. Wenn Spalt 1 abgedeckt wird erhält man die symmetrische Kurve P2. P2
spiegelt somit die Wahrscheinlichkeitsverteilung der Kugeln wider, die durch Spalt 2
getreten sind. Vergleicht man die Wahrscheinlichkeitsverteilungen der Teile (b) und
(c) der Abbildung 17 findet man als wichtiges Ergebnis:
P12 = P1 + P2.
(3.6)
Dies bedeutet, dass die Wahrscheinlichkeiten einfach addiert werden müssen. Die
Wahrscheinlichkeit
bei
zwei
geöffneten
Spalten
ist
die
Summe
der
Wahrscheinlichkeiten bei je einem geöffneten Spalt [Fey71].
Analog zu dem oben beschriebenen Doppelspalt – Experiment mit Kugeln kann
man auch Elektronen benutzen, da es sich bei Elektronen auch um Teilchen
handelt. Es stellt sich die Frage, ob bei Quantenobjekten, wie Elektronen, eine
ähnliche Beobachtung wie bei klassischen Teilchen (Kugeln) auftritt.
Abb. 18: Doppelspalt – Experiment mit Elektronen
31
In der Physik ist es äußerst wichtig, solche Gedankenexperimente wie das
Doppelspalt – Experiment mit Elektronen auch zu überprüfen, da die beste Theorie
ohne Experiment nicht überprüfbar ist. 1960 hat CLAUS JÖNSSON als Erster das
Doppelspalt – Experiment mit Elektronen durchgeführt (Abbildung 18 (a)). Das
JÖNSSON – Experiment ist in einer Umfrage der Zeitschrift ‚Physics World’ zum
schönsten physikalischen Experiment aller Zeiten gewählt worden [Ph02]. JÖNSSON
beobachtete die Wahrscheinlichkeitsverteilung P12, die in Abbildung 18 (c)
dargestellt ist.
Elektronen sind Teilchen und sie kommen immer als ‚Ganzes’ im Detektor an. Aus
diesem Grund muss unser Elektron entweder durch Spalt 1 oder Spalt 2
hindurchgegangen sein. Analog zum Doppelspalt – Experiment mit Kugeln wird
wieder ein Spalt abgedeckt und die Wahrscheinlichkeitsverteilung beobachtet. Die
Wahrscheinlichkeitsverteilung, wenn Spalt 1 offen und Spalt 2 geschlossen ist, ist in
Abbildung 18 (b) dargestellt und wird wieder mit P1 bezeichnet. P2 ist die
Wahrscheinlichkeitsverteilung wenn Spalt 2 offen und Spalt 1 geschlossen ist. Die
Addition beider Wahrscheinlichkeitsverteilungen P1 und P2 ergibt offenbar nicht die
Wahrscheinlichkeitsverteilung P12, wie dies im Doppelspalt – Experiment mit Kugeln
der Fall war (3.6). Was ist schief gegangen? [Fey71].
Unsere Annahme, dass die Elektronen entweder durch Spalt 1 oder Spalt 2 gehen,
muss falsch gewesen sein. Aber wie kann die Wahrscheinlichkeitsverteilung P12
erklärt werden?
Das Interferenzmuster kann mit Hilfe des Superpositionsprinzips erklärt werden. Die
Elektronen, die aus der Quelle treten, befinden sich im Zustand
Q
. Der
Doppelspalt dient in diesem Fall als Filter, der einen Teil der Elektronen absorbiert.
Ein gewisser Anteil kann durch Spalt 1 bzw. Spalt 2 treten. Der Doppelspalt
projiziert aus der Wellenfunktion
Spalt 1) und
2
zwei Teilzustände:
Q
1
(Elektron tritt durch
(Elektron tritt durch Spalt 2) heraus. Hinter dem Doppelspalt kann
der Zustand des Systems Elektron als Superposition (Überlagerung) geschrieben
werden:
=
1
2
(
1
+
2
).
(3.7)
32
An einem bestimmten Punkt x auf dem Schirm wird das Elektron im Zustand x
gemessen. Nach Axiom 4 in Abschnitt 3.1 ist die Wahrscheinlichkeit dafür durch
x
2
=
(
1
x
2
2
1
2
+ x
+
2
2
x x
1
+
1
x x
2
)
(3.8)
gegeben. Die ersten beiden Terme entsprechen den Wahrscheinlichkeiten, dass
ein Elektron durch Spalt 1 geht, wenn Spalt 2 geschlossen ist, und dass ein
Elektron durch Spalt 2 geht, wenn Spalt 1 geschlossen ist. Die letzten beiden
Terme sind für die Interferenz verantwortlich (Interferenzterm). Sind sie positiv, so
kann die Gesamtwahrscheinlichkeit (P12) größer werden als die Summe der beiden
Teilwahrscheinlichkeiten (P1 und P2). Sind die Interferenzterme allerdings negativ,
so kann die Wahrscheinlichkeit sogar Null werden, wodurch die Minima in der
Wahrscheinlichkeitsverteilung P12 erklärt werden. Somit führt die Überlagerung der
beiden Anteile der Wellenfunktion zu den charakteristischen Interferenzmustern in
der Intensität [Fil04].
FEYNMAN
stellt
folgende
Regel
für
das
Eintreten
von
Interferenz
bei
Quantenobjekten auf:
„Wenn ein Ereignis auf mehrere verschiedene Weisen auftreten kann, ist die
Wahrscheinlichkeitsamplitude
für
das
Wahrscheinlichkeitsamplituden jeder
Interferenz.“ [Fey
Ereignis
die
einzeln betrachteten
Summe
Möglichkeit. Es
der
gibt
71].
Die Wahrscheinlichkeitsamplituden sind im Wesentlichen durch die oben erwähnten
Wellenfunktionen
x
1
und
x
2
gegeben.
Das
Betragsquadrat
der
Wahrscheinlichkeitsamplituden ist proportional zur Wahrscheinlichkeit ein Teilchen
am Punkt x anzutreffen. Die Superposition von Zuständen ist ein typisches Merkmal
der Quantenmechanik. Solche Superpositionen sind klassisch nicht möglich. In der
Quantenmechanik ist es nicht die Unkenntnis, welcher Zustand herrscht, sondern
es liegen tatsächlich beide Zustände vor, wie das Interferenzmuster beweist [Fil04].
Die oben erwähnte Behauptung, dass ein Elektron entweder durch Spalt 1 oder
Spalt 2 gegangen sein muss, war nicht haltbar, da sonst kein Interferenzmuster
33
entstanden wäre. Im nächsten Abschnitt wird ein Versuch diskutiert, der die
Folgerung, dass die ursprüngliche Behauptung falsch ist, überprüfen soll.
3.2.3 Das Komplementaritätsprinzip
Mit einer Lichtquelle kann auf einfache Weise eine Ortsmessung am Doppelspalt
vorgenommen werden. Dadurch lässt sich überprüfen, durch welchen Spalt ein
Elektron gegangen ist. Die Lichtquelle bestrahlt den Bereich hinter dem Doppelspalt
mit Photonen. Das Elektron macht sich im ‚Scheinwerferlicht’ hinter dem
Doppelspalt durch einen Lichtblitz bemerkbar (Abbildung 19 (a)).
Abb. 19: Ortsmessung am Doppelspalt
Allerdings hat dieses Experiment auch einen Nachteil. Das Licht muss wegen der
Proportionalität von Auflösungsvermögen und Kehrwert der Wellenlänge eine
gewisse Mindestenergie besitzen, damit das Elektron eindeutig hinter einem der
Spalten nachgewiesen werden kann. Eine Bedingung für den eindeutigen Nachweis
ist, dass der Abstand der beiden Spalte kleiner sein muss als die Wellenlänge des
Photons [Fil04].
Bei Durchführung des Experiments verschwindet das Interferenzmuster und man
erhält die Wahrscheinlichkeitsverteilung P’12 in Abbildung 19 (c). Diese Verteilung
ist aus dem Doppelspalt – Experiment mit Kugeln bekannt. Unterscheidet man die
Treffer im Detektor in der Art, dass man den Spalt, durch den die Elektronen
34
geflogen sind, notiert, so erhält man für die Elektronen die durch Spalt 1 gegangen
sind die Wahrscheinlichkeitsverteilung P’1, und für die Elektronen die durch Spalt 2
gegangen sind die Wahrscheinlichkeitsverteilung P’2 (Abbildung 19 (b)). Die
resultierende
Wahrscheinlichkeitsverteilung
setzt
sich
wieder
aus
den
Wahrscheinlichkeitsverteilungen der Einzelspalte zusammen [Fey71]:
P’12 = P’1 + P’2.
(3.9)
Das Elektron fliegt bei dieser Messanordnung tatsächlich nur durch einen Spalt.
Aber offensichtlich wurde das System durch die Beobachtung des Elektrons so
wesentlich verändert, dass die Resultate völlig anders ausfallen.
Schwächt man den Eingriff ab, in dem man die Lichtintensität reduziert, wird nicht
mehr jedes Elektron als Lichtblitz wahrgenommen. Je schwächer die Lichtintensität
ist, desto weniger Elektronen werden durch einen Lichtblitz sichtbar. Statt der
Lichtintensität kann man auch die Wellenlänge vergrößern. Die Energie der
Lichtquelle wird dadurch ebenfalls kleiner. Aber da das Auflösungsvermögen
umgekehrt proportional zur Wellenlänge ist, wird der Lichtblitz breiter, so dass keine
eindeutige Entscheidung getroffen werden kann durch welchen Spalt das Elektron
gegangen ist. Das Ergebnis ist wieder das Interferenzmuster, da man nicht in der
Lage ist, den Spalt, durch den das Elektron gegangen ist, eindeutig festzustellen
[Fil04]. Dies ist ein weiterer Wesenszug der Quantenmechanik. Man bezeichnet
diesen Wesenszug nach NIELS BOHR als Komplementaritätsprinzip, welches besagt:
„ ‚Welcher – Weg’ – Information und Interferenzmuster schließen sich aus“ [Küb02,
S. 41]. Die ‚Welcher – Weg’ – Information bezeichnet in der Literatur die Information
über die Realisierung der klassisch denkbaren Möglichkeit, obwohl von einem Weg
im klassischen Sinne keine Rede sein kann. Deshalb wird ‚Welcher – Weg’ in
einfache Anführungszeichen gesetzt [Küb02].
Somit kann am Doppelspalt – Experiment eine Reihe von Grundprinzipien der
Quantenmechanik aufgezeigt werden. Eine alternative Experimentieranordnung
ähnlich zum Doppelspalt – Experiment ist das MACH – ZEHNDER – Interferometer,
welches ebenfalls die wichtigsten Wesenszüge enthält. Aus diesem Grund wurden
im Schülerlabor auch die Grundprinzipien der Quantenphysik am MACH – ZEHNDER
– Interferometer erarbeitet (Abschnitt 5.6.2.2), welches im folgenden Abschnitt
vorgestellt wird.
35
3.3 Das MACH – ZEHNDER – Interferometer
Im Folgenden wird ein MACH – ZEHNDER – Interferometer betrachtet. Zuerst wird der
prinzipielle Aufbau erläutert und die experimentellen Ergebnisse werden mit Hilfe
des Formalismus der Wellenfunktion erklärt. Anschließend wird aufgezeigt, wie an
einem MACH – ZEHNDER – Interferometer das Prinzip der ‚wechselwirkungsfreien
Messung’ verdeutlicht werden kann.
3.3.1 Der Aufbau
Ein MACH – ZEHNDER – Interferometer (Abbildung 20) besteht aus zwei idealen
Strahlteilern (HS1 und HS2) und zwei idealen Spiegeln (S1 und S2). Die Strahlteiler
und die Spiegel bilden einen Winkel von 45° mit dem einflaufenden Lichtstrahl aus
der Quelle (Q). Der Lichtstrahl wird am ersten Strahlteiler HS1 zu 50% transmittiert
und zu 50% reflektiert (50:50 Strahlteiler). Die beiden Teilstrahlen laufen
unterschiedliche Wege (W1 und W2), bis sie wieder am zweiten Strahlteiler (HS2)
zusammengeführt werden. Man erhält auf Grund der Reflexion an einem
Strahlteiler verschiedene Gangunterschiede für die Detektoren (D1 und D2)
[Dem99].
Abb. 20: Das MACH – ZEHNDER – Interferometer
36
3.3.2 Interferenz an einem idealisierten
MACH – ZEHNDER – Interferometer
3.3.2.1 Licht hoher Intensität
Bei einem Strahlteiler tritt zwischen dem transmittierten Lichtstrahl und dem
reflektierten Lichtstrahl eine Phasenverschiebung auf. Beträgt der Winkel zwischen
den beiden Strahlen 90° (Abbildung 20), so beträgt diese Phasenverschiebung
gerade
4
. Diese Phasenverschiebung führt zu unterschiedlichen Interferenzen in
den Detektoren (D1 und D2) [Fil04].
Betrachtet wird der Lichtweg zu Detektor 1 (D1):
Weg 1 (W1): - HS1:Transmission
Gangunterschied 0
- S1: Reflexion
Gangunterschied
- HS2: Reflexion
Gangunterschied
- Summe aller Gangunterschiede:
4
3
4
Weg 2 (W2): - HS1:Reflexion
Gangunterschied
- S2: Reflexion
Gangunterschied
- HS2: Transmission
2
4
2
Gangunterschied 0
- Summe aller Gangunterschiede:
3
4
Für Detektor 1 (D1) erhält man einen relativen Gangunterschied beider Lichtwege
W1 und W2 von ;+ =
W2
-
W1
=
3
4
-
3
4
= 0 . Dies bedeutet, dass man
konstruktive Interferenz am Detektor 1 vorfindet.
37
Es gibt nun zwei Argumente für eine destruktive Interferenz im Detektor 2: Durch
die konstruktive Interferenz am Detektor 1 bleibt keine Lichtintensität mehr für
Detektor 2, also muss hier destruktive Interferenz auftreten. Man kann aber analog
zu obiger Rechnung auch für Detektor 2 die relativen Gangunterschiede
berechnen.
Betrachtet wird der Lichtweg zu Detektor 2 (D2):
Gangunterschied 0
Weg 1 (W1): - HS1:Transmission
- S1: Reflexion
Gangunterschied
2
Gangunterschied 0
- HS2: Transmission
- Summe aller Gangunterschiede:
2
Weg 2 (W2): - HS1:Reflexion
Gangunterschied
- S2: Reflexion
Gangunterschied
- HS2: Reflexion
Gangunterschied
4
2
4
- Summe aller Gangunterschiede:
Für Detektor 2 (D2) erhält man einen relativen Gangunterschied beider Lichtwege
W1 und W2 von
;+ =
W2
-
W1
= -
2
=
2
. Dies bedeutet, dass man
destruktive Interferenz am Detektor 1 vorfindet [Fil04].
Führt man den Versuch mit einzelnen Photonen durch, so kann die Beschreibung
des Lichts nicht mehr auf dem oben beschriebenen klassischen Weg vollzogen
werden. Der Formalismus des Zustands muss wieder benutzt werden.
38
3.3.2.2 Licht geringer Intensität
Für einzelne Photonen, die durch ein MACH – ZEHNDER – Interferometer (Abbildung
20) hindurch
geschickt
werden, muss eine andere,
quantenmechanische
Beschreibung benutzt werden, die im Wesentlichen auf [Fag05 und Old03] basiert.
Zuerst soll jedoch erwähnt werden, dass sich ein einzelnes Photon nicht an einem
Strahlteiler aufteilt, sondern immer als ‚Ganzes’ entweder reflektiert oder
transmittiert wird. Ein Photon, das von der Quelle emittiert wird und in das MACH –
ZEHNDER – Interferometer eintritt, besitzt den Zustand
. Betrachtet wird
zunächst Detektor 2.
Zuerst wird die Möglichkeit betrachtet, dass das Photon über Weg 2 (W2) zum
Detektor 2 gelangt. Am Strahlteiler HS1 wird das Photon reflektiert und besitzt den
neuen Zustand
1
2
e
i
,
2
(3.10)
da bei der Reflexion am Strahlteiler eine Phasenverschiebung von
durch den Exponentialterm e
i
2
auftritt, die
ausgedrückt wird. Da das Photon am Strahlteiler mit
2
einer Wahrscheinlichkeit von 50% reflektiert wird, ergibt sich der Faktor
Reflexion am Spiegel S2 bedeutet eine Phasenverschiebung von
1
2
. Die
, wodurch der
neue Zustand durch
1
2
i
e e
i
2
=
1
2
e
i
3
2
(3.11)
beschrieben wird. Eine weitere Reflexion am Strahlteiler HS2 bedeutet wieder eine
Phasenverschiebung von
2
. Für den endgültigen Zustand am Detektor D2 folgt:
39
1
1
2
2
i
e e
2
i
3
2
=
1 i2
e
2
1
2
=
.
(3.12)
Für den oberen Weg W1 tritt nur am Spiegel S1 eine Phasenverschiebung von
auf. Somit erhält man als Zustand
1 i
e
2
=!
1
2
.
(3.13)
Da beide Wegstrecken gleich lang sind, müssen weitere Phasenverschiebungen
nicht berücksichtigt werden. Beide Zustände (3.12) und (3.13) müssen wegen des
Superpositionsprinzips addiert werden, so dass für den Gesamtzustand an Detektor
2 (D2) gilt:
' 1
+ %!
& 2
1
2
$
"=0
#
.
(3.14)
Die Wahrscheinlichkeit, ein Photon im Detektor 2 zu finden, ist also Null. Betrachtet
man jetzt Detektor 1 (D1) so erhält man analog den Endzustand des Systems:
3
3
1 i2
e
2
1 i
+ e2
2
=e
i
3
2
(3.15)
.
Die Wahrscheinlichkeit, ein Photon im Zustand
im Detektor 1 (D1) zu finden,
beträgt nach Axiom 4 (3.4):
e
i
3
2
2
=e
i
3
2
2
2
=e
i
3
2
2
= 1.
(3.16)
Abschließend lässt sich sagen, dass das Photon immer in Detektor 1 (D1) und nie
in Detektor 2 (D2) registriert wird. Dieses Ergebnis stimmt mit den Berechnungen
der Interferenzen in Abschnitt 3.3.2.1 überein, wenn man die Intensitäten der
Interferenzmuster als Wahrscheinlichkeitsdichte deutet. Ein interessantes Verhalten
der Quanten zeigt sich, wenn ein Hindernis in den Strahlengang W1 oder W2
40
gestellt wird. Welche Detektoren ansprechen und welche Schlüsse man daraus
ziehen kann, wird im nächsten Abschnitt thematisiert.
3.4 Die ‚wechselwirkungsfreie Messung’
Das folgende Experiment zur ‚wechselwirkungsfreien Messung’ basiert auf einer
Idee von AVSHALOM C. ELITZUR und LEV VAIDMAN . Sie stellten sich eine Bombe vor,
die einen besonderen Sensor besitzt. Trifft ein Photon auf diesen Sensor, so
explodiert die Bombe. ELITZUR und VAIDMAN betrachten ein ganzes Arsenal solcher
Bomben, von denen jedoch die Hälfte defekt ist. Bei den defekten Bomben fehlt ein
Teil des Sensors, so dass ein auftreffendes Photon einfach durchgelassen würde.
Wie kann man testen, ob die Bombe noch intakt ist? Genau diese Frage lässt sich
mit einem MACH – ZEHNDER – Interferometer und einzelnen Photonen beantworten
[Fil04].
Abb. 21: Das Bombentest – Experiment
41
Betrachtet wird zunächst eine Schablone als Hindernis. Diese Schablone absorbiert
das Photon, falls es den Weg, in dem die Schablone positioniert ist, durchläuft
(Abbildung 21). Für das Photon gibt es zwei Möglichkeiten: Es durchläuft entweder
den abgeschirmten Weg, wird von der Schablone absorbiert und trifft auf keinen der
beiden Detektoren D oder C oder das Photon durchläuft den freien Weg und kann
am zweiten Strahlteiler reflektiert oder durchgelassen werden. In diesem Fall
messen Detektor C und D im Mittel etwa gleich viele Photonen. Ein Beweis für ein
Hindernis im Strahlengang ist also dann erbracht, wenn ein Photon in Detektor D
gelangt. Denn ist der Weg nicht versperrt, so kann auf Grund der destruktiven
Interferenz (Abschnitt 3.3.2.2) bei Detektor D nie ein Photon registriert werden. Man
hat also eine Möglichkeit gefunden ‚wechselwirkungsfrei’ ein Hindernis ausfindig zu
machen. Unter Wechselwirkung soll die strenge PAULIsche Definition verstanden
werden: „Zwei Systeme haben keine Wechselwirkung miteinander, wenn keine
Energie ausgetauscht wird.“ [Fil04, S. 88]. Wenn das Photon vom Detektor C
gemessen wird, kann keine Aussage über ein Hindernis gemacht werden. Im
folgenden Experiment ist in der Hälfte der Fälle keine Schablone vorhanden und in
der anderen Hälfte der Fälle soll eine Schablone den Weg versperren (dies
entspricht dem Fall, das die Hälfte der Bomben einen Sensor und die andere Hälfte
der Bomben keinen Sensor besitzen). Man kann nun folgende Fälle unterscheiden:
-
In 50% der Fälle fehlt die Schablone und das Photon wird immer von
Detektor C gemessen. Dieser Fall kann aber auch mit Schablone eintreten,
so dass in diesem Fall keine Aussage gemacht werden kann.
-
In 50% der Fälle ist die Schablone vorhanden, so dass in der Hälfte dieser
Fälle, also in insgesamt 25% der Fälle, die Schablone das Photon absorbiert
und keiner der Detektoren anspricht.
-
In der Hälfte der verbleibenden 25% aller Fälle registriert Detektor C das
Photon und man kann keine Aussage machen.
-
In insgesamt 12,5% aller Fälle spricht Detektor D an und man weiß, dass ein
Hindernis (Schablone oder Bombe) den Strahlengang versperrt, obwohl
keine Wechselwirkung des Photons mit dem Hindernis stattgefunden hat.
Als Gesamtstatistik erhält man folgendes Ergebnis: In 62,5% aller Fälle registriert
Detektor C das Photon und man kann keine Aussage treffen. In 25% der Fälle
42
spricht kein Detektor an, da das Photon mit dem Hindernis wechselwirkte (in
diesem Fall explodiert auch die Bombe). In den anderen 12,5% der Fälle spricht
Detektor D an und man weiß, dass ein Hindernis den Weg versperrt, ohne dass
eine Wechselwirkung stattgefunden hat. Diese Art von Messung bezeichnet man
als ‚wechselwirkungsfreie Messung’. Die Bomben können also in
1
der Fälle als
8
scharfe Bomben (mit Sensor) identifiziert werden, was auf klassischem Weg nicht
möglich ist [Fil04]. Die Quantenphysik zeigt in solchen Experimenten ihre ganze
Kuriosität. Man kann sich natürlich fragen, warum ein Quantenobjekt sich so
verhält,
wie
es
sich
verhält.
Die
verschiedenen
Interpretationen
der
Quantenmechanik versuchen eine Antwort auf diese Frage zu geben. Im nächsten
Abschnitt wird gezeigt, ob dies in eindeutiger Weise möglich ist.
3.5 Interpretation der Quantenmechanik
Der Formalismus der Wellenfunktion ist mathematisch gesehen einfach, jeder
Physiker ist mit ihm vertraut und der Formalismus liefert richtige Vorhersagen für
alle Experimente. Kurz und knapp: Die Quantenmechanik macht die genauesten
Vorhersagen aller Theorien. Trotzdem gibt es einen entscheidenden Punkt:
Solange man nicht nach dem ‚Warum’ fragt, gibt es keine Probleme. Fragt man
jedoch, warum die Welt so sein sollte, gibt FEYNMAN folgende Antwort: „Wir haben
keine Ahnung.“ [Gri06, S. 191].
Der zentrale Punkt ist also unser fehlendes Verständnis, was die Quantentheorie
wirklich bedeutet – das ist das Problem der richtigen Interpretation. JAMES HARTLE
von der Universität of California in Santa Babara bringt die Debatte um die
Interpretationen der Quantenmechanik auf den Punkt:
„Unterschiedliche Interpretationen machen dieselben Voraussagen für die Ergebnisse
von Messungen. Und das ist der Grund, warum man sich über die Interpretationen
streiten kann. Gibt es dagegen verschiedene Voraussagen, dann handelt es sich um
verschiedene Theorien, und die Diskussion um die Interpretationen ist unnötig: Wir
könnten die Theorien experimentell unterscheiden. Eine wäre richtig, die anderen
falsch.“
[BdW04, S. 46].
43
Aus
diesem
Grund
werden
im
Folgenden
zwei
sehr
unterschiedliche
Interpretationsrichtungen betrachtet: Die Kopenhagener Interpretation und die
BOHMsche Interpretation der Quantenmechanik.
3.5.1 Die Kopenhagener Interpretation der
Quantenmechanik
Die Kopenhagener Interpretation wurde von NIELS BOHR, W ERNER HEISENBERG und
WOLFGANG PAULI begründet und wahrscheinlich bekennt sich heute der Großteil der
Physiker zur Kopenhagener Interpretation. Die Kopenhagener Interpretation lässt
sich nach R. MÜLLER und S. HARTMANN in die fünf folgenden Kernaussagen
zusammenfassen, die unverändert übernommen wurden [Mül99, S.13ff]:
1. Die Unverzichtbarkeit klassischer Begriffe. Diese ergibt sich aus der
BOHR’schen Einsicht, dass uns die Darstellung aller Erfahrung immer nur in
klassischen Begriffen möglich ist.
2. Das Phänomen der Komplementarität, das sich etwa im Doppelspalt –
Experiment manifestiert.
3. Die Ganzheitlichkeit der Quantenphänomene. Diese zeigt sich z.B. im
berühmten Gedankenexperiment von ALBERT EINSTEIN, BORIS PODOLSKY und
NATHAN ROSEN und wird nicht zuletzt in BOHRs Antwort auf diese Arbeit klar
beschrieben.
4. Die Aufgabe des Determinismus. Diese drückt sich in der fundamentalen
Rolle
von
Wahrscheinlichkeiten
(BOHM’sche
Interpretation)
in
der
Quantentheorie aus. Damit hängt auch die Aufgabe des Bahnbegriffs der
klassischen
Mechanik
zusammen,
die
HEISENBERG
aus
der
Unbestimmtheitsrelation abgeleitet hat.
44
5. Die Vollständigkeit der Quantenmechanik. Diese lässt keinen Raum für
zusätzliche (verborgene) Parameter.
Am JÖNSSON – Experiment (Abschnitt 3.2.2) lässt sich eine typische Aussage der
Kopenhagener Interpretation verdeutlichen: Mittels Lichtstreuung wird versucht
herauszufinden, durch welchen Spalt das Elektron gegangen ist. In diesem Fall
verschwindet das Interferenzmuster (Abschnitt 3.2.3) auf dem Schirm. Alle
Manipulationen an der Versuchsanordnung, die es ermöglichen eine Bestimmung
des Ortes zu erzielen, verändern den Ausgang des Experiments. BOHR deutet
diesen Sachverhalt so,
„[…] dass kein Ergebnis eines Experimentes über ein im Prinzip außerhalb des
Bereiches der klassischen Physik liegenden Phänomen dahin gedeutet werden kann,
dass es Aufschluss über unabhängige Eigenschaften der Objekte gibt; es ist vielmehr
unlöslich mit einer bestimmten Situation verbunden, in deren Beschreibung auch die
mit den Objekten in Wechselwirkung stehenden Messgeräte als wesentliches Glied
eingehen.“ [Boh85,
S.23].
Betrachtet man das Doppelspalt – Experiment, so bedeutet dies: Unabhängig von
einer Messung, hat ein Elektron keinen Ort [Mül99]. Die Aufgabe des
Determinismus war für manche Physiker unvorstellbar, so auch für ALBERT
EINSTEIN. Dies spiegelt sich in seinem berühmten Ausspruch „Der Alte würfelt nicht“
[Müll99] wider. Physiker wie ALBERT EINSTEIN suchten einen Ausweg und
entwickelten neue Theorien, die an die klassischen Vorstellungen der Physik
angelehnt waren. Solch eine Theorie wird im nächsten Abschnitt vorgestellt.
3.5.2 Die BOHMsche Interpretation der
Quantenmechanik
Theorien, die versuchen den Determinismus wieder in die Quantenmechanik
einzuführen, sind Theorien mit verborgenen Parametern. Es handelt sich um
Modifikationen der Quantenmechanik, bei denen der Zustand eines Quantenobjekts
noch nicht vollständig durch die Wellenfunktion bestimmt ist (Abschnitt 3.5.1). Es
45
gibt bei diesen Theorien zusätzliche Variablen, die wir nicht kennen. Beim
Doppelspalt – Experiment wäre z.B. schon im Voraus festgelegt, durch welchen
Spalt ein Elektron gehen wird. DAVID BOHM gehört zu den Physikern, die solche
Theorien entwickelten und somit ein radikal anderes Programm verfolgten, als die
Anhänger der Kopenhagener Deutung der Quantenmechanik. Die Theorie von
BOHM [Bom52] ist vollkommen deterministisch, d.h. Quantenobjekte, wie z.B.
Elektronen verhalten sich wie klassische Teilchen. BOHM beginnt in seiner Arbeit
[Bom52] zunächst mit der Herleitung einer NEWTONschen Bewegungsgleichung für
das Teilchen. Zu jedem Zeitpunkt besitzen die Elektronen einen festen Ort, womit
der Bahnbegriff der NEWTONschen Mechanik beibehalten werden kann [Müll99]. Es
stellt sich natürlich die Frage: Wie ist das möglich? Die Schrödingergleichung (2.20)
behält ihre Funktion als dynamische Gleichung für die Wellenfunktion
des
betreffenden Systems bei. Aber der Wellenfunktion (2.21) wird noch eine
zusätzliche Funktion zugewiesen, so dass sie als ‚Führungsfeld’ für ein Teilchen
wirkt. Zunächst wird die Wellenfunktion in Betrag und Phase separiert:
(x ) = R (x )e
iS ( x )
h
,
(3.17)
wobei R (x ) und S(x ) reell sind. (3.17) wird in die Schrödingergleichung (2.20)
eingesetzt. Im Folgenden betrachtet man Real- und Imaginärteil separat, so dass
man zwei Gleichungen für die beiden Größen R (x ) und S(x ) erhält. Eine Gleichung
lässt sich als Kontinuitätsgleichung für die Wahrscheinlichkeitsdichte
(x ) 2 = R (x )2
(3.18)
deuten, die andere Gleichung für die Größe S(x ) kann als HAMILTON – JACOBI –
Gleichung aufgefasst werden. Analog zur klassischen Mechanik wird das
Geschwindigkeitsfeld der Teilchen durch die Größe S(x ) bestimmt:
r S(x )
r
.
v (x ) = (
m
(3.19)
46
In der Quantenmechanik tritt im Gegensatz zur klassischen Mechanik noch ein
zusätzlicher Potentialterm auf, der als ‚Quantenpotential’ bezeichnet wird:
U (x ) = !
h 2 ( 2 R (x )
.
2 m R (x )
(3.20)
Die Bewegung der Teilchen wird durch das Quantenpotential zusätzlich zum
gewöhnlichen ‚klassischen’ Potential V beeinflusst. Betrachtet man wieder das
Doppelspalt – Experiment, so kann obige Theorie verdeutlicht werden.
Abb. 22: Bahnen der Elektronen im Doppelspaltversuch
47
Das Interferenzmuster in BOHMs Theorie kommt durch die Häufung der
Teilchenbahnen (Abbildung 22) am Ort der Maxima zustande. Sind die
Anfangsbedingungen, Ort und Impuls, der Teilchen vorgegeben, so ergibt sich eine
wohlbestimmte Teilchenbahn. Da die verborgenen Parameter in der BOHMschen
Theorie genau die Orte der Teilchen sind, und somit in einem Experiment nicht
gezielt präparierbar und kontrollierbar sind, muss über sie gemittelt werden, so dass
die Reproduktion der statistischen Aussagen der Quantenmechanik gelingt. BOHM
konnte zeigen, dass die Wahrscheinlichkeitsverteilung
( x, t ) 2
für die Teilchenorte
durch die oben erwähnte Mittelungsprozedur zustande kommt, sofern die
Wahrscheinlichkeitsverteilung zu einem Anfangszeitpunkt
(0, t ) 2
gegeben war
[Mül99].
48
4. Der Quantenradierer
Am Doppelspalt – Experiment lassen sich die vorrangigen Charakteristika
(Abschnitt
5.4)
der
Quantenphysik
aufzeigen.
Allerdings
lässt
sich
das
Komplementaritätsprinzip (Abschnitt 3.2.3) am Doppelspalt nur in Form einer
Simulation erarbeiten (Abschnitt 5.6.2.1). Das MACH – ZEHNDER – Interferometer
bietet die Möglichkeit die Komplementarität auch als Realexperiment zu zeigen. Als
Zusatz kann sogar die ‚Welcher – Weg’ – Information nachträglich wieder
ausgelöscht werden, wodurch solch eine experimentelle Anordnung auch
Quantenradierer genannt wird. In diesem Kapitel werden die theoretischen
Grundlagen und die Realisierung des Quantenradierers als Realexperiment
behandelt.
4.1 Interferenz an einem realen
MACH – ZEHNDER – Interferometer
In Abschnitt 3.3 wurde ein idealisiertes MACH – ZEHNDER - Interferometer (Abbildung
23) betrachtet.
Abb. 23: Das MACH – ZEHNDER – Interferometer
49
In diesem Fall wurde die Ausrichtung der Teilstrahlen als ideal koaxial betrachtet,
was bedeutet, dass die Phasenfronten (Abbildung 24 a) der Teilstrahlen genau
parallel verlaufen. Die in Abschnitt 3.3 beschriebene Idealjustage ist in der Praxis
nicht immer zu erreichen.
Abb. 24: Entstehung von Interferenzstreifen
Aus diesem Grund erhält man nicht mehr eine einheitliche Intensität auf beiden
Detektorflächen bzw. Schirmen. Zwischen den Phasenfronten besteht ein
Neigungswinkel wie in Abbildung 24 b und c dargestellt ist.
Abb. 25: Entstehung von Interferenzringen
50
Die Überlagerung der Wellentäler bzw. -berge, die durch Geraden dargestellt sind,
findet nur noch an diskreten Linien statt, wodurch sich ein streifenförmiges
Interferenzmuster (Abbildung 24 d) ergibt. Der Abstand der Streifen ist abhängig
vom Verkippungswinkel. Mit zunehmendem Verkippungswinkel verkleinern sich die
Abstände der Streifen. Parallel verlaufende Phasenfronten entsprechen dem
Grenzfall unendlich entfernter Streifen [Moh00].
Speziell bei Verwendung von Laserlicht liegt eine longitudinale und radiale
Abhängigkeit des Feldes vor. Dies äußert sich darin, dass die Phasenfronten keine
ebene Charakteristik mehr aufweisen, wie im oben behandelten Fall. Die
Phasenfronten sind nun Ausschnitte von Kugelflächen, sogenannte sphärische
Wellen. In Abbildung 25 a sind die sphärischen Phasenfronten schematisch
angedeutet. Die Entstehung der sphärischen Phasenfronten erfolgt durch die
Lichtausbreitung aus einem mit einer Linse erzeugten Brennpunkt. Kommt eine
sphärische Wellenfront mit einer ebenen Wellenfront (Abbildung 25 b) zur
Überlagerung, so ergibt sich ein Interferenzsystem gleicher geometrischer
Charakteristik. Es entsteht ein Kreissystem, sogenannte Interferenzringe, wie in
Abbildung 25 c dargestellt ist. Im Allgemeinen liegt nicht der Fall einer ebenen und
sphärischen Wellenfront vor, sondern es handelt sich um zwei sphärische Wellen.
Aber auch in diesem Fall muss ein Interferenzringsystem entstehen, wenn die
Krümmungsradien beider Wellenfronten verschieden sind. Weil die überlagerten
Wellen im MACH – ZEHNDER – Interferometer eine unterschiedliche Geometrie
durchlaufen, ist dies zunächst auch der Standardfall [Moh00].
Dies erklärt, warum in vielen Lehrbüchern das Interferenzmuster als Ringsystem
dargestellt wird [Dem99]. Aus Intensitätsgründen ist am anderen Detektor bzw.
Schirm, das komplementäre Muster zu erkennen, d.h., ist bei Detektor 1 ein dunkler
Ring, so ist bei Detektor 2 ein heller Ring [Moh00]. Da jetzt die auftretenden Fälle
bei einem realen MACH – ZEHNDER – Interferometer diskutiert wurden, kann auf das
eigentliche
Prinzip
des
Quantenradierers
eingegangen
werden.
Da
beim
Quantenradierer Polarisationsfilter eingesetzt werden, wird zunächst noch die
Wirkung von Polarisationsfiltern auf Photonen betrachtet.
51
4.2 Polarisation von Photonen
Ein Lichtstrahl der Intensität I 0 trifft auf einen Polarisationsfilter, welcher um den
Winkel
zur ursprünglichen Polarisationsrichtung des Lichtstrahls verkippt ist. In
diesem Fall beträgt die Intensität des Lichtstrahls nach dem Polarisationsfilter nur
noch
I = I0
cos 2 (
).
(4.1)
Dies konnte aus der Annahme, dass Licht eine elektromagnetische Welle ist,
hergeleitet werden (Abschnitt 2.1). Es wurde aber auch gezeigt, dass Licht aus
Photonen besteht (Abschnitt 2.3). Den Photonen kann in der gleichen Weise eine
Polarisationsrichtung zugeordnet werden, analog zur Polarisationsrichtung einer
elektromagnetischen Welle. Betrachtet man einen Laser, so sind die erzeugten
Photonen nicht nur monochromatisch, sondern sie haben auch alle dieselbe
Polarisationsrichtung.
Bei einer klassischen Welle konnte die Gleichung (4.1) durch die Zerlegung des
elektrischen Feldvektors in eine durchgelassene und absorbierte Komponente
hergeleitet werden. Allerdings ist das Photon unteilbar und wird somit entweder als
‚Ganzes’ durchgelassen oder absorbiert. Das Photon richtet jedoch seine
Polarisationsrichtung parallel zur Durchlassrichtung des Polarisationsfilters aus,
falls es durchgelassen wird.
Es stellt sich nun die Frage, wie die Abschwächung des Lichts mit der
Photonenhypothese vereinbar ist. Da die klassische Intensität I des Lichts
proportional zur Anzahl der Photonen ist, gibt das Verhältnis der Intensitäten des
Lichtstrahls vor und nach dem Durchgang durch den Polarisationsfilter die
Wahrscheinlichkeit an, dass ein Photon den Filter durchdringen kann. Die
Transmissionswahrscheinlichkeit ist somit durch
P(
)trans
=
I
= cos 2 (
I0
)
(4.2)
52
gegeben. Für die Absorptionswahrscheinlichkeit folgt nach der Zerlegung des
elektrischen Feldes in die absorbierende Komponente (Abschnitt 2.1):
P(
)abs
= sin 2 ( ) .
(4.3)
Somit ergibt sich für die Summe von (4.2) und (4.3) [Gug06]:
Pabs + Ptrans = sin 2 (
) + cos 2 ( ) = 1 .
(4.4)
4.3 Die Funktionsweise des Quantenradierers
Um einen Quantenradierer zu realisieren wird das MACH – ZEHNDER –
Interferometer mit drei verstellbaren Polarisationsfiltern ausgestattet. Die Positionen
der Polarisationsfilter sind in Abbildung 26 dargestellt.
Polarisationsfilter 2
Polarisationsfilter 3
Polarisationsfilter 1
Abb.26: MACH – ZEHNDER – Interferometer als Quantenradierer
Werden ohne Polarisationsfilter einzelne Photonen in das MACH – ZEHNDER –
Interferometer
geschickt,
so
entsteht
nach
einer
gewissen
Zeit
ein
Interferenzmuster (Abschnitt 3.2.1). Der Unterschied zum TAYLOR – Experiment
liegt jedoch in der Form des Interferenzmusters. Im Falle des MACH – ZEHNDER –
53
Interferometers entsteht ein Ringsystem (Abschnitt 4.1), wobei der allmähliche
Aufbau des Interferenzmusters in Abbildung 27 zu erkennen ist.
Abb.27: Aufbau des Interferenzmusters aus den Spuren einzelner Photonen
Die Polarisationsfilter werden ausgenutzt, um eine ‚Welcher – Weg’ – Markierung
vorzunehmen. Werden zunächst nur Polarisationsfilter 1 und 2 eingebaut und
parallel ausgerichtet, so sieht man auf dem Schirm ein Interferenzmuster
(Abbildung 27). Da die beiden Polarisationsfilter parallel ausgerichtet sind, ist keine
Aussage über den Weg, den ein Photon gelaufen ist, möglich, denn beide
Photonen besitzen die gleiche Polarisation. Würde man die Polarisation hinter dem
zweiten Strahlteiler messen, so kann man keine Aussage über den Weg treffen,
den ein Photon zurückgelegt hat.
Werden die Polarisationsfilter 1 und 2 so verdreht, dass sie einen Winkel von 90°
bilden, so liegt eine ‚Welcher – Weg’ – Information vor. Dazu kann man z.B.
Polarisationsfilter 1 in 45° Stellung und Polarisationsfilter 2 in -45° Stellung bringen
In dieser Stellung erscheint kein Interferenzmuster mehr, da eine ‚Welcher – Weg’ –
Information über die Photonen vorliegt. Die Polarisationsrichtung der Photonen wird
folgendermaßen ausgenutzt: Polarisationsfilter 3 (Abbildung 26) kann als
Analysator benutzt werden. Ist die Stellung von Polarisationsfilter 3 genauso wie die
Stellung von Polarisationsfilter 2, können nur die Photonen durchkommen, die den
Weg genommen haben, in dem sich Polarisationsfilter 2 befindet. Trifft ein Photon
auf den Schirm, so weiß man mit Sicherheit welchen Weg es genommen hat.
Analog kann man den Polarisationsfilter 3 in die gleiche Stellung wie
Polarisationsfilter 1 bringen und erhält eine Information über den anderen Weg. In
54
diesem Fall ist der Weg des Photons eindeutig durch die Polarisationsrichtung
bestimmt, so dass kein Interferenzmuster entstehen kann.
Das Verblüffende ist allerdings, dass man den Polarisationsfilter 3 nicht einbauen
muss, damit das Interferenzmuster verschwindet. Es reicht schon, dass die
Photonen die ‚Welcher – Weg’ – Information tragen, obwohl diese Information nicht
beobachtet wird.
Mit Hilfe des dritten Polarisationsfilters kann die ‚Welcher – Weg’ – Information
wieder gelöscht bzw. ausradiert werden. Dazu wird Polarisationsfilter 3 so in den
Strahlengang
gebracht,
dass
der
Filter
in
Mittelstellung
(0°)
ist.
Das
Interferenzmuster erscheint wieder, allerdings mit einer abgeschwächten Intensität,
da die Polarisationsfilter einen Teil der Intensität absorbieren. Um das Erscheinen
des Interferenzmusters zu erklären, werden die Transmissionswahrscheinlichkeiten
(Abschnitt 4.2) der Photonen aus beiden Wegen am Analysator betrachtet. Weg A
sei der Weg, in dem Polarisationsfilter 1 steht, und Weg B sei der Weg, in dem
Polarisationsfilter
2
steht.
Für
die
Transmissionswahrscheinlichkeiten
am
Analysator ergibt sich:
2
' 1$
1
" =
PA = Ptrans (45°) = cos (45°) = %%
"
2
& 2#
2
(4.5)
2
' 1$
1
" = .
PB = Ptrans (! 45°) = cos (! 45°) = %%
"
2
& 2#
2
(4.6)
Die Transmissionswahrscheinlichkeiten der Photonen von beiden Wegen sind
identisch, so dass nur mit einer 50% Chance der richtige Weg erraten werden kann.
Dies kann durch die sogenannte Vorhersagbarkeit P = PA ! PB
ausgedrückt
werden. In diesem Fall erhält man P = 0 , was gleichbedeutend ist mit der
vollkommenen Unbestimmtheit des Weges. Aus diesem Grund zeigt sich wieder
das gewohnte Interferenzmuster. Bilden Polarisationsfilter 1 und 2 (ohne
Polarisationsfilter
3)
keinen
exakten
90°
Winkel,
sondern
irgendeine
Zwischenstellung von 0° bis 90°, so kann nicht mehr mit Sicherheit der Weg eines
Photons bestimmt werden, so dass das Interferenzmuster teilweise erkennbar wird.
Je mehr ‚Welcher – Weg’ – Information vorliegt, desto verschwommener ist das
55
Interferenzmuster [Gug06]. Die obige Betrachtungsweise bezieht sich auf einzelne
Photonen. Wird der Versuch mit Licht hoher Intensität (Laserlicht) durchgeführt, so
können die Versuchsergebnisse auch klassisch erklärt werden. Wenn die
Polarisationsfilter 1 und 2 in gekreuzte Stellung (90° Winkel) verdreht werden, so
stehen die elektrischen Felder senkrecht aufeinander und interferieren nicht. Durch
den dritten Polarisationsfilter, in Mittelstellung (0° Winkel), werden aus den beiden
senkrecht stehenden elektrischen Feldvektoren wieder die Anteile parallel zur
Mittelstellung herausprojiziert. Durch diese Projektion auf die Mittelstellung des
dritten Polarisationsfilters sind beide Teilstrahlen wieder parallel und können
interferieren.
4.4 Der Aufbau des Quantenradierers als
Realexperiment
Da die Funktionsweise und das Interferenzmuster eines Quantenradierers
ausführlich dargestellt wurden kann in diesem Abschnitt auf den im Rahmen dieser
Staatsexamensarbeit entwickelten Aufbau eines Quantenradierers mit Laserlicht
hoher Intensität eingegangen werden.
Der Quantenradierer lässt sich auch mit optischen Bausätzen von Lehrmittelfirmen
realisieren (z.B. LEYBOLD DIDACTIC GmbH [Ley07] und PHYWE SYSTEME
GmbH & Co. Kg [Phy07]), wobei die Bausätze jedoch einen entscheidenden
Nachteil besitzen. Der Hauptnachteil liegt im hohen Justageaufwand. Ein weiterer
Nachteil ist der hohe Preis von ca. 4500€ für die Bausätze der Lehrmittelfirmen
[Ley07]
und
[Phy07].
Der
Preis
des
Quantenradierers,
der
in
dieser
Staatsexamensarbeit aufgebaut wird, beträgt lediglich ca. 2650€. In Anhang B sind
die einzelnen Bauteile mit Preis aufgelistet. Die Ziele des im Rahmen dieser
Staatsexamensarbeit realisierten Quantenradierers sind die Minimierung des
Justageaufwands, eine gute Transportfähigkeit und ein einfach zu durchschauender
Versuchsaufbau. Eine gute Transportfähigkeit soll gewährleistet werden um
einerseits
den
Versuchsaufbau
problemlos
an
Schulen
auszuleihen
und
andererseits den Versuchsaufbau als Lehrmittel an der Universität einzusetzen,
ohne einen großen Zeitaufwand in den Aufbau des Quantenradierers investieren zu
56
müssen.
Allerdings
ist
der
in
dieser
Staatsexamensarbeit
verwirklichte
Quantenradierer vorwiegend als Demonstrationsexperiment geeignet und die
einzelnen Komponenten des Versuchsaufbaus können nicht anderweitig eingesetzt
werden. Hier bieten die Bausätze der Lehrmittelfirmen jedoch mehr Flexibilität, so
dass die einzelnen Bauteile auch anderweitig eingesetzt werden können. Der
Versuchsaufbau dieser Arbeit kann allerdings ebenfalls als MACH – ZEHNDER –
Interferometer
für
andere
Versuchszwecke
(z.B.
die
Bestimmung
von
Brechungsindizes) ausgerüstet werden, so dass die Flexibilität nicht ganz
eingeschräkt ist. Anregungen und Ideen für die Verwirklichung des Projektes gab
eine Experimentieranleitung [Moh00] zum Zweistrahl – Interferometer der Firma
LINOS PHOTONICS GmbH & Co [Li07] in Göttingen. Bei LINOS PHOTONICS
wurden die Bauteile für den Versuchsaufbau bestellt. Der Versuchsaufbau ist in
Abbildung 28 dargestellt.
Blende
Spiegel
Polarisationsfilter
Strahlteiler
Strahlteiler
Linse
Laserdiode
Spiegel
Polarisationsfilter
Blende
Polarisationsfilter
Abb. 28: Der Quantenradierer als Realexperiment
Die Maße der Bauteile des Mikrobanksystems sind präzise aufeinander
abgestimmt. Die Montageplatte wurde von der universitätsinternen mechanischen
Werkstatt hergestellt und besitzt folgende Maße (Abbildung 29): A: 600mm;
B: 250mm; C: 20mm; D: 10mm; E: 10mm.
57
Abb. 29: Montageplatte
Die Bohrungen in Abbildung 29 besitzen kein Gewinde. Die Montageplatte ist mit
ihren Maßen angelehnt an die Montageplatten der Firma LINOS PHOTONICS. Die
Maße A und B wurden jedoch dem hier vorliegenden Versuchaufbau so angepasst,
dass der Quantenradierer auf der Montageplatte aufgebaut werden konnte, aber
immer noch eine gute Transportfähigkeit gewährleistet ist. Zusätzlich wurden noch
weitere Bohrungen (M6 Gewinde) angefertigt die in Abbildung 29 nicht enthalten
sind.
Aufnahmeplatte
Halterungen
Abb.30: Stangensystem
58
Die zusätzlichen Bohrungen wurden für optionale Anbauten eingefügt, wobei die
Bohrungen bei dem vorliegenden Versuchsaufbau (Abbildung 28) nicht verwendet
wurden. Als Halterungen für die einzelnen Bauteile diente ein Stangensystem
(Abbildung 30). Die Stangen haben einen Durchmesser von 6mm und sind in
verschiedenen Längen von 20 bis 450mm bei LINOS PHOTONICS erhältlich. Bei
diesem Versuchsaufbau wurden nur Stangen der Länge 150mm eingesetzt. Die
Stangen wurden über Halterungen (Abbildung 30) mit Gewinde (M4) auf der
Montageplatte
befestigt.
Für
weitere
Bauteile
(z.B.
Linsen,
Irisblenden,
Laserdioden, …) dienten sogenannte Aufnahmeplatten (Abbildung 30) als
Halterungen. Die Aufnahmeplatten sind in verschiedenen Durchmessern erhältlich,
wobei für diesen Versuch alle Aufnahmeplatten einen Durchmesser von 25mm,
außer den Aufnahmeplatten der Polarisationsfilter, besitzen. Als Halterungen für die
Strahlteiler und die Spiegel wurden sogenannte Umlenkwürfel (Abbildung 31)
benutzt. Die Umlenkwürfel besitzen einen drehbaren Plattenhalter in Zylinderform.
Abb. 31: Umlenkwürfel
In die Umlenkwürfel können Strahlteilerplatten und Spiegel mit den Maßen
20 × 30mm eingebaut werden, welche durch Aufkleben auf die drehbaren
Plattenhalter befestigt werden. Als Drehhilfe wurde zusätzlich ein Stellring
angebracht (Abbildung 31). Die eingesetzten Spiegel (20 × 30mm) besitzen eine
Aluminiumbeschichtung
(RAL)
und
eine
Dicke
von
2,5mm.
Das
Reflexionsvermögen der Spiegel für verschiedene Wellenlängen ist in Abbildung 32
dargestellt.
59
Abb. 32: Reflexionsvermögen in Abhängigkeit der Wellenlänge
Die Strahlteiler T50 (20 × 30mm) sind 2,5 mm dick und reflektieren bzw.
transmittieren annähernd 50% der Lichtintensität (Abbildung 33).
Abb. 33: Transmissionsvermögen in Abhängigkeit der Wellenlänge
Die Spiegel und Strahlteiler können somit als nahezu ideale Spiegel bzw.
Strahlteiler angesehen werden. Abbildung 32 und 33 sind Herstellerangaben.
Als Lichtquelle wurde eine 0,9mW Laserdiode (Laserschutzklasse II) mit 635nm
Wellenlänge verwendet (Abbildung 34).
60
Abb. 34: Laserdiode
Die Laserdiode besitzt ein elliptisches Strahlprofil, das sehr divergent ist. Dadurch
wurde keine Aufweitungslinse benötigt und weitere Intensitätsverluste wurden
vermieden. Der Durchmesser der Laserdiode ist allerdings an das Nanobanksystem
von LINOS PHOTONICS angepasst, so dass ein Reduzierring (25/16mm) zum
Einbau in das Mikrobanksystem benötigt wurde. Das Mikrobanksystem gab eine
optische Achshöhe von 40mm vor, wodurch der Laserstrahl im gesamten Aufbau
parallel zur Montageplatte verläuft. Um die Parallelität des Laserstrahls beim Eintritt
in die Versuchsanordnung zu gewährleisten, wurde zusätzlich die Laserdiode in
eine Zentrieraufnahmeplatte (Abbildung 35) eingesetzt, welche einen Stellweg von
± 1mm besitzt.
Abb. 35: Zentrieraufnahmeplatte
Wird der Aufbau nun ordnungsgemäß justiert (Abschnitt 4.5), so erhält man ein
Interferenzstreifensystem
(Abschnitt
4.1).
Da
viele
Lehrbücher
das
Interferenzmuster jedoch als Ringsystem darstellen, wurde eine zusätzliche
Bikonvexlinse (f = 80mm) in einen Strahlweg (Abschnitt 4.1) eingebaut (Abbildung
61
28) um die Schüler nicht mit unnötigen Problemen bezüglich der Entstehung des
Interferenzmusters, zu konfrontieren. Die Polarisationsfilter wurden drehbar in
einklinkbare Aufnahmeplatten (Abbildung 36) mit einem Durchmesser von 30mm
eingesetzt. Die Aufnahmeplatten können somit aus dem Versuchsaufbau geklappt
werden.
Abb. 36: Einklinkbare Aufnahmeplatte
Zwischen Laserdiode und Strahlteiler HS1 (Abbildung 37) wurden zusätzliche
Aufnahmeplatten eingebaut, die zum einen optionale Bauteile aufnehmen können
und zum anderen zur Justage des Laserstrahls dienen. Eine zusätzliche
Aufnahmeplatte wurde auch auf der gegenüberliegenden Seite nach Strahlteiler
HS2 angebracht. Die Blenden wurden eingesetzt um nur die relevanten
Interferenzringe darzustellen, da die Linse den einen Teilstrahl stark aufweitete. Die
Blendenhalterungen wurden auch von der universitätsinternen mechanischen
Werkstatt angefertigt, wobei die Aufnahmeplatten und die Irisblenden von LINOS
PHOTONICS stammten.
4.5 Die Justage des Quantenradierers
Der Laser ist normalerweise so eingebaut, dass er parallel zur Grundplatte verläuft.
Sollte dies jedoch nicht so sein, können die Aufnahmeplatten (Abbildung 37) mit
den Irisblenden bestückt werden, die sich in den Blendenhalterungen am Ausgang
des Quantenradierers befinden. Zusätzlich kann eine dritte Aufnahmeplatte
(Abbildung 38) zwischen Strahlteiler HS1 und Spiegel S1 (Abbildung 37) gebracht
werden, um die Parallelität über eine größere Strecke zu überprüfen. Die
Irisblenden werden so weit zugefahren, dass nur noch ein kleines Loch sichtbar ist.
62
Strahlteiler HS1
Laserdiode
Spiegel S1
Linse
Blende
Polarisationsfilter 2
Strahlteiler HS2
Aufnahmeplatten
Spiegel S2
Polarisationsfilter 3
Polarisationsfilter 1
Blende
Abb. 37: Aufbau des Quantenradierers
Abb. 38: Aufnahmeplatte
Der Laserstrahl muss ungehindert durch beide Öffnungen (Irisblende 1 und
Irisblende 2) treten, ohne an der Verkleidung der Irisblende reflektiert zu werden. In
diesem Fall verläuft der Laserstrahl parallel zur Montageplatte, da die Irisblenden
dieselbe optische Achshöhe besitzen (Abschnitt 4.4). Die Ausrichtung des
Laserstrahls ist über zwei Schrauben an der Aufnahmeplatte der Laserdiode
möglich (die Schrauben sind sehr schwergängig). Sei der Laserstrahl nun parallel
zur Grundplatte, werden die Blendenhalterungen zunächst entfernt, indem man
zuerst die schwarzen Deckel abmontiert und danach die Aufnahmeplatten entfernt.
Die Polarisationsfilter (1 bis 3) werden zunächst aus dem Versuchsaufbau
herausgeklappt und die Irisblenden, die zur Ausrichtung des Laserstrahls nötig
waren, werden entfernt. Zunächst wird der Strahlteiler HS1 mit dem Stellring in 45°
Stellung zum einfallenden Laserstrahl gebracht, so dass der Strahlverlauf
63
entsprechend Abbildung 37 ist. Die Spiegel S1 und S2 werden nun so gedreht,
dass der Laserstrahl in den Strahlteiler HS2 gelangt. Strahlteiler HS2 wird ebenfalls
in 45° Stellung gebracht, so dass die Teilstrahlen an beiden Ausgängen
überlappen. Für eine bessere Sichtbarkeit des Interferenzmusters wird empfohlen,
den Schirm in ca. 2 bis 3m Abstand aufzustellen und den Raum etwas
abzudunkeln. Um nun die gewünschte Ringstruktur zu erhalten, wird zunächst nur
der Ausgang betrachtet, in dem Polarisationsfilter 3 angebracht ist. Man sieht einen
kleinen intensiven Lichtfleck und einen großen schwächeren Lichtfleck, der von der
Linse kommt. Das Interferenzmuster wird dann sichtbar, wenn der intensivere
Lichtflecke etwas aus der Mitte des schwächeren Lichtflecks, nach rechts
ausgelenkt wird (Abbildung 39). Es kann sein, dass man nicht direkt eine
Ringstruktur erhält. In diesem Fall muss mit dem intensiveren Lichtfleck langsam
über
den
anderen
schwächeren
Lichtfleck
gefahren
werden,
bis
das
Interferenzmuster zu erkennen ist.
Abb. 39: Ringförmiges Interferenzmuster
Es treten allerdings auch weitere Ringstrukturen auf, die z.B. durch verschmutzte
optische Bauteile verursacht werden. Um zu testen, ob es sich um das gewünschte
Ringsystem handelt, kann man mit kurzen zarten Schlägen auf die Montageplatte
klopfen. Verändert sich das Ringsystem bei Erschütterung der Montageplatte, so
handelt es sich um das gewünschte Interferenzmuster und die Justage ist beendet.
Falls kein Interferenzmuster zu beobachten ist, kann die Linse etwas vor oder
zurück
geschoben
und
ein
neuer
Justierversuch
gestartet
werden.
Die
Verschiebung der Linse ist allerdings in den seltensten Fällen notwendig. Nun
können die Irisblenden wieder in die Blendenhalterungen eingebaut werden und so
justiert werden, dass fast ausschließlich die Ringstruktur zu erkennen ist.
64
4.6 Komplementarität am realen Quantenradierer
Um die Komplementarität (Abschnitt 4.3) zu zeigen, müssen die Polarisationsfilter
entsprechend
eingestellt
werden.
Die
Polarisationsfilter
besitzen
eine
Winkelskalierung, die in 5° Skalenteile unterteilt ist. Zunächst werden alle
Polarisationsfilter aus der Versuchsanordnung (Abbildung 37) entfernt. Man
beobachtet ein Interferenzringsystem (Abschnitt 4.3), das in Abbildung 40
dargestellt ist.
Abb. 40: Interferenzmuster bei keiner ‚Welcher – Weg’ – Information
Die Interferenzringe in Abbildung 40 werden beobachtet, da man keine ‚Welcher –
Weg’ – Information über die Photonen besitzt (Abschnitt 4.3). Werden die
Polarisationsfilter 1 und 2 in die Versuchsanordnung (Abbildung 37) geklappt und in
gekreuzte Stellung (90° Winkel) gebracht, so besitzen die Photonen eine ‚Welcher –
Weg’ – Information und das Interferenzmuster verschwindet (Abbildung 41).
Abb. 41: Kein Interferenzmuster bei ‚Welcher – Weg’ – Information
Wird Polarisationsfilter 3 in Mittelstellung (0° Winkel) zu den gekreuzten
Polarisationsfiltern 1 und 2 eingestellt, so wird die ‚Welcher – Weg’ – Information
wieder ausgelöscht und das Interferenzmuster erscheint wieder (Abbildung 42).
65
Abb. 42: Interferenzmuster bei Auslöschung der ‚Welcher – Weg’ – Information
In Abbildung 41 ist noch ein schwaches Ringsystem zu erkennen, da die
Polarisationsfilter nicht exakt eingestellt werden können. Aber im Vergleich zu den
anderen beiden Interferenzmustern (Abbildung 40 und 42) ist in Abbildung 41 zu
erkennen,
dass
das
Interferenzmuster
nicht
mehr
vorhanden
ist.
Die
Intensitätsverluste in Abbildung 41 und 42 werden durch die Polarisationsfilter
verursacht, welche einen Teil der Laserintensität absorbieren.
66
5. Planung und Durchführung des
Schülerlabors
5.1 Vorbemerkung
Forschungsprozesse sind in Naturwissenschaften und Technik geprägt durch
Neugier,
Originalität
und
ein
hohes
Maß
an
Kreativität,
während
die
entsprechenden Schulfächer ein eher gegenteiliges Bild vermitteln. Die Physik gilt
nicht nur als schwieriges Schulfach, sondern auch als wenig attraktiv und
langweilig. Das Fach Physik „lädt kaum zur Beteiligung und zur kreativen Entfaltung
ein“ [Eul05, S.4]. Das Schülerinteresse lässt zwar generell im Verlauf der
Sekundarstufe 1 nach, doch vor allem sind besonders die Naturwissenschaften
Physik
und
Chemie
betroffen
[Eul05].
Somit
ergibt
sich
auch
eine
besorgniserregende Bereitschaft, solch ein Fach zu studieren bzw. einen mit
Naturwissenschaften zusammenhängenden Beruf zu ergreifen. Angesichts dieses
Zustands
und
nicht
zuletzt
wegen
der
Sorge
um
qualifizierten
naturwissenschaftlichen Nachwuchs werden Schülerlabore entwickelt.
Schülerlabore
sind
heute
ein
wichtiger
Bestandteil
der
außerschulischen
Bildungsmöglichkeit in der Physik, da Schüler sich in dieser Lernumgebung vor
allem
ohne
Leistungsdruck
den
physikalischen
Inhalten
widmen
können.
Schülerlabore sollten zum einen das „Interesse und die Aufgeschlossenheit“ von
Schülern gegenüber „Naturwissenschaft und Technik“ fördern, zum anderen aber
auch ein „zeitgemäßes Bild von Naturwissenschaften […] und ihrer Bedeutung für
unsere Gesellschaft“ vermitteln. Nicht zuletzt sollte auch die Möglichkeit „des
Dialoges und der Auseinandersetzung mit aktuellen, z.T. kontrovers diskutierten
Themen naturwissenschaftlicher Forschung geschaffen werden“ [Eul05, S.1]. Die
Quantenmechanik bietet zum Erfüllen dieser Zielsetzungen genügend Potential.
Aus diesem Grund wurde im Rahmen dieser Staatsexamensarbeit ein zweitägiges
Schülerlabor
zur
Quantenmechanik
entwickelt.
Vor
allem
bietet
die
Quantenmechanik Einblick in eine wissenschaftliche Debatte: Die Interpretationen
der Quantenmechanik, die noch nicht abgeschlossen ist und noch immer
67
kontrovers diskutiert wird. Die Quantenmechanik bietet den Schülern auch Wissen
über das Weltbild der modernen Physik (Ende des Determinismus), die unter
physikalischer Perspektive unsere Vorstellung von der Beschaffenheit der Natur
maßgeblich geprägt hat. Somit bietet dieses Schülerlabor den Schülern die
Gelegenheit, über das naturwissenschaftliche Weltbild des 19. Jahrhunderts
hinauszukommen [Wie00]. Dadurch sollen die Schüler auch erkennen, dass es
noch offene Fragen (Abschnitt 3.5) in der Physik gibt, welche im Schülerlabor
diskutiert werden können, da solche Fragen, wie die Interpretationen der
Quantenmechanik, selten im normalen Unterricht thematisiert werden. Natürlich
stellt sich auch die Frage nach Synergien von einem Schülerlabor und
traditionellem Physikunterricht. Aus diesem Grunde wurden die fachlichen Inhalte
des Schülerlabors so konzipiert, dass sie im direkten Bezug zum Lehrplan Physik
(MSS/Leistungsfach) in Rheinland – Pfalz stehen, wodurch eine Einbindung in den
Unterricht ermöglicht wird.
5.2 Bezug zum Lehrplan
Die Struktur des Lehrplans (Jahrgangsstufe 11 – 13) in Rheinland – Pfalz ist an ein
Baukastensystem angelehnt, es gibt Pflichtbausteine (grau unterlegt) und
Wahlpflichtbausteine (weiß unterlegt). Pflichtbausteine müssen behandelt werden
und Wahlpflichtbausteine werden eigenverantwortlich von der Lehrkraft ausgewählt
[Lpr07].
Die
Wahlpflichtbausteine
sind
lediglich
in
der
Gesamtzahl
(13)
vorgeschrieben. Da die Adressaten des Schülerlabors Leistungskursschüler der
Jahrgangstufe 12 sind, wird im Folgenden der Lehrplan des Leistungsfaches Physik
betrachtet, und dabei werden die im Schülerlabor angesprochenen Bausteine
vorgestellt.
68
69
Die Inhalte der Bausteine werden nicht alle thematisiert. Das genaue Konzept wird
im nächsten Abschnitt erläutert.
70
5.3 Das Konzept des Schülerlabors
Alle Materialien die im Schülerlabor verwendet werden, sind auf einer CD beigefügt.
In Anhang C befindet sich eine Auflistung dieser Materialien.
Das Schülerlabor findet an zwei Tagen, zu je fünf Zeitstunden statt. Am ersten Tag
wird ein einführender Vortrag (Abschnitt 5.5.1) gehalten. Das Schülerlabor richtet
sich an Leistungskursschüler, welche die Wellenoptik behandelt haben sollten. Falls
diese Vorkenntnisse nicht vorhanden sind, ist der Einführungsvortrag so aufgebaut,
dass die für das Schülerlabor relevanten physikalischen Inhalte der Wellenoptik
vorgestellt werden. Falls die Vorkenntnisse vorhanden sind, so ist der erste Teil des
Einführungsvortrags eine Wiederholung. Anschließend wird als Lehrmethode ein
Stationenlernen (die Stationen werden zyklisch von den Schülern durchlaufen) mit
drei Stationen (Abschnitt 5.5.2) durchgeführt:
-
Station 1: Doppelspaltexperiment mit Laserlicht hoher Intensität und eine
Simulation zum Doppelspalt – Experiment mit Kugeln und Elektronen
-
Station 2: Photoeffekt
-
Station 3: Elektronenbeugung an Graphit
Als übergeordnetes Lernziel dieser Stationen sollte der Widerspruch ‚Welle’ oder
‚Teilchen’ zum Nachdenken anregen. Der zweite Tag beginnt wieder mit einem
einführenden Vortrag (Abschnitt 5.6.1), welcher den Konflikt: ‚Welle’ oder ‚Teilchen’
auflösen soll, so dass keine dualistische Denkweise entsteht und die Phänomene
der Quantenmechanik als ‚Ganzes’ gesehen werden (Abschnitt 5.4). Im weiteren
Verlauf erarbeiten sich die Schüler in drei Gruppen (Abschnitt 5.6.2) die
Komplementarität am Doppelspalt und am MACH – ZEHNDER – Interferometer, die
Interpretationen
der Quantenmechanik
(Kopenhagen
und
BOHM)
und
die
‚wechselwirkungsfreie Messung’, wobei nicht jede Gruppe diese Inhalte behandelt
(Abschnitt 5.6.2). Aus diesem Grund präsentieren die Gruppen ihre Ergebnisse den
Mitschülern, um so einen gleichen Wissensstand zu erreichen. Durch das
eigenständige Experimentieren, welches durch Arbeitsblätter (Anhang C1 und C2)
angeleitet wird, soll ein aktiver Lernprozess geschaffen werden. Die gestufte
Heranführung der Schüler an die Quantenphysik ist eine weitere didaktische
71
Zielsetzung des erläuterten Konzepts. Die Aktivität der Intelligenz beruht nach
Piaget auf einem Interesse [Pi72]. Zum einen soll die Motivation durch die
technischen Anwendungen der Quantenphysik im Einführungsvortrag (Abschnitt
5.5.1) das Interesse wecken und zum anderen soll die Konfliktschaffung von ‚Welle’
oder ‚Teilchen’ durch die Experimente am ersten Tag das Interesse verstärken und
somit die Spannung für den zweiten Tag aufrechterhalten. Dadurch erfolgt eine
gute Basis für motiviertes und eigenständiges Arbeiten am zweiten Tag, wodurch
wieder ein aktiver Lernprozess seitens der Schüler erfolgen kann. Die detaillierte
Beschreibung, Zielsetzung und didaktischen Aspekte der Versuche (vor allem des
Doppelspalt – Experiments) und Vorträge werden in den folgenden Abschnitten
vorgestellt.
5.4 Das Doppelspalt – Experiment als didaktischer
Alleskönner
FEYNMAN schätzt die Rolle und Bedeutung des Doppelspalt – Experiments
folgendermaßen ein: „Das zentrale Geheimnis der Quantentheorie steckt im
Doppelspaltexperiment“ [Le02, S. 5]. In seinen Büchern nimmt er immer wieder
Bezug auf das Doppelspalt – Experiment. Im Hinblick auf ein Schülerlabor oder den
Unterricht stellen sich folgende Fragen:
-
„Was steckt alles im Doppelspaltexperiment?
-
Ist
das
Doppelspaltexperiment
didaktisch
tragfähig
und
methodisch
elementarisierbar?“ [Le02, S.6].
In Kapitel 3 wurde aufgezeigt, welche Wesenszüge der Quantenphysik im
Doppelspalt – Experiment enthalten sind [Le02]:
-
‚Körniges’ (Quantelung)
-
‚Welliges’ (Interferenzmuster)
-
‚Stochastisches’ (Stochastische Verteilung der Einzeltreffer)
-
Der Messprozess (Komplementaritätsprinzip)
-
Interpretationen der Quantenmechanik
72
Somit ist nach JOSEF LEISEN das Doppelspalt – Experiment ein didaktischer
Alleskönner:
„Kurzum: Im Doppelspaltexperiment ‚steckt’, was in der Quantenphysik erstrangig ist.
Damit wird natürlich nicht behauptet, dass die Quantenphysik nur das ausMACHt, was
im Doppelspaltexperiment steckt, sondern dass man am Doppelspaltexperiment unter
dem Gesichtpunkt des Exemplarischen viele zentrale Inhalte und Fragen der
Quantenphysik
behandeln kann. Damit wäre
didaktischer Alleskönner.“
das
Doppelspaltexperiment ein
[Le02, S. 6]
Das JÖNSSON – Experiment (Abschnitt 3.2.2) und das TAYLOR – Experiment
Abschnitt 3.2.1) fungieren unter didaktischem Aspekt als Schüsselexperimente,
welche die Quantenphänomene „ganz lassen“, im Gegensatz zum Photoeffekt
(Abschnitt 2.3), der nur die Quantelung bestätigt, oder dem YOUNG – Experiment
(Abschnitt 2.1), welches nur das ‚wellige’ Verhalten zeigt. Somit kann ein adäquates
Verständnis von Quantenphänomenen aufgebaut werden, wenn ‚Welliges’,
‚Körniges’ und ‚Stochastisches’ „ganz gelassen und von Anfang an mitgedacht
werden“ [Le02, S.8].
Die Umsetzung der oben erwähnten Charakteristika der Quantenphysik wird im
Folgenden beschrieben. Ein weiterer Wesenszug der Quantenphysik, der am
Doppelspalt – Experiment gezeigt werden kann, ist die HEISENBERGsche
Unbestimmtheitsrelation, auf welche allerdings im Schülerlabor nicht eingegangen
wird.
5.5. Erster Tag des Schülerlabors
5.5.1 Der einführende Vortrag
Der Vortrag (Anhang C3) beginnt mit einer Motivation für die Beschäftigung mit
Quantenphysik, wobei die technischen Anwendungen wie Quantenkryptographie,
Quantenteleportation oder Quantencomputer im Vordergrund stehen. Durch die
Motivation mit Hilfe der technischen Anwendungen von Quantenphysik wird schon
73
zu Beginn ein Gefühl für die Kuriosität der Quantenphysik sensibilisiert. Es folgt
eine historische Entwicklung zur Entstehung der Quantenphysik, um die
quantenphysikalische Revolution zu skizzieren. In den historischen Teil sind die
wichtigsten physikalischen Inhalte von Licht im Wellenmodell (Interferenz,
Polarisation, Licht als elektromagnetische Welle) eingebettet. Die Entdeckung von
HALLWACHS, HERTZ und LENARD (Abschnitt 2.1) wird angesprochen, um somit einen
direkten Bezug zum folgenden Experiment, dem Photoeffekt, herzustellen. Der
Photoeffekt (Abbildung 43) wird an dieser Stelle zur Auflockerung des Vortrags
durchgeführt und bietet auch die Möglichkeit zur aktiven Beteilung der Schüler.
Abb. 43: Experimentelle Anordnung zum Photoeffekt
Sichtbares Licht (Glühbirne) bzw. UV – Licht treffen auf eine Fotozelle mit einer
Kaliumanode und der Photostrom (ausgelöste Elektronen) zwischen Kathode und
Anode wird mit Hilfe eines Messverstärkers gemessen. Bei sichtbarem Licht zeigt
das Messgerät keinen Stromfluss an, selbst wenn die Lichtintensität erhöht wird.
Auch bei längerem Warten ist kein Ausschlag des Messgerätes zu beobachten.
Wird die Fotozelle allerdings mit UV – Licht bestrahlt, so ist sofort ein Ausschlag
des Messgeräts zu erkennen, ein Strom fließt. Das bedeutet, dass durch das UV –
Licht Elektronen ausgelöst werden können, im Gegensatz zu sichtbarem Licht
74
(ohne UV – Anteil). Die Beobachtung lässt Rückschlüsse auf eine Grenzfrequenz
zu, ab der die Elektronen ausgelöst werden. Falls die Lichtintensität des UV –
Lichts erhöht wird, so ist ein proportionales Ansteigen des Photostroms zu
erkennen. Die Beobachtungen der Grenzfrequenz und der Proportionalität von
Lichtintensität (bei UV – Licht) und Photostrom können mit dem Wellenmodell von
Licht nicht erklärt werden. Die Schwierigkeiten, die das Wellenmodell besitzt, um
die Beobachtungen erklären zu können, werden explizit im Vortrag angesprochen.
Dadurch wird auf den Photoeffekt im praktischen Teil (Abschnitt 5.5.2.1) vorbereitet.
Im nächsten Abschnitt wird zum Ersten die Idee PLANCKs präsentiert, der ein
Energiequantum der Größe E = h
einführte, um die spektrale Verteilungsfunktion
eines schwarzen Körpers zu erklären (Abschnitt 2.2.1), und zum Zweiten wird dem
Energiequantum
ein
Impuls
zugeordnet,
um
so
die
Teilcheneigenschaft
hervorzuheben. Es wird so die Basis für die quantitative Erklärung (2.14) des
photoelektrischen Effekts gelegt, welche im praktischen Teil herausgefunden
werden soll. Die Einführung des Impulses eines Energiequantums wird ebenfalls
zum Erklären der Elektronenbeugung (Abschnitt 5.5.2.3) benötigt. Weiter muss eine
Einführung in die Röntgenbeugung gegeben werden, damit die BRAGG – Reflexion
angesprochen werden kann. Dadurch können die Interferenzeffekte und die
Beugungsringe verstanden werden. Als technische Anwendung wird hier die
Kristallstrukturanalyse mittels LAUE – Diagramme vorgestellt und das DEBYE –
SCHERRER – Verfahren kurz präsentiert. Es werden alle physikalisch relevanten
Inhalte behandelt, die für die selbständige Bearbeitung der Arbeitsblätter der
einzelnen Stationen (Abschnitt 5.5.2) nötig sind. Damit die Schüler die Inhalte des
Vortrags nachschlagen können gibt es ein Handout (Anhang C5).
5.5.2 Die Experimente des Stationenlernens
Die Experimente der einzelnen Stationen wurden so konzipiert, dass die Schüler
selbstständig die physikalischen Interpretationen der Beobachtungen geben sollen.
Einerseits werden die Schüler dadurch stark herausgefordert, andererseits kommt
dem Experiment eine methodische Schlüsselrolle als Teil des Erkenntnisprozesses
zu. So kann das Schülerinteresse gesteigert werden und Lernprozesse und
75
Einsichten gefördert werden [Eu05]. Die Arbeitsblätter des Stationenlernens sind in
Anhang C1 hinterlegt.
5.5.2.1 Der Photoeffekt
Die Versuchsanordnung ist von der Firma PASCO scientific [Pas07] und in
Abbildung 45 dargestellt. Die Quecksilberdampflampe enthält fünf verschiedene
Spektrallinien (Abbildung 46), die durch eine Gitterlinse spektral zerlegt werden. Die
fünf Spektrallinien werden nacheinander auf den Schlitz im weißen Schirm
gerichtet, so dass die Spektrallinien im Gehäuse auf die Fotozelle treffen und dort
Elektronen aus der Kathode (Abbildung 44) auslösen.
Kathode
Anode
Abb. 44: Gegenfeldmethode
Ziel dieses Versuchs ist die Messung der kinetischen Energie der ausgelösten
Elektronen in Abhängigkeit der eingestrahlten Frequenz des Lichts, um somit
sukzessive die Gleichung aus Abschnitt 2.3:
E Kin = h
-P,
(5.1)
zu erarbeiten. EKin ist die kinetische Energie der Elektronen und P ist die
Austrittsarbeit der Elektronen. Die kinetische Energie wird in der Regel mit Hilfe der
sogenannten Gegenfeldmethode (Abbildung 44) bestimmt. Werden Elektronen
durch eine Spannung U beschleunigt, so besitzen sie die kinetische Energie
E Kin = e U (e = Elementarladung). Umgekehrt können aber auch Elektronen, die
76
eine kinetische Energie E Kin durch Energiezufuhr erhalten haben, durch eine
entsprechende
Spannung
(Gegenspannung)
abgebremst
werden.
Dieser
Sachverhalt wird im Wesentlichen bei der Gegenfeldmethode ausgenutzt. Das Licht
überträgt seine Energie an die Elektronen, die dadurch aus dem Metall geschlagen
werden und somit eine gewisse kinetische Energie besitzen. Die aus dem Metall
(Kathode, Abbildung 44) tretenden Elektronen verursachen einen Strom, der mit
einem Ampèremeter gemessen werden kann. Möchte man nun die kinetische
Energie der Elektronen bestimmen, muss man mit dem Schiebewiderstand die
Spannung so einstellen, dass kein Strom mehr fließt. Wenn kein Strom mehr fließt,
bedeutet dies, dass keine Elektronen die Anode erreichen. Diese Spannung ist
somit unsere Gegenspannung U 0 aus der man die kinetische Energie E Kin = e U 0
erhält [Gre98]. Diese Methode wird bei dem Versuchsaufbau von PASCO scientific
in etwas abgewandelter Form benutzt. Die Spannung U 0 muss nicht eingestellt
werden, sondern wird direkt angezeigt, da ein Kondensator benutzt wird. Somit
können die Schüler den Spannungswert U 0 direkt ablesen.
Quecksilberdampflampe
Gehäuse mit Fotozelle
Schlitz
Gitterlinse
Messgerät
Zerotaster
Filter
Abb. 45: Versuchsaufbau zum Photoeffekt
77
Abb. 46: Frequenzen und Wellenlängen
Da nach einer Messung noch Restladungen auf dem Kondensator vorhanden sein
können, muss vor jeder Messung der Zerotaster (Abbildung 45), für einen
Nullabgleich, gedrückt werden. Außerdem müssen bei der Messung der grünen und
gelben Spektrallinie die entsprechend farbigen Filter vor dem Schlitz angebracht
werden. Die Filter begrenzen zum einen den Anteil höherer Lichtfrequenzen des
Umgebungslichts, die sich den gelben oder grünen Spektrallinien überlagern
können und somit die Messewerte verfälschen und zum anderen wird ultraviolettes
Licht aus Spektren höherer Ordnung zurückgehalten um so eine Überlagerung mit
den gelben und grünen Spektrallinien der Spektren niedriger Ordnung zu
vermeiden. Nach Aufnahme der Daten werden sie in ein Koordinatensystem
gezeichnet
und
Koordinatensystem
eine
Ausgleichsgerade
schon
vorskaliert
hindurchgelegt,
wobei
ist, um einem unnötigen
das
Zeitverlust
vorzubeugen. In dem Versuchsaufbau von PASCO scientific wird eine Kalium –
Natrium – Antimon Verbindung als Kathodenmaterial eingesetzt. Zusätzlich werden
noch Messungen einer Zink – Kathode bereitgestellt, die ebenfalls in das
Koordinatensystem gezeichnet werden. Auch bei den Daten der Zink – Kathode
wird wieder eine Ausgleichsgerade gezeichnet. Durch Vergleich beider Geraden
sollen die Schüler herausfinden, dass beide Geraden parallel sind, aber einen
unterschiedlichen Y – Achsenabschnitt besitzen, und anschließend sollen die
Funktionsgleichungen beider Geraden aufgestellt werden. Als nächstes sollen die
Schüler herausfinden, dass die Nullstelle der Geraden die Bedeutung einer
Grenzfrequenz hat und der Y – Achsenabschnitt die Austrittsarbeit darstellt, um die
Elektronen aus dem jeweiligen Kathodenmaterial auszulösen. Somit ist alles Nötige
vorhanden um mit der Idee des Energiequantums von PLANCK die Beobachtung
physikalisch zu interpretieren und einen quantitativen Zusammenhang (5.1)
herzustellen.
78
Um die Größenordnung der versuchsrelevanten physikalischen Größen zu
bestimmen, wurde die folgende Messung durchgeführt, wobei die Fehler der
Spannungswerte sich aus der Summe: Letzte Nachkommastelle des Messgerätes
± 1 und 0,9% Messungenauigkeit laut Hersteller ergeben. Somit ergibt sich der
Fehler für die kinetische Energie:
E Kin = e
U . Außerdem sind die Frequenzen
ohne Fehlerangaben seitens des Herstellers angegeben, so dass im Fall der
Frequenzen keine Fehler angegeben werden können. Bevor der Spannungswert
notiert wurde, musste ca. eine halbe Minute gewartet werden, bis sich der
Messwert stabilisiert hatte. Die Messdaten sind in Tabelle 1 dargestellt.
Frequenz [ 1014 Hz ]
Spannung [V]
EKin [ 10 !19 J ]
8,20
1,804
2,89
2,76
7,41
1,498
2,40
2,32
6,88
1,286
2,06
2,01
5,49
0,730
1,17
1,21
5,19
0,634
1,01
1,07
EKin [ 10 !21 J ]
Tab. 1: Messdaten zum Photoeffekt
Die lineare Regression wurde mit dem Programm Origin 7.5 erstellt und in
Abbildung 47 sind die Werte für h und P dargestellt, wobei A = P und B = h ist (5.1).
Da die Fehler für die Frequenzen fehlen, ist leider keine Aussage über die
Genauigkeit der Werte h und P möglich, lediglich die Abweichung vom Literaturwert
h = 6,6260693
10-34 Js kann angegeben werden. Es liegt eine relative Abweichung
vom Literaturwert von 5,7% vor. Die Schüler haben allerdings nicht die Möglichkeit,
ein Auswertungsprogramm zu benutzen, so dass die Abweichungen bei einer
graphischen Auswertung von ‚Hand’ höher sind. Trotzdem ist die Abweichung von
5,7% im Rahmen der Schulphysik als gering einzustufen. Die Interpretation des
Photoeffekts stützt das Teilchenmodell des Lichts, aber der nächste Versuch, das
Doppelspalt – Experiment mit Licht hoher Intensität, ist im Rahmen des
Wellenmodells von Licht erklärbar.
79
Messdaten aus Tabelle 1
Lineare Regression der Messdaten aus Tabelle 1
-19
3,0x10
-19
EKin [J]
2,5x10
-19
2,0x10
Linear Regression for Tabelle1:
Y=A+B*X
Weight given by Tabelle1 error bars.
-19
1,5x10
Parameter
Value
Error
-----------------------------------------------------------A
-2,24144E-19
-B
6,24922E-34
7,23267E-36
------------------------------------------------------------
-19
1,0x10
14
5,0x10
14
5,5x10
14
6,0x10
14
6,5x10
14
7,0x10
14
7,5x10
14
8,0x10
14
8,5x10
Frequenz [Hz]
Abb. 47: h – Bestimmung durch den Photoeffekt
5.5.2.2 Das Doppelspalt – Experiment
Im ersten Teil dieser Station soll der Spaltabstand des Doppelspalts bestimmt
werden und auch darüber hinaus soll eingeschätzt werden, ob der gemessene
Spaltabstand realistisch ist.
Schirm
Doppelspalt
Laser
Abb. 48: Versuchsaufbau zum Doppelspalt – Experiment
80
Außerdem bietet sich an dieser Stelle auch eine qualitative Sensibilisierung für
Fehlerbetrachtungen an. Der Versuchsaufbau ist sehr übersichtlich und in
Abbildung 48 dargestellt.
Die Maxima n –ter Ordnung sind gegeben durch (Abschnitt 2.1):
b sin
n
=n
(5.2)
mit n = 1, 2, 3, … .
Abstand Schirm – Doppelspalt
e
b
Maximum
0. Ordnung
H
H
Abstand
d
Maximum
1. Ordnung
Schirm ist weit entfernt
Schirm
Abb. 49: Bestimmung des Spaltabstands
Aus Abbildung 49 erhält man die Beziehung tan
=
d
und mit n = 1 folgt durch
e
Einsetzen von (5.2):
d
+
=
e
b
wobei die Näherung tan
- sin
, b=
e
,
d
(5.3)
für kleine Winkel benutzt wird.
Die Wellenlänge des Lasers beträgt
= 632,8 nm und wird ohne Fehler
angenommen, da der Fehler im Vergleich zu den anderen Messfehlern
81
vernachlässigbar gering ist. Für den Abstand Schirm – Doppelspalt erhält man e =
(110 ± 2) cm und für den Abstand Maximum 0. Ordnung und Maximum 1. Ordnung
erhält man d =
(0,3 ± 0,1) cm.
(0,23 ± 0,08) mm,
wobei der Fehler für den Spaltabstand über GAUßsche
Aus (5.3) ergibt sich für den Spaltabstand b =
2
Fehlerfortpflanzung berechnet wird:
2
' e$ 'e d $
% " +% 2 " .
& d # & d #
b=
Da keine Herstellerangaben bezüglich des verwendeten Doppelspalts vorhanden
waren, wurde der Doppelspalt unter einem Mikroskop vermessen zu: b =
(0,22 ± 0,02) mm.
Die Messmethode über den Doppelspalt ist zwar recht ungenau,
liefert aber die richtige Größenordnung und ist somit im Rahmen dieses
Schülerlabors als akzeptabel zu beurteilen.
Für den zweiten Teil dieser Station wird die Doppelspalt – Simulation (Abschnitt
5.6.2.1) verwendet. Das Doppelspalt – Experiment wird mit Kugeln (klassische
Teilchen)
durchgeführt
Intensitätsverteilungen
und
beider
soll
die
Einzelspalte
Erkenntnis
einfach
liefern,
addiert
dass
werden
die
können
(Abschnitt 3.2.2). Im nächsten Schritt wird der Doppelspalt mit Elektronen
beschossen (Abschnitt 3.2.2). Hierzu werden zwei Versionen der Arbeitsblätter
ausgegeben. Zum einen wird eine Version ausgeteilt, falls die Schüler die
Elektronenbeugung (Station 3 bzw. Abschnitt 5.5.2.3) noch nicht durchgeführt
haben, und zum anderen eine Version, falls die Schüler die Elektronenbeugung
schon durchgeführt haben. Falls die Schüler noch nicht wissen, dass Elektronen
eine
Wellenlänge
zugeordnet
werden
kann
(keine
Elektronenbeugung
durchgeführt), sollen lediglich die Widersprüche zur klassischen Physik skizziert
werden. Der Widerspruch liegt im Beobachten von Interferenzminima, welche
klassisch nicht zu erklären sind. Da die Schüler vorher untersucht haben, welches
Verhalten klassische Teilchen zeigen, ist das notwendige Wissen vorhanden, um
diesen Aufgabenteil zu bearbeiten. Falls die Elektronenbeugung schon behandelt
wurde, sollen die Schüler sich lediglich bewusst sein, wo der Widerspruch liegt, und
mit Hilfe der Wellenlänge von Elektronen die Interferenzminima erklären. Die
Erklärung der Interferenzminima wird nicht explizit durch eine Anweisung auf dem
Arbeitsblatt gefordert, sondern soll durch Nachfragen des Betreuers erfolgen. Somit
schärft diese Station die Betrachtung für das ‚Wellige’ bei Licht, und für das
‚Körnige’ und das ‚Wellige’ bei Quantenobjekten (Elektronen). Da diese
82
Betrachtungen, bis auf den Wellencharakter von Licht, nur in Form einer Simulation
erarbeitet werden können, wird als dritte Station die Elektronenbeugung als
Realexperiment durchgeführt.
5.5.2.3 Die Elektronenbeugungsröhre
In diesem Versuch soll der Zusammenhang
Elektronen)
durch
Arbeitsaufträge
=
h
(Abschnitt 2.4) für Materie (hier
p
sukzessive
erarbeitet
werden.
Der
Versuchsaufbau ist in Abbildung 50 dargestellt. Die Elektronenbeugungsröhre ist im
Querschnitt in Abbildung 51 dargestellt.
Elektronenbeugungsröhre
Messgerät für Heizstrom
Netzgerät für Beschleunigungsspannung
(Hochspannung)
Netzgerät für Heizwendel
(Elektronenquelle)
Abb. 50: Versuchsaufbau zur Elektronenbeugung
83
Abb. 51: Schematische Darstellung der Elektronenbeugungsröhre
In diesem Versuch wird die Elektronenbeugung an stochastisch verteilten
Graphitkristallen
(Einzelkristalle)
durchgeführt
(Abschnitt
2.5).
Als
Auswertungsverfahren dient das DEBYE – SCHERRER – Verfahren, welches
ermöglicht, die Wellenlänge der Elektronen bei bekannten Gitterabständen des
Graphits über die Ringdurchmesser zu bestimmen. Der Impuls der Elektronen wird
über die Beschleunigungsspannung ermittelt. Die Elektronen werden durch ein
Potential UB beschleunigt und treffen auf den Graphitkristall (Abbildung 51). Der
Impuls der Elektronen beträgt demnach:
p = 2m e e
UB ,
(5.4)
wobei me die Masse und e die Ladung des Elektrons ist. Die Elektronen werden
unter der BRAGGschen Bedingung
2
d sin
=n
(5.5)
am Kristallgitter mit dem Gitterabstand d in ein Maximum n-ter Ordnung gebeugt.
Durch die stochastische Anordnung der Einzelkristalle entsteht eine Ringstruktur.
Im Weiteren sei n = 1. Man beobachtet allerdings zwei Beugungsringe 1. Ordnung
84
in
diesem
Versuch.
Dies
rührt
daher,
dass
es
zwei
Netzebenen
mit
unterschiedlichen Gitterabständen d1 und d2 gibt, an denen die BRAGG – Reflexion
auftritt.
Abb. 52: Netzebenenabstand von Graphit
Die Netzebenenabstände von Graphit sind in Abbildung 52 zu sehen. Falls der
Netzebenenabstand d und die Ordnung n der Ringe bekannt sind, so kann man
über die Ringradien R die Wellenlänge bestimmen (Abbildung 51):
tan(2 ) =
R
.
L
Benutzt man die Nährung 2 sin( ) - tan(2 ) für kleine Winkel
R
.
2L
-
sin
(5.6)
, so erhält man:
(5.7)
Durch Einsetzen von (5.7) in die BRAGG – Bedingung (5.5) mit n = 1 erhält man:
=
d
R
L
.
(5.8)
Für mehr Informationen bezüglich der BRAGG – Bedingung oder des DEBYE –
SCHERRER – Verfahrens wird auf den Anhang C1, C3 und C5 verwiesen. Auf dem
Arbeitsblatt zu diesem Versuch wird dem Schüler das Messverfahren erläutert. Als
Erstes soll der Schüler die Beugungsringe bei eingestellter Spannung von 3000V
85
beobachten. Im Einführungsvortrag wurde die Ringstruktur bei eingestrahlter
Röntgenstrahlung thematisiert, so dass ein erster Konflikt bei der Beobachtung von
Ringstrukturen in diesem Experiment entstehen soll. Die Schüler sollen sich fragen:
Warum erhält man beim Beschuss des Graphitkristalls mit Teilchen (Elektronen) ein
wellentypisches Interferenzmuster? Dadurch werden die folgenden Aufgabenteile
motiviert. Im weiteren Verlauf sollen die Schüler testen, ob es sich nach Durchgang
der Elektronen durch den Kristall um Elektronen oder elektromagnetische Strahlung
handelt, die auf dem Beobachtungsschirm auftrifft. Dies wird mit einem Magneten
untersucht, damit eindeutig bestätigt werden kann, dass Elektronen auf den Schirm
treffen. Da die Schüler sich nun bewusst sein sollten, dass es sich bei diesem
Experiment um Elektronenbeugung handelt, wird nun nach einer physikalischen
Interpretation gesucht, indem die Wellenlänge und der Impuls gemessen wird, um
so den funktionalen Zusammenhang
(p )
zu ermitteln. Die Schüler tragen die
Wellenlänge über den Kehrwert des Impulses auf, um so die Steigung als
PLANCKsches Wirkungsquantum zu identifizieren. Dies sollte möglich sein, da die
Gleichung
=
h
aus dem Einführungsvortrag bekannt ist. Zum Schluss sollen die
p
Schüler nun auf Grund der zugeordneten Materiewelle den Beugungseffekt
erläutern.
Damit auch bei diesem Versuch die Größenordnung der Messergebnisse
abgeschätzt werden kann, wurde eine Messreihe (Tabelle 2), wie die Schüler sie
aufnehmen, erstellt. L ist in diesem Versuch laut Hersteller 13,5 cm.
Netzebenenabstand
d1 = 0,123·10-9m
(großer Ring)
Netzebenenabstand
d2 = 0,231·10-9m
(kleiner Ring)
Impuls
Spannung
[V]
Durchm
[cm]
Radius
[cm]
Wellenlänge
[ 10 !11 m]
Durchm
[cm]
Radius
[cm]
Wellenlänge
[ 10 !11 m]
10 ! 23 kg
2000
3000
4000
5000
6,2
5,2
4,5
4
3,1
2,6
2,25
2
2,82
2,37
2,05
1,82
3,8
3,0
2,6
2,3
1,9
1,5
1,3
1,15
3,00
2,37
2,05
1,81
2,41
2,96
3,42
3,82
Tab. 2: Messdaten zur Elektronenbeugung
86
m
s
Da der Schirm gewölbt ist und mit einem normalen Metermaß die Durchmesser
vermessen wurden, musste ein Fehler von 0,4cm für die großen Ringe und 0,3cm
für die kleinen Ringe angenommen werden. Ein kleinerer Fehler bei den kleineren
Ringen ergibt sich aus der geringeren Krümmung des Schirms. Für die Fehler der
± 1 des
Spannung wurde die Summe aus der letzten Nachkommastelle
Anzeigegerätes der Hochspannungsquelle und der Messunsicherheit von 1%
=
angenommen. Der Fehler für die Wellenlänge ergibt sich aus
Fehler für die Impulskehrwerte aus
1
1
1' 1 $
=
%
"
- 25
p 5,4 10 2 %& U "#
d
L
R und der
3
U , wobei die
Einheiten beim Vorfaktor weggelassen wurden. Wenn die Einheit Volt eingesetzt
wird, erhält man auch die Grundeinheit für den Impuls.
In Tabelle 3 befinden sich die für die graphische Auswertung nötigen Daten des
kleinen Rings und analog in Tabelle 4 die des großen Rings.
1
s
10 22
p
kg m
1
p
10 20
s
kg m
[ 10
!11
m
]
[ 10
!12
4,14
12,4
3,00
2,37
3,38
7,33
2,37
2,37
2,93
5,12
2,05
2,37
2,62
3,93
1,81
2,37
m
]
m
]
Tab. 3: Messdaten des kleinen Rings
1
s
10 22
p
kg m
1
p
10 20
s
kg m
[ 10
!11
m
]
[ 10
!12
4,14
12,4
2,82
1,82
3,38
7,33
2,37
1,82
2,93
5,12
2,05
1,82
2,62
3,93
1,82
1,82
Tab. 4: Messdaten des großen Rings
87
[m]
3,2x10
-11
3,0x10
-11
2,8x10
-11
2,6x10
-11
2,4x10
-11
2,2x10
-11
2,0x10
-11
1,8x10
-11
Daten aus Tabelle3
Lineare Regression für Tabelle 3
Linear Regression für Tabelle3:
Y=A+B*X
Parameter
Value
Error
-----------------------------------------------------------A
-2,24465E-12
6,85473E-12
B
7,74964E-34
2,06654E-34
-----------------------------------------------------------22
22
22
22
22
22
22
22
22
2,6x10 2,8x10 3,0x10 3,2x10 3,4x10 3,6x10 3,8x10 4,0x10 4,2x10
1/p [s/kg*m]
Abb. 53: h – Bestimmung durch Elektronenbeugung (kleiner Ring)
Daten aus Tabelle 4
Lineare Regression für Tabelle 4
-11
3,0x10
-11
2,8x10
-11
[m]
2,6x10
-11
2,4x10
Linear Regression für Tabelle 4
Y=A+B*X
Parameter
Value
Error
-----------------------------------------------------------A
1,22655E-12
5,27782E-12
B
6,56137E-34
1,59114E-34
------------------------------------------------------------
-11
2,2x10
-11
2,0x10
-11
1,8x10
22
22
22
22
22
22
22
22
22
2,6x10 2,8x10 3,0x10 3,2x10 3,4x10 3,6x10 3,8x10 4,0x10 4,2x10
1/p [s/kg*m]
Abb. 54: h – Bestimmung durch Elektronenbeugung (großer Ring)
Man erhält zwei Diagramme, jeweils eins für den kleinen Ring (Abbildung 53) und
eins für den großen Ring (Abbildung 54). Die lineare Regression wurde mit Origin
88
7.5
Pro
durchgeführt.
Der
Parameter
B
entspricht
dem
PLANCKschen
Wirkungsquantum h in Abbildung 53 und 54. Man erkennt ganz deutlich, dass die
Messmethode im Gegensatz zum Photoeffekt wesentlich ungenauer ist. Die
Auswertung des kleinen und des großen Rings werden innerhalb der Gruppe
aufgeteilt, so dass auch bezüglich der Unterschiede beider Ausgleichsgeraden die
Möglichkeit zur Diskussion besteht. Die Größenordnung der Messergebnisse in
diesem Versuch ist somit im Rahmen dieses Schülerlabors akzeptabel für die
Bestimmung des PLANCKschen Wirkungsquantums.
5.6 Zweiter Tag des Schülerlabors
5.6.1 Der einführende Vortrag
Der Einführungsvortrag (Anhang C4) am zweiten Tag des Schülerlabors steht unter
dem Motto ‚Des Rätsels Lösung’ und soll den ‚Welle’ oder ‚Teilchen’ Konflikt im
einheitlichen Bild der Wellenfunktion auflösen. Zuerst werden die Ergebnisse der
Experimente
des
Stationenlernens
(Abschnitt
5.5.2)
in
einem
gelenkten
Unterrichtsgespräch erarbeitet und die wichtigsten Ergebnisse kurz diskutiert und
festgehalten. Dabei bildet das JÖNSSON – Experiment den Abschluss dieser
Versuche, um direkt zur folgenden Frage überzuleiten: Verhalten sich auch
einzelne Photonen (TAYLOR – Experiment in Abschnitt 3.2.1) beim Durchgang durch
einen Doppelspalt wie die Elektronen? Um dieser Frage nachzugehen, wird ein
Doppelspalt – Experiment mit einzelnen Photonen eingesetzt. Dieses Experiment
wurde im Rahmen einer Staatsexamensarbeit von CHRISTIAN VOGL an der
Universität Mainz entwickelt. Für die genaue Funktionsweise dieses Experiments
wird auf die Staatsexamensarbeit [Vo03] von CHRISTIAN VOGL verwiesen. Somit
kann den Schülern auch ein Realexperiment zum Welle – Teilchen – Dualismus
gezeigt werden, um dem Vorurteil vorzubeugen, dass Simulationen nur zeigen, was
programmiert wird, und so die Realität manipulierbar ist. Auch andere
Quantenobjekte wie Helium, Neutronen, Fullerene, … zeigen Interferenz beim
Durchgang durch den Doppelspalt. Das Problem ist allerdings ein Modell zu finden
was beides beschreibt, denn weder das Wellenmodell noch das Teilchenmodell
89
vermag
alle
Aspekte
des
Doppelspalt
–
Experiments
mit
einzelnen
Quantenobjekten zu erklären. Um beide Aspekte zu beschreiben wird die
Wellenfunktion eingeführt und das Superpositionsprinzip (Abschnitt 3.2.2) am
Doppelspalt verdeutlicht, wobei auf die zwei wichtigen Wesenszüge der
Quantenphysik eingegangen wird: zum einen dem statistischen und nicht
vorhersagbaren Auftreffen einzelner Quanten (Abschnitt 3.2.1) auf dem Schirm und
zum anderen, unter welcher Bedingung Interferenz eintritt (Abschnitt 3.2.2).
Allerdings
wird
die
Wellenfunktion
nicht
als
komplexe
Funktion
beim
Superpositionsprinzip behandelt, sondern als reelle Funktion, wodurch sich
folgender Interferenzterm (siehe Abschnitt 3.2.2) ergibt:
2
1
(x )
2
(x ) .
(5.9)
Im Rahmen dieses Schülerlabors soll diese didaktische Reduktion jedoch kein
Problem darstellen und es kann auf den komplexen Interferenzterm verzichtet
werden. Bevor die Inhalte der Gruppenphase (Abschnitt 5.6.2) thematisiert werden,
wird zur Festigung des Inhalts eine kurze Zusammenfassung der wichtigsten
Formeln und Beobachtungen gegeben. Auf die Inhalte der Gruppenphase wird zum
einen aufmerksam gemacht und zum anderen werden auch physikalische Aspekte
der Inhalte angesprochen. Beim MACH – ZEHNDER – Interferometer wird die
Interferenz in den verschiedenen Detektoren/Schirmen (Abschnitt 3.3.2.1) erklärt,
um eine einheitliche Wissensbasis bei den Präsentationen zu schaffen. Um auf den
Quantenradierer (Kapitel 4) vorzubereiten, wird die ‚Welcher – Weg’ – Markierung
von Photonen mittels Polarisationsfiltern erläutert. Zum Schluss werden die Schüler
am
Beispiel
des
Indeterminismus
der
Quantenmechanik
in
die
Interpretationsproblematik eingeführt. Es wird erklärt, was verborgene Parameter
sind, um somit wieder eine einheitliche Wissensbasis zu schaffen. In Anhang C6 ist
das Handout dieses Vortrags zu finden.
90
5.6.2 Die Experimente der Gruppenphase
Die Arbeitsblätter der Experimente der Gruppenphase befinden sich in Anhang C2.
Diese Phase kennzeichnet sich aus durch eine Arbeit in Kleingruppen, wobei es
drei Gruppen gibt und jede sich mit einem anderen Thema auseinandersetzt. Eine
Gruppe beschäftigt sich mit dem MACH – ZEHNDER – Interferometer. Diese Schüler
betrachten den Quantenradierer (Kapitel 4) als auch die ‚wechselwirkungsfreie
Messung’ (Abschnitt 3.4). Die beiden anderen Gruppen beschäftigen sich im ersten
Teil der Gruppenarbeit mit denselben Inhalten: der Komplementarität (Abschnitt
3.2.3) am Doppelspalt. Die Vermittlung der Komplementarität ist das gemeinsame
Lernziel aller drei Versuchsblöcke, damit sich dieses fundamentale Prinzip der
Quantenphysik einprägt. Nach der Komplementarität beschäftigen sich diese
Schüler mit zwei unterschiedlichen Interpretationen der Quantenmechanik. Eine
Gruppe übernimmt die Kopenhagener Deutung (Abschnitt 3.5.1) und die andere
Gruppe setzt sich mit der BOHMschen Interpretation der Quantenmechanik
(Abschnitt 3.5.2) auseinander. Die Gruppenphase bietet sehr viel Raum für
Diskussionmöglichkeiten durch die Thematik der ‚wechselwirkungsfreien Messung’
und den Interpretationsrichtungen der Quantenmechanik, womit eine interessante
Arbeitsatmosphäre geschaffen werden soll. Anschließend sollen sich die Schüler
auf die Präsentation vorbereiten, wobei hier stichwortartige Hilfestellungen gegeben
werden. Die Präsentationen dienen einmal zum Wissensaustausch der einzelnen
Gruppen und zum anderen der Schülerlaborleitung zur Verständnisüberprüfung,
denn nur auf einem guten Verständnis der Thematik kann eine adäquate
Präsentation erfolgen. Bevor die Experimente der Gruppenphase (Abschnitt 5.6.2.2
bis 5.6.2.4) genauer beschrieben werden, erfolgt eine kurze Vorstellung der
Simulationen (Abschnitt 5.6.2.1), die in der Gruppenphase als Experimentiertisch
dienen. Lediglich der Quantenradierer kann als Realexperiment vorgeführt werden.
Die Präsentationen der experimentellen Ergebnisse finden mit Hilfe der
Simulationen statt. Als Medien dienen somit Computer und Tafel, da an der Tafel
die Interpretationen der Quantenmechanik fixiert werden können.
91
5.6.2.1 Der Computer als Experimentiertisch
Doppelspalt – Experiment
Die Simulation des Doppelspalt – Experiments mit einzelnen Quantenobjekten
wurde von KLAUS MUTHSAM im Rahmen seiner Zulassungsarbeit am Lehrstuhl für
Didaktik an der Ludwig – Maximilians – Universität München entwickelt. Im
Folgenden werden die Parameter des Simulationsprogramms [Do99] anhand eines
Screenshots (Abbildung 55) aus der Simulation vorgestellt.
Objektquelle
Beobachtungslampe
Spalt
Schirm
Abb. 55: Screenshot aus der Simulation zum Doppelspalt – Experiment
Objektquelle
Als Objekte, die aus der Quelle emittiert werden, dienen in diesem Schülerlabor
Elektronen und Kugeln. Es gibt aber auch die Möglichkeit, andere Quantenobjekte
auf den Doppelspalt zu schießen: Photonen, Myonen, Farbspray, Heliumatome,
uvm.. Durch Betätigen des Buttons ‚Quelle’ (Abbildung 55: rechte untere Ecke)
92
können die einzelnen Quantenobjekte ausgewählt und die Energie der Objekte
eingestellt werden.
Spalt
Der Button ‚Blende’ (Abbildung 55: rechte untere Ecke) ermöglicht die Einstellung
der Spaltbreite und auch die Möglichkeit zur Auswahl zwischen Einzelspalt und
Doppelspalt. Im Falle der Wahl des Doppelspalts kann auch der Spaltabstand
variiert werden.
Beobachtungslampe
Die Lampe dient zur Ortsdetektion in der Spaltebene und somit zum Beobachten
der Komplementarität (Abschnitt 3.2.3) durch Photonenstreuung. Berücksichtigt ist
auch das Auflösungsvermögen der Lichtquelle. Die Beobachtungslampe wird über
den Button ‚Lampe’ (Abbildung 55: rechte untere Ecke) aktiviert und beinhaltet die
Variation der Lichtintensität und der Wellenlänge des ausgesandten Lichts.
Schirm
Auf dem Schirm werden die einzelnen Treffer markiert, so dass man die Möglichkeit
besitzt, das sich allmählich aufbauende Interferenzmuster zu beobachten. Ein
weiterer Vorteil bietet die Möglichkeit der Photographie von drei verschiedenen
Interferenzmustern und das gleichzeitige Darstellen dieser Fotos. Somit können die
Interferenzmuster verglichen werden, die entstehen, wenn jeweils nur ein Spalt
offen ist oder wenn beide Spalte offen sind. Weiterhin besitzt der Schirm eine
Zoommöglichkeit
und
die
Anzeige
der
theoretischen
Verläufe
der
Intensitätsverteilungen bzw. der Interferenzmuster.
MACH – ZEHNDER – Interferometer
Das Simulationsprogramm [Mz99] zum MACH – ZEHNDER – Interferometer wurde
von ALBERT HUBERT am Lehrstuhl für Didaktik an der Ludwig – Maximilians –
93
Universität München entwickelt. Ein Screenshot aus der Simulation ist in Abbildung
56 zu sehen. In der unteren Leiste in Abbildung 56 sind die einzelnen Funktionen
des Programms abgebildet, welche wieder unterteilt sind in ‚Instrumente’, ‚Quelle’,
‚Anzahl der Photonen’ und ‚Perspektive’ und im Folgenden genauer beschrieben
werden.
Abb. 56: Screenshot aus der Simulation zum MACH – ZEHNDER – Interferometer
Quelle
Aus der Quelle können zum einen einzelne Photonen, durch Anklicken von
‚Einzelne Photonen’ emittiert oder zum anderen, durch Anklicken von ‚Laser’, sehr
viele Photonen emittiert werden. Letzteres entspricht dem klassischen Fall von Licht
hoher Intensität und die Beobachtungen können mit dem Wellenmodell erklärt
werden.
Instrumente
Hier können Detektoren in die beiden Strahlwege gebracht werden und es kann
gezeigt werden, dass nie beide Detektoren ‚klicken’, da sich ein Photon nicht an
einem Strahlteiler teilt, sondern immer nur als ‚Ganzes’ den einen oder anderen
Strahlweg nimmt. Außerdem können drei Polarisationsfilter so in den Strahlengang
gebracht werden, dass sich der Aufbau eines Quantenradierers (Kapitel 4) ergibt.
94
Die Stellungen der Polarisationsfilter können über die komplette Winkelskala von
360° eingestellt werden.
Anzahl der Photonen
Die Anzahl der Photonen, die auf den Schirm treffen, werden angezeigt, ebenso die
Anzahl der emittierten Photonen. Die Photonen, die von den Detektoren detektiert
werden, werden auch gezählt.
Perspektive
Die Perspektive des Versuchsaufbaus kann variiert werden.
Bombentest – Experiment
Um die ‚wechselwirkungsfreie Messung’ (Abschnitt 3.4) zu verdeutlichen, wird als
Simulationsprogramm ein Java Applet von FRANZ EMBACHER verwendet, welches
unter [Wwm98] im Internet zu finden ist. Abbildung 57 zeigt einen Screenshot aus
dem Simulationsprogramm. Unter der Rubrik Strahlengänge wird bei Betätigen des
Buttons ‚Interferometer’ die Interferenz an den jeweiligen Detektoren angezeigt. Der
Button ‚mit Hindernis’ bringt ein Hindernis in den oberen Strahlengang und simuliert
die Interferenzen an den Detektoren, wenn ein Hindernis im Strahlengang ist. Unter
der Rubrik Klassische Theorie wird die Wellenvorstellung simuliert und die sich
daraus ergebenden Interferenzmuster mit und ohne Hindernis. Im Wesentlichen
zeigt diese Rubrik das Gleiche wie die Rubrik Strahlengänge, wobei explizit die
Welle dargestellt wird die sich durch das Interferometer bewegt. Unter der Rubrik
Quantentheorie befinden sich die notwendigen Buttons, um das Bombentest –
Experiment (Abschnitt 3.4) durchzuführen. Die Detektoren summieren ihre ‚Klicks’
jeweils auf, so dass eine statistische Aussage gemacht werden kann. Für eine
detailliertere Beschreibung wird auf [Wwm98] verwiesen. Durch Betätigen des
Buttons ‚Beschreibung’ erhält man mehr Informationen zu diesem Applet.
95
Abb. 57: Screenshot aus der Simulation zum Bombentest – Experiment
5.6.2.2 Das MACH – ZEHNDER – Interferometer
Die Schüler benutzen die Simulation zum MACH – ZEHNDER – Interferometer und
führen das Experiment mit einzelnen Photonen durch. Als Erstes sollen die Schüler
das Experiment ohne Polarisationsfilter durchführen und vorhersagen, welche
Beobachtung Sie machen. Sie sollen – den Einführungsvortrag des zweiten Tags
reflektierend – das ringförmige Interferenzmuster (Abschnitt 4.1) vorhersagen
können und ihre Vorhersagen auch überprüfen. Als Nächstes wird in jeden
Strahlengang ein Polarisationsfilter gestellt und vier verschiedene Messungen bei
vier verschiedenen Einstellungen der Polarisationsfilter durchgeführt, wobei die
Polarisationsfilter
parallel
ausgerichtet
sind.
Die
Beobachtung,
dass
das
Interferenzmuster nicht verschwindet, soll auf die folgenden Aufgabenstellungen
vorbereiten.
Es
soll
erkannt
werden,
dass
bei
gleicher
Stellung
der
Polarisationsfilter keine Aussage über den Weg der Photonen möglich ist.
Anschließend werden zwei Polarisationsfilter in gekreuzter Stellung (90° Winkel) in
den Versuchsaufbau gebracht und das Verschwinden des Interferenzmusters
96
beobachtet. Danach wird der Versuchsaufbau zum Quantenradierer ergänzt, indem
der dritte Polarisationsfilter in den Ausgang des MACH – ZEHNDER – Interferometers
gestellt wird. Auf Grund der Beobachtung, dass das Interferenzmuster wieder
sichtbar wird, sollen die Schüler das Komplementaritätsprinzip formulieren. Die
Schüler sollen als Abschluss dieses Blocks mit Hilfe der Detektoren testen, ob sich
ein
Photon
am
Strahlteiler
aufteilt.
Denn
sonst
könnte
man
das
Komplementaritätsprinzip versuchen zu erklären, in dem man annimt das sich ein
Photon am Strahlteiler aufteilt. Als zweiter Block folgt das Realexperiment zum
Quantenradierer (Kapitel 4). Die Schüler sollen die Beobachtungen aus der
Simulation am Realexperiment verifizieren und mit dem Betreuer über den
Versuchsaufbau, die Interferenzmuster, die Stellungen der Polarisationsfilter uvm.
Diskutieren, um einen Vergleich zwischen idealisiertem und realem Aufbau
anzustellen. Als letzter Block wird das Bombentest – Experiment (Abschnitt 3.4) mit
Hilfe
der
Simulation
‚wechselwirkungsfreie
von
FRANZ
Messung’
zu
EMBACHER
durchgeführt,
verdeutlichen.
Zuerst
um
wird
so
ein
die
kurzer
einleitender Text, welcher von [Osp07] übernommen wurde, zur Problemstellung
des Bombenstest – Experiments gelesen. Danach sollen die Schüler mit Licht als
Welle versuchen, das Hindernis zu detektieren. Das gelingt natürlich nicht und so
muss der Ausweg über die Quantentheorie gesucht werden, es müssen einzelne
Photonen benutzt werden. Die Schüler sollen mit Hilfestellung das Messprinzip
herausfinden, welches die Unterscheidung einer scharfen Bombe von einem
Blindgänger ermöglicht. Außerdem soll die Wahrscheinlichkeit für die Detektion
einer scharfen Bombe angegeben werden. Als letzter Punkt soll die Präsentation
vorbereitet werden.
5.6.2.3 Die Kopenhagener Interpretation der
Quantenmechanik
Im
ersten
Abschnitt
dieses
Arbeitsblatts
sollen
die
Schüler
sich
die
Komplementarität am Doppelspalt mit Hilfe der Simulation von KLAUS MUTHSAM
[D099] erarbeiten. Dazu werden Elektronen als Quelle benutzt und die Parameter
wie Energie der Elektronen und Spaltabstand vorgegeben. Zuerst sollen die
97
Schüler das Experiment ohne Beobachtungslampe durchführen und einen
Fotostreifen belichten. Danach wird die Lampe aktiviert und das Verschwinden des
Interferenzmusters beobachtet, wobei die Beobachtung wieder auf dem zweiten
Fotostreifen gespeichert wird. Nun werden die Schüler aufgefordert, auf Grund der
Beobachtungen das Komplementaritätsprinzip zu formulieren. Spalt 1 wird
geschlossen und das Experiment wird ohne Lampe durchgeführt. Nun wird Spalt 1
geöffnet und Spalt 2 geschlossen und wieder eine Messung durchgeführt. Beide
Bilder werden zusammen auf dem dritten Fotostreifen festgehalten. Die Schüler
sollen den dritten Fotostreifen mit dem zweiten Fotostreifen, auf dem die
Beobachtung des Komplementaritätsprinzips abgebildet ist, vergleichen und zu
dem Schluss kommen, dass beide Bilder identisch sind. Somit ist es gleichgültig, ob
man beobachtet, durch welchen Spalt ein Elektron tritt, oder das Experiment mit nur
einem Spalt durchführt und die Verteilung der Einzelspalte addiert. Als Lernkontrolle
werden die Schüler aufgefordert, zu den Interferenzmustern aus den vorigen
Aufgabenstellungen die Intensitätsverteilungen zu skizzieren. Da nun die
Intensitätsverteilungen vorliegen, sollen die Schüler durch einen Vergleich folgern,
was mit dem Interferenzterm (siehe Abschnitt 3.2.2) bei einer Ortsdetektion
geschehen
muss.
Der
Interfernzterm
muss
Null
werden,
um
die
Intensitätsverteilung bei einer Ortsdetektion zu erklären. Anschließend werden die
Schüler davon überzeugt, dass die Zusammenstöße der Photonen mit den
Elektronen nicht verantwortlich für das Verschwinden des Interferenzmusters sind.
Die Kopenhagener Interpretation (Abschnitt 3.5.1) wird auf der Basis eines
ausgeteilten Textes erarbeitet, der inhaltlich im Wesentlichen auf [Gri06] basiert.
Den Schülern werden die Kernaussagen der Kopenhagener Interpretation
stichwortartig vorgegeben und können dann mit Hilfe des Textes verstanden
werden. Die Kernaussagen werden vorgegeben, damit die Schüler nicht unwichtige
Aussagen des Textes als Kernaussage identifizieren und somit anschließend keine
adäquate Präsentation der Kernaussagen erfolgen kann. Da die Kopenhagener
Interpretation der Quantenmechanik auf erkenntnistheoretischem Wege entstanden
ist und eine der häufigsten dargestellten Interpretationsrichtungen ist, wird versucht
sie den Schülern zu vermitteln.
98
5.6.2.4 Die BOHMsche Interpretation der
Quantenmechanik
Der erste Teil des Arbeitsblatts ist identisch mit dem Arbeitsblatt zur Kopenhagener
Interpretation der Quantenmechanik, da die physikalischen Inhalte als wichtig
erachtet werden und somit eine bessere Festigung des Erlernten erfolgt. Alle
Schüler beschäftigen sich mit dem Komplementaritätsprinzip und zwei Gruppen
präsentieren das Komplementaritätsprinzip: Einmal am Doppelspalt (Gruppe, die
sich mit der Kopenhagener Interpretation der Quantenmechanik beschäftigt) und
zum zweiten am MACH – ZEHNDER – Interferometer. Des Weiteren übernimmt auch
die Gruppe, die sich mit der Kopenhagener Interpretation der Quantenmechanik
beschäftigt, die Präsentation der Ortsdetektion eines Elektrons (Abschnitt 3.2.3) in
der Spaltebene des Doppelspalts. Die Präsentation der Gruppe, die sich mit der
BOHMschen Interpretation der Quantenmechanik beschäftigt, beschränkt sich auf
die Erklärung, warum das Interferenzmuster nicht bei der Ortsdetektion durch den
Zusammenstoß eines Elektrons mit einem Photon verschwindet. Die Kernaussagen
der BOHMschen Interpretation werden wieder stichwortartig vorgegeben und anhand
eines ausgeteilten Textes erläutert. Die Texte basieren auf [Küb04] und [Wi07]. Die
BOHMsche Interpretation ist sehr schwer, dafür aber umso interessanter, weil sie
den Determinismus wieder in die Quantenmechanik zurückbringt. Die Schüler
könnten solch eine Anlehnung an die klassische Mechanik für durchaus
befriedigend und interessant empfinden. Dadurch wird es den Schülern ermöglicht
eine interessante Diskussion zu führen, bei der zwei völlig unterschiedliche
Interpretationsrichtungen der Quantenmechanik gegenüber gestellt werden.
5.7 Durchführung und zeitlicher Rahmen des
Schülerlabors
Das Schülerlabor wurde von einem Oberstufenkurs aus Hessen und aus Rheinland
– Pfalz besucht. Beide Oberstufenkurse waren Physik Leistungskurse und
bestanden aus jeweils 13 Schülern am Ende der Jahrgangsstufe 12. Die Schüler
99
waren an zwei aufeinander folgenden Tagen an der Universität Mainz zu Gast.
Beide Kurse waren jedoch zu unterschiedlichen Tageszeiten an der Universität
Mainz. Der Kurs aus Hessen war am 5./6. Juni anwesend und folgte dem Zeitplan
in Tabelle 5 . Der Tagesablauf des Oberstufenkurses aus Rheinland – Pfalz, der am
26./27. Juni am Schülerlabor teilnahm, ist in Tabelle 6 zu sehen. Die Zeit für den
Einführungsvortrag am ersten Tag war mit einer Stunde in beiden Fällen (Hessen
und Rheinland – Pfalz) durchaus angemessen. Die Gruppengrößen ergaben sich
aus der Gesamtanzahl der Schüler zu vier bis fünf Schülern pro Gruppe. Für das
Stationenlernen wurden beim erstmaligen Durchführen 55min pro Station
eingeplant mit einer kurzen Pause von 5min zum Wechseln der Stationen.
Zeitlicher Rahmen
Inhalt
Tag1
14:45 – 15:45 Uhr
Vortrag
15:45 – 15:55 Uhr
Pause
16:00 – 19:00 Uhr
Stationenlernen
19:00 – 19:10 Uhr
Ausblick
Tag2
8:45 – 9:45 Uhr
Vortrag
9:45 – 9:55 Uhr
Pause
10:00 – 11:30 Uhr
Gruppenphase
11:30 – 11:40 Uhr
Pause
11:40 – 12:25 Uhr
Präsentation
12:25 – 12:40 Uhr
Diskussion + Fragen
12:40 – 13:00Uhr
Evaluation
Tab. 5: Tagesablauf des Oberstufenkurses aus Hessen
Da sich herausstellte, dass die Stationen einen großen Konzentrationsaufwand
seitens der Schüler forderten, wurde bei der zweiten Durchführung des
Schülerlabors eine 10min Pause eingeführt. Die Versuche des Stationenlernens
konnten mit 55min Bearbeitungszeit gut durchgeführt werden. Allerdings stellte sich
heraus, dass bei erstmaligem Durchführen gegen Ende des ersten Tages die
Konzentration nachließ.
100
Zeitlicher Rahmen
Inhalt
Tag1
8:30 – 9:30 Uhr
Vortrag
9:30 – 9:40 Uhr
Pause
9:45 – 13:00 Uhr
Stationenlernen
13:00 – 13:10 Uhr
Ausblick
Tag2
11:30 – 12:45 Uhr
Vortrag
12:45 – 12:55 Uhr
Pause
13:00 – 15:00 Uhr
Gruppenphase
15:00 – 15:10 Uhr
Pause
15:15 – 16:15 Uhr
Präsentation
16:15 – 16:45 Uhr
Diskussion + Quiz
16:45 – 17:05Uhr
Evaluation
Tab. 6: Tagesablauf des Oberstufenkurses aus Rheinland – Pfalz
Dies lag daran, dass die Schüler vormittags Unterricht hatten und somit die
Beanspruchung der Konzentrationsfähigkeit an diesem Tag das normale Pensum
der Schüler weit überschritt. Ein ähnliches Bild zeigte sich bei der Durchführung des
Schülerlabors mit dem Oberstufenkurs aus Rheinland – Pfalz. Dieser hatte am
zweiten Labortag auch vormittags Unterricht, so dass die Konzentration bei den
Präsentationen sichtlich nachließ. Somit wäre für eine ausgewogene Konzentration
über die Zeitdauer des gesamten Schülerlabors der zeitliche Rahmen auf
vormittags zu begrenzen, da an den Tagen, an denen das Schülerlabor vormittags
stattfand, keine Konzentrationsprobleme auftraten. Beim erstmaligen Durchführen
des Schülerlabors wurde der Zeitaufwand des Einführungsvortrags am zweiten Tag
des Schülerlabors zu gering eingeschätzt, da es mehrere Rückfragen beim
Doppelspalt – Experiment mit einzelnen Photonen gab [Vo03]. Aus diesem Grund
wurde die Zeitdauer bei der zweiten Durchführung des Schülerlabors um 15min
ergänzt. Es zeigte sich, dass die neu angesetzte Zeitdauer des Vortrags völlig
ausreichend war, um die Inhalte präsentieren und diskutieren zu können. Da der
Oberstufenkurs aus Hessen am zweiten Tag des Schülerlabors keine Freistellung
vom Nachmittagsunterricht erhielt, musste die Gruppenphase mit eineinhalb
Zeitstunden und die Präsentation mit 45min geplant werden. Das ursprüngliche
101
Konzept
war allerdings
mit
zwei
Zeitstunden für die
Durchführung der
Gruppenphase und mit einer Stunde für die Durchführung der Präsentation geplant,
so
dass
es
hinsichtlich
des
Zeitmanagements
Probleme
gab
und
die
Diskussionsrunde leider entfallen musste. Eine zeitliche Ausdehnung war wegen
des Nachmittagunterrichts des Oberstufenkurses aus Hessen nicht möglich. Bei der
zweiten Durchführung war der zeitliche Rahmen jedoch ausreichend. Das zeitliche
Konzept in Tabelle 6 kann somit für eine nochmalige Durchführung des
Schülerlabors verwendet werden.
Die Arbeitsblätter wurden so gestaltet, dass eine selbstständige Durchführung der
Versuche möglich ist. Aus Erfahrung zeigt sich aber, dass es sinnvoll ist, jeden
Versuch mit einem Betreuer auszustatten. Die Betreuer waren in diesem
Schülerlabor ausnahmslos Lehramtsstudenten höherer Semester mit einer guten
Vorbildung in der Quantenphysik. Die Betreuer konnten so mit den Schülern
diskutieren und bei Problemen Hilfe zur Selbsthilfe geben. Es zeigte sich, dass
keine völlig selbstständige Durchführung der Versuche erfolgte. Ein Grund hierfür
war, dass die Schüler die Arbeitsblätter teilweise trotz Hinweis nicht genau genug
durchgelesen haben, wodurch sich viele Nachfragen ergaben.
Abb. 58: Schülergruppe beim Durchführen des Doppelspalt – Experiments von YOUNG
102
Die Nachfragen waren oft unnötig, da die Arbeitsblätter die Antwort auf die Fragen
explizit enthielten. Beide Oberstufenkurse verfügten über Vorkenntnisse der
Wellenoptik, wobei der Oberstufenkurs aus Rheinland – Pfalz im Gegensatz zu
dem Oberstufenkurs aus Hessen, Licht als elektromagnetische Welle und die
Polarisation von Licht im Unterricht behandelt hatte.
Das Doppelspalt – Experiment von YOUNG mit Laserlicht (Abbildung 58), die
Simulation zum Doppelspalt mit Kugeln und Elektronen (Abbildung 59) wurden
ohne weitere Probleme von allen Schülern (beide Oberstufenkurse) selbstständig
durchgeführt und ausgewertet.
Abb. 59: Schülergruppe beim Bedienen der Simulation zum Doppelspalt – Experiment
Ein Grund für den reibungslosen Ablauf bei diesem Versuch ist vermutlich die
ausführliche Behandlung des Doppelspalt – Experiments von YOUNG im Unterricht.
Das Simulationsprogramm zum Doppelspalt – Experiment wurde von allen
Schülern direkt verstanden, wodurch bei einmaliger Einweisung durch den Betreuer
keine weitere Hilfe erforderlich war. Die Konzentrationsfähigkeit der Schüler wurde
bei diesem Versuch nicht so sehr beansprucht wie bei den anderen Stationen,
wodurch diese Station als aktive Erholungsphase und ‚Auflockerung’ diente. Da die
Schüler für die Bearbeitung der Station zum Doppelspalt – Experiment weniger Zeit
im Vergleich zu den anderen Stationen benötigten, konnte ein kleiner Exkurs in die
103
Thematik der Fehlerabschätzung erfolgen. Da die Fehlerabschätzung in der Schule
im Allgemeinen keinen großen Stellenwert besitzt, konnten die Schüler auf diese
Art für die Fehlerbetrachtung sensibilisiert werden. Es stellte sich heraus, dass die
Schüler überwiegend die Messfehler als zu gering einschätzten. Die graphische
Auswertung mittels der Ausgleichgeraden bei den anderen Stationen stellte kein
Problem dar. Die Bestimmung der Steigung und des Y – Achsenabschnitts konnte
von allen Schülern problemlos erfolgen. Bei der physikalischen Interpretation
hingegen gab es große Unterschiede.
Abb. 60: Schülergruppe beim Durchführen des Versuchs zum Photoeffekt
Beim Photoeffekt (Abbildung 60) konnten fast alle Schüler des Oberstufenkurses
aus Hessen die Nullstelle als Grenzfrequenz identifizieren, aber der Y –
Achsenabschnitt konnte nur von zwei Schülern als Austrittsarbeit interpretiert
werden. Die Gleichung (2.14) konnte von keinem Schüler des Oberstufenkurses
aus Hessen aufgestellt werden.
Alle Schüler des Oberstufenkurses aus Rheinland – Pfalz konnten die Nullstelle der
Geraden als Grenzfrequenz deuten. Ein Viertel der Schüler war in der Lage, die
Austrittsarbeit mit dem Y – Achsenabschnitt in Verbindung zu bringen und die
Gleichung (2.14) ohne Hilfe aufzustellen. Allerdings konnten mit Hilfe des Betreuers
104
alle Schüler die physikalische Interpretation des Photoeffekts erarbeiten. Die
Schüler waren zum Schluss dieses Versuchs überwiegend in der Lage, den
Photoeffekt mit Hilfe der Lichtquantenhypothese (Abschnitt 2.2 und 2.3) zu
verstehen. Bei der Elektronenbeugung (Abbildung 61) hingegen konnten fast alle
Schüler beider Oberstufenkurse die physikalische Interpretation, dass Materie eine
Wellenlänge besitzt, geben, obwohl sich ungefähr die Hälfte nicht mit diesem
Gedanken anfreunden konnte. Als die Schüler das JÖNSSON – Experiment nach der
Station zur Elektronenbeugung durchführten, war die Skepsis bei einigen Schülern
nicht mehr ganz so groß.
Somit
die meisten Schüler
motiviert zum
Labortag
um mehr über die
Abb.kamen
61: Schülergruppe
beim Durchführen
deszweiten
Versuchs
zur Elektronenbeugung
Man kann durchaus behaupten, dass die Schaffung des Konflikts ‚Welle’ oder
‚Teilchen’ gelungen ist und die Schüler es nicht erwarten konnten, am nächsten Tag
mehr über die Quantenphysik zu erfahren, da die Frage nach dem ‚Warum?’ offen
blieb. Somit kamen die meisten Schüler motiviert zum zweiten Tag des
Schülerlabors um mehr über die Quantenphysik zu erfahren.
Bei der Gruppenphase zu den Interpretationen der Quantenmechanik gab es im
experimentellen Teil mit der Simulation zum Doppelspalt keine großen Probleme,
lediglich das Auflösungsvermögen einer Lichtquelle war nicht allen Schülern
bekannt. Da auch in der Gruppenphase Betreuer eingesetzt wurden, konnten diese
das Auflösungsvermögen einer Lichtquelle nochmals erklären. Die Erarbeitung der
105
Interpretationen der Quantenmechanik konnte allerdings nicht selbstständig
erfolgen. Allein aus den ausgeteilten Texten waren die Schüler nicht in der Lage,
die Kernaussagen zu verstehen. Vor allem bei der BOHMschen Interpretation der
Quantenmechanik hatten die Schüler Probleme. Die Betreuer waren sehr gefordert,
die wesentlichsten Kernaussagen der Interpretationen schülergerecht darzustellen.
Abb. 62: Schülergruppe beim Durchführen des Versuchs zum Quantenradierer
Die selbstständige Erarbeitung der Interpretationen der Quantenmechanik anhand
von Texten ist als zu schwierig einzustufen. Es bietet sich eher an, die
Interpretationen der Quantenmechanik in einem gelenkten Unterrichtsgespräch zu
erarbeiten. Das Arbeitsblatt zum MACH – ZEHNDER – Interferometer konnte beim
erstmaligen Durchführen des Schülerlabors aus Zeitgründen nicht vollständig
bearbeitet werden, wodurch das Bombentest – Experiment nicht behandelt wurde.
Beim zweiten Durchführen des Schülerlabors konnte das Arbeitsblatt zum MACH –
ZEHNDER – Interferometer vollständig bearbeitet werden. Die Auslöschung der
‚Welcher – Weg’ – Information durch den dritten Polarisationsfilter wurde ohne
Begründung erwähnt. Allerdings wollten die Schüler beider Oberstufenkurse eine
Begründung für die Auslöschung der ‚Welcher – Weg’ – Information. Der Betreuer
106
musste die nötige Erklärung (Abschnitt 4.3) geben. Ursprünglich wurde vermutet,
dass die Erklärung für die Schüler zu schwierig sei, was sich aber im Nachhinein
als falsch herausstellte. Der reale Aufbau des Quantenradierers (Abbildung 62)
wurde ausgiebig diskutiert. Es wurde auf die realen Bedingungen im Gegensatz
zum idealisierten Aufbau eingegangen und die Schüler des Oberstufenkurses aus
Rheinland – Pfalz bemerkten sogar, dass die Beobachtungen auch klassisch erklärt
werden können. Die klassische Erklärung wurde nicht erwähnt, damit die
spektakulären Beobachtungen nicht ihre Wirkung verlieren. Die Schüler hatten sehr
viel Spaß bei der Durchführung des realen Quantenradierers und so ließen sie ihrer
Kreativität freien Lauf und probierten sehr viel aus. Das Bombentest – Experiment
hatte zunächst nicht die spektakuläre Wirkung wie erwartet. Die Schüler mussten
explizit darauf aufmerksam gemacht werden, dass das Photon nur den Weg zum
Detektor mit der destruktiven Interferenz nimmt, wenn ein Hindernis einen
Strahlenweg blockiert. Weiterhin musste die Fragestellung aufgeworfen werden:
woher weiß das Photon dass ein Hindernis im anderen Strahlengang, den es nicht
genommen hat, steht? Erst dann wurde den Schülern allmählich das Prinzip der
‚wechselwirkungsfreien Messung’ bewusst und sie waren fasziniert.
Abb. 63: Schülergruppe beim Präsentieren der BOHMschen Mechanik
107
Die Präsentationen zur Komplementarität wurden mit Hilfe der entsprechenden
Simulationen gezeigt und alle weiteren notwendigen Abbildungen standen den
Schülern auf dem Computer zur Verfügung. Die Schüler setzten außerdem noch
die Tafel als Präsentationsmedium ein. Den Schülern fiel es nicht schwer das
Komplementaritätsprinzip und die Ortsdetektion der Elektronen beim Doppelspalt –
Experiment zu erklären. Des Weiteren stellte die Präsentation der Erklärung, warum
das Interferenzmuster nicht bei der Ortsdetektion durch den Zusammenstoß eines
Elektrons mit einem Photon verschwindet auch kein Problem für die Schüler dar.
Da die Komplementarität zweimal präsentiert wurde, einmal mit Hilfe des
Doppelspalt – Experiments und zum anderen mit dem MACH – ZEHNDER –
Interferometer, konnten die etwas schwächeren Schüler spätestens beim zweiten
Präsentieren die Komplementarität verstehen. Die Präsentation des Bombentest –
Experiments stellte bei der zweiten Durchführung des Schülerlabors kein Problem
dar und die Interferenzmuster des realen Quantenradierers wurden über eine
Schwanenhalskamera zur besseren Sichtbarkeit bei der Präsentation auf einen
Fernseher projiziert. Die Präsentation der Interpretationen der Quantenmechanik
(Abbildung 63) zeigte bei der ersten Durchführung des Schülerlabors, dass die
Kopenhagener Interpretation nur ansatzweise verstanden und die BOHMsche
Interpretation überhaupt nicht verstanden wurde, trotz großer Bemühungen seitens
der Betreuer, die Interpretationen zu erklären. Beim Oberstufenkurs, der beim
zweiten Schülerlabor mitwirkte, verhielt es sich allerdings anders. Die Schüler
konnten die Kopenhagener Interpretation, mit ihren eigenen Worten, so gut wie
möglich präsentieren. Die Kernaussagen der BOHMschen Interpretation wurden
allerdings nicht ganz richtig dargestellt. Aus diesem Grund kann man behaupten,
dass die BOHMsche Interpretation nur in Ansätzen verstanden wurde. In der
anschließenden Diskussionsrunde beim zweiten Schülerlabor konnte erkannt
werden, dass die Schüler eher zur BOHMschen Interpretation tendierten, weil der
Determinismus und der Bahnbegriff wieder an Bedeutung gewinnen. Als der Leiter
des
Schülerlabors
aber
verschiedene
Argumente
gegen
die
BOHMsche
Interpretation anführte, schlossen sich allerdings einige Schüler der Meinung des
Leiters an und wurden so ein wenig verunsichert. Es ist allerdings nicht tragisch,
dass die Schüler etwas verunsichert wurden, da der Leiter des Schülerlabors auch
erwähnte, dass jeder sich mit gutem Gewissen für einen Standpunkt bezüglich der
Interpretationsrichtungen entscheiden kann, ohne falsch zu liegen. Als Abschluss
108
wurde beim zweiten Schülerlabor ein Quiz (Anhang C8) durchgeführt, um die
Nachhaltigkeit zu überprüfen. Jede Quizfrage bestand aus vier vorgegeben
Antwortmöglichkeiten und wurde anonym von jedem Schüler beantwortet. Hierzu
wurden vorgefertigte Zettel (Anhang C8) mit den Antwortmöglichkeiten A, B, C und
D ausgeteilt. Die Lösungen des Quiz befinden sich ebenfalls in Anhang C8. Die
Auswertung des Quiz und die Evaluation des Schülerlabors werden im folgenden
Abschnitt dargestellt.
5.8 Evaluation und Auswertung des Schülerlabors
Um das vorliegende Konzept des Schülerlabors beurteilen zu können, wurde am
Ende des zweiten Tags des Schülerlabors eine 20 minütige schriftliche Evaluation
durchgeführt. Der Evaluationsbogen befindet sich in Anhang A. Die Auswertung
bezieht sich auf beide Schülerlabore (26 Schüler). Die Schüler sollen das
Schülerlabor hinsichtlich Informativität, Spannung, Verständlichkeit, Interesse und
Schwierigkeitsgrad bewerten. Der Evaluationsbogen lässt sich in zwei Abschnitte
unterteilen. Im ersten Abschnitt sollen die Schüler die Fragen begründet in Textform
beantworten und eventuelle Verbesserungsvorschläge machen. Im zweiten
Abschnitt werden die Schüler aufgefordert, für die vorher schriftlich beantworteten
Fragen eine Note zu vergeben.
Wie hat ihnen das Praktikum insgesamt gefallen?
Durchschnitt: 12,2
Absolute Häufigkeit
12
10
8
6
4
2
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Noten im 15 - Punkte System
Abb. 64: Gesamtbewertung des Schülerlabors
109
Es wurde als Bewertungsgrundlage das 15 – Punkte System der Oberstufe
herangezogen, um auch eine Feinabstufung bei der Notenvergabe zuzulassen. Die
Auswertungen dieser Notenvergaben sind zum Teil in diesem Kapitel abgebildet,
wobei in Anhang A Kopien der restlichen Auswertungen vorhanden sind. Außerdem
sind in diesem Kapitel die Originalaussagen der Schüler aus den Evaluationsbogen
in Anführungszeichen gesetzt. Auf der X – Achse der Histogramme sind die Noten
abgebildet und auf der Y – Achse befindet sich die Anzahl der Schüler, die die
entsprechende Note gegeben haben. In Abbildung 64 ist zu sehen, dass das
Schülerlabor mit gut bis sehr gut beurteilt wurde. Das Schülerlabor wurde als
„wesentlich interessanter und aufschlussreicher als normaler Physikunterricht“
empfunden. Darüber hinaus „hat es echt Spaß gemacht“ und es „hätte länger sein
können (4 – 5 Tage)“.
Der Stoff wurde teilweise als „sehr schwer“ empfunden, was daran liegen könnte,
dass „zu viele Themen in kurzer Zeit“ behandelt wurden und dass keine Sicherung
des neu Erlernten vollzogen wurde, da der zeitliche Rahmen fehlte. Trotzdem
wurde der Schwierigkeitsgrad (Abbildung 65) überwiegend als „genau richtig“
eingestuft. Außerdem war das „Arbeitsklima sehr angenehm“ und es konnten durch
die „individuelle Betreuung bei Fragen“ auch „Details, […] vor allem in der
Gruppenarbeit geklärt“ werden.
Das Schülerlabor wurde auch als sehr informativ bewertet (Abbildung 66). Die
Notenskala muss hierbei uminterpretiert werden, und reicht von sehr informativ (15
Punkte) bis gar nicht informativ (0 Punkte).
Schwierigkeitsgrad
18
Absolute Häufigkeit
16
14
12
10
8
6
4
2
0
viel zu leicht
eher zu leicht
genau richtig
eher zu schwer
viel zu schwer
Abb. 65: Bewertung des Schwierigkeitsgrads
110
Eine der Hauptanliegen dieses Schülerlabors ist die Begeisterung der Schüler für
die Physik. Da zwei Physik Leistungskurse anwesend waren, kann natürlich von
einem generell hohen Interesse an der Physik ausgegangen werden. Dadurch
wurde die Frage nach einer Verstärkung des Interesses an der Physik gestellt. Es
zeigte sich, dass bei der Hälfte der Schüler ein Interesse an der Physik verstärkt
werden konnte, neun Schüler sowieso ein hohes Interesse besaßen, wodurch
dieses Schülerlabor bei ihnen keine Verstärkung hervorrief, und bei vier Schülern
das Interesse der Physik überhaupt nicht vorhanden war.
Wie informativ fanden Sie das Praktikum?
Durchschnitt: 12,7
Absolute Häufigkeit
10
8
6
4
2
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
Noten im 15 - Punkte System
Abb. 66: Bewertung der Informativität des Schülerlabors
Um herauszufinden, ob das generelle Interesse an der Physik durch dieses
Schülerlabor geweckt werden konnte, wurde noch eine quantitative Erhebung mit
Hilfe des Notensystems (Abbildung 67) unternommen. Auch in diesem Fall muss
die Notenskala wieder uminterpretiert werden, und zwar von Interesse auf jeden
Fall geweckt (15 Punkte) bis Interesse gar nicht geweckt (0 Punkte). Es ist in
Abbildung 67 zu erkennen, dass bei einem Drittel der Schüler das Interesse an der
Physik auf jeden Fall geweckt wurde und bei der Hälfte der Schüler das Interesse
an der Physik etwas geweckt wurde.
111
Hat dieses Praktikum ihr Interesse an der Physik geweckt?
Durchschnitt: 10,8
Absolute Häufigkeit
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
2
1
0
Noten im 15 - Punkte System
Abb. 67: Bewertung des Interesses an der Physik
Absolute Häufigkeit
Wie hat ihnen die Thematik "Interpretationen der
Quantenmechanik" gefallen
Durchschnitt: 11,4
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
Noten im 15 - Punkte System
Abb. 68: Bewertung der Thematik: ‚Interpretationen der Quantenmechanik’
Obwohl die „Komplexität […] ein bisschen abgeschreckt“ hat, hat das Schülerlabor
„auf jeden Fall mein Interesse verstärkt, weil ich Vorurteile (Quantenphysik ist
langweilig …) hatte, aber positiv überrascht war, wie mysteriös das Ganze ist.“.
Trotz des großen stofflichen Umfangs konnten die meisten Schüler über die
spannenden und interessanten Themen motiviert werden, so dass man feststellen
konnte, dass schwierige Themen nur interessant sein müssen, um die Schüler zu
begeistern. Die Schwierigkeit der Themen ist für die Schüler nur sekundär, was die
Thematik der ‚Interpretationen der Quantenmechanik’ zeigt (Abbildung 68). Die
Schüler empfanden die Interpretationen der Quantenmechanik als schwierig, aber
112
trotzdem hat ihnen die Thematik gefallen und das Interesse an der Physik verstärkt,
weil „ich nun gemerkt habe, dass bei weitem noch nicht alles erforscht ist“. Dies ist
im Wesentlichen die Aussage vieler Schüler, was zeigt, dass die Schüler ein
vollständiges Bild der Physik im Kopf haben, und denken, dass es in der Physik
keine offenen Fragen mehr gibt. Somit wurde den Schülern ein neues – nicht
deterministisches – physikalisches Weltbild vermittelt, das Weltbild der Physiker
des 20. Jahrhunderts und die Schüler hatten zum ersten Mal die Möglichkeit über
das physikalische Weltbild des 19. Jahrhunderts (Lokalität und Determinismus)
hinauszukommen.
Aus
diesen
Gründen
können
die
Interpretationen
der
Quantenmechanik in solch einem Schülerlabor nicht weggelassen werden, lediglich
eine andere Vermittlung (z.B. gelenktes Unterrichtsgespräch), als in diesem
Schülerlabor, ist anzustreben. Das selbständige Durchführen und Auswerten der
Versuche wurde sowohl als besonders „spannend und interessant“ bewertet, als
auch „zusätzlich motivierend“. Die Arbeitsblätter und die Handouts wurden ohne
große Verbesserungsvorschläge als gut bis sehr gut eingeschätzt (Anhang A),
wobei die Texte zu den Interpretationen der Quantenmechanik teilweise als zu lang
und schwierig bewertet wurden, aber dennoch immer die interessante Darstellung
der Thematik erwähnt wurde. Ansonsten waren die Arbeitsblätter und die Handouts
verständlich
(Auswertung
siehe
Anhang
A)
und
ermöglichten
mit
ihren
Informationen die Versuche durchzuführen. Das Doppelspalt – Experiment mit Licht
wurde als langweilig erachtet, da es schon im Unterricht ausgiebig behandelt
wurde. Es zeigt sich dadurch, dass die Schüler in einem Schülerlabor neue
physikalische Themen verlangen, die nicht vom Unterricht her bekannt sind. Auch
der erste Teil des Vortrags am ersten Tag wurde als langweilig eingestuft, da viel
Bekanntes aus dem Unterricht wiederholt wurde. Es ist allerdings beim Thema
Quantenphysik sehr schwer, in einem zweitägigen Schülerlabor dem Wunsch nach
neuem Wissen und adäquater Vermittlung nachzukommen, da die Informationsflut
sehr schnell ansteigt. Der zweite Vortrag wurde vor allem wegen der hohen
Informationsflut und langen Zeitdauer kritisiert, obwohl alle physikalischen Inhalte
des Vortrags wichtig waren und somit nicht weggelassen werden können. Es bietet
sich allerdings auf Wunsch der Schüler eine kleine Pause an, die den Schülern hilft,
ihre Konzentrationsfähigkeit wieder zu erlangen. Des Weiteren wurde von den
Schülern noch mehr Interaktion in den Vorträgen gefordert, wodurch die Zeitdauer
der Vorträge natürlich wieder erhöht wird. Trotz dieser Kritik wurden die Vorträge
113
von zwei Drittel der Schüler als verständlich und anschaulich empfunden. Die
„eingesetzten Medien haben das Programm abgerundet und den Inhalt visualisiert“.
Die Simulationen wurden positiv bewertet, wobei „Realexperimente [doch]
spannender sind“. Die Mischung aus Realexperimenten und Simulationen kam sehr
gut bei den Schülern an.
Es war auch ein Leistungsgefälle der Oberstufenkurse aus Hessen und Rheinland –
Pfalz festzustellen. Der Oberstufenkurs aus Rheinland – Pfalz hatte eine wesentlich
schnellere Auffassungsgabe als der Oberstufenkurs aus Hessen. Dies könnte zwei
Gründe haben, zum einen hat der Oberstufenkurs aus Hessen eine geringere
Vorbildung bezüglich der Wellenoptik und der Eigenschaften von Licht und zum
anderen war der Oberstufenkurs aus Rheinland – Pfalz aus zwei Leistungskursen
der selben Schule zusammengesetzt. Die Schüler hatten sich freiwillig gemeldet um
an diesem Schülerlabor teilzunehmen. Nach Rücksprache mit dem verantwortlichen
Lehrer
des
Oberstufenkurses
aus
Rheinland
–
Pfalz
sollte
aber
keine
Überbewertung der freiwilligen Teilnahme erfolgen, da es noch mehr Schüler in den
beiden Leistungskursen gab, die gerne an dem Schülerlabor teilnehmen wollten,
aber aus Platzgründen in der Schule bleiben mussten.
Das Quiz in Anhang C8 zeigte auch, dass die wesentlichen Inhalte, die es zu
vermitteln gab, verstanden wurden. Alle Fragen bis auf die Fragen drei, vier und
fünf wurden komplett richtig beantwortet. Frage drei beantworteten zwei, Frage vier
ein und Frage fünf drei Schüler falsch. Allerdings darf dies natürlich nicht
überbewertet werden, da das Quiz unmittelbar nach dem Schülerlabor stattfand.
Ein weiterer Wissenstest im Abstand von 4 – 6 Wochen war leider nicht, bedingt
durch die Sommerferien, möglich.
Interessant ist auch die Frage: Kann der Unterricht von diesem Schülerlabor
profitieren? Die Lehrer der Oberstufenkurse wurden gebeten, zu dieser Frage
Stellung zu nehmen.
Durch die „methodische Aufbereitung von unterrichtsrelevantem Stoff“ [Lehrer aus
Rheinland – Pfalz] kann der physikalische Inhalt des Schülerlabors im Unterricht
verwendet werden. Auch „die erstellten Arbeitsmaterialien sind prinzipiell für den
Unterricht geeignet“, so der Lehrer aus Rheinland – Pfalz. Das Stationenlernen am
ersten Tag des Schülerlabors könnte sogar, nach der Meinung des Lehrers aus
Rheinland – Pfalz, im Unterricht umgesetzt werden, da das verwendete Equipment
für diese Experimente fast an jeder Schule vorhanden ist. Die Elektronenbeugung
114
und der Photoeffekt sind insbesondere für die Unterrichtseinheiten beider Lehrer
von großer Bedeutung, da beide Experimente zentrale Unterrichtselemente der
Quantenphysik sind. Beide Lehrer sind auch der Meinung, dass die Schüler sehr
stark von dem Schülerlabor profitieren, da z.B. das MACH – ZEHNDER –
Interferometer, im Gegensatz zum Doppelspalt – Experiment, im Unterrichtskonzept
beider Lehrer nicht angesprochen wird. Genauso verhält es sich auch mit den
Interpretationen der Quantenmechanik. Abschließend ist noch zu sagen, dass
beide Lehrer leider keine direkte Zeitersparnis durch das Schülerlabor für den
Themenblock der Quantenphysik haben, da nichts weggelassen werden kann,
dafür „investiert man genauso viel Zeit, erreicht aber eine bessere Verständnistiefe“
[Lehrer aus Hessen].
115
6. Zusammenfassung
In der vorliegenden Examensarbeit wurde aufgezeigt wie ein zweitägiges
Schülerlabor die Charakteristika (Abschnitt 5.4) der Quantenphysik vermitteln
konnte. Durch die eingesetzte Arbeitsform der Gruppenarbeit konnte ein
selbständiges und schülerorientiertes Arbeiten erreicht werden, welches zur
Motivation und regen Teilnahme animierte. Am ersten Tag des Schülerlabors
wurden die Schüler durch ein Stationenlernen zum Welle – Teilchen – Dualismus
zum Nachdenken angeregt, wodurch die Motivation der Schüler am zweiten Tag
des Schülerlabors aufrechterhalten werden konnte. Am zweiten Tag des
Schülerlabors wurde das Komplementaritätsprinzip der Quantenphysik erarbeitet
und
die
Schüler
erhielten
Interpretationsrichtungen
durch
die
der Quantenphysik
Auseinandersetzung
einen Einblick
in
mit
den
ein neues,
nichtdeterministisches und nichtlokales Weltbild der Physik. Es konnte den
Schülern gezeigt werden, dass es in der Physik immer noch offene Fragen und
ungelöste Probleme gibt. Durch die Aktualität der Diskussionen um die
Interpretationen der Quantenphysik konnte das Interesse der Schüler an der Physik
deutlich verstärkt werden (Abschnitt 5.8).
Ein wichtiger Baustein des Schülerlabors war neben dem Doppelspalt – Experiment
eine didaktische Alternative: das MACH – ZEHNDER – Interferometer. Dieses wurde
als Quantenradierer in einem Realexperiment aufgebaut und bot somit die
Möglichkeit die Komplementarität nicht nur anhand von Simulationen zu
beobachten. Die wichtigsten Charakteristika der Quantenphysik (Abschnitt 5.4),
konnten somit in diesem Schülerlabor an Realexperimenten erarbeitet werden,
wodurch die Authentizität der Physik gewahrt wird. Der Quantenradierer kann mit
geringem Aufwand und geringen Kosten nachgebaut werden, wodurch den Schulen
der Aufbau eines modernen und aktuellen Demonstrationsexperiments zur
Quantenphysik ermöglicht wird.
Eine Erweiterung des aufgebauten Quantenradierers ist auch möglich, so dass
ähnlich wie in dem Doppelspalt – Experiment mit einzelnen Photonen [Vo03], das
allmähliche Aufbauen des Interferenzmusters (Abbildung 27) beobachtet werden
kann. Mit diesem Aufbau können in einem Realexperiment das Messproblem und
116
die damit zusammenhängenden Interpretationen der Quantenmechanik vertieft
werden.
Einer möglichen thematischen Erweiterung des Schülerlabors sind auch keine
Grenzen
gesetzt,
denn
in
weiteren
Tagen
könnte
man
z.B.
die
Quantenkryptographie, die Quantenteleportation und das damit zusammenhängende EPR – Paradoxon behandeln [Zei05]. In diesem Zusammenhang kann
dann auch stärker auf das Messproblem in der Quantenmechanik eingegangen
werden und die Interpretationen der Quantenmechanik, vor allem die Nichtlokalität
eventuell besser verstanden werden. Im Gegensatz zu den thematischen Inhalten –
die schon schwierig und komplex genug waren – des im Rahmen dieser
Staatsexamensarbeit
Erweiterungen
durchgeführten
(Quantenkryptographie,
Schülerlabors
sind
die
Quantenteleportation
thematischen
und
EPR
–
Paradoxon) zwar weit weg vom Lehrplan, aber durchaus sehr interessant für
Schüler.
117
7. Anhang
Anhang A: Evaluationsbogen und Auswertung der
Evaluation
Evaluationsbogen
Schülerlabore an Universitäten zum Thema Quantenphysik werden nicht oft
angeboten, weil das Themengebiet der Quantenphysik als sehr schwierig eingestuft
wird. Um einen Eindruck davon zu bekommen, wie Ihnen die Praktikumstage
gefallen haben, möchten wir Sie bitten einige Fragen zu beantworten und
Verbesserungsvorschläge zu machen. Die Fragebögen sind natürlich anonym.
Wie
hat
Ihnen
das
Verbesserungsvorschläge?
Praktikum
insgesamt
gefallen?
Haben
Sie
Hat das Praktikum Ihr Interesse an der Physik verstärkt? Begründung!
Fanden Sie das Praktikum interessant? Was fanden Sie besonders spannend und
was nicht? Haben Sie Verbesserungsvorschläge?
Der Schwierigkeitsgrad des Praktikums war
c
c
c
c
c
viel zu leicht
eher zu leicht
genau richtig
eher zu schwer
viel zu schwer
118
Wie bewerten Sie die Vorträge im Hinblick auf Verständlichkeit und Schwierigkeit?
Haben Sie Verbesserungsvorschläge?
Wie fanden Sie die Handouts? Waren die Handouts hilfreich oder könnte man die
Versuche
auch
ohne
Handouts
durchführen?
Haben
Sie
Verbesserungsvorschläge?
Erster Praktikumstag
War die mathematische Schulbildung ausreichend um die Auswertung der
Versuche zu machen.
Hat die Zeit ausgereicht um die Versuche durchzuführen und die Auswertung zu
machen? Haben Sie Verbesserungsvorschläge?
Station 1: Äußerer lichtelektrischer Effekt (Hallwachseffekt/Photoeffekt)
War das Arbeitsblatt verständlich? Haben Sie Verbesserungsvorschläge?
119
War der Versuch durch das Arbeitsblatt ausreichend erklärt oder hätten Sie mehr
Information benötigt?
Station 2: Elektronenbeugung (DEBYE – SCHERRER – Verfahren)
War das Arbeitsblatt verständlich? Haben Sie Verbesserungsvorschläge?
War der Versuch durch das Arbeitsblatt ausreichend erklärt oder hätten Sie mehr
Information benötigt?
Station 3: Doppelspalt – Experiment (YOUNG – Experiment /JÖNSSON –
Experiment)
War das Arbeitsblatt verständlich? Haben Sie Verbesserungsvorschläge?
120
War der Versuch durch das Arbeitsblatt ausreichend erklärt oder hätten Sie mehr
Information benötigt?
Zweiter Praktikumstag
War die Zeit ausreichend um die Arbeitsblätter und die Präsentation zu machen?
Welchen Gruppenversuch haben Sie durchgeführt?
( ) MACH – ZEHNDER – Interferometer
( ) Kopenhagener Interpretation der Quantenmechanik
( ) BOHMsche Interpretation der Quantenmechanik
War das Arbeitsblatt verständlich? Haben Sie Verbesserungsvorschläge?
Waren die Versuche durch das Arbeitsblatt ausreichend erklärt oder hätten Sie
mehr Information benötigt?
121
Wie fanden Sie das Experimentieren mit Hilfe der Simulationen?
Nur für die Gruppen, die die Interpretationen der Quantenmechanik hatten:
War der ausgeteilte Text verständlich?
Vergeben Sie nun für die folgende Teile Schulnoten im 15 – Punkte System!
Fragen
Wie hat Ihnen das Praktikum
insgesamt gefallen?
Wie hat Ihnen der erste
Praktikumstag gefallen?
Wie hat Ihnen der zweite
Praktikumstag gefallen?
Wie informativ fanden Sie das
Praktikum?
Wie hat ihnen der Vortrag am ersten
Tag gefallen?
Wie hat ihnen der Vortrag am
zweiten Tag gefallen?
Wie fanden Sie das Handout des
ersten Tags?
Wie fanden Sie das Handout des
zweiten Tags?
Wie fanden Sie das Arbeitsblatt zum
Hallwachseffekt?
Wie fanden Sie das Arbeitsblatt zur
Elektronenbeugung?
Wie fanden Sie das Arbeitsblatt zum
Doppelspaltexperiment?
Wie bewerten Sie das Arbeitsblatt in
der Gruppenphase?
Hat ihnen die Thematik
„Interpretation der
Quantenmechanik“ gefallen?
Hat dieses Praktikum ihr Interesse
an der Physik geweckt?
Note
122
Absolute Häufigkeit
Wie hat ihnen der erste Praktikumstag gefallen ?
Durchschnitt: 11,7
9
8
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
2
1
0
2
1
0
Noten im 15 - Punkte System
Absolute Häufigkeit
Wie hat ihnen der zweite Praktikumstag gefallen?
Durchschnitt: 12
8
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
Noten im 15 - Punkte System
Wie hat ihnen der Vortrag am ersten Tag gefallen?
Durchschnitt: 11,5
Absolute Häufigkeit
10
8
6
4
2
0
15
14
13
12
11
10
9
8
7
6
5
4
3
Noten im 15 - Punkte System
123
Wie hat ihnen der Vortrag am zweiten Tag gefallen?
Durchschnitt: 11,2
Absolute Häufigkeit
10
8
6
4
2
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
2
1
0
2
1
0
Noten im 15 - Punkte System
Absolute Häufigkeit
Wie fanden Sie das Handout des ersten Tags?
Durchschnitt: 12,6
8
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
Noten im 15 - Punkte System
Absolute Häufigkeit
Wie fanden Sie das Handout des zweiten Tags?
Durchschnitt: 12,7
8
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
Noten im 15 - Punkte System
124
Absolute Häufigkeit
Wie fanden Sie das Arbeitsblatt zum Hallwachseffekt?
Durchschnitt: 12
8
7
6
5
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
0
1
0
Noten im 15 - Punkte System
Wie fanden Sie das Arbeitsblatt zur Elektronenbeugung?
Durchschnitt: 11,9
Absolute Häufigkeit
10
8
6
4
2
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
Noten im 15 - Punkte System
Wie fanden Sie das Arbeitsblatt zum Dopplspalt - Experiment?
Durchschnitt: 11,8
Absolute Häufigkeit
10
8
6
4
2
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
Noten im 15 - Punkte System
125
Wie fanden Sie das Arbeitsblatt zum Mach - Zehnder Interferometer? Durchschnitt: 11,9
Absolute Häufigkeit
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
2
1
0
1
0
Noten im 15 - Punkte System
Wie fanden Sie das Arbeitsblatt zur Kopenhagener
Interpretation? Durchschnitt: 12,8
Absolute Häufigkeit
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
Noten im 15 - Punkte System
Wie fanden Sie das Arbeitsblatt zur Bohmschen Interpretation?
Durchschnitt: 10,6
Absolute Häufigkeit
4
3
2
1
0
15
14
13
12
11
10
9
8
7
6
5
4
3
2
Noten im 15 - Punkte System
126
Anhang B: Bauteile des Quantenradierers mit
Preisinformation
€ 115,00
1
€ 115,00
G050309000 Reduzierfassung 16/25
€ 12,00
1
€ 12,00
G061010000 Aufnahmeplatten 25/30/35
€ 20,00
4
€ 60,00
G061020000 Aufnahmeplatte 25/30/35, einklinkbar
€ 29,00
8
€ 58,00
G061023000 Aufnahmeplatte 25/30/35, einklinkbar
€ 32,00
6
€ 96,00
G061025000 Zentrieraufnahmeplatte/-halter 25
€ 90,00
2
€ 90,00
G061041000 Aufnahmeplatte 25 mit Befestigungsbohrungen
€ 32,00
3
€ 32,00
G061070000 Aufnahmeplatte 25 - T 10
€ 35,00
4
€ 35,00
€ 115,00
1
€ 460,00
G061210000 Stangen
€ 10,00
2
€ 80,00
G061228000 Stangenhalter G/F/90°
€ 22,00
2
€ 132,00
G061654000 Irisblenden Mikrobank
€ 79,00
2
€ 158,00
€ 125,00
3
€ 375,00
G065092000 Stellring 30
€ 19,00
4
€ 76,00
G311027000 Bikonvexlinsen aus Quarzglas
€ 79,00
1
€ 79,00
G340060000 Planspiegel mit Aluminiumbeschichtung - eckige Form € 30,00
2
€ 60,00
G344143000 Strahlteilerplatten 20x30 mm
2
€ 64,00
G040902000 Diodenlaser x.ldm 405 bis 830 nm
G061084000 Umlenkwürfel
G063406000 Polarisationsfilter Typ VIS 4 K
€ 32,00
Gesamtpreis LINOS PHOTONICS (Netto): 1982€
Gesamtpreis LINOS PHOTONICS (Brutto): 2358,58€
Gesamtpreis (Netto) mit Montageplatte und Blendenhalterungen: ca. 2650€
127
Anhang C: Verwendete Materialien auf beiliegender
CD
-
C1: Arbeitsblätter des Stationenlernens
C2: Arbeitsblätter der Gruppenphase
C3: Vortrag des ersten Tags
C4: Vortrag des zweiten Tags
C5: Handout des Vortrags am ersten Tag
C6: Handout des Vortrags am zweiten Tag
C7: Poster des Institutstreffs
C8: Quantenquiz
C9: Quellen der im Anhang verwendeten
Abbildungen
128
8. Referenzen
8.1 Literatur
[BdW04]
Bild der Wissenschaft: Ausgabe 08/2004, Leinfelden – Echterdingen:
Konradien Medien GmbH 2004.
[Boh85]
Bohr, N. Erkenntnistheoretische Fragen in der Physik und die
menschlichen Kulturen, Ansprache beim internationalen Kongress für
Anthropologie und Ethnologie 1938, Nature 143, 268, 1939;
abgedruckt in: Atomphysik und menschliche Erkenntnis – Aufsätze
und Vorträge aus den Jahren 1930 bis 1961, Braunschweig: Vieweg
1985.
[Bom52]
Bohm, D.: A suggested interpretation of the quantum theory in terms
of „hidden“ variables. In Phys. Rev. 85, S. 166 – 179, 1952.
[Dem05]
Demtröder,
W.:
Experimentalphysik
3.
3.
überarb.
Auflage,
Berlin/Heidelberg/New York: Springer – Verlag 2005.
[Dem99]
Demtröder, W.: Experimentalphysik 2. Berlin/Heidelberg/New York:
Springer – Verlag 1999.
[Eu05]
Euler, M.: Informelles Lernen im Schülerlabor. Naturwissenschaften im
Unterricht – Physik, 16 (Nr.90) S. 4 – 12. Kiel: IPN 2005. Siehe auch:
www.lernort-labor.de/download/niuThemen heft_Basisartikel_Euler.pdf
(03.08.07).
[Fag05]
Fagundes, M. B.: Dissertation: Der Epistemologische Vektor am
Beispiel der Lichtausbreitung im Mach – Zehnder – Interferometer.
Berlin
2005.
Siehe
auch:
http://www.diss.fu-berlin.de/2005/327/
(22.08.07).
129
[Fey71]
Feynman,
R.
P.:
Vorlesungen
über
Physik:
Band
3,
Quantenmechanik. München: Oldenbourg 1971.
[Fil04]
Filk, T.: Skript zur Vorlesung: Grundlagen und Probleme der
Quantenmechanik. Universität Freiburg: Wintersemester 2004/2005.
[Ge99]
Gerthsen, C.: Physik. 20. aktualisierte Auflage, Hrsg. Helmut Vogel.
Berlin/Heidelberg/New York: Springer – Verlag 1999.
[Gre98]
Grehn, J., Krause J.: Metzler Physik. 3. Auflage. Hannover: Schroedel
Verlag 1998.
[Gri06]
Gribbin, J.: Auf der Suche nach Schrödingers Katze. 3. Auflage,
Taschenbuchausgabe. München: Piper Verlag 2006.
[Gug06]
Guggenbühl, S.: Skript zur Quantenphysik. Aarau: 2006. Siehe auch:
http://www.nksa.ch/kontakte/fachschaften/physik/mat/qm/qmgug2.pdf
(16.07.07).
[Heu06]
Heuser, H.: Funktionalanalysis. 4. durchges. Auflage. Wiesbaden:
Teubner 2006.
[Hop67]
Hoppe, E.: Geschichte der Optik. Wiesbaden: Dr. Martin Sändig oHG.
1967.
[Hu64]
Huygens, C.: Abhandlung über das Licht. Hrsg.: E. Lommel.
Darmstadt: Wissenschaftliche Buchgesellschaft 1964.
[Hun84]
Hund, F.: Geschichte der Quantentheorie. 3. überarb. Auflage,
Mannheim/Wien/Zürich: Bibliographisches Institut 1984.
[Kip90]
Kipnis,
N.:
History
of
the
principle
of
interferenc
of
light.
Basel/Boston/Berlin: Birkhäuser 1990.
130
[Küb02]
Küblbeck J., Müller, R.: Die Wesenszüge der Quantenphysik. Köln:
Aulis Verlag Deubner 2002.
[Küb04]
Küblbeck J.: Führungswellen – eine Interpretation mit verborgenen
Parametern. Praxis der Naturwissenschaften – Physik Heft 1/53. Köln:
Aulis Verlag Deubner 2004.
[Le02]
Leisen, J.: Quantenphysik/Mikroobjekte. Handreichung zum neuen
Lehrplan Physik in der Sekundarstufe II. Hrsg.: Pädagogisches
Zentrum Rheinland – Pfalz, Bad Kreuznach 2002.
[Ley07]
http://www.leybold-didactic.de/literatur/hb/d/p5/p5351_d.pdf
(31.07.07).
[Li07]
http://www.linos.com/pages/no_cache/home/welcome/ (31.07.07).
[Lpr07]
Lehrplan Rheinland – Pfalz für die Jahrgangstufen 11 bis 13 für das
Grund – und Leistungsfach Physik der gymnasialen Oberstufe 2007.
Siehe auch: http://www.uni-koblenz.de/~odsleis/lehrplan-physik/
lehrplan.pdf (03.08.07).
[Moh00]
Mohr, F.: Experimentieranleitung zum Zweistrahl – Interferometer.
Göttingen:
Linos
Photonics
GmbH
2000.
Siehe
http://www.linos.com/pages/mediabase/original/zweistrahlinterferomet
er_4254.pdf (31.07.07).
[Mül99]
Müller R., Hartmann S.: Kopenhagen contra Bohm. Praxis der
Naturwissenschaften – Physik Heft 4/48. Köln: Aulis Verlag Deubner
1999.
[Mül00]
Müller R., Wiesner H.: Das Münchner Unterrichtskonzept zur
Quantenmechanik. Physik in der Schule 38 2000. Überarbeitete
Fassung
von
Bernadette
Schorn
unter
www.cip.physik.uni-
muenchen.de/~milq/kap1/images/Lehrtext%20milq.pdf (18.07.07).
131
[Mül05]
Müller R.: Qualitative Quantenphysik: Eine Handreichung für die
Sekundarstufe 1. Hrsg.: Physik im Kontext. Kiel 2005.
Siehe
auch:
http://www.uni-kiel.de/piko/einheiten/quantenphysik/
downloads/Quantenphysik_RMüller_mitTitel_050322.pdf (31.07.07)
[Mz07]
www.student.uni-oldenburg.de/frauke.soehle/Quantenphysik/MachZehnder.ppt (24.07.07).
[Ne52]
Newton, I.: Opticks. New York: Dover Publications 1952.
[Old03]
Ludger, H.: Projektbericht Oberstufenworkshop Quantenmechanik.
Carl von Ossietzky Universität Oldenburg 2003.
[Osp07]
http://www.oberstufenphysik.de/quanten/btestpr.html (20.08.07).
[Ott03]
Otten,
E.:
Repititorium
der
Experimentalphysik.
2.
Auflage,
Berlin/Heidelberg/New York: Springer – Verlag 2003.
[Pas07]
PASCO scientific: 10101 Foothills Blvd.; Roseville, California; 95747 –
7100 USA. Siehe auch: http://www.pasco.com (20.08.07).
[Ph02]
http://physicsweb.org/articles/world/15/9/2 (07.06.07).
[Phy07]
http://shop.phywe.de/index.php?mid=360&lng=de&prod=448981&prse
a=Quantenradierer (31.07.07).
[Pi72]
Piaget J.: Theorien und Methoden der Modernen Erziehung. Wien:
Molden 1972.
[Si90]
Simonyi, K.: Kulturgeschichte der Physik. Frankfurt am Main: Verlag
Harri Deutsch 1990.
[Tip00]
Tipler, P. A.: Physik. Heidelberg/Berlin/Oxford: Spektrum Akad. Verlag
2000.
132
[Tip03]
Tipler P. A., Llewellyn R. A.: Moderne Physik. München/Wien:
Oldenbourg Wissenschaftsverlag 2003.
[Vo03]
Vogl,
C.:
Schulexperimente
(Staatsexamensarbeit).
zum
Universität
Dualismus
Mainz:
2003.
des
Lichts
Siehe
auch:
http://www.physik.uni-mainz.de/lehramt/dualismus/texte/
Staatsexamensarbeit.pdf (23.07.07).
[Wi07]
http://de.wikipedia.org/wiki/Bohmsche_Mechanik (28.04.07).
[Wie00]
Wiesner H., Müller R.: Das Münchner Unterrichtskonzept zur
Quantenmechanik. Physik in der Schule S. 126: 2000. Siehe auch:
http://www.tu-braunschweig.de/Medien-DB/ifdn/munterrichtskonzept.pdf (03.08.07).
[Zei05]
Zeilinger, A.: Einsteins Schleier. München: Goldmann Verlag 2005.
[Zei07]
Zeilinger, A.: Einsteins Spuk. München: Goldmann Verlag 2007.
8.2 Simulationen
[Mz99]
http://www.didaktik.physik.uni-muenchen.de/materialien/
inhalt_materialien/interferometer/index.html (29.07.07).
[Do99]
http://www.didaktik.physik.uni-muenchen.de/materialien/
inhalt_materialien/doppelspalt/index.html (29.07.07).
[Wwm98]
http://homepage.univie.ac.at/franz.embacher/Quantentheorie/Bombe/
(29.07.07).
133
8.3 Abbildungen
Abb. 1: [Kip90, S. 55]
Abb. 2: www.ntt.co.jp/news/news05e/0506/gif/050614_1.gif (04.07.07)
Abb. 3: [Ge99, S. 517]
Abb. 4: [Dem99, S. 188]
Abb. 5: http://pages.usherbrooke.ca/bcm-514-bl/Polarisation.gif (10.07.07)
Abb. 6: [Tip94, S. 1045]
Abb. 7: http://www.peter-junglas.de/fh/vorlesungen/physik4/html/kap2-2.html
(12.07.07)
Abb. 8: [SI90, S. 393]
Abb. 9: [Tip00, S. 1197]
Abb. 10: [Tip00, S. 1197]
Abb. 11: [Tip03, S. 154]
Abb. 12: [Tip00, S. 1213]
Abb. 13: [Tip00, S. 1213]
Abb. 14: [Si90, S. 447]
Abb. 16: [Dem05, S. 86]
Abb. 17: [Fey71, S. 1 – 3]
Abb. 18: [Fey71, S. 1 – 6]
Abb. 19: [Fey71, S. 1 – 9]
Abb. 20: [Mz07]
Abb. 21: [Fil04, S. 89]
Abb. 22: [Mül99, S. 15]
Abb. 23: [Mz07]
Abb. 24: [Li00, S. 6]
Abb. 25: [Li00, S. 7]
Abb. 26: Screenshot aus der Simulation [Mz99]
Abb. 27: [Mül00, S. 27]
Abb. 29: http://www.linos.com/pages/no_cache/home/shop- mechanik/
aufbaumaterial/stativmaterial/montageplatten/?sid=12568&cHash=
38456c82e3#sid12568 (30.07.07)
134
Abb. 30: http://www.linos.com/pages/no_cache/home/shop-mechanik/banksysteme/
mikrobank/aufbauen/halter/?sid=12801&cHash=
4f7254c6e5#sid12801 (30.07.07)
Abb. 31: http://www.linos.com/pages/no_cache/home/shop-mechanik/banksysteme/
mikrobank/aufbauen/wuerfel/?sid=13082&cHash=
62980fce82#sid13082 (30.07.07)
Abb. 32: http://www.linos.com/pages/no_cache/home/shop-optik/planoptik
/spiegel/planspiegel/?sid=12690&cHash=
6a61bb5a82#sid12690 (30.07.07)
Abb. 33: http://www.linos.com/pages/no_cache/home/shop-optik/planoptik
/strahlteiler/?sid=12619&cHash=
eb71a02d29#sid12619 (30.07.07)
Abb. 34: http://www.linos.com/pages/no_cache/home/shop-mechanik/instrumente/
laser/diodenlaser/?sid=13363&cHash=
b7405521b8#sid13363 (30.07.07)
Abb. 35: http://www.linos.com/pages/no_cache/home/shop-mechanik/banksysteme
/mikrobank/justieren/positionierer/?sid=12803&cHash=
77270566da#sid12803 (30.07.07)
Abb. 36: http://www.linos.com/pages/no_cache/home/shop-mechanik/banksysteme/
mikrobank/aufbauen/aufnahmeplatten/?sid=13063&cHash=
e70a74d959#sid13063 (30.07.07)
Abb. 44: http://www.physik.tu-berlin.de/institute/IFFP/moses/Subsites/themenseiten/
photoeffekt/photoeffektindex.html (02.08.07)
Abb. 46: www.delphi.uni-wuppertal.de/~kind/ap3ch.pdf (02.08.07)
Abb. 47: Origin 7.5
Abb. 51: http://www.cip.physik.uni-muenchen.de/~milq/kap5/images/kap5.pdf
(02.08.07)
Abb. 52: http://www.cip.physik.uni-muenchen.de/~milq/kap5/images/kap5.pdf
(02.08.07)
Abb. 53: Origin 7.5 Pro
Abb. 54: Origin 7.5 Pro
Abb. 55: [Do99]
Abb. 56: [Mz99]
Abb. 57: [Wwm98]
135
8.4 Portraits
Alle Portraits in Kapitel 2 entstammen der Webseite:
http://www-groups.dcs.st-and.ac.uk/~history/ (01.08.07),
außer das Portrait von Heinrich Hertz:
http://physics.rug.ac.be/Fysica/Geschiedenis/Mathematicians/hertz.html (01.08.07)
136
Abbildungsverzeichnis
Abbildung 1:
Interferenz zweier Wasserwellen......................................................................
5
Abbildung 2:
Interferenzmuster am Doppelspalt....................................................................
5
Abbildung 3:
Gangunterschiede.............................................................................................
6
Abbildung 4:
Polarisation des Lichts......................................................................................
7
Abbildung 5:
Polarisationsfilter...............................................................................................
8
Abbildung 6:
Polarisator und Analysator................................................................................
9
Abbildung 7:
Elektromagnetische Welle................................................................................
11
Abbildung 8:
Offene Probleme...............................................................................................
13
Abbildung 9:
Spektralverteilung eines schwarzen Körpers....................................................
14
Abbildung 10:
Experimentelle Realisierung eines schwarzen Körpers....................................
14
Abbildung 11:
Spektrale Verteilung der Hohlraumstrahlung bei 1600 K..................................
15
Abbildung 12:
Versuchsaufbau des DAVISSON – GERMER – Experiments................................
19
Abbildung 13:
Winkelabhängigkeit der Intensität der gestreuten Elektronen...........................
20
Abbildung 14:
Analogie zwischen klassischer Mechanik und Strahlenoptik............................
21
Abbildung 15:
Versuchsaufbau zum Doppelspalt – Experiment..............................................
28
Abbildung 16:
Allmählicher Aufbau des Interferenzmusters aus einzelnen Treffern...............
29
Abbildung 17:
Doppelspalt – Experiment mit Kugeln...............................................................
30
Abbildung 18:
Doppelspalt – Experiment mit Elektronen.........................................................
31
Abbildung 19:
Ortsmessung am Doppelspalt...........................................................................
34
Abbildung 20:
Das MACH – ZEHNDER – Interferometer.............................................................
36
Abbildung 21:
Das Bombentest – Experiment.........................................................................
41
Abbildung 22:
Bahnen der Elektronen im Doppelspaltversuch................................................
47
Abbildung 23:
Das MACH – ZEHNDER – Interferometer.............................................................
49
Abbildung 24:
Entstehung von Interferenzstreifen...................................................................
50
Abbildung 25:
Entstehung von Interferenzringen.....................................................................
50
Abbildung 26:
MACH – ZEHNDER – Interferometer als Quantenradierer...................................
53
Abbildung 27:
Aufbau des Interferenzmusters aus den Spuren einzelner Photonen..............
54
Abbildung 28:
Der Quantenradierer als Realexperiment.........................................................
57
Abbildung 29:
Montageplatte...................................................................................................
58
Abbildung 30:
Stangensystem.................................................................................................
58
Abbildung 31:
Umlenkwürfel....................................................................................................
59
Abbildung 32:
Reflexionsvermögen in Abhängigkeit der Wellenlänge....................................
60
Abbildung 33:
Transmissionsvermögen in Abhängigkeit der Wellenlänge..............................
60
Abbildung 34:
Laserdiode........................................................................................................
61
Abbildung 35:
Zentrieraufnahmeplatte.....................................................................................
61
Abbildung 36:
Einklinkbare Aufnahmeplatte............................................................................
62
Abbildung 37:
Aufbau des Quantenradierers...........................................................................
63
137
Abbildung 38:
Aufnahmeplatte.................................................................................................
63
Abbildung 39:
Ringförmiges Interferenzmuster........................................................................
64
Abbildung 40:
Interferenzmuster bei keiner ‚Welcher – Weg’ – Information............................
65
Abbildung 41:
Kein Interferenzmuster bei ‚Welcher – Weg’ – Information...............................
65
Abbildung 42:
Interferenzmuster bei Auslöschung der ‚Welcher – Weg’ – Information...........
66
Abbildung 43:
Experimentelle Anordnung zum Photoeffekt.....................................................
74
Abbildung 44:
Gegenfeldmethode...........................................................................................
76
Abbildung 45:
Versuchsaufbau zum Photoeffekt.....................................................................
77
Abbildung 46:
Frequenzen und Wellenlängen.........................................................................
78
Abbildung 47:
h – Bestimmung durch den Photoeffekt............................................................
80
Abbildung 48:
Versuchsaufbau zum Doppelspalt – Experiment..............................................
80
Abbildung 49:
Bestimmung des Spaltabstands.......................................................................
81
Abbildung 50:
Versuchsaufbau zur Elektronenbeugung..........................................................
83
Abbildung 51:
Schematische Darstellung der Elektronenbeugungsröhre................................
84
Abbildung 52:
Netzebenenabstand von Graphit......................................................................
85
Abbildung 53:
h – Bestimmung durch Elektronenbeugung (kleiner Ring)...............................
88
Abbildung 54:
h – Bestimmung durch Elektronenbeugung (großer Ring)...............................
88
Abbildung 55:
Screenshot aus der Simulation zum Doppelspalt – Experiment.......................
92
Abbildung 56:
Screenshot aus der Simulation zum MACH – ZEHNDER – Intereferometer........
94
Abbildung 57:
Screenshot aus der Simulation zum Bombentest – Experiment.......................
96
Abbildung 58:
Schülergruppe beim Durchführen des Doppelspalt – Experiments von YOUNG
102
Abbildung 59:
Schülergruppe beim Bedienen der Simulation zum Doppelspalt – Experiment
103
Abbildung 60:
Schülergruppe beim Durchführen des Versuchs zum Photoeffekt...................
104
Abbildung 61:
Schülergruppe beim Durchführen des Versuchs zur Elektronenbeugung........
105
Abbildung 62:
Schülergruppe beim Durchführen des Versuchs zum Quantenradierer...........
106
Abbildung 63:
Schülergruppe beim Präsentieren der BOHMschen Mechanik..........................
107
Abbildung 64:
Gesamtbewertung des Schülerlabors...............................................................
109
Abbildung 65:
Bewertung des Schwierigkeitsgrads.................................................................
110
Abbildung 66:
Bewertung der Informativität des Schülerlabors...............................................
111
Abbildung 67:
Bewertung des Interesses an der Physik..........................................................
112
Abbildung 68:
Bewertung der Thematik: ‚Interpretationen der Quantenmechanik’..................
112
138
Tabellenverzeichnis
Tabelle 1:
Messdaten zum Photoeffekt....................................................................................
79
Tabelle 2:
Messdaten zur Elektronenbeugung.........................................................................
86
Tabelle 3:
Messdaten des Kleinen Rings.................................................................................
87
Tabelle 4:
Messdaten des Großen Rings.................................................................................
87
Tabelle 5:
Tagesablauf des Oberstufenkurses aus Hessen....................................................
100
Tabelle 6:
Tagesablauf des Oberstufenkurses aus Rheinland – Pfalz....................................
101
139
Danksagung
An dieser Stelle möchte ich die Gelegenheit nutzen allen, die zum Gelingen dieser
Arbeit beigetragen haben, zu danken.
Mein besonderer Dank gilt Herrn Prof. Dr. Th. Trefzger für die Bereitstellung dieses
interessanten Themas und für eine sehr gute Betreuung.
Prof. Dr. H. – G. Sander möchte ich dafür danken, dass er sich als Korrektor dieser
Arbeit bereiterklärt hat.
Bei K. – H. Geib und Bruno Bauss bedanke ich mich für die Unterstützung und
Hilfsbereitschaft bei der Realisierung des Quantenradierers.
Beiden Lehrern danke ich für die Teilnahme mit ihren Leistungskursen am
Schülerlabor.
Silvia Müller danke ich für ihre Hilfsbereitschaft und Freundlichkeit.
Ein weiterer Dank gilt Alexander Molz, Steman Victor, Marc Saul, Leszek Lupa,
Simon Pockrandt und Benjamin Hinkeldey für eine freundschaftliche und
angenehme Arbeitsatmosphäre.
Bei Alexander Molz, Steman Victor, Florian Goertz und Anke Sperber bedanke ich
mich für ihre Unterstützung und Hilfsbereitschaft bei der Durchführung des
Schülerlabors.
Sabine Schommer möchte ich für ihre moralische Unterstützung und ihre
grenzenlose Geduld danken.
Schließlich möchte ich mich bei meiner Familie bedanken, insbesondere bei
meinen Eltern Georg und Astrid Leuck, die mir dieses Studium ermöglicht haben
und mir jede mögliche Unterstützung haben zukommen lassen.
140
Erklärung
Ich versichere, dass ich meine Staatsexamensarbeit ohne Hilfe Dritter und ohne
Benutzung anderer als der angegebenen Quellen und Hilfsmittel angefertigt und die
den benutzten Quellen wörtlich oder inhaltlich entnommenen Stellen als solche
kenntlich gemacht habe. Diese Arbeit hat in gleicher oder ähnlicher Form noch
keiner Prüfungsbehörde vorgelegen.
Mainz, den 13.09.2007
__________________________
Alexander Leuck
141
Impressum
Alexander Leuck
Ringstrasse 17
66663 Merzig
E-mail: [email protected]
Matrikelnummer: 2524248
Geburtsort: Merzig
Johannes Gutenberg-Universität Mainz
Institut für Physik –ETAP–
Staudinger Weg 7
55099 Mainz
www.physik.uni-mainz.de/lehramt
142