Potential und Spannung

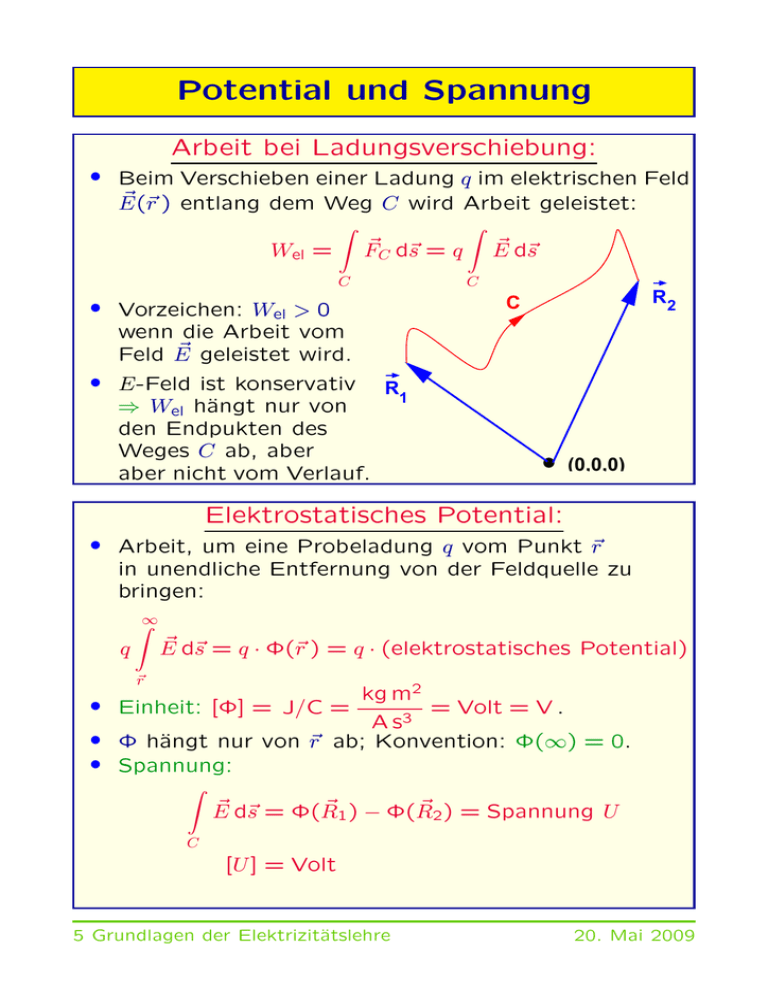
Potential und Spannung
Arbeit bei Ladungsverschiebung:
• Beim Verschieben einer Ladung q im elektrischen Feld
~ r ) entlang dem Weg C wird Arbeit geleistet:
E(~
Z
Z
~ d~s
~C d~s = q E
Wel = F
C
• Vorzeichen: Wel > 0
wenn die Arbeit vom
~ geleistet wird.
Feld E
• E-Feld ist konservativ R
1
⇒ Wel hängt nur von
den Endpukten des
Weges C ab, aber
aber nicht vom Verlauf.
C
R2
C
(0,0,0)
Elektrostatisches Potential:
• Arbeit, um eine Probeladung q vom Punkt ~
r
in unendliche Entfernung von der Feldquelle zu
bringen:
q
Z∞
~ d~s = q · Φ(~
E
r ) = q · (elektrostatisches Potential)
~
r
kg m2
• Einheit: [Φ] = J/C =
= Volt = V .
A s3
• Φ hängt nur von ~
r ab; Konvention: Φ(∞) = 0.
• Spannung:
Z
~ d~s = Φ(R
~ 1 ) − Φ(R
~ 2 ) = Spannung U
E
C
[U ] = Volt
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Potential einer Punktquelle
Berechnung:
• Elektrisches Feld einer Punktladung Q im Ursprung
zeigt radial nach außen.
~ d~s = E dr und damit
• E
Z∞
dr′
Q
Φ(~
r ) = Φ(r) =
4πǫ0
r ′2
∞ r
Q
Q
1
=
=
− ′
4πǫ0
r r
4πǫ0 · r
z
ds
Φ (r)
r
Q>0
Q
y
x
U
R1
R2
r
Q<0
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Beschleunigung im
elektrischen Feld
Potential und Energie:
• Beim Durchlaufen der Spannung U ändert sich die
potentielle Energie eines Teilchens mit Ladung q um
∆Epot = −q · U
• Wegen Energieerhaltung:
∆Ekin = −∆Epot = q · U
• Geladene Teilchen nehmen aus einem elektrischen
Feld kinetische Energie auf, wenn sie es in der
“richtigen” Richtung durchlaufen.
• Beispiele:
– Elektronenstrahl im Fernseher
– Teilchenbeschleuniger
Elektronenvolt:
• Spezielle Energieeinheit für mikroskopische Objekte
(Atome, Kerne, Teilchen):
1 eV = 1 Elektronenvolt = e · 1 V = 1.602 × 10−19 J
• Oft verwendete Vielfache:
1 keV = 103 eV
(Kiloelektronenvolt)
1 MeV = 106 eV
(Megelektronenvolt)
1 GeV = 109 eV
(Gigaelektronenvolt)
• Typische Energieskalen:
– Bindungsenergien in Atomen und Molekülen: eV;
– Röntgenstrahlen: keV;
– Atomkerne: MeV;
– Elementarteilchen: GeV.
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Feld und Potential;
Elektrische Leistung
Feld und Potential:
• Das elektrische Feld kann mit Hilfe der
Definitionsgleichung des elektrostatischen Potentials
aus Φ(~
r ) berechnet werden:
∂Φ
∂Φ
∂Φ
~ r ) = −gradΦ(~
,
,
E(~
r) =
∂x ∂y ∂z
~ r ) zeigt entgegen der Richtung
• Das Feld E(~
r ).
der stärksten Zunahme von Φ(~
~ r ) steht sekrecht auf Flächen mit
• Das Feld E(~
Φ(~
r ) = const. (Äquipotentialflächen).
Elektrische Leistung:
• Elektrische Arbeit beim Transport der Ladung ∆Q
über Spannung U :
∆Wel = ∆Q · U
• Wenn dies in einer Zeit ∆t geschieht (U = const.)
∆Wel
∆Q
= lim
·U =I ·U
∆t→0 ∆t
∆t→0 ∆t
Pel = lim
• Beispiel:
Batterie mit U = 1.5 V und Gesamtladung 1 Ah liefert
Gesamtenergie
Wel = ∆t · I · U = 3600 s · 1 A · 1.5 V = 5.4 kJ
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
Das Ohmsche Gesetz
Strom und Spannung:
• Legt man eine Spannung U an ein Material an, so
fließt im allgemeinen ein Strom I.
• Veranschaulichung im Schaltbild:
Material
(el. Widerstand)
I
Spannungsquelle
+
−
U0
• Für viele Materialien (Metalle, homogene Halbleiter)
gilt bei konstanter Temperatur:
I∝U
⇒
U
= el. Widerstand = const.
I
[R] = V/ A = Ω = Ohm
R=
(Ohm’sches Gesetz)
Strom-Spannungs-Kennlinien:
U
Beispiele
nichtlinearer
Fälle:
U
nicht−linear
Gasentladung
Diode
Glühlampe
linear
(Ohmsch)
I
5 Grundlagen der Elektrizitätslehre
I
20. Mai 2009
Spezifischer Widerstand
Definition:
Der Widerstand eines Drahtes mit Länge L und
Querschnittsfläche A ist
L
1 L
R = ρs · = ·
A
σ A
ρs = spezifischer el. Widerstand
[ρs] = Ωm
σ = spezifische el. Leitfähigkeit
[σ] = Ω−1m−1
L
A
Typische Werte (bei 20◦C):
Material
Kupfer Cu
Eisen Fe
Graphit
Teflon
Hartgummi
spezifischer Widerstand [10−6 Ωm]
0.017
∼ 0.1
∼ 8
1021
1019 . . . 1022
• Der spezifische Widerstand hängt vom Material
(Leitungsmechanismus, mikroskopische Struktur)
und von der Temperatur ab.
• Variiert über fast 30 Größenordnungen!
• Der Wert von ρs in 10−6 Ωm entspricht
dem Widerstand in Ω eines Drahtes mit
Länge L = 1 m und Querschnitt A = 1 mm2.
• Für Metalle (Leitung durch Elektronentransport) sind
elektrische und Wärmeleitfähigkeit proportional.
5 Grundlagen der Elektrizitätslehre
20. Mai 2009
T -Abhängigkeit des Widerstandes
Metalle:
ρs
• Widerstand durch
Stöße der Elektronen
mit Gitteratomen.
• Steigt mit zunehmender
Bewegung der Atome.
• Widerstand nimmt
mit steigender
Temperatur zu.
Halbleiter:
Metall
T
ρs
• Leitung durch Elektronen,
die durch thermische
Energie aus lokaler
Bindung gelöst werden.
• Mit steigendem T nimmt
Zahl der Ladungsträger zu
und Widerstand ab.
• Bei hohen T Widerstandszunahme wie in Metall.
Supraleiter:
• Bei einigen Materialien
wird ρs = 0 bei T < Tc
(Tc : kritische Temperatur,
Sprungtemperatur).
• Quantenmechanischer
Effekt.
• Typisch: Tc (Hg) = 4.183 K;
HochtemperaturSupraleiter: Tc & 100 K .
5 Grundlagen der Elektrizitätslehre
Halbleiter
TRaum
T
ρs
Supraleiter
Tc=einige K
(bei einigen
Stoffen bis
mehrere 10K)
Tc
T
20. Mai 2009
Kirchhoffsche Regeln
Knotenregel:
• Knoten = Kontaktstelle
mehrerer Drähte
ohne aktives Element
• Gesamtladung im Knoten
ist erhalten
⇒
n
X
I1
I2
Ii = 0
I3
i=1
• Vorzeichen geben
Richtung der Ströme!
• Knotenregel bzw.
1. Kirchhoffsche Regel
I4
Knoten
U1
Maschenregel:
• Masche = Leitungskreis
mit Spannungsquelle(n)
und Widerstände(n).
~ s
• Wegintegral von Ed~
entlang Masche verschwindet
n
X
i=0
Ui = I
n
X
i=1
R1
U0 +
−
I
I
Ri − |U0| = 0
• Spannungen von Quelle
und an Widerständen
haben entgegengesetzte
Vorzeichen.
• Maschenregel bzw.
2. Kirchhoffsche Regel
5 Grundlagen der Elektrizitätslehre
R2
U2
20. Mai 2009