Die Keplerschen Gesetze

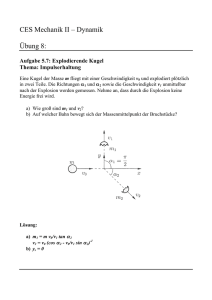
Die Keplerschen Gesetze
===================================================================
1. Galileische Monde
a)
TIo2
TCa2
=
aIo3
aCa3
⇒

3
6
4,218
⋅
10
km

 = 55,91 d
 1,884 ⋅ 106 km 


TIo = 16,69 d ⋅
3
b)aEu = aCa ⋅
TIo = TCa⋅
 a 3
 Io 
 aCa 


 T 2
 Eu 
 TCa 


3
6
aEu = 1,884⋅10 km ⋅
 3,55 d 2
6

 ≈ 0,6713⋅10 km
16,69
d


 T 2
3
Ga 

aGa = aEu ⋅ 22 = 1,59⋅aEu
c) aGa = aEu ⋅
 TEu 


-------------------------------------------------------------------------------------------------------------2. Gegeben:
3
große Halbachse bzw. mittlerer Abstand
1 AE
Erde
Ceres
Umlaufsdauer
365 d
1682 d
Gesucht: aCeres
3
 1682 d 2

 = 2,77 AE
 365 d 
___________________________________________________________________________
aCeres = aErde ⋅
Die Newtonschen Gesetze
===================================================================
1. Wenn ruckartig angefahren wird, dann wird der abgeschleppte Wagen stark beschleunigt.
Nach actio = reactio zieht der abgeschleppte Wagen dann mit einer großen Kraft am Seil.
-------------------------------------------------------------------------------------------------------------m
m
2. Gegeben: m = 250 kg und M = 900 kg sowie ∆ = 1,6 s → 0
→ 1,5
s
s
∆v
Beschleunigung: a =
∆t
Bewegung nach oben:
1,5 ms
m
a =
= 0,94 2
1,6 s
s
FS = (m + M)⋅(a + g) FS = 1,16 kN
Bewegung nach unten:
FS = (m + M)⋅(g − a) Fs = 10,2 kN
-------------------------------------------------------------------------------------------------------------3. Gegeben: m = 1,2 t und tanα = 0,15
x = 100 m
→
v = 15
⇒
α = tan−1(0,15) = 9,5°
m
s
Gesucht: Motorkraft FM
Beschleunigende Kraft: F = FM − FH
Zweites Newtonsches Gesetz: FM − FH = m⋅a
2
⇒
Berechnung von a: v = 2ax
v2
a =
2x
⇒
a =
FM = FH + m⋅a = m⋅g⋅sinα + m⋅a
(15
m 2
s )
2⋅ 100 m
= 1,125
m
s2


m
m

Eingesetzt: FM = 1200 kg⋅ 9,81 2 ⋅sin9,5° + 1,125 2 = 3,1 kN

s
s 


-------------------------------------------------------------------------------------------------------------1
4. Gegeben: m1 = 1 kg und a =
g
10
a) Gesucht: m2
Beschleunigende Kraft: F = m2⋅g − m1⋅g
Beschleunigte Masse: m = m1 + m2
Zweites Newtonsches Gesetz: m2⋅g − m1⋅g = (m1 + m2)⋅a = (m1 + m2)⋅
⇒
9
11
g⋅m2 =
g⋅m1
10
10
⇒ m2 =
1
g
10
11
m = 1,2 kg
9 1
b) Gesucht: t für s = 1m
s =
1 2
a⋅t
2
⇒
t =
2s
a
t =
2m
0,1 ⋅ 9,81
m
s2
= 1,4 s
--------------------------------------------------------------------------------------------------------------
5. Gegeben: m = 1060 kg und v = 72
km
m
= 20
sowie FW = 0,05⋅G
h
s
a) Gesucht: FM
Für eine Bewegung mit konstanter Geschwindigkeit muss die Summe aller angreifenden
Kräfte gleich Null sein.
Also FM = FW
FM = 0,05⋅1060 kg⋅9,81
m
= 0,52 kN
s2
20 ms
∆v
m
=
= 1,67 2
b) Gesucht: FM, wenn a =
12
s
∆t
s
m
= 2,3 kN
s2
-------------------------------------------------------------------------------------------------------------Aufgabe schwierig! Versehentlich in das Übungsblatt aufgenommen!
FM − FW = m⋅a
⇒
FM = FW + m⋅a
FM = 520 N + 1060 kg⋅1,67
Für Interessierte
Problemanalyse
1. Beide Körper bewegen sich nicht mit der gleichen Beschleunigung. Der Körper am Flaschenzug bewegt sich nur mit der halben Beschleunigung wie der auf der schiefen Ebene.
2. Die lose Rolle muss berücksichtigt werden.
Es empfiehlt sich die Methode der isolierten Körper d.h. man betrachtet die Körper
unabhängig voneinander.
6. Gegeben: m = 300 g und M = 700 g sowie l = 5,00 m und h = 3,00 m
Also tanα =
3
5
⇒
α = 34,4°
Gesucht: a
Anwendung des zweiten Newtonschen Gesetzes auf die beiden Körper
(1) M⋅g − 2⋅T = M⋅
a
2
(2) T − FH = m⋅a
Dabei ist T die Kraft, die das Seil auf den Körper auf der schiefen Ebene ausübt.
Aus (2) folgt: T = FH + m⋅a
In (1) : M⋅g − 2⋅(FH + m⋅a) = M⋅
M⋅g − 2FH
a
2
⇔
M⋅g − 2FH = M⋅
a
+ 2⋅ma
2
0,7 kg ⋅ 9,81 m2 − 2⋅0,3 kg ⋅9,81 m2 ⋅sin34,4°
m
0,35 kg + 0,6 kg
s2
___________________________________________________________________________
a =
1
2 M + 2m
a =
s
s
= 4,0
Energieerhaltung
==================================================================
=
1. Gegeben: m = 0,20 kg und v = 20
m
sowie h = 5,0 m
s
Gesucht: v1
1
1
m⋅v2 = mg⋅h + m⋅v12
2
2
⇒ v1 =
v2 − 2g⋅h
m 2
m
m
) − 2 ⋅ 9,81 2 ⋅ 5 m = 17,3
s
s
s
-------------------------------------------------------------------------------------------------------------N
2. Gegeben: m = 1,2 kg, h = 0,40 m und D = 0,5
m
v1 =
(20
Gesucht: v
mg⋅h =
1
1
D⋅h2 + m⋅v2
2
2
⇒
v =
2mg⋅h − D⋅h2
m
N
m
⋅ 0,2 m − 0,5
⋅(0,4 m)2 = 2,2
2
m
s
s
___________________________________________________________________________
v =
2 ⋅ 1,2 kg ⋅ 9,81
Impulserhaltung
==================================================================
=
km
km
1. Gegeben: m1 = 15 t und v1 = 8,0
sowie m2 = 18 t und v21 = 3,0
h
h
Gesucht: u
Impulserhaltung:
m1⋅v1 + m2⋅v2 = (m1 + m2)⋅u
⇒
u =
m1⋅v1 + m2⋅v2
m1 + m2
km
h
15 t ⋅ 8
+ 18 t ⋅ 3
km
h
km
h
15 t + 18 t
-------------------------------------------------------------------------------------------------------------u =
= 5,3
2. Gegeben: m = 2 kg und v1 = 8
u1 = − 4
m
m
sowie v2 = 0
s
s
m
m
und u2 = 4
s
s
Impulserhaltung:
m1⋅v1 = m1⋅u1 + m2⋅u2
m2 =
2 kg ⋅ 8
m
s
⇒ m2 =
− 2 kg ⋅ ( − 4
4
m
s )
m
s
m1⋅v1 − m1⋅u1
u2
= 6 kg
Die Aufgabe lässt sich auch mit dem Energiererhaltungssatz lösen!
-------------------------------------------------------------------------------------------------------------3. Gegeben: v2 = − v1 = − v und u2 = 0
Energieerhaltung:
1
1
1
m1⋅v2 + m2⋅v2 = m1⋅u2
2
2
2
⇔
(m1 + m2)⋅v2 = m1⋅u2
Impulserhaltung:
m1⋅v − m2⋅v = m1⋅u
⇒
u =
m1⋅v − m2⋅v
m1 − m2
=
⋅v
m1
m1
Eingesetzt:
 m − m 2
1
2 
(m1 + m2)⋅v = m1⋅
⋅v
 m1



2
m12 + m1m2 = m12 − 2m1m2 + m22
⇒
⇔
(m1 − m2)2
m1 + m2 =
m1
0 = − 3m1m2 + m22
⇒ m2 = 3m1
Die Masse der Kugel, die nach dem Stoß ruht, muss dreimal so groß wie die Masse der anderen Kugel sein.
(m1 + 3m1)⋅v2 = m1⋅u2
⇒ u2 = 4v2
⇒ u = − 2v
Die erste Kugel bewegt sich dann mit doppelter Geschwindigkeit in die andere Richtung.
-------------------------------------------------------------------------------------------------------------km
m
4. a) Gegeben: m1 = 60 kg und v1 = 18
= 5
sowie
h
s
m2 = 80 kg und v2 = 5,4
km
m
= 1,5
h
s
Gesucht: u
Impulserhaltung: m1⋅v1 + m2⋅v2 = (m1 + m2)⋅u ⇒
u =
m
s
60 kg ⋅ 5
m
s
+ 80 kg ⋅ 1,5
60 kg + 80 kg
= 3
u =
m
s
60 kg ⋅ 5
m1⋅v1 + m2⋅v2
m1 + m2
m
s
Der Wagen bewegt sich mit Peter zusammen mit 3
b) Gesucht: u, wenn v2 = − 1,5
u =
m
in die Laufrichtung von Peter.
s
m
s
+ 80 kg ⋅ ( − 1,5
m
s )
60 kg + 80 kg
= 1,3
m
s
m
in die Laufrichtung von Peter.
s
-------------------------------------------------------------------------------------------------------------m
5. Gegeben: m1 = 600 kg und v1 = 2,5
sowie m2 = 400 kg
s
Der Wagen bewegt sich mit 1,3
Gesucht: u
Impulserhaltung:
m1⋅v1 = (m1 + m2)⋅u
⇒ u =
m1⋅v1
m1 + m2
u =
600 kg ⋅ 2,5
m
s
600 kg + 400 kg
= 1,5
m
s
m
weiter.
s
___________________________________________________________________________
Die Lore bewegt sich mit 1,5